文章信息
- 李忠奇, 陶必林, 占梦瑶, 吴祝超, 吴继周, 王建明.
- Li Zhongqi, Tao Bilin, Zhan Mengyao, Wu Zhuchao, Wu Jizhou, Wang Jianming
- 时间序列模型应用于新型冠状病毒肺炎疫情预测效果比较研究
- A comparative study of time series models in predicting COVID-19 cases
- 中华流行病学杂志, 2021, 42(3): 421-426
- Chinese Journal of Epidemiology, 2021, 42(3): 421-426
- http://dx.doi.org/10.3760/cma.j.cn112338-20201116-01333
-
文章历史
收稿日期: 2020-11-16
2019年年末新发现的新型冠状病毒肺炎(COVID-19)已造成全球大流行,成为影响人类健康的重大公共卫生问题[1]。准确预测COVID-19的发病趋势可以帮助政府部门合理分配医疗卫生资源,及时调整防控策略,有效遏制疫情。时间序列分析是根据系统观测获得的数据,通过曲线拟合和参数估计来建立数学模型的一类方法。差分自回归移动平均(autoregressive integrated moving average,ARIMA)模型和循环神经网络(recurrent neural network,RNN)模型是两种常见的时间序列模型。其中,ARIMA模型已被用于预测意大利、西班牙和法国等国家的COVID-19疫情,并被证明具有良好的预测性能[2],但尚未有研究探索应用RNN模型预测COVID-19并比较其预测能力。因此,本研究通过构建ARIMA模型和RNN模型,旨在比较这两种模型应用于预测不同地区COVID-19疫情的表现。
资料与方法1. 数据收集:据WHO统计数据,截至2020年9月30日,美国、印度和巴西分别确诊7 077 015、6 225 763和4 745 464例COVID-19,是全球累计确诊病例数最多的3个国家[1]。因此,从WHO发布COVID-19疫情数据的网站(https://covid19.who.int/)收集上述3个国家2020年4月1日至9月30日期间每日确诊病例数,用于构建时间序列模型并评估其预测性能。
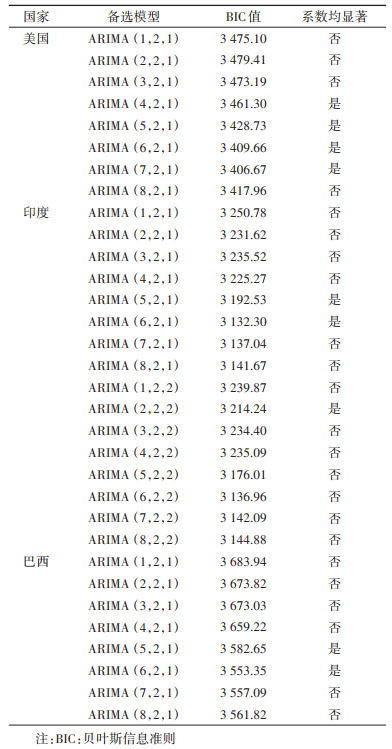
2. ARIMA模型的构建:ARIMA模型是最经典、最成熟的时间序列模型,该模型对数据的分布类型不做特殊要求,已被广泛应用于结核病[3]、手足口病[4]和乙型肝炎[5]等传染病的预测。ARIMA模型可以表示为ARIMA(p,d,q),其中p表示自回归的阶数,d表示差分的次数,q表示移动平均的阶数。构建ARIMA模型包含4个步骤:①通过时间序列图和单位根检验判断序列是否平稳,若不平稳,则通过差分的方式使其平稳;②根据平稳序列的自相关系数图和偏自相关系数图初步确定p和q的取值,以构建一些备选模型,其中p的取值参考偏自相关系数图,q的取值参考自相关系数图;③根据最小化贝叶斯信息准则(Bayesian information criterion,BIC)值的原则确定最佳模型;④对模型的系数进行假设检验并检测其残差是否为白噪声,如果模型的某项系数不显著或其残差被证明为非白噪声,则应重新选择模型[6]。确定最佳ARIMA模型后,用其预测9月21-30日的COVID-19确诊病例数。
3. RNN模型的构建:ARIMA模型本质上是一种线性回归模型,考虑到COVID-19的发病趋势可能是非线性,因此,构建了另一种非线性模型,即RNN模型。RNN模型是一种常见的神经网络模型,除了具有强大的非线性拟合能力外,还拥有记忆功能。神经网络模型通常由输入层、隐藏层和输出层组成,传统的神经网络模型层与层之间完全连接,但每一层中的神经元彼此之间没有连接,而RNN模型则在隐藏层的神经元间添加连接,其隐藏层的输入不仅包括输入层的输出,还包括隐藏层先前的输出,从而使其具有跨时间步长传递信息的能力,特别适合用于时间序列分析[7-8]。本研究将2020年4月1日至9月30日的每日确诊数据划分为训练集、测试集和预测集,共构建了10个RNN模型(RNN1~RNN10),RNN1使用前1天的数据预测当日的数据,RNN2使用前2天的数据预测当日的数据,以此类推。在训练前对数据进行归一化处理,使用公式: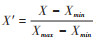
4. 模型预测性能比较:采用平均绝对百分比误差(mean absolute percentage error,MAPE)和均方根误差(root mean square error,RMSE)比较模型的预测性能[9-10]。
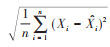
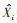
5. 统计学分析:使用R 4.0.2中的“forecast”“tseries”和“rnn”包构建ARIMA和RNN模型,检验水平α=0.05,以P < 0.05为差异有统计学意义。
结果1. ARIMA模型:2020年4月1日至9月20日,美国、巴西和印度的COVID-19每日确诊病例数见图 1。美国和巴西的日确诊病例数在7月底和8月初达到峰值,而后略有下降,而印度的日确诊病例数则一直波动性上升,未出现明显的下降趋势。
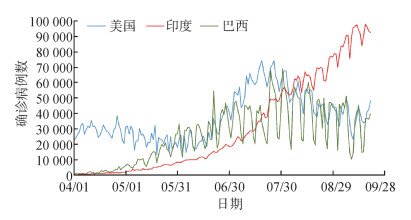
|
| 图 1 美国、印度和巴西2020年4月1日至9月20日的每日确诊病例数 |
对病例序列进行两次差分后经单位根检验,结果显示,序列已经平稳(P < 0.01)。平稳序列的自相关系数和偏自相关系数见图 2 A1~A3和B1~B3。对于美国和巴西,初步确定p=1~8,q=1;对于印度,初步确定p=1~8,q=1~2,最终确定ARIMA(6,2,1)为最优ARIMA模型。对于美国,尽管ARIMA(6,2,1)的BIC值略大于ARIMA(7,2,1),但考虑到模型复杂度和p的取值较高可能会导致过拟合问题,因此,仍选择ARIMA(6,2,1)为美国的最优ARIMA模型(表 1)。参数假设检验显示,模型各项系数均有统计学意义(P < 0.05),其残差序列的自相关性和偏自相关性已经基本消除,可认为其为白噪声序列(图 2 C1~C3和D1~D3)。

|
| 注:A:平稳序列的自相关系数图;B:平稳序列的偏自相关系数图;C:ARIMA模型残差的自相关系数图;D:ARIMA模型残差的偏自相关系数图;1:美国;2:印度;3:巴西 图 2 自相关系数图和偏自相关系数图 |
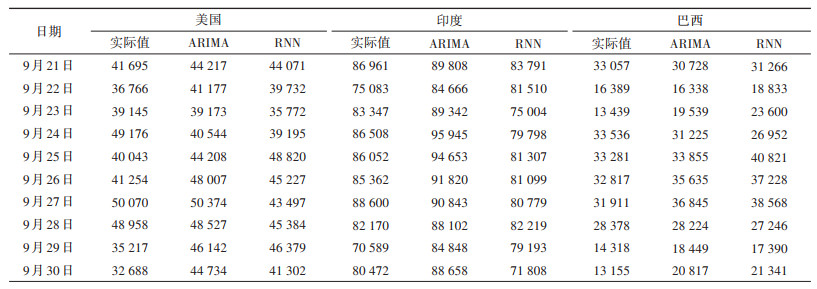
使用ARIMA(6,2,1)预测3个国家9月21- 30日的确诊病例数,结果见表 2。
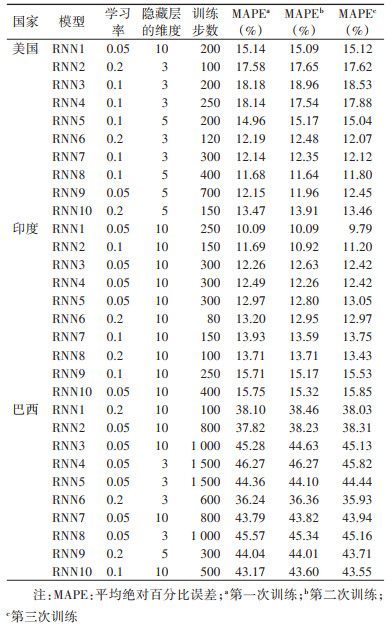
2. RNN模型:比较3个国家不同RNN模型在测试集上的表现,结果见表 3。最终确定RNN8、RNN1和RNN6分别为美国、印度和巴西的最优RNN模型,其在测试集上的MAPE值较小。考虑在3次训练中最小的测试集MAPE值,因此,选择第二次训练后的RNN8、第三次训练后的RNN1和RNN6分别预测美国、印度和巴西9月21-30日的确诊病例数,结果见表 2。
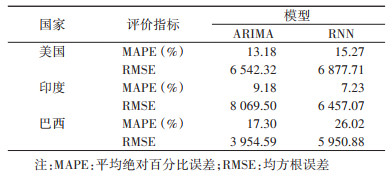
3. 模型预测性能比较:使用两种模型分别预测3个国家9月21-30日共计10 d的病例数,发现模型的预测性能在不同国家存在差异。在美国,ARIMA模型有6 d优于RNN模型;在印度,RNN模型有6 d优于ARIMA模型;在巴西,ARIMA模型有8 d优于RNN模型。随后,使用MAPE和RMSE两个指标比较两个模型在预测集上的总体表现(表 4)。结果显示,ARIMA模型在美国和巴西的MAPE和RMSE值较小,而RNN模型在印度的MAPE和RMSE值较小。因此,总体而言,ARIMA模型在美国和巴西的表现要优于RNN模型,而RNN模型在印度的表现要优于ARIMA模型。
构建合适的预测模型能够为政府合理配置医疗卫生资源和制定疾病防控策略提供参考。COVID-19疫情发生后,已有研究者采用时间序列模型来预测新发病例的变化趋势[2, 11-12],但是,较少有研究比较不同模型在不同地区的预测效果。本研究构建了两种不同的时间序列模型,并在全球累计确诊病例数最多的3个国家(美国、印度和巴西)进行评估,结果发现,ARIMA模型预测的准确性在美国和巴西较高,而RNN模型预测的准确性在印度较高。
ARIMA模型具有构建相对简单、对数据分布类型没有特殊要求的特点,是使用最为广泛的时间序列模型。例如,Liu等[13]使用ARIMA(0,3,1)模型来预测2009-2011年中国肾综合征出血热的发病率,Moosazadeh等[14]构建SARIMA(0,1,1)(0,1,1)12模型预测伊朗2015年涂阳结核病的发病率。COVID-19疫情发生以来,一些学者使用传染病动力学模型来预测其流行趋势[15-17]。然而,这些动力学模型的构建过程比较复杂,需要考虑较多的因素,使用者需要具备较深的专业知识。因此,一些研究者开始尝试使用ARIMA模型来预测COVID-19的流行情况[2, 11-12]。本研究确定ARIMA(6,2,1)为美国、印度和巴西的最优ARIMA模型,该模型用于预测3个国家9月21-30日确诊病例数时的MAPE均 < 20%,具有较高的准确性。
尽管ARIMA模型在预测COVID-19时具有良好的表现,但是,考虑到COVID-19的发生往往受到多种因素的综合作用,如医疗卫生资源的配给、防控措施的实施和环境变化等,其发病趋势可能呈现出非线性特征。而RNN模型则可以弥补ARIMA模型只能处理线性特征的不足,该模型除了具有普通神经网络强大的非线性拟合能力外,还拥有记忆功能,不仅使用当前数据作为输入信息,还可利用其长期经验[18]。由于训练集的构成会影响神经网络模型的预测性能,因此本研究分别使用前1天至前10天的数据作为训练集的输入,使用当日的数据作为训练集的输出,共构建了10个不同的RNN模型。考虑到RNN模型的构建需要人工设置一些参数,如学习率、隐藏层的维度和训练步数等,且在训练时其初始权重和阈值是随机分配的,即使训练集相同,其测试集的输出也不会完全相同,所以对具有不同参数组合的RNN模型进行了3次训练,通过比较其在测试集上的表现确定最佳的RNN模型。
通过比较研究,ARIMA模型的预测性能在美国和巴西要优于RNN模型,而RNN模型的预测性能在印度要优于ARIMA模型。这种差异可能归因于两个原因,一是不同地区的发病趋势可能存在差异,二是两种模型建立时未考虑干预措施、诊断手段和报告质量等因素的影响。因此,在预测COVID-19疫情时,需针对不同地区的特点应选择不同的最优模型。
本研究存在局限性。首先,我们仅评估了两种模型预测COVID-19的表现,其他种类的时间序列模型,如灰色模型和指数平滑模型等未被考虑。其次,无论是ARIMA模型还是RNN模型,本质上都属于短期预测模型,无法预测其长期趋势,因此需要不断地收集和更新数据以保证其预测性能。第三,本研究使用的COVID-19发病数据来源于WHO官方公布的结果,与各国实际的发病数据可能存在一定的差异。第四,相比传染病动力学模型等其他预测模型,时间序列模型无法体现干预措施、诊断手段和报告质量等因素对疫情的影响。最后,COVID-19具有冬春季高发的特点,本研究仅收集了2020年4月1日至9月30日的病例数据,无法体现其病例分布的周期性和季节性。
利益冲突 所有作者均声明不存在利益冲突
| [1] |
World Health Organization. WHO Coronavirus Disease (COVID-19) Dashboard[EB/OL].[2020-11-09]. https://covid19.who.int/.
|
| [2] |
Ceylan Z. Estimation of COVID-19 prevalence in Italy, Spain, and France[J]. Sci Total Environ, 2020, 729: 138817. DOI:10.1016/j.scitotenv.2020.138817 |
| [3] |
Li ZQ, Wang ZZ, Song H, et al. Application of a hybrid model in predicting the incidence of tuberculosis in a Chinese population[J]. Infect Drug Resist, 2019, 2019, 12: 1011-1020. DOI:10.2147/idr.s190418 |
| [4] |
Liu WD, Bao CJ, Zhou YP, et al. Forecasting incidence of hand, foot and mouth disease using BP neural networks in Jiangsu province, China[J]. BMC Infect Dis, 2019, 19: 828. DOI:10.1186/s12879-019-4457-6 |
| [5] |
Zheng YL, Zhang LP, Zhu XX, et al. A comparative study of two methods to predict the incidence of hepatitis B in Guangxi, China[J]. PLoS One, 2020, 15(6): e0234660. DOI:10.1371/journal.pone.0234660 |
| [6] |
Liu Q, Li ZQ, Ji Y, et al. Forecasting the seasonality and trend of pulmonary tuberculosis in Jiangsu Province of China using advanced statistical time-series analyses[J]. Infect Drug Resist, 2019, 12: 2311-2322. DOI:10.2147/idr.s207809 |
| [7] |
Chen YY, Cheng QQ, Cheng YJ, et al. Applications of recurrent neural networks in environmental factor forecasting: a review[J]. Neural Comput, 2018, 30(11): 2855-2881. DOI:10.1162/neco_a_01134 |
| [8] |
Kim ZM, Oh H, Kim HG, et al. Modeling long-term human activeness using recurrent neural networks for biometric data[J]. BMC Med Inform Decis Mak, 2017, 17: Suppl 1-57. DOI:10.1186/s12911-017-0453-1 |
| [9] |
Wang YW, Shen ZZ, Jiang Y. Comparison of ARIMA and GM(1, 1) models for prediction of hepatitis B in China[J]. PLoS One, 2018, 13(9): e0201987. DOI:10.1371/journal.pone.0201987 |
| [10] |
Akinbobola A, Omotosho JB. Predicting malaria occurrence in southwest and north central Nigeria using meteorological parameters[J]. Int J Biometeorol, 2013, 57(5): 721-728. DOI:10.1007/s00484-012-0599-6 |
| [11] |
Ilie OD, Cojocariu RO, Ciobica A, et al. Forecasting the spreading of COVID-19 across nine countries from Europe, Asia, and the American continents using the ARIMA models[J]. Microorganisms, 2020, 8(8): 1158. DOI:10.3390/microorganisms8081158 |
| [12] |
Malki Z, Atlam ES, Ewis A, et al. ARIMA models for predicting the end of COVID-19 pandemic and the risk of second rebound[J/OL]. Neural Comput Appl, 2020. DOI: 10.1007/s00521-020-05434-0.
|
| [13] |
Liu QY, Liu XD, Jiang BF, et al. Forecasting incidence of hemorrhagic fever with renal syndrome in China using ARIMA model[J]. BMC Infect Dis, 2011, 11: 218. DOI:10.1186/1471-2334-11-218 |
| [14] |
Moosazadeh M, Khanjani N, Nasehi M, et al. Predicting the incidence of smear positive tuberculosis cases in Iran using time series analysis[J]. Iran J Public Health, 2015, 44(11): 1526-1534. |
| [15] |
Wang K, Ding L, Yan Y, et al. Modelling the initial epidemic trends of COVID-19 in Italy, Spain, Germany, and France[J]. PLoS One, 2020, 15(11): e0241743. DOI:10.1371/journal.pone.0241743 |
| [16] |
IHME COVID-19 Forecasting Team. Modeling COVID-19 scenarios for the United States[J/OL]. Nat Med, 2020. DOI: 10.1038/s41591-020-1132-9.
|
| [17] |
刘雅姝, 吴琪俊, 陆一涵, 等. 新型冠状病毒肺炎(COVID-19)传染病预测模型分析[J]. 公共卫生与预防医学, 2020, 31(3): 10-13. Liu YS, Wu QJ, Lu YH, et al. Analysis of models of infectious disease dynamics of COVID-19[J]. J Public Health Prev Med, 2020, 31(3): 10-13. DOI:10.3969/j.issn.1006-2483.2020.03.003 |
| [18] |
Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
 2021, Vol. 42
2021, Vol. 42