文章信息
- 洪航, 史宏博, 姜海波, 顾晓敏, 陈奕, 丁克琴, 许国章.
- Hong Hang, Shi Hongbo, Jiang Haibo, Gu Xiaomin, Chen Yi, Ding Keqin, Xu Guozhang
- 基于传染病动力学模型的宁波市新型冠状病毒肺炎防控措施效果评估
- Epidemic dynamic model based evaluation of effectiveness of prevention and control strategies for COVID-19 in Ningbo
- 中华流行病学杂志, 2020, 41(10): 1606-1610
- Chinese Journal of Epidemiology, 2020, 41(10): 1606-1610
- http://dx.doi.org/10.3760/cma.j.cn112338-20200311-00313
-
文章历史
收稿日期: 2020-03-11
新型冠状病毒肺炎(COVID-19)是由新型冠状病毒感染引起的一种新型急性呼吸道传染病[1-2],我国将其纳入《中华人民共和国传染病防治法》规定的乙类传染病,按甲类传染病管理[3]。宁波市首例COVID-19病例自1月14日发病以来,政府出台了一系列防控措施,有效遏制了疫情的快速蔓延。但是,当前世界各地疫情仍然比较严峻[4-6]。本研究基于SEIR[易感人群(susceptible,S);潜伏期人群(exposed,E);感染者(infectious,I);恢复人群(recovered,R)]传播动力学模型[7],结合宁波市疫情变化特征和防控措施落实情况,综合评估防控措施落实对于疫情控制的成效。
材料与方法1.数据来源:宁波市2020年COVID-19疫情个案数据来源于“中国疾病预防控制信息系统”、“突发公共卫生事件报告信息系统”和宁波市卫生健康委官方网站报告。同期人口数据来源于宁波市统计年鉴。
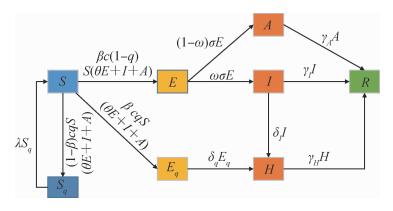
2.传播动力学模型:根据宁波市COVID-19疫情个案数据、疾病进程、严格的防控措施(对易感者、潜伏期人群医学观察、感染者隔离治疗等)等数据,在传统SEIR模型的基础上,增加被隔离的易感人群(Sq)和被隔离的潜伏期人群(Eq),建立SEIR-QAH[隔离人群(quarantined,Q);无症状感染者(asymptomatic infectious,A);住院者(hospitalized,H)]动力学模型,见图 1。具体微分方程见公式(1)。
|
| 注:S:易感人群; E:潜伏期人群; I:感染者; R:恢复人群; Sq:被隔离的易感人群; Eq:被隔离的潜伏期人群; Q:隔离人群; A:无症状感染者; H:住院者 图 1 宁波市严格管控措施下COVID-19传播动力学模型示意图 |
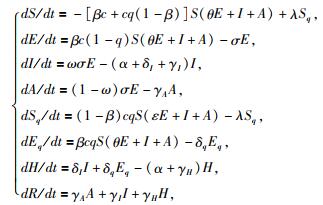 (1)
(1)
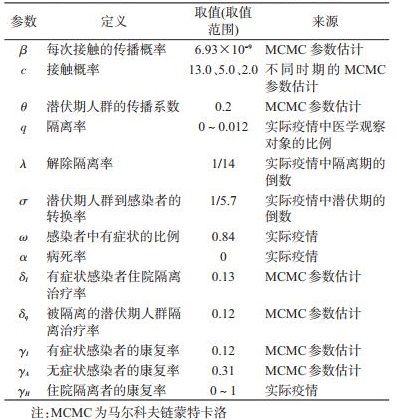
3.参数估计:本模型中接触后隔离率q(实际疫情中医学观察人群的比例)、隔离解除的比例λ(实际疫情中隔离期的倒数)、潜伏期人群到感染者人群的转换率σ(实际疫情中潜伏期的倒数)、有症状感染者的比例ω、病死率α、隔离治疗者的康复率γH等参数主要通过实际疫情的数据获得。易感人群每次接触感染者的传播概率β,每次接触潜伏期人群相对于接触感染者的传播概率的比例θ,接触概率c,感染者隔离治疗率δI,被隔离的潜伏期人群隔离治疗率δq,有症状感染者康复率γI、无症状感染者的康复率γA等参数通过马尔科夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)的Metropolis-Hastings(M-H)算法拟合模型估计。模型预测的起始时间为1月14日。为评估一级响应后采取管控措施对疫情的影响,固定其他参数,估计1月23日后接触概率为5.0、2月4日后接触概率为2.0。具体参数设置见表 1。利用再生矩阵的方法估计基本再生数(R0)和实时再生数(Rt),Rt计算见公式(2)。
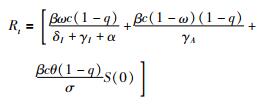 (2)
(2)
4.统计学分析:采用Excel 2013和SPSS 21.0软件对数据进行统计描述和作图,按照病例发病时间整理宁波市疫情数据,并绘制流行曲线图。采用Matlab Version 2019b软件将整理好的宁波市疫情数据作为模型数据库,构建SEIR-QAH模型。基于动力学模型进行参数估计、预测不同接触概率下的新增病例数及估计R0和Rt。
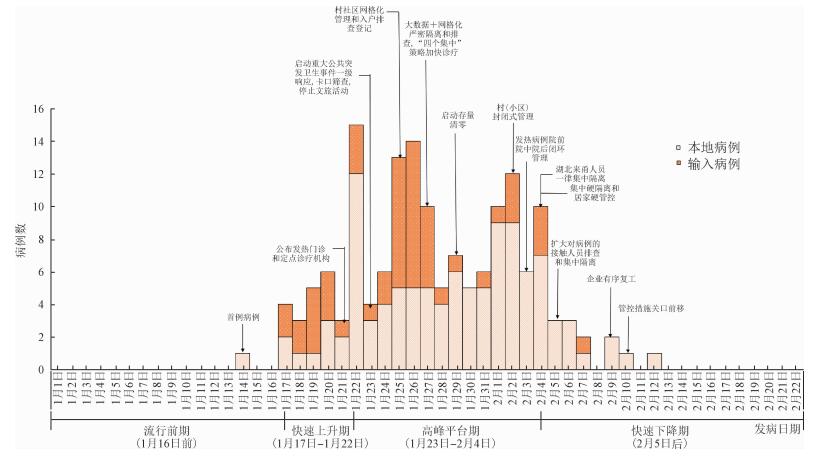
结果1.流行病学特征及防控措施:截至2020年3月9日24:00,宁波市累计报告COVID-19确诊病例157例,累计报告发病率为1.8/10万。所有病例均已出院,无死亡病例。其中重症病例19例、占总病例数的12.1%。共报告输入性病例51例、本地病例106例。共发现无症状感染者30例。流行曲线共分为4期:1月16日前为流行前期,其中首例病例发病日期为1月14日;快速上升期共6 d(1月17-22日);高峰平台期共13 d(1月23日至2月4日),其中有2次高峰;2月5日后进入快速下降期,2月12日后无新增病例(图 2)。
|
| 图 2 宁波市COVID-19确诊病例流行曲线 |
宁波市于1月23日启动重大公共突发卫生事件一级响应,采取了延迟复工复学、卡口筛查、村(小区)封闭管理等一系列措施。特别是2月3日实施发热病例闭环管理,提高了病例的“早发现”能力。2月4日,对湖北省来甬(宁波)人员一律集中硬隔离,对居家观察采取大门贴封条、安装摄像头、手机轨迹定位等硬管控措施。2月5日,针对1月19日一起佛事集会引起的聚集性疫情(28人确诊),扩大对该起疫情1例“超级传播者”的接触人员排查。对所有密切接触者以及密切接触者的接触人员采取集中隔离医学观察措施,使得新增病例数快速下降,病例发病周期控制在1个月以内。
2.疾病进程和潜伏期:157例确诊病例中,发病到第一次就诊的时间最短为0.5 d,最长为11 d,M为0.5 d,QR为1.5 d。从发病到确诊的时间最短为1 d,最长为17 d,平均(5.4±3.7)d。155例出院病例中,从确诊到出院的时间最短为4 d,最长为35 d,平均(16.6±6.5)d。58例暴露时间明确的病例中,从暴露到发病(潜伏期)的时间最短为2 d,最长为15 d,平均(5.7±2.9)d。
3.医学观察情况:截至2020年3月9日24:00,累计医学观察105 339人,医学观察的对象除了密切接触者外,还包括所有高、中风险地区(确诊病例数>100例的地级市)来甬人员、发热病例、佛事聚集性疫情中密切接触者的接触人员等。其中,集中医学观察15 440人,居家医学观察89 899人。医学观察者中发现确诊病例共99例(63.1%)。集中医学观察者中,共有确诊病例45例,病例发现率为0.3%;居家医学观察者中,共有确诊病例54例,病例发现率为0.1%。
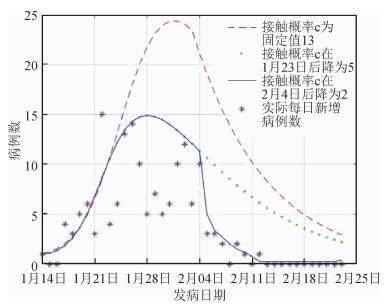
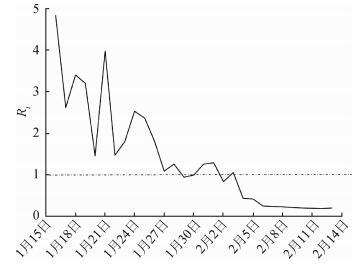
4.传播动力学分析:根据流行病学资料(潜伏期、隔离期、有症状感染者的比例、医学观察人群的比例、病死率)和方程确定相关参数,建立SEIR- QAH模型。为分析1月23日启动一级响应后防控措施对疫情的影响,接触概率c分别取固定值和分阶段值的情况下预测病例数和实际每日新增病例数。见图 3。假设接触概率c取固定值13.0,每日新增病例峰值可能会达到2月1日的25例;假设c从1月14日的13.0降到1月23日的5.0,峰值提前到1月27日的15例,之后缓慢下降;假设c从1月23日的5.0降到2月4日的2.0,2月4日后疫情快速下降。根据模型结果拟合宁波市在流行前期(实施防控措施前)R0为4.8。随着防控措施的加强,Rt呈逐渐下降趋势。特别是2月4日后,通过采取加大密切接触者排查和加强隔离医学观察措施,Rt下降至1.0以下,之后持续下降到2月中旬的0.2(图 4)。
|
| 图 3 COVID-19传播动力学模型预测宁波市不同接触概率情况下的新增病例数和实际新增病例数比较 |
|
| 图 4 宁波市COVID-19基本再生数的变化趋势 |
根据宁波市COVID-19流行曲线特征描述来看,疫情总体呈现暴发流行趋势[6]。疫情于1月17日进入快速上升期,23日起进入高峰平台期,2月5日进入快速下降期,13日后无新增确诊病例。以本地病例为主,具有聚集性发病的流行病学特点,高峰平台期持续时间较长。因此,在防控过程中减少聚集性疫情的发生,控制社区传播有助于控制疫情的传播与扩散[8]。
在COVID-19防控期间,宁波市制定并出台了一系列疫情防控措施。主要包括:延迟复工复学、卡口筛查、村(小区)封闭管理、网格化排查、判定重点地区、扩大密切接触者排查、实施严格的医学隔离措施、发热病例全周期闭环管理等。一方面加快疾病诊断,隔离诊治传染源。另一方面规范密切接触者管理,重视聚集性疫情防控,缩短了发病到就诊时间。根据估计的潜伏期(5.7±2.9)d,和Majumder和Malldl[9]计算的5.2 d基本一致。然而,157例确诊病例从发病到就诊的时间为0.5~11 d,M仅为0.5 d。此外,重点地区判定、封闭式管理有效控制了COVID-19的社区传播。有研究报道,根据COVID-19聚集性疫情特征分析结果显示,每控制一起家庭聚集疫情发生,可减少4名确诊病例;每减少一次聚餐,可避免5名病例发生,尤其是单位及商场等公共场所,做好防控可有效降低发病率[3]。宁波市开展了严格的医学观察措施,做到应收尽收,其中63.1%的确诊病例在发病前已经被隔离医学观察,使得病例在就医或其他日常生活接触过程中传播概率大幅度下降。本研究结果显示,自1月23日管控措施开始落实,模型拟合曲线中易感人群的接触概率明显下降。特别是2月4-5日开展的一系列防控措施,使疫情快速下降,防控成效明显。
SEIR-QAH传播动力学模型在SEIR模型的基础上,增加了隔离人群、无症状感染者、住院隔离治疗者等。该模型具有一定的普适性,可以为评价干预措施效果提供参考。在COVID-19疫情早期,一些采用SEIR模型进行流行趋势估计的研究结果显示,其R0为2.0~3.3之间[9-10]。疫情发生后,如果采取防控干预措施得当,疫情就会得到控制。此时动力学模型结果可作为参照,来评价防控措施的效果。同时,如何在疫情快速上升期、平台期和下降期等不同阶段使用该模型框架从而得到合理有效的预测结果成为目前研究的重点[11-12]。本研究通过收集宁波市新冠报告病例流行病学信息及人口学等数据,估算得出宁波市R0为4.8,高于已有研究得出的疫情初期R0[3]。随着防控措施的加强,Rt逐渐下降。到2月4日下降至1.0以下,之后持续下降到2月中旬的0.2。2月9日,企业陆续复工后,未出现明显的疫情波动。
本模型存在局限性。首先,建立SEIR模型的数据是动态数据,数据收集受时效性以及管控措施落实力度等因素影响,模型的参数是通过文献和数学模型拟合估计,预测与实际成效可能存在一定偏差;其次,随着确诊病例的及时发现与治疗,易感人群接触传染源的概率会有所降低,理想化的模型可能会高估Rt的下降趋势。
利益冲突 所有作者均声明不存在利益冲突
| [1] |
Zhu N, Zhang DY, Wang WL, et al. A novel coronavirus from patients with pneumonia in China, 2019[J]. N Engl J Med, 2020, 382(8): 727-733. DOI:10.1056/NEJMoa2001017 |
| [2] |
Li Q, Guan XH, Wu P, et al. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia[J/OL]. N Engl J Med, 2020. DOI: 10.1056/NEJMoa2001316.
|
| [3] |
中华预防医学会新型冠状病毒肺炎防控专家组. 新型冠状病毒肺炎流行病学特征的最新认识[J]. 中华流行病学杂志, 2020, 41(2): 139-144. Special Expert Group for Control of the Epidemic of Novel Coronavirus Pneumonia of the Chinese Preventive Medicine Association. An update on the epidemiological characteristics of novel coronavirus pneumonia (COVID-19)[J]. Chin J Epidemiol, 2020, 41(2): 139-144. DOI:10.3760/cma.j.issn.0254-6450.2020.02.002 |
| [4] |
World Health Organization. Novel Coronavirus (2019-nCoV) Situation Report-49[EB/OL].(2020-03-09)[2020-03-10].https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200309-sitrep-49-covid-19.pdf?sfvrsn=70dabe61_4.
|
| [5] |
中华人民共和国国家卫生健康委员会.截至3月9日24时新型冠状病毒肺炎疫情最新情况[EB/OL]. (2020-03-10)[2020-03-10]. http://www.nhc.gov.cn/xcs/yqtb/202003/948a03ad76f54d3583a018785efd7be9.shtml. National Health Commission of the People's Republic of China. An update of COVID-19 outbreak as of 24: 00 on 9 March[EB/OL].(2020-03-10)[2020-03-10]. http://www.nhc.gov.cn/xcs/yqtb/202003/948a03ad76f54d3583a018785efd7be9.shtml. |
| [6] |
中国疾病预防控制中心新型冠状病毒肺炎应急响应机制流行病学组. 新型冠状病毒肺炎流行病学特征分析[J]. 中华流行病学杂志, 2020, 41(2): 145-151. Special Expert Group for Control of the Epidemic of Novel Coronavirus Pneumonia of the Chinese Preventive Medicine Association. The epidemiological characteristics of an outbreak of 2019 novel coronavirus diseases (COVID-19) in China[J]. Chin J Epidemiol, 2020, 41(2): 145-151. DOI:10.3760/cma.j.issn.0254-6450.2020.02.003 |
| [7] |
Chen TM, Rui J, Wang QP, et al. A mathematical model for simulating the phase-based transmissibility of a novel coronavirus[J]. Infect Dis Poverty, 2020, 9(1): 24. DOI:10.1186/s40249-020-00640-3 |
| [8] |
杨海燕, 徐洁, 李岩, 等. 新型冠状病毒肺炎聚集性疫情特征初步分析[J]. 中华流行病学杂志, 2020, 41(5): 623-628. Yang HY, Xu J, Li Y, et al. The preliminary analysis on the characteristics of the cluster for the Corona Virus Disease[J]. Chin J Epidemiol, 2020, 41(5): 623-628. DOI:10.3760/cma.j.cn112338-20200223-00153 |
| [9] |
Majumder MS, Mandl KD. Early transmissibility assessment of a novel coronavirus in Wuhan, China[J/OL]. SSRN Electronic J, 2020. DOI: 10.2139/ssrn.3524675.
|
| [10] |
Riou J, Althaus CL. Pattern of early human-to-human transmission of Wuhan 2019 novel coronavirus (2019-nCoV), December 2019 to January 2020[J]. Euro Surveill, 2020, 25(4): 2000058. DOI:10.2807/1560-7917.ES.2020.25.4.2000058 |
| [11] |
魏永越, 卢珍珍, 杜志成, 等. 基于改进的SEIR+CAQ传染病动力学模型进行新型冠状病毒肺炎疫情趋势分析[J]. 中华流行病学杂志, 2020, 41(4): 470-475. Wei YY, Lu ZZ, Du ZC, et al. Fitting and forecasting the trend of COVID-19 by SEIR+CAQ dynamic model[J]. Chin J Epidemiol, 2020, 41(4): 470-475. DOI:10.3760/cma.j.cn112338-20200216-00106 |
| [12] |
唐三一, 肖燕妮, 彭志行, 等. 新型冠状病毒肺炎疫情预测建模、数据融合与防控策略分析[J]. 中华流行病学杂志, 2020, 41(4): 480-484. Tang SY, Xiao YN, Peng ZH, et al. Prediction modeling with data fusion and prevention strategy analysis for the COVID-19 outbreak[J]. Chin J Epidemiol, 2020, 41(4): 480-484. DOI:10.3760/cma.j.cn112338-20200216-00107 |
 2020, Vol. 41
2020, Vol. 41