中华流行病学杂志  2020, Vol. 41 Issue (9): 1460-1464   PDF    
http://dx.doi.org/10.3760/cma.j.cn112338-20191024-00761
中华医学会主办。
0

文章信息

汪业胜, 王胜难, 潘金花, 王伟炳.
Wang Yesheng, Wang Shengnan, Pan Jinhua, Wang Weibing
我国2009－2018年病毒性肝炎的发病趋势分析和预测研究
Trend analysis and prediction of viral hepatitis incidence in China, 2009-2018
中华流行病学杂志, 2020, 41(9): 1460-1464
Chinese Journal of Epidemiology, 2020, 41(9): 1460-1464
http://dx.doi.org/10.3760/cma.j.cn112338-20191024-00761

文章历史

收稿日期: 2019-10-24
引用本文
汪业胜, 王胜难, 潘金花, 王伟炳. 我国2009－2018年病毒性肝炎的发病趋势分析和预测研究[J]. 中华流行病学杂志, 2020, 41(9): 1460-1464
Wang Yesheng, Wang Shengnan, Pan Jinhua, Wang Weibing. Trend analysis and prediction of viral hepatitis incidence in China, 2009-2018[J]. Chinese Journal of Epidemiology, 2020, 41(9): 1460-1464.
我国2009－2018年病毒性肝炎的发病趋势分析和预测研究
汪业胜1 , 王胜难2 , 潘金花1 , 王伟炳1     
1. 复旦大学公共卫生学院流行病学教研室, 公共卫生安全教育部重点实验室, 上海 200032;
2. 上海市普陀区疾病预防控制中心 200333
收稿日期: 2019-10-24
基金项目: 国家科技重大专项（2017ZX10201302）；国家自然科学基金（81673233）
通信作者: 王伟炳, Email:wwb@fudan.edu.cn
汪业胜和王胜难对本文有同等贡献
摘要: 目的 探讨我国5种病毒性肝炎（肝炎）的时间序列特征，并通过有效的模型预测其发病率。方法 按照甲型肝炎、乙型肝炎、丙型肝炎、戊型肝炎和未分型肝炎5种不同类型肝炎分类方式收集2009－2018年的月度发病数据，进行描述性和时间序列研究，采用趋势分解法以季节指数形式表示时间序列中的季节性，以线性回归模型表示其长期趋势，为每种肝炎建立差分自回归移动平均（ARIMA）模型。结果 2009－2018年报告肝炎14 856 990例，5种肝炎季节指数的极差均 < 1，戊型肝炎的季节性特征较为显著，其发病呈单峰型，其余4种肝炎的季节性特征一般。甲型肝炎、戊型肝炎和未分型肝炎的发病基本趋于平稳，在一个较低的水平上呈缓慢下降趋势，乙型肝炎发病数在5种肝炎中占比最高（79.59%，11 824 262/14 856 990），但其下降趋势也为各型肝炎中最快（-0.01/10万）。丙型肝炎发病呈不断上升的趋势，上升速率一直保持稳定（0.005/10万）。ARIMA模型拟合的2009年1月至2018年12月的预测值与实际值较一致，平均绝对误差百分比范围为3.756 8~8.068 3。结论 对于法定报告传染病监测数据的时间序列分析有助于更好地了解我国肝炎的发病特征，ARIMA模型可用于我国肝炎的短期预测，具有较好的应用价值。
关键词: 病毒性肝炎    时间序列分解    季节性    长期趋势    预测    
Trend analysis and prediction of viral hepatitis incidence in China, 2009-2018
Wang Yesheng1 , Wang Shengnan2 , Pan Jinhua1 , Wang Weibing1     
1. Department of Epidemiology, School of Public Health, Key Laboratory of Public Health Safety of Ministry of Education, Fudan University, Shanghai 200032, China;
2. Shanghai Putuo District Center for Disease Control and Prevention, Shanghai 200333, China
Wang Yesheng and Wang Shengnan contributed equally to the article
Corresponding author: Wang Weibing, Email:wwb@fudan.edu.cn.
Fund program: National Science and Technology Major Project of China (2017ZX10201302); National Natural Science Foundation of China (81673233)
Abstract: Objective To explore the time series characteristics of 5 types of viral hepatitis in China and predict their incidence through effective models. Methods The monthly incidence data of 5 types of viral hepatitis (A, B, C, D and unspecified) in China from 2009 to 2018 were collected for descriptive and time series analyses, decomposition methods were used to explore the seasonality in the form of seasonal indices and the long-term trend in the form of a linear regression model. Autoregressive integrated moving average (ARIMA) models were established for each type of viral hepatitis. Results From 2009 to 2018, a total of 14 856 990 cases of viral hepatitis were reported, the seasonal index range of 5 types of viral hepatitis were all lower than 1, the seasonality of hepatitis E was significant, and its incidence was unimodal, but no obvious seasonality characteristics were observed for other four types of viral hepatitis. The incidences of hepatitis A, hepatitis E and unspecified hepatitis remained at lower levels, showing slow declines. Although the cases of hepatitis B accounted for the highest proportion (79.59%, 11 824 262/14 856 990) among 5 types of viral hepatitis, the decline was fastest (-0.01/100 000). The incidence of hepatitis C was on rise, and the rate of increase remained stable (0.005/100 000). The predicted incidences of 5 types of viral hepatitis in China from January 2009 to December 2018 fitted by ARIMA model were consistent with the actual incidences, and the mean absolute error percentage (MAPE) ranged from 3.756 8 to 8.068 3. Conclusions Time series analysis on surveillance data is useful for better understanding the incidence of the viral hepatitis. The ARIMA model has good application value in the short-term prediction of viral hepatitis incidence in China.
Key words: Viral hepatitis    Decomposition methods    Seasonality    Long-term trend    Prediction    

病毒性肝炎(肝炎)是由多种肝炎病毒引起的以肝脏病变为主的一种传染病, 肝炎大大加重了全球疾病负担, 甲型肝炎(甲肝)和戊型肝炎(戊肝)为全球广泛分布的肠道传染病, 通常为急性感染且可自愈.乙型肝炎(乙肝)和丙型肝炎(丙肝)为肠道外传染病, 全世界有2.48亿人感染乙肝, 7 100万人感染丙肝[1].如果不及时治疗, 慢性肝炎可能导致危及生命的并发症, 如肝硬化和肝细胞癌[2].我国是肝炎的高发区, 给社会和家庭带来沉重负担, 已成为我国严重的公共卫生问题之一.

时间序列分析以往多用于计量经济学的分析研究中, 近年来在传染病的预测分析中也广泛使用, 对于传染病的预测而言, 它可以很好地预测发病的长期趋势[3-4].本研究采用时间序列分解法, 分解出各型肝炎的发病季节性趋势和发病长期趋势, 根据两趋势相应的量化指标值大小探讨其发病趋势和季节性的显著程度以及发病高峰期、低谷期, 同时建立差分自回归移动平均(ARIMA)模型预测并评价其效果.

资料与方法

1.资料来源:国家卫生健康委员会疾病预防控制局网站公布的全国法定传染病月疫情统计数据.按照甲肝、乙肝、丙肝、戊肝和未分型肝炎的分类方式共收集了2009年1月至2018年12月公布的数据资料, 由于丁型肝炎(丁肝)疫情数据从2016年1月才开始作为单独分类, 因此在收集数据及后续分析时未纳入丁肝.

2研究方法:

(1) 趋势分解:时间序列一般包括长期趋势因素(T)、季节性因素(S)和随机性因素(R)3个部分, 趋势分解法常用于提取某种疾病发病时间序列中的不同成分[5-6], 该方法将疾病的时间序列分解成季节趋势和长期趋势, 传染病时间序列中的季节成分可以用季节指数来表示, 趋势分解法常用的模型有乘法模型和加法模型, 采用乘法模型进行时间序列的分解, 公式为: Xik=Tt×Sk, Xik表示第i年的第k个月的发病率, Tt表示无季节成分的时间序列, Sk表示第k个月的季节指数, Sk的计算方法分为三步[7]:

① 计算研究期间疾病在各个月份的平均发病率:

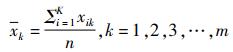
式中m表示第m个月, n表示总年数

② 计算研究期间疾病的平均发病率:

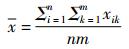
③ 计算各个月份的季节指数:

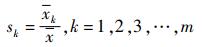
传染病时间序列中的季节成分通常是由于降雨、温度、以及节假日等因素引起的短期波动, 如果季节指数>1, 意味着该期间疾病的发病率高于平均水平, 相反, 如果季节指数 < 1, 则该期间疾病的发病率低于平均水平[5].得到疾病发病的季节指数之后, 采用乘法模型将疾病各个月份的发病率除以相应的季节指数, 即可得到其中的无季节效应部分.

其中的长期趋势可以通过构建无季节性序列(因变量)与时间(月份, 自变量)之间的线性回归模型来进行量化, 数学表达式为:

(2) ARIMA模型:由Box和Jenkins于20世纪70年代提出的一种时间序列的预测方法[8], 其基本思想是将预测对象随时间推移而形成的数据序列视为一组随机序列, 用一定的数学模型来近似描述这个序列, 从而根据已发生的既往序列值来预测未来值[9].它的一般形式为ARIMA(p, d, q), 因为传染病的发病大多具有季节周期性, 适合采用乘积季节模型ARIMA(p, d, q)(P, D, Q)s模型, 模型中p和q分别为非季节自回归阶数和非季节移动平均阶数, d为非季节差分阶数, P和Q分别是季节自回归阶数和季节移动平均阶数, D是季节差分的阶数, s是季节长度, ARIMA的乘积模型表达式为[9]:

其中:

ARIMA模型预测的基本步骤

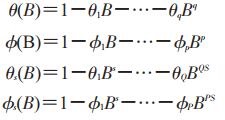
① 数据预处理: ARIMA模型要求待测的数据序列满足平稳性条件, 通过原始序列图、自相关和偏自相关图初步判断数据序列的平稳性, 采用ADF单位根检验来精确判断该序列的平稳性.对于非平稳的序列, 可以通过差分和季节差分处理, 直至其成为平稳的时间序列.

② 模型的识别:对于预处理后达到稳定性要求的序列, 绘制自相关图(autocorrelation function)和偏自相关图(partial autocorrelation function), 根据序列自相关图和偏自相关图建立相应的模型, 如果偏自相关函数p阶截尾, 选用AR(p)模型; 如果自相关函数q阶截尾, 选用MA(q)模型, 如果自相关函数和偏自相关函数都是拖尾的, 选用ARIMA(p, d, q)模型.参数P和Q的值较难判断, 一般采用从低阶到高阶逐步尝试的方法, 取值通常不超过2[10].

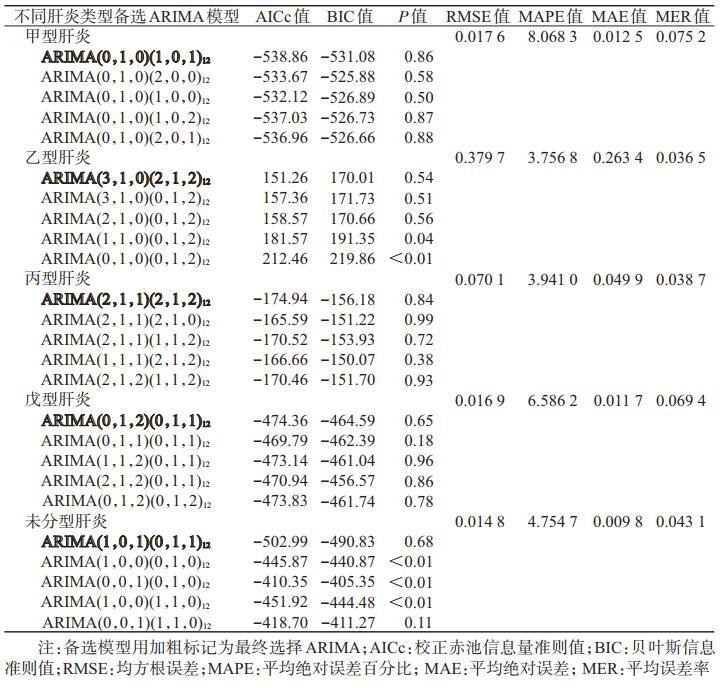
③ 参数估计和模型检验:在R软件中调用forecast包中的"fit()"函数运用最大似然估计法对模型参数进行估计, 再对备选模型的残差序列进行白噪声检验, 若统计量显示差异无统计学意义, 则表示残差为白噪声, 再通过对比备选模型的赤池信息量准则(AICc)和贝叶斯信息准则(BIC)值等系数, 选择AICc值和BIC值最小的模型为最佳ARIMA模型.

④ 预测:用5种肝炎2009年1月至2017年12月的发病数据作为训练集, 2018年1月至2018年12月的数据作为验证集, 计算各个最佳ARIMA模型的平均绝对误差百分比(MAPE)、均方根误差(RMSE)、平均绝对误差(MAE)和平均误差率(MER), 评价最佳模型的拟合和预测效果.

3.统计学分析:使用Excel 2019软件建立肝炎月发病数据库, 用SPSS 20.0软件对数据的季节性及长期趋势进行分析, 用R 3.6.1软件中的"forecast""ggplot2""tseries"包构建ARIMA模型.

结果

1. 5种肝炎的发病概况: 2009-2018年5种肝炎共报告病例数14 856 990例, 其中占比最高和最低的分别是乙肝11 824 262例(79.59%), 甲肝271 007例(1.82%).以血源和性传播为主的乙肝、丙肝占全部病例数的93.83%, 通过粪-口途径传播的甲肝、戊肝占全部病例数的3.69%.

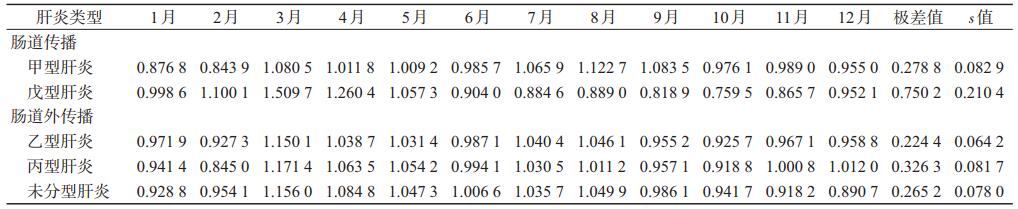
2. 5种肝炎发病的趋势分解:见表 1. 5种肝炎发病季节指数的极差均 < 1, 表明我国肝炎发病在2009-2018年期间基本趋于平稳, 个别虽有波动但幅度较小.通过肠道传播的甲肝和戊肝的季节特征较为明显, 尤其是戊肝的发病呈现出明显的单峰型, 每年的3月份为其发病高峰.相对而言, 肠道外传播的肝炎季节特征不明显或较为复杂, 往往一年内有多次发病高峰出现.

表 1 2009-2018年我国不同类型病毒性肝炎季节指数
表选项

表 2为疾病的长期趋势关于时间(月)的线性回归结果, 从中可以看出当去除季节性影响后, 发病率每月的平均变化趋势, 甲肝、戊肝和未分型肝炎发病的长期趋势与时间没有明显的关系, 其中甲肝和未分型肝炎从长远来看发病率呈下降的趋势(-0.001/10万), 但均较为缓慢.与之相比, 乙肝发病率下降的趋势则相对较快(-0.01/10万), 5种肝炎中, 只有丙肝表现出发病率上升的趋势(0.005/10万).

表 2 2009-2018年我国不同类型病毒性肝炎无季节效应发病率
表选项

3. ARIMA模型预测:用ARIMA模型预测5种肝炎的发病率, 根据统计学检验结果, 各自选择了5个备选模型, 其参数估计值和Ljung-Box残差检验结果, 见表 3.其中, P>0.05表示模型的残差为白噪声, 根据AICc值和BIC值最小原则确定最优模型, 以2009年1月至2017年12月的数据作为训练集, 2018年1月至2018年12月的数据作为验证集, 计算最优模型的RMSE、MAPE、MAE和MER.将模型拟合的2009年1月至2018年12月预测发病数与真实值比较发现(图 1), 模型预测的趋势与实际趋势一致.

表 3 2009——2018年我国不同类型病毒性肝炎的备选ARIMA模型及其参数值
表选项
图 1 2009-2018年我国不同类型病毒性肝炎月度发病率真实值及相应ARIMA模型拟合值
图选项
讨论

对肝炎时间序列中的季节性部分进行分析, 采用趋势分解方法将疾病的时间序列分解为季节趋势和长期趋势, 将季节趋势以季节指数的形式进行量化, 季节指数Sk>1, 说明季节性大于平均值, 出现流行高峰[11]. 5种肝炎中, 戊肝的季节性特征较为显著, 其发病呈单峰型, 在每年的3月份出现发病高峰, 由于戊肝属于肠道传播的传染病, 不卫生饮食习惯[12]、人与人之间的肢体接触[13]等都是戊肝发病的危险因素, 所以戊肝在3月份高发的原因可能是春节期间人们走亲访友, 接触被戊肝病毒污染食物的机会增加, 导致戊肝病毒在传染源与易感人群之间的传播.其余4种肝炎的季节性特征一般, 提示在一年四季均要做好相关的防控工作, 但是季节性不显著不代表其发病无高峰和低谷, 例如甲肝在1-3月份病例数相对最少, 6-9月份病例数相对多一些.

根据趋势分解假设, 提取季节指数后, 时间序列中仍存在长期趋势和随机因素, 对长期趋势建模有助于了解疾病的流行特征, 为公共卫生管理和疫苗制备提供参考.通过构建无季节性序列与时间之间的线性回归模型, 来量化肝炎发病的长期趋势.结果显示, 甲肝、戊肝的发病基本趋于平稳, 在一个较低的水平上呈缓慢的下降趋势, 说明随着政府加大对环境卫生和饮食卫生的改善力度、农村卫生条件的改善、人民群众卫生意识的提高、甲肝疫苗的大规模推广使用等[14-15], 对甲肝等肠道传播传染病的防控工作取得一定效果.乙肝和丙肝两种肠道外传播的肝炎, 其发病趋势却表现截然相反, 虽然乙肝发病数在5种肝炎中占比最高(79.59%), 但其长期发病趋势也为5种肝炎中下降最快, 在不断推广乙肝疫苗接种等防控措施作用下, 我国乙肝防控已取得明显效果.而丙肝发病则呈不断上升的趋势, 上升速率一直保持稳定, 这主要是由于慢性丙肝发病隐匿, 症状不明显, 丙肝很难被早期发现, 很多发病者实际上是数年前感染而最近才被检测, 此外, 丙肝病毒诊断率很低, 尤其是在欠发达地区, 很多丙肝病毒感染者未被确诊或被误诊, 这些因素共同导致丙肝的发病率呈上升趋势.未分型肝炎作为一种非独立的肝炎类别, 其作为单独分类是因为部分基层医疗机构不能区分开肝炎的具体类型, 随着肝炎临床诊断水平的逐年提高, 呈现出未分型肝炎逐渐减少的趋势.

利用2009-2018年的月发病率数据, 为每种肝炎都建立了ARIMA模型, 利用该模型拟合2009-2018年各型肝炎的发病趋势, 结果显示预测曲线与实际曲线较一致, RMSE范围0.014 8~0.379 7, MAPE范围3.756 8~8.068 3, MAE范围0.009 8~0.263 4, MER范围0.036 5~0.075 2, 一般认为MAPE低于10%~15%时预测精度较好[16], 提示不同类型肝炎各自的最优ARIMA模型对发病率的拟合效果较好, 可用于我国各型肝炎的短期预测和动态分析.

综上所述, 对于法定报告传染病监测数据的时间序列分析有助于更好地了解我国肝炎的发病特征, ARIMA模型可用于我国肝炎的短期预测, 具有较好的应用价值.但是, 时间序列分解法也具有其缺点, 在季节性的判断标准上, 无法获得统计指标证明显著性, 对于季节性特征显著与否、高峰期月份的判断带有主观因素.此外, 本研究数据来源于全国肝炎疫情报告资料, 影响报告发病率的因素有很多, 存在着重报、漏报、迟报、误报等, 在利用数学模型进行预测时, 应将这些因素考虑在内, 在以后的研究中应对模型进行优化, 以便更准确地分析和预测肝炎的发病情况.

利益冲突  所有作者均声明不存在利益冲突

参考文献
[1]
World Health Organization. Global hepatitis report 2017[R]. Geneva, Switzerland: World Health Organization, 2017.
[2]
Schweitzer A, Horn J, Mikolajczyk RT, et al. Estimations of worldwide prevalence of chronic hepatitis B virus infection:a systematic review of data published between 1965 and 2013[J]. Lancet, 2015, 386(10003): 1546-1555. DOI:10.1016/S0140-6736(15)61412-X
[3]
朱宗元, 于青. ARIMA模型在我国病毒性肝炎发病率预测中的应用[J]. 中国卫生统计, 2011, 28(1): 65-67.
Zhu ZY, Yu Q. Application of ARIMA model in predicting the incidence of viral hepatitis in China[J]. Chin J Health Statist, 2011, 28(1): 65-67. DOI:10.3969/j.issn.1002-3674.2011.01.022
[4]
蔡晓虹, 何明祯, 周洲, 等. 时间序列ARIMA模型在乙型肝炎疫情预测中的应用[J]. 世界感染杂志, 2010, 10(1/2): 25-28.
Cai XH, He MZ, Zhou Z, et al. Forecasting Hapetitis B epidemic situation by applying the ARIMA model[J]. World J Infect, 2010, 10(1/2): 25-28.
[5]
Zhang XY, Hou FS, Li XS, et al. Study of surveillance data for class B notifiable disease in China from 2005 to 2014[J]. Int J Infect Dis, 2016, 48: 7-13. DOI:10.1016/j.ijid.2016.04.010
[6]
Zhang XY, Zhang T, Young AA, et al. Applications and comparisons of four time series models in epidemiological surveillance data[J]. PLoS One, 2014, 9(2): e88075. DOI:10.1371/journal.pone.0088075
[7]
Zhang XY, Hou FS, Qiao ZJ, et al. Temporal and long-term trend analysis of class C notifiable diseases in China from 2009 to 2014[J]. BMJ Open, 2016, 6(10): e11038. DOI:10.1136/bmjopen-2016-011038
[8]
方积乾, 陆盈. 现代医学统计学[M]. 北京: 人民卫生出版社, 2002.
Fang JQ, Lu Y. Advanced medical statistics[M]. Beijing: People's Medical Publishing House, 2002.
[9]
王燕. 应用时间序列分析[M]. 北京: 中国人民大学出版社, 2005.
Wang Y. Application of time series analysis[M]. Beijing: China Renmin University Press, 2005.
[10]
言晨绮, 王瑞白, 刘海灿, 等. ARIMA模型预测2018-2019年我国肺结核发病趋势的应用[J]. 中华流行病学杂志, 2019, 40(6): 633-637.
Yan CQ, Wang RB, Liu HC, et al. Application of ARIMA model in predicting the incidence of tuberculosis in China from 2018 to 2019[J]. Chin J Epidemiol, 2019, 40(6): 633-637. DOI:10.3760/cma.j.issn.0254-6450.2019.06.006
[11]
Grassly NC, Fraser C. Seasonal infectious disease epidemiology[J]. Proc Roy Soc B:Biol Sci, 2006, 273(1600): 2541-2550. DOI:10.1098/rspb.2006.3604
[12]
姜梅, 崔伟红, 李波, 等. 烟台市戊型肝炎流行特征及危险因素分析[J]. 中华流行病学杂志, 2010, 31(12): 1417-1420.
Jiang M, Cui WH, Li B, et al. Epidemiological study on risk factors of hepatitis E in Yantai, Shandong province[J]. Chin J Epidemiol, 2010, 31(12): 1417-1420. DOI:10.3760/cma.j.issn.0254-6450.2010.12.022
[13]
Teshale EH, Grytdal SP, Howard C, et al. Evidence of person-to-person transmission of hepatitis E virus during a large outbreak in Northern Uganda[J]. Clin Infect Dis, 2010, 50(7): 1006-1010. DOI:10.1086/651077
[14]
张秀春, 韩莉莉, 邢玉兰, 等. 甲型肝炎灭活疫苗及减毒活疫苗对不同人群免疫效果的研究[J]. 中国计划免疫, 2002, 8(5): 254-257.
Zhang XC, Han LL, Xing YL, et al. A study on immune effects of hepatitis A vaccines to different persons with different schedules[J]. Chin J Vacc Immunizat, 2002, 8(5): 254-257.
[15]
Martin A, Lemon SM. Hepatitis A virus:from discovery to vaccines[J]. Hepatology, 2006, 43(Suppl1): S164-172. DOI:10.1002/hep.21052
[16]
Li Z, Wang Z, Song H, et al. Application of a hybrid model in predicting the incidence of tuberculosis in a Chinese population[J]. Infect Drug Resist, 2019, 12: 1011-1020. DOI:10.2147/IDR.S190418