文章信息
- 林静静, 张铁威, 李秀央.
- Lin Jingjing, Zhang Tiewei, Li Xiuyang
- 疾病时空聚集分析的研究与进展
- Research progress on spatiotemporal clustering of disease
- 中华流行病学杂志, 2020, 41(7): 1165-1170
- Chinese Journal of Epidemiology, 2020, 41(7): 1165-1170
- http://dx.doi.org/10.3760/cma.j.cn112338-20190806-00582
-
文章历史
收稿日期: 2019-08-06
疾病的时空聚集性是指疾病的发生在时间、空间或时空上的聚集倾向或趋势。现有研究发现时空聚集性普遍存在于传染病和慢性病发病的时空分布,这与地理环境因素、社会因素有关[1-4]。疾病的时空聚集性研究旨在了解疾病在时空上的分布特点和规律,帮助找出疾病高发时间段和高发区,从时间和空间探索人群的疾病与季节、地理环境等相关因素的关系,为疾病防治和医疗资源的合理配置提供理论依据。随着我国公共卫生信息系统的不断完善和地理信息系统的发展,具有空间属性的疾病和健康数据与日俱增。与此同时,各种时空统计学方法不断涌现,为探测疾病的时空聚集性提供了重要工具。本文旨在梳理近年来在疾病聚集性分析中常用的统计学方法及其应用进展,为今后相关研究提供参考依据。
一、时间聚集性1.圆形分布法:常用于分析具有周期性变化的资料,通过角度换算把每一个原始数据当做圆周上的一个位置的数据,并检验数据在一个周期内是否有集中分布的倾向。假设以1年为周期,1年若以365 d计算,1 d占360°圆周角的1/365,相当于0.986 3°。计算时先定下0角度对应的日期作为起始时点,将月、日记录化为距离0°日期的天数,再将天数乘上360°/365,转换为角度。再通过以下公式计算出平均角α:
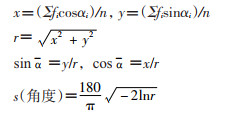
以平均角换算得到的日期为发病高峰日,以平均角±标准差算得到的日期范围为发病高峰期[5]。圆形分布法适用于单峰分布或略呈现双峰分布的疾病,常应用于发病呈季节性趋势的传染病研究。然而对于一个观察周期内出现多个高峰且高峰水平相当的疾病,圆形分布法并不能给出合理的结果[6],对于此种情况,有研究提出将多个高峰进行拆分,分别进行分析,可得到较为准确的结果[7]。理论上,以平均角±1.96标准差计算得到的95%参考值范围表示发病高峰日期更合适。
2.集中度法:集中度是发病时间季节性强弱的指标,表示疾病在一年内的聚集程度,由各月发病数与全年发病总数之比计算得出集中度m:
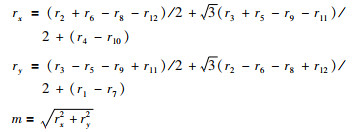
式中ri表示月发病数与全年发病数之比。m取值范围为0~1,m越大表明发病时间季节性越强,m越小表明发病时间分布越均匀。集中度法的不足在于仅说明疾病的发病时间呈现季节性的程度,但对于疾病发病具体的集聚时间无法估算,因此可将集中度法和圆形分布法联合使用探索疾病发病时间的聚集情况。
3.时间序列分析:是通过探索已知的时间序列规律构建模型来预测未来的一种方法。目前最常用的时间序列模型是自回归滑动平均模型(autoregressive integrated moving average,ARIMA)[8]。ARIMA模型的一般形式:
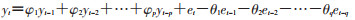
式中,yt是第t期的观测值,p是自回归的阶数,q是滑动平均的阶数,et是第t期的误差。当模型中不包含前几期的误差项时即为自回归模型,当模型中不包含前几期的观测值项时,即为滑动平均模型。如果时间序列不平稳,需要预先对序列进行差分处理直至平稳。因此可标记ARIMA为(p,d,q),d为差分阶数,p、q可以通过绘制序列的自相关函数图和偏自相关函数图并与标准图对比进行确定。当时间序列存在季节性的变化趋势时,采用ARIMA模型预测和拟合效果不太理想,应该考虑季节性回归差分移动平均模型(seasonal autoregressive integrated moving average,SARIMA),在ARIMA模型基础上引入季节性自回归的阶、季节性差分的阶和季节性移动平均的阶这3个参数。ARIMA法的主要局限是只能进行短期预测,以及线性模型和序列平稳假设。为了克服这些问题尤其是线性模型的局限,众多学者提出双线性模型[9]、门限自回归模型[10]等非线性模型。常用于时间序列分析的软件有SPSS、SAS、R软件等。
二、空间聚集性空间聚集性探测包括全局空间聚集性探测和局部空间聚集性探测,前者探索研究区域整体的聚集情况,后者可对局部区域进行聚集性分析,对聚集区进行定位。
一、全局空间聚集性1. Poisson分布和负二项分布法:Poisson分布法和负二项分布法是早期探测疾病聚集性的常用方法,前者描述的是罕见事件的概率分布,后者是一种非随机性的聚集性分布概率模型。Poisson分布法通过模型公式计算出事件的理论频数,再与实际频数进行拟合优度χ2检验确定分布状态是否符合Poisson分布,若符合,则不存在聚集性。负二项分布法的原理和Poisson分布法相似,拟合结果若满足负二项分布说明存在空间聚集性,还可以通过参数k衡量聚集程度,k值越小,聚集程度越大[11]。Poisson分布法和负二项分布法在使用前需要对疾病的空间分布模式进行合理假设,因此,当对某疾病的流行病学特征信息掌握较少难以建立空间分布模型时,使用该法存在一定的局限性[12]。
2. Ripley’s K函数法:K函数法由Ripley[13]提出,它将区域内的病例标识在地图上,按照一定半径d的搜索圆范围来统计点数量,对所有样本点对之间的距离计算其平均值,最后用该平均值除以研究区域内的样本点密度,得到函数值k(d):
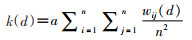
a为研究区域面积,n为研究区域内样本点数量,wij(d)为在半径d的搜索圆内的样本点i和样本点j之间的距离。为保持方差稳定,Besag[14]后来又提出用l(d)替代k(d),其转换公式为: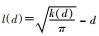
在完全随机分布假设下,l(d)=0;l(d)<0,则认为病例呈均匀分布;l(d)>0,则认为病例呈聚集分布。空间聚集性的假设检验采用蒙特卡罗法,获得不同距离尺度的l(d)的置信区间,并绘制包络线。当实际算得的l(d)位于包络线上,则认为存在空间聚集性,偏离其随机置信区间最大的l(d)值作为最大聚集强度指标,而以该最大聚集强度为半径的圆表示最大聚集规模[15]。Rispley’s K函数法能以一系列连续尺度确定点要素在给定范围内随距离变化的聚集性变化情况,该法发展至今扩展出许多新的方法,如网络K函数[16]、单变量与双变量K函数等[17],对分布模式可提供更多信息。常用来分析Rispley’s K函数的统计软件有Crimestat、Matlab、R软件等。
3.最邻近指数(nearest neighbor indicator,NNI):最邻近距离统计是通过比较计算最邻近的点对的平均距离与随机分布模式中最邻近的点对的平均距离,用NNI判断其与随机分布的偏离[18]。计算公式:
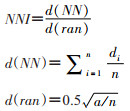
d(NN)为每个点要素与其最近邻点之间的平均距离;n为样本点数目;di为i点到最邻近点的距离;d(ran)为随机分布下的理论平均距离;a为研究区域面积。
当样本点随机分布时,NNI=1;样本点聚集时,NNI<1;样本点较随机分布更加发散时,NNI>1。基于NNI原理,可以进一步对样本进行聚类,即最邻近层次空间聚类分析[19],当观察点间距离小于理论距离,则将该点计入聚集单元,如此将点数据聚类为若干区域,称为一阶聚类,通过类似原理,可以再得到更高阶的聚类,直到再也找不到任何集群。Crimestat软件是运行NNI法的常用软件。
4. Cuzick-Edward法[20]:基于病例的空间位置和在研究区域内随机选择对照点,并计算每个病例的k个最邻近点中的病例数目的和tk:
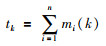
式中,k为最邻近数目,由用户指定;n表示病例数;mi(k)表示病例i的k个最邻近点中的病例数目。当疾病存在空间聚集时,每个病例最邻近往往是其他病例,因此tk较大;如果疾病病例离散分布,病例最邻近是对照点,tk为0。tk的假设检验可以与蒙特卡罗模拟的完全随机分布模式下的数进行比较。Cuzick-Edward法可通过ClusterSeer、R软件实现。
5.全局空间自相关法:指空间位置上距离越近的事物或现象就越相似,即事物或现象具有对空间位置的依赖关系,由空间自相关系数度量。全局空间自相关法常用的有Moran’s I、Geary’s C和Getis’s G 3种系数法(表 1)[21]。3种方法都假设研究区域不存在空间聚集分布,Moran’s I自相关系数通过比较目标要素的属性值和全部要素属性均值的差异度量空间自相关,Moran’s I统计量的取值为[-1, 1],I>0表示研究对象之间存在空间正相关,I<0则表示存在空间负相关,I=0表示空间随机分布;Geary’s C比较的是相邻要素属性的差异,取值范围是0~2,越接近0,空间正相关性越强;越接近2,负相关性越强;越接近1,数据越可能随机分布。Getis’s G测量在位置i上的数值与距离为d的范围内每个位置j上数值的相关程度,它不仅可以分析是否存在空间聚集区,还可以确定是高聚类还是低聚类。3种方法都可以通过蒙特卡罗模拟法进行假设检验。
1.局部空间自相关:全局自相关假定空间是同质的,即研究区域内的空间对象的某一属性值只存在一种整体趋势。当研究区域存在空间异质性时,全局自相关分析有时会掩盖局域存在的聚集性,此时采用局部自相关分析。局部空间自相关主要用局部自相关系数(local indicators of spatial autocorrelation,LISA)Moran’s I系数[22]和局部Getis系数[23]来反映探测变量在局部区域范围内的空间聚集性[20-21]。
Moran’s I的LISA定义如下:
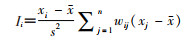
其中,x表示所研究区域的属性值的平均值,s2为方差,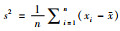
局部Getis系数又称“热点分析”,计算公式:
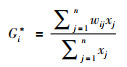
其假设检验方法与全局自相关假设检验方法一样。Gi*为正值,表明为空间正相关;Gi*为负值,表明为空间负相关。
在实际研究中,全局空间自相关常常用作疾病空间聚集性的探索性研究方法,局部空间自相关分析则对聚集区域进一步定位。如马永成等[24]对青海省结核病时空分布进行分析,先采用全局Moran’s I法分析发现青海省结核病存在空间正相关性,之后再采用Getis系数法找出了发病特征呈现高-高聚集和低-低聚集的区县。常用的空间自相关分析的统计软件是Geoda、ArcGIS和R软件。
2.核密度估计[25]:核密度估计法本身并不是一种检测聚类的技术,它只能生成连续密度分布图以便进一步直观上识别事件高发区域。该方法首先计算每个样本点其周围领域的概率密度,在一定距离h内距离该样本点越远,密度越小,到极限距离处密度为0。然后将相同位置处的密度进行叠加,从而得到整个研究区域的分布密度。假设x1,x2…xn为单变量x的n个样本点,则其概率密度函数fh(x)的核密度估计为:
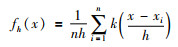
式中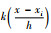
核函数和带宽的选择对核密度估计十分重要。常用的核函数有高斯核函数、Epanechnikov核函数等,选择不同的核函数对核密度估计结果影响不会很大,而带宽h对结果有较大影响[26]。h取值越小,核密度估计函数的曲线突兀不平,产生一定的噪声误差;h取值越大,会掩盖密度的细节部分,函数的曲线越光滑且概化程度越高。因此应根据实际情况选择合适的带宽,研究区域尺度、研究要素的特征等都会影响带宽的选择[27-28],除了固定带宽,有研究还提出自适应的带宽选择方法[29],可更好地识别空间密度差异,生成稳定的结果。核密度估计可通过ArcGIS、CrimeStat软件实现。
三、时空聚集性1. Knox时空交互模型:Knox法是一种全局时空聚集探测方法[30]。它首先人为设定空间阈值s和时间阈值t,将所有事件点两两配对,并计算空间距离sij和时间距离tij。当sij≤s时,认为事件点空间邻近;当tij≤t时,认为事件点时间邻近。根据事件是否时空邻近,对不同类别的事件对数进行计数,其中时空邻近事件对数即为Knox指数,假设检验采用χ2检验。
时空阈值的设定对于Knox检验结果具有关键作用,它决定了在哪一时空尺度下零假设将会被拒绝或接受。空间阈值通常由经验确定或借鉴其他领域研究结果,例如传染病的潜伏期和传播特点[31]。此外,一些学者提出了相关阈值确定方法,例如平均最邻近距离法、平均Rispley’s K函数临界值法[32]。Knox存在的最大不足是其结果受暴露人口变动的影响[33],对于潜伏期较长,发病率很高的传染病该方法效率不高。
2.时空扫描统计:时空扫描统计[34]既能单纯研究时间、空间的聚集规律,也能够同时考虑时间和空间两个因素。其原理是创建一个以研究的地理区域定义底面、时间间隔定义高度、风险人口定义半径的圆柱体扫描窗口,扫描窗口的大小和位置在研究区域内不断变化。然后对每一个扫描窗口,计算理论事件数,利用扫描窗口内外的实际值和理论值构造对数似然比(log-likelihood ratio,LLR)检验统计量,差异有统计学意义说明该动态窗口下的区域为聚集区,最终选取LLR值最大的窗口为高聚集窗口。LLR计算公式:
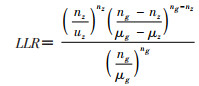
其中,nz表示时空窗口z中的事件数,ng是研究区域总事件数,uz是时空窗口z中的理论事件数,μg是研究区域总的理论事件数。
时空扫描统计不仅能揭示疾病聚集的具体时间并对聚集区域进行定位,还能得出聚集区域的相对危险度。该法存在的不足之处是圆形或椭圆形窗口不适用于不规则形状簇的检测,很多学者针对该问题提出解决方案。Iyengar[35]扩展了该方法,以检测具有方形金字塔形状的时空簇;Neill等[36]提出了检测矩形时空集群的算法;Takahashi等[37]开发了灵活形状的时空扫描统计,通过结合相邻区域信息,在子区域生成不规则形状的窗口。时空扫描统计法主要在SatScan软件上运行。
3.基于时空密度的聚类方法:时空扫描统计需要预先假定数据的概率分布模型,且结果受扫描窗口的影响较大,不能详细描述时空簇的位置和形状信息[38]。为了克服这些问题,近年来,越来越多基于时空密度的聚类方法被提出。时空密度聚类是空间密度聚类在时空域上的扩展,采用密度作为实体间相似性的度量标准,将时空簇看作一系列被低密度区域(噪声)分割的高密度连通区域[39],其中最常用的方法是ST-DBSCAN。
ST-DBSCAN法由DBSCAN增加时间维度扩展而来,其假设i和j为直接密度可达的两个核心点,如果两个核心点的邻域的非空间属性平均距离小于阈值,则对这两个邻域进行聚类[40]。ST-DBSCAN不需要预先假设数据的分布模型,且可以检测任意形状的聚集簇。目前该法多应用于道路交通领域,在疾病聚集方面的应用尚处于起步阶段。Guo等[41]采用ST-DBSCAN对2005-2011年中国狂犬病病例进行分析,共检测到480个聚类。该法存在的不足是需要设定空间、时间、非空间距离阈值和密度阈值,DBSCAN对用户定义的参数很敏感,因此如何选取合适的参数十分关键。很多研究对此提出解决对策,如基于窗口最近邻法[42]、自适应法[43]等确定阈值。基于时空密度的聚类方法是目前研究的热点,新方法不断提出,如时空不规则聚类法[44]、时空有序点识别聚类结构[45]、Bregman Block共聚类算法[46]等。
四、讨论疾病的时空聚集性分析是近年来研究十分热门的一个领域,相应的统计学方法也在不断完善。本文介绍的大部分统计学方法已广泛地应用于传染病与慢性非传染性疾病的时空分布模式探索,其中时空扫描统计量可同时分析疾病在时间和空间上的聚集且操作简单易行,受到众多学者青睐,近年来相关研究越来越多[47-49]。然而,新兴的方法如探测不规则形状时空簇的时空扫描统计法和基于时空密度的聚类方法在疾病领域的应用不是很多。这些方法解决了传统的时空扫描统计对于不规则聚集簇识别力弱的问题,提供了聚集簇形状和位置信息,在疾病聚集性研究方面显现出广阔的应用前景。
在选择和应用时空或空间统计学方法时应注意几个问题。一是本文所介绍的方法均适用于点数据的分析,即具体的病例地址数据,然而实际工作中容易获得的往往是区域病例汇总后的面数据。Cuzick-Edwards法、空间自相关法、时空扫描统计法也适用于面数据聚类分析[50],前提是需要对面数据作点处理,可以采用区域面的质心进行计算,面数据的空间分辨率较点数据低,时空聚集探测的能力会有所减弱[48]。二是本文讨论的统计学方法仍在不断发展中,在对疾病聚集性进行探索性分析时,建议采用多种方法联合分析,以尽可能提高识别的准确度,避免聚集区漏报、误报。三是地理信息系统在疾病时空聚集性分析中有着重要的作用,自相关分析、核密度估计、时空扫描统计量等方法基于GIS进行分析,通过地图进行可视化呈现,有助于结果的表达和传播。
总之,随着疾病时空数据的不断累积,时空统计方法的完善以及统计分析软件的升级,时空聚集性分析在疾病中的应用也不断发展。未来应继续加强获取疾病时空维度的数据,不断提高数据收集的精细化,深入开展疾病时空聚集性研究,使其在公共卫生监测和决策中发挥更大的作用。
利益冲突 所有作者均声明不存在利益冲突
| [1] |
王忠东, 孙海燕, 薛白, 等. 青岛市肺结核空间聚集性分析[J]. 预防医学论坛, 2015, 21(12): 959-960. Wang ZD, Sun HY, Xue B, et al. Analysis of spatial aggregation of pulmonary tuberculosis in Qingdao[J]. Prev Med Tribune, 2015, 21(12): 959-960. DOI:10.16406/j.pmt.issn.1672-9153.2015.12.031 |
| [2] |
刘东立, 邱琳, 石一, 等. 陕西省2004-2017年细菌性痢疾时空分布流行病学分析[J]. 中国卫生统计, 2019, 36(2): 176-180. Liu DL, Qiu L, Shi Y, et al. Epidemiological analysis of spatio-temporal distribution of bacterial dysentery in Shaanxi province, 2004-2017[J]. Chin J Health Statist, 2019, 36(2): 176-180. |
| [3] |
Kuo TM, Meyer AM, Baggett CD, et al. Examining determinants of geographic variation in colorectal cancer mortality in North Carolina:A spatial analysis approach[J]. Cancer Epidemiol, 2019, 59: 8-14. DOI:10.1016/j.canep.2019.01.002 |
| [4] |
Caswell JM. Prevalence of reported high blood pressure in Canada:investigation of demographic and spatial trends[J]. J Public Health, 2017, 25(1): 49-59. DOI:10.1007/s10389-016-0761-4 |
| [5] |
金丕焕. 医用统计学方法[M]. 上海: 复旦大学出版社, 2009. Jin PH. Medical statistical methods[M]. Shanghai: Fudan University Press, 2009. |
| [6] |
戴启刚. 圆分布的平均角及其区间估计方法在传染病发病高峰评估中的应用探讨[J]. 中国卫生统计, 2015, 32(1): 77-78, 81. Dai QG. Application of the mean angle of circular distribution and its interval estimation method in the assessment of the peak of infectious disease[J]. Chin J Health Statist, 2015, 32(1): 77-78, 81. |
| [7] |
李涛, 魏雄杰, 张华林, 等. 应用圆形分布探讨肾综合征出血热的季节性[J]. 中国卫生统计, 2015, 32(6): 1029-1030. Li T, Wei XJ, Zhang HL, et al. Study on the seasonality of hemorrhagic fever with renal syndrome by circular distribution[J]. Chin J Health Statist, 2015, 32(6): 1029-1030. |
| [8] |
Makridakis SG, Wheelwright SC, Hyndman RJ. Forecasting:methods and applications[M]. London: John Wiley & Sons, 1998.
|
| [9] |
Bollerslev T. Generalised autoregressive conditional heterosce-dasticity[J]. J Econometr, 1986, 31(3): 307-327. DOI:10.1016/0304-4076(86)90063-1 |
| [10] |
Casdagli M. Nonlinear prediction of chaotic time series[J]. Phys D:Nonlinear Phenom, 1989, 35(3): 335-356. DOI:10.1016/0167-2789(89)90074-2 |
| [11] |
郭祖超. 医用数理统计方法[M]. 3版. 北京: 人民卫生出版社, 1988. Guo ZC. Medical mathematical statistics[M]. 3rd ed. Beijing: People Hygiene Press, 1988. |
| [12] |
薛付忠, 王洁贞, 马希兰. 疾病空间分布状态的负二项分布概率生成模型的讨论[J]. 中国卫生统计, 2000, 17(6): 366-368. Xue FZ, Wang JZ, Ma XL. Discussion on the probability generation model of negative binomial distribution of disease spatial distribution[J]. Chin J Health Statist, 2000, 17(6): 366-368. DOI:10.3969/j.issn.1002-3674.2000.06.019 |
| [13] |
Ripley BD. Modelling spatial patterns[J]. J Roy Statist Soc Series B Methodol, 1977, 39(2): 172-212. DOI:10.1111/j.2517-6161 |
| [14] |
Besag JE. Comment on "Modelling spatial patterns" by B.D. Ripley[J]. J Roy Statist Soc Ser B Statist Methodol, 1977, 39: 73-78. |
| [15] |
高杰, 王志强, 邵琦, 等. Ripley's L指数与最近邻空间热点分析在流行病学标点地图分析中的应用[J]. 山东大学学报:医学版, 2009, 47(3): 89-93, 97. Gao J, Wang ZQ, Shao Q, et al. Ripley's L index and the Nearest Neighbor 'hot spots' analysis in epidemiological spots map analysis[J]. J Shandong Univ:Health Sci, 2009, 47(3): 89-93, 97. |
| [16] |
Spooner PG, Lunt ID, Okabe A, et al. Spatial analysis of roadside Acacia populations on a road network using the network K-function[J]. Landscape Ecol, 2004, 19(5): 491-499. DOI:10.1023/b:land.0000036114.32418.d4 |
| [17] |
Li L, Huang ZL, Ye WH, et al. Spatial distributions of tree species in a subtropical forest of China[J]. Oikos, 2009, 118(4): 495-502. DOI:10.1111/j.1600-0706.2009.16753.x |
| [18] |
Clark PJ, Evans FC. Distance to nearest neighbor as a measure of spatial relationships in populations[J]. Ecology, 1954, 35(4): 445-453. DOI:10.2307/1931034 |
| [19] |
Everett B. Cluster analysis[M]. London: Heinemann Educational Books Ltd., 1974.
|
| [20] |
Cuzick J, Edwards R. Spatial clustering for inhomogeneous populations[J]. J Roy Statist Soc Methodol, 1990, 52(1): 73-104. |
| [21] |
Getis A, Cliff AD, Ord JK. 1973:Spatial autocorrelation. London:Pion[J]. Progress in Human Geography, 1973, 19(2): 245-249. DOI:10.1177/030913259501900205 |
| [22] |
Anselin L. Local indicators of spatial association-LISA[J]. Geogr Anal, 1995, 27(2): 93-115. DOI:10.1111/j.1538-4632.1995.tb00338.x |
| [23] |
Ord JK, Getis A. Local spatial autocorrelation statistics:distributional issues and an application[J]. Geogr Anal, 1995, 27(4): 286-306. DOI:10.1111/j.1538-4632.1995.tb00912.x |
| [24] |
马永成, 王兆芬, 李斌, 等. 基于GIS的青海省结核病时空分布特征研究[J]. 中华疾病控制杂志, 2018, 22(4): 340-344, 353. Ma YC, Wang ZF, Li B, et al. Temporal and spatial distribution of tuberculosis in Qinghai Province based on GIS[J]. Chin J Dis Control Prev, 2018, 22(4): 340-344, 353. DOI:10.16462/j.cnki.zhjbkz.2018.04.005 |
| [25] |
Gatrell AC, Bailey TC, Diggle PJ, et al. Spatial point pattern analysis and its application in geographical epidemiology[J]. Trans Instit British Geogr, 1996, 21(1): 256-274. DOI:10.2307/622936 |
| [26] |
Pfeiffer D, Robinson T, Stevenson M, et al. Spatial analysis in epidemiology[M]. New York: Oxford University Press, 2008.
|
| [27] |
Scott DW. Multivariate density estimation:theory, practice, and visualization[M]. New York: John Wiley & Sons, 1992.
|
| [28] |
Haining R. Spatial data analysis-theory and practice[M]. Cambridge: Cambridge University Press, 2003.
|
| [29] |
Shi X. Selection of bandwidth type and adjustment side in kernel density estimation over inhomogeneous backgrounds[J]. Int J Geogr Inf Sci, 2010, 24(5): 643-660. DOI:10.1080/13658810902950625 |
| [30] |
Knox EG, Bartlett MS. The detection of space-time interactions[J]. Appl Stats, 1964, 13(1): 25-29. DOI:10.2307/2985220 |
| [31] |
刘巧兰, 李晓松, 冯子健, 等. Knox方法在传染病时空聚集性探测中的应用[J]. 中华流行病学杂志, 2007, 28(8): 802-805. Liu QL, Li XS, Feng ZJ, et al. Study on the application of Knox method to temporal-spatial cluster for infectious diseases[J]. Chin J Epidemiol, 2007, 28(8): 802-805. DOI:10.3760/j.issn:0254-6450.2007.08.019 |
| [32] |
岳瀚, 朱欣焰, 呙维, 等. Knox时空交互检验空间阈值确定方法[J]. 武汉大学学报:信息科学版, 2018, 43(11): 1719-1724. Yue H, Zhu XY, Guo W, et al. A method for determining the critical spatial threshold of spatio-temporal interaction for the Knox test[J]. Geomat Inf Sci Wuhan Univ, 2018, 43(11): 1719-1724. DOI:10.13203/j.whugis20170017 |
| [33] |
Kulldorff M, Hialmarsu. The Knox method and other tests for space-time interaction[J]. Biometrics, 1999, 55(2): 544-552. DOI:10.1111/j.0006-341x.1999.00544.x |
| [34] |
Tango T. Statistical methods for disease clustering[M]. Takayasu: Springer Science+Business Media, 2010.
|
| [35] |
Iyengar VS. On detecting space-time clusters[C]//Proceedings of the Tenth 2004 ACM SIGKDD International Conference on Knowledge Discovery and Data Mining[M]. Washington, USA: 2004, 1: 587-592. DOI: 10.1145/1014052.1014124.
|
| [36] |
Neill DB, Moore AW, Sabhnani M, et al. Detection of emerging space-time clusters[C]//Proceedings of the Eleventh ACM SIGKDD International Conference on Knowledge Discovery in Data Mining[M].USA: Illinois, 2005: 218-227.
|
| [37] |
Takahashi K, Kulldorff M, Tango T, et al. A flexibly shaped space-time scan statistic for disease outbreak detection and monitoring[J]. Int J Health Geogr, 2008, 7: 14. DOI:10.1186/1476-072X-7-14 |
| [38] |
Pei T, Zhou CH, Zhu AX, et al. Windowed nearest neighbour method for mining spatio-temporal clusters in the presence of noise[J]. Int J Geogr Inf Sci, 2010, 24(6): 925-948. DOI:10.1080/13658810903246155 |
| [39] |
唐建波, 邓敏, 刘启亮. 时空事件聚类分析方法研究[J]. 地理信息世界, 2013, 20(1): 38-45. Tang JB, Deng M, Liu QL. On spatio-temporal events clustering methods[J]. Geomat World, 2013, 20(1): 38-45. DOI:10.3969/j.issn.1672-1586.2013.01.012 |
| [40] |
Birant D, Kut A. ST-DBSCAN:An algorithm for clustering spatial-temporal data[J]. Data Knowledge Eng, 2007, 60(1): 208-221. DOI:10.1016/j.datak.2006.01.013 |
| [41] |
Guo DH, Zhou H, Zou Y, et al. Geographical analysis of the distribution and spread of human rabies in China from 2005 to 2011[J]. PLoS One, 2013, 8(8): e72352. DOI:10.1371/journal.pone.0072352 |
| [42] |
Liu QL, Deng M, Bi JT, et al. A novel method for discovering spatio-temporal clusters of different sizes, shapes and densities in the presence of noise[J]. Int Jo Digit Earth, 2014, 7(2): 138-157. DOI:10.1080/17538947.2012.655256 |
| [43] |
Li ZL, Liu QL, Tang JB, et al. An adaptive method for clustering spatio-temporal events[J]. Trans GIS, 2018, 22(1): 323-347. DOI:10.1111/tgis.12312 |
| [44] |
Joshi D, Samal A, Soh LK. Spatio-temporal polygonal clustering with space and time as first-class citizens[J]. Geo Informatica, 2012, 17(2): 387-412. DOI:10.1007/s10707-012-0157-8 |
| [45] |
Agrawal KP, Garg S, Sharma S, et al. Development and validation of OPTICS based spatio-temporal clustering technique[J]. Inf Sci, 2016, 369: 388-401. DOI:10.1016/j.ins.2016.06.048 |
| [46] |
Ullah S, Daud H, Dass SC, et al. Detecting space-time disease clusters with arbitrary shapes and sizes using a co-clustering approach[J]. Geospat Health, 2017, 12(2): 567. DOI:10.4081/gh.2017.567 |
| [47] |
Fritz CE, Schuurman N, Robertson C, et al. A scoping review of spatial cluster analysis techniques for point-event data[J]. Geospat Health, 2013, 7(2): 183-198. DOI:10.4081/gh.2013.79 |
| [48] |
李秀央, 陈坤. 扫描统计量的理论及其在空间流行病学中的应用[J]. 中华流行病学杂志, 2008, 29(8): 828-831. Li XY, Chen K. Scan statistic theory and its application in spatial epidemiology[J]. Chin J Epidemiol, 2008, 29(8): 828-831. |
| [49] |
樊文洁, 王山, 曹红艳, 等. 时空统计方法[J]. 中华流行病学杂志, 2015, 36(1): 83-86. Fan WJ, Wang S, Cao HY, et al. Spatio-temporal statistical method[J]. Chin J Epidemiol, 2015, 36(1): 83-86. DOI:10.3760/cma.j.issn.0254-6450.2015.01.019 |
| [50] |
Ozonoff A, Jeffery C, Manjourides J, et al. Effect of spatial resolution on cluster detection:a simulation study[J]. Int J Health Geograph, 2007, 6(1): 52. DOI:10.1186/1476-072X-6-52 |
 2020, Vol. 41
2020, Vol. 41



