文章信息
- 唐林, 孙坤, 凌倩, 李东民.
- Tang Lin, Sun Kun, Ling Qian, Li Dongmin
- 贝叶斯统计在艾滋病疫情估计中的应用
- Application of Bayesian statistics in AIDS epidemic estimation
- 中华流行病学杂志, 2020, 41(3): 436-441
- Chinese Journal of Epidemiology, 2020, 41(3): 436-441
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2020.03.029
-
文章历史
收稿日期: 2019-06-04
随着艾滋病在世界各国的流行,波及的地域越来越广、人群更多,流行模式更为复杂,对艾滋病疫情估计和预测的方法也需要不断改进与完善。艾滋病疫情估计是基于历年病例报告数据、专题调查数据以及实验室标志物检测等监测数据,并通过一定的模型或方法对艾滋病流行地区的新发感染者数、患病数以及流行趋势等进行估计和预测,为当地艾滋病防治效果的评估以及卫生资源的分配提供依据[1-2];目前用于艾滋病疫情估计的方法主要有数理统计模型或方法,包括传染病动力学模型(Dynamic model)、自回归移动平均模型(ARIMA model)、灰色预测模型(Grey model)、马尔科夫模型(Markov model)、贝叶斯模型(Bayesian model)、改良反向计算法(Modified back-calculation method)等以及计算机软件预测方法,包括工作簿法(Workbook approach)、亚洲流行模型(AEM)、估计与预测软件包(EPP)和Spectrum软件,这些数理统计模型/方法和计算机软件预测方法各有其优缺点[3-4]。同时,由于艾滋病监测资料来源的多样性、HIV在不同地区、不同人群中流行的差异性及不同疫情估计方法各有其局限性,结合不同的疫情估计方法综合评估艾滋病疫情已成为一种趋势[3-4]。本文对既往贝叶斯统计应用于艾滋病疫情估计的研究进行综述,为贝叶斯统计在疫情估计中的进一步应用提供参考。
1.贝叶斯统计思想:
贝叶斯统计主要涉及总体信息、样本信息以及先验信息3种信息,其中先验信息是在抽样前对样本的认知,一般来源于经验或历史资料;对未知参数θ的认知是将其看成一个随机变量,并采用一个概率分布去描述,称之为先验分布;贝叶斯统计思想就是结合先验分布、样本信息以及总体信息对θ进行统计推断,得到一个关于θ的新分布,称之为后验分布,并通过高微积分求解得到相关统计量,如后验均值、中位数等;其中后验分布是利用抽样信息(总体信息和样本信息)对先验分布进行调整的结果,而先验分布的确定又依赖于先验信息的选取[5]。
贝叶斯公式(定理)是贝叶斯统计推断的核心,随机变量的贝叶斯公式为:
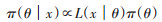
其中π=(θ)由参数θ的先验信息确定,称之为θ的先验密度函数(即先验分布),表示的是抽样前对θ的主观认知,即根据先验信息确定θ服从先验分布时的概率大小;L(x|θ)为似然函数,表示的是在给定参数θ下,样本X1,X2,…,Xn的条件密度函数;π=(θ|x)为后验密度函数,反映了抽样后对θ的认知,其综合了参数θ的先验信息与抽样信息,共同对θ进行统计推断[6]。
目前常用的马尔科夫链蒙特卡罗算法(Markov Chain Monte Carlo,MCMC)及R软件包,WinBUGS及相关统计软件等解决了贝叶斯统计高微积分等复杂的计算问题,尤其是Gibbs抽样作为MCMC中常用的抽样方式,促进了贝叶斯统计在各领域的发展[7-8]。
2.贝叶斯统计在艾滋病疫情估计中的发展:
(1)国外研究现状:贝叶斯统计思想于1982年逐渐地被医学领域所接受[9],但在艾滋病疫情估计中的应用最早始于1989年Taylor[10]和Zeger等[11]利用贝叶斯方法对美国HIV感染及艾滋病流行趋势进行预测,不过其应用仅限于利用贝叶斯统计对模型参数进行不确定性选择,并不涉及复杂的计算;随着艾滋病监测数据的丰富以及贝叶斯统计后验分布高微积分的计算得以解决,贝叶斯统计在艾滋病疫情估计中的应用大致可以分为3个阶段:第一阶段(1989-1996年),这一阶段贝叶斯统计在艾滋病疫情估计中的应用主要包括艾滋病流行平滑曲线的绘制[12]、CD4+T淋巴细胞(CD4)纵向数据分布规律的描述[13]、反向预测HIV新发感染数[14-15]等,其主要特征是根据不同的艾滋病监测资料选择合适的贝叶斯方法进行参数估计,对未知疫情进行预测;第二阶段(1997-2006年),这一阶段由于艾滋病抗病毒治疗的影响以及MCMC算法的优化,艾滋病疫情估计多倾向于联合其他艾滋病疫情估计方法如动力学模型[15-16]、改良反向计算法[17-18]、马尔科夫模型[19]等方法估计疫情,主要特征是结合多种估计方法分析疫情结果,并探讨贝叶斯统计在参数估计中先验分布的选取;第三阶段(2007年-至今),贝叶斯统计在艾滋病疫情估计中的应用自2006年后显著增加,应用范围越来越广,模型的选择也从早期的参数模型到半参数模型[20],从传统的线性模型到非线性模型[21-22],从固定效用模型到混合效应模型等扩展[23-25];此外,艾滋病疫情软件估计方法中的EPP/Spectrum软件于2007年亦引入贝叶斯统计,对EPP中4个参数(流行开始年份t0,感染强度r,行为调整参数φ,流行初期易感者在成年人中所占的比例f0)进行估计,其先验信息服从均匀分布,使得贝叶斯统计在疫情估计中应用范围进一步扩大[26-27]。
(2)国内研究现状:贝叶斯统计在我国艾滋病疫情估计中的原创性研究相对较少,其应用主要是借鉴国外已有的贝叶斯统计方法估计疫情。李爱华等[28]利用贝叶斯基本原理推断每年新发感染人数在历年诊断发现中所占比例,并结合首次CD4检测结果反向估计出云南省德宏傣族景颇族自治州(德宏州)全州的艾滋病疫情自2008年开始呈下降趋势,诊断发现率为87.7%;同时,基于贝叶斯参数估计的EPP/Spectrum模型也广泛应用于省级乃至全国的疫情估计,并对估计的新发感染者数和死亡数进行综合评估[29-30]。
3.贝叶斯统计在艾滋病疫情估计中的应用:
贝叶斯统计由于将难以测量的参数看作随机变量而非常数,在艾滋病疫情参数不确定性估计过程中(如CD4变化规律、HIV感染后的生存和死亡规律,监测数据变化趋势的再抽样和偏差估计等)更具有优势,但很少直接用于艾滋病疫情数据(如现存活人数、死亡人数以及新发感染者数)的估计,一般多联合其他疫情估计方法如反向计算法[31-32]、动力学模型[33]、离散时间多状态模型[34]、多水平模型[23, 25]等进行疫情估计,并对模型中难以测量的参数进行不确定性估计,而参数先验分布的选取又是贝叶斯统计推断的关键,其应用包括以下几个方面:
(1)反向计算法中的贝叶斯估计:
反向计算法主要是根据艾滋病病例报告数和每年HIV感染发展为艾滋病(潜伏期)的时间分布,反推每年HIV新发感染者数量[35];贝叶斯方法应用于反向计算法主要见于Commenges和Etcheverry[12]和Wild等[15]于1993年对美国艾滋病流行初期的发病密度和发病率的估计,当艾滋病的潜伏期服从泊松分布(Piossion distribution)时,采用随机过程模型拟合艾滋病的自然疾病进程,并利用概率密度函数对泊松分布中均值参数λ进行估计,进一步通过MCMC法计算发病率的后验均值分布;随着抗病毒治疗的实施及推广,艾滋病的自然疾病进程被打破,国外学者采用生存比例函数拟合HIV感染后、治疗前的生存死亡规律变化或者采用马尔科夫模型拟合抗病毒治疗前的CD4变化规律,替代原有的简单密度函数拟合艾滋病潜伏时间概率分布[17, 36],从而改进了反向计算法。
在反向计算法中,先验信息主要是对艾滋病潜伏期分布的认知,多来源于文献、历史监测资料以及专家意见等[31],并根据先验信息确定艾滋病潜伏期的先验分布,从而在贝叶斯定理的基础上对潜伏期中难以测量的参数进行估计。Heisterkam等[37]应用贝叶斯反向计算法于1999年估计法国3类高危人群(MSM、注射吸毒人群、异性性传播人群)1981-1999年HIV发病率,其潜伏期采用随机过程拟合,根据文献资料确定其先验分布服从Poission分布,采用经验贝叶斯方法对Poission分布中的均值参数λ进行估计。
Heisterkamp等[38]于2008年再次应用反向估计法估算荷兰3类高危人群的新发感染数,与前期研究不同在于此次研究采用生存比例函数去拟合抗病毒治疗前的生存死亡变化规律,减小了抗病毒治疗对疾病进程的影响。An等[39]应用贝叶斯方法基于历年AIDS诊断数据估计美国1985-2010年的检测率与发病率间的依存关系,由于涉及两个未知变量的估计,采用分层贝叶斯方法将其划分为两个层次进行估计,并根据历年的AIDS监测数据作为先验信息确定发病率服从Piossion分布,检测率服从伽马分布(Gamma distribution),其中Poission分布中的均值参数λ作为超参数是分层贝叶斯建模的基础,从而有效地解释了发病率与检测率的相关性。
(2)离散时间多状态模型中的贝叶斯估计:
离散时间多状态模型是基于马尔科夫(Markov)原理,将HIV感染到首次诊断(HIV或AIDS状态)的疾病进程按照CD4水平不同划分为不同状态,并根据疾病诊断状态估计HIV新发感染者数的一种疫情估计方法[19];模型参数主要包括了HIV新发感染人数的对数γi、诊断概率di,k和不同CD4状态之间的转移概率qk,k+1,模型中涉及到的先验分布常根据模型中参数的不同而存在差异,其中新发感染人数的对数γi服从正态先验分布,由于新发感染人数往往是未知的,且对γi无任何先验信息,故常采用无信息先验确定其先验分布;诊断概率di,k服从Beta分布,其先验分布来源于新近诊断的HIV/AIDS首次CD4值,但在艾滋病早期监测中,由于CD4值没有被测量,在无CD4值的情况下,对于诊断概率先验信息的选取时,文献资料也是其来源之一[40];值得注意的是,对于不同CD4状态下的转移概率qk,k+1的计算,一般是引用已发表的队列研究结果,作为先验信息应用于多状态模型,符合贝叶斯统计思想[19];对参数的估计尽管有学者使用惩罚似然方法进行诊断概率的估计,但未曾考虑数据漏报的情况[41],而采用贝叶斯方法能够利用先验信息对难以测量参数进行估计,从而完成艾滋病疫情评估;Sweeting等[18]于2005年使用离散时间多状态模型结合贝叶斯方法估计英格兰和威尔士1981-2003年MSM人群中HIV新发感染者数,并以一个季度为时间间隔单位,将历年新诊断病例最近的CD4值作为季度诊断概率di,k的先验信息,采用经验贝叶斯方法通过MCMC算法模拟计算诊断概率,进一步得到HIV新发感染者数;Birrell等[42]则引入分层贝叶斯方法估计离散多状态模型中诊断概率,并使用随机游走过程绘制出英格兰和威尔士1978-2010年MSM人群的发病率和诊断率平滑曲线。此研究中诊断概率采用的先验来源于已发表的文献资料,并且纳入多状态模型的数据是连续多次CD4检测的首次记录,避免了将HIV感染初期CD4急剧下降错分为长期感染的可能性,减小对新发感染人数估计的影响。Brizzi等[34]利用离散时间多状态模型于2019年再次对英格兰和威尔士MSM人群不同年龄组的HIV发病率进行估计,并将CD4值作为诊断概率的先验信息,探讨年龄与诊断概率的依存关系。
(3)动力学模型中的贝叶斯估计:
动力学模型主要是根据疾病的发生、发展、传播规律以及环境变化情况等构建能够反映传染病动力学特性的数学模型,并通过模型模拟疾病的传播过程,反映疾病的传播规律和发展趋势[43];模型基本参数有传染率系数(β),移除比例系数(γ),基本再生率(R0)。在动力学模型中这些参数往往是难以测量的,对于参数的估计尽管可以采用经典统计学中的线性或非线性回归方法,但其随机误差分布假设一般为正态分布,这与艾滋病的实际数据存在一定的偏性不相符,基于模型正态性假设的统计推断可能会导致错误的估计结果[21];因此使用经典统计学方法对模型参数的估计有待改进,而对于模型多个参数之间相关性的估计,分层贝叶斯方法在处理这种参数相关性方面更具有优势[44];Dale和Guo[45]利用分层贝叶斯方法对美国HIV诊断比例随机变化情况进行参数估计,传染率系数β先验信息的选取来自于美国CDC 2014年的HIV监测数据,其先验分布服从Gamma分布,结果显示HIV诊断比例从2005年的78%上升至2013年的84%,进一步估计出HIV传染率为3.4%,但此模型未考虑到移除率对HIV传播力的影响。
动力学模型中采用分层贝叶斯方法对多个参数进行估计,其先验分布较为复杂;其中,先验分布中含有的未知参数称之为超参数,对超参数再作一个先验分布,称之为超先验分布,由先验分布和超先验分布共同组成分层贝叶斯方法的分层先验,从而解决艾滋病动力学模型中的多参数估计问题[46];因此,动力学模型中的参数估计最主要的是利用先验信息确定先验分布,以便在贝叶斯框架下进行后验分布的推断;Huang等[33]基于动力学模型中HIV纵向数据按照个体内以及个体间分两层对模型参数进行贝叶斯估计,选取已发表的文献研究作为分层贝叶斯方法中参数估计的先验信息,结合HIV临床试验数据进行统计推断;Vesga等[47]基于无信息先验提出确定性模型,在贝叶斯框架下对哥伦比亚HIV发病率进行估计,其先验分布服从均匀分布U(0~1);Ushakova等[46]将分层贝叶斯方法应用于CD4重复测量的数据进行参数估计,其先验信息来源于文献、监测数据以及无信息先验,综合先验信息与抽样信息,对动力学模型诸多参数进行不确定性估计,并对后验分布的计算采用MCMC算法,已成为动力学模型估计艾滋病疫情中较为常用的参数估计方法。
(4)多水平模型中的贝叶斯估计:
在艾滋病监测数据中,CD4值和病毒载量的重复测量形成了一系列的纵向数据,利用多水平模型(混合效应模型)中线性或非线性模型拟合CD4值或者病毒载量随时间变化有助于了解疾病进程[48],但实际应用中,此类数据往往是呈偏态分布且数据之间不存在独立性,不满足线性回归成立条件,故采用一般的线性回归模型难以反映不同测量个体之间以及不同测量次数之间的混合效应(包括固定效应和随机效应)[49],因此常利用多水平模型拟合CD4和病毒载量的变化规律,并利用贝叶斯统计对随机斜率与截距进行估计[23, 50]。Lange等[13]利用旧金山327名受试者的CD4纵向检测数据应用非线性随机效应模型预测CD4递减规律,并按照不同测量个体之间以及不同测量次数之间分两层对随机斜率与截距进行贝叶斯分层估计;Lu和Huang[24]应用线性混合效应模型拟合病毒载量和CD4水平随时间变化情况,对混合效应模型的随机斜率与截距进行贝叶斯估计。
由于多水平模型在拟合CD4或者病毒载量随时间变化的过程中存在重复测量的问题,因此常利用分层贝叶斯方法探求水平1(同一个体不同测量次数)与水平2(不同个体)之间的混合效应,且对于模型不同个体之间的随机效应进行参数估计,但由于拟合过程中数据呈线性或非线性特征,先验信息选取不同导致先验分布也存在差异;其中非线性随机效应模型中的先验分布服从于正态分布(Normal distributions),先验信息常来自于文献资料[13, 22];线性混合效应模型则用于更为复杂的参数计算,一般采用分层贝叶斯方法处理多水平模型不同层次之间的混合效应,其中各层次中超先验分布服从多种参数分布,如指数分布、Beta分布、Gamma分布以及Jeffrey独立先验分布等[24],而鉴于诸多参数估计存在一定困难,也可采用半参数或非参数贝叶斯模型进行参数估计,减小复杂参数估计中的误差[20, 51]。
4.贝叶斯统计应用注意事项:
尽管国外对于贝叶斯统计在艾滋病疫情估计中的应用较为广泛,但国内研究尚处于起步阶段,因此,在疫情估计中的应用需要注意以下几个问题:
(1)先验分布的选取:先验信息的选取是确定贝叶斯统计先验分布的前提,是人们在抽样前对所求参数的主观认知;在艾滋病疫情估计中,先验信息的来源可以是CD4监测数据、文献资料以及专家意见;对一些确实缺少历史资料的参数估计,亦可采用无信息先验估计,其分布常服从均匀分布U(0~1)[47]。
(2)贝叶斯方法的选择:艾滋病疫情估计方法或模型往往涉及到多个不同参数,基于不同的先验信息对难测量参数进行估计需选择合适的贝叶斯方法;经验贝叶斯方法适合于有历史样本数据或文献资料作为先验信息的估计[38],如离散时间多状态模型中的诊断概率计算;分层贝叶斯方法则适用于多层次之间不同参数相关性的分层估计,如动力学模型和多水平模型中多参数的估计等,此类情况往往不能一步给出先验信息的参数估计,采用分层贝叶斯方法能够减少相应的误差,使估计结果更加接近真实疫情[52]。
(3)计算编程问题:艾滋病疫情估计中通过贝叶斯定理对难以测量参数进行后验分布的计算多采用MCMC算法,可利用R软件包、WinBUGS等软件实现,但由于艾滋病疫情估计方法的选择不同,导致应用贝叶斯统计时计算机编程也不一样,缺乏一定的系统性[53];若能对MCMC算法在艾滋病疫情估计中计算机编程形成统一的认识,将会大大地促进贝叶斯统计在艾滋病疫情估计中的应用。
5.总结与展望:
贝叶斯统计在艾滋病疫情估计中的应用也处于不断探索的阶段,而利用贝叶斯统计的优势在于其能够很好地与其他疫情估计方法相结合,将多种来源的信息以及未知参数的不确定性估计,通过贝叶斯定理整合在一个框架里,选择更为恰当的先验分布能够提高疫情估计的准确性以及结果的可解释性,有助于艾滋病疫情的综合评估。未来我国艾滋病疫情估计中,应用贝叶斯统计思想对其他疫情估计方法中参数进行不确定性估计,可利用国内关于艾滋病相关研究资料作为先验信息,确定参数取值,从而使得EPP/Spectrum等软件的参数本土化,使之更加适合于中国的艾滋病疫情估计。同时,对于监测数据缺乏的地区,利用贝叶斯统计中的先验信息补充数据缺失带来的影响,从而估计出小区域范围内的疫情,也将是未来疫情估计中值得探讨的方向。
利益冲突 所有作者均声明不存在利益冲突
| [1] |
Cousins MM, Konikoff J, Laeyendecker O, et al. HIV diversity as a biomarker for HIV incidence estimation:including a high-resolution melting diversity assay in a multiassay algorithm[J]. J Clin Microbiol, 2014, 52(1): 115-121. DOI:10.1128/JCM.02040-13 |
| [2] |
Jenniskens F, Tiendrebeogo G, Coolen A, et al. How countries cope with competing demands and expectations:perspectives of different stakeholders on priority setting and resource allocation for health in the era of HIV and AIDS[J]. BMC Public Health, 2012, 12: 1071. DOI:10.1186/1471-2458-12-1071 |
| [3] |
唐林, 孙坤, 陈方方, 等. 艾滋病疫情估计与预测方法研究进展[J]. 中华流行病学杂志, 2019, 40(6): 731-738. Tang L, Sun K, Chen FF, et al. Progress on estimation and projection of HIV epidemics[J]. Chin J Epidemiol, 2019, 40(6): 731-738. DOI:10.3760/cma.j.issn.0254-6450.2019.06.024 |
| [4] |
Mahy M, Brown T, Stover J, et al. Producing HIV estimates:from global advocacy to country planning and impact measurement[J]. Glob Health Action, 2017, 10(Suppl 1): 1291169. DOI:10.1080/16549716.2017.1291169 |
| [5] |
茆诗松, 汤银才. 贝叶斯统计[M]. 2版. 北京: 中国统计出版社, 2012. Mao SS, Tang YC. Bayesian statistics[M]. 2nd ed. Beijing: China Statistics Press, 2012. |
| [6] |
韩明. 贝叶斯统计学及其应用[M]. 上海: 同济大学出版社, 2015. Han M. Bayesian statistics and its applications[M]. Shanghai: Tongji University Press, 2015. |
| [7] |
Apenteng OO, Ismail NA. A markov chain monte carlo approach to estimate AIDS after HIV infection[J]. PLoS One, 2015, 10(7): e0131950. DOI:10.1371/journal.pone.0131950 |
| [8] |
Robert C, Ntzoufras I. Bayesian modeling using WinBUGS[J]. CHANCE, 2012, 25(2): 60-61. DOI:10.1080/09332480.2012.685377 |
| [9] |
Ashby D. Bayesian statistics in medicine:a 25 years review[J]. Stat Med, 2006, 25(21): 3589-3631. DOI:10.1002/sim.2672 |
| [10] |
Taylor JMG. Models for the HIV infection and AIDS epidemic in the United States[J]. Stat Med, 1989, 8(1): 45-58. DOI:10.1002/sim.4780080107 |
| [11] |
Zeger SL, See LC, Diggle PJ. Statistical methods for monitoring the AIDS epidemic[J]. Stat Med, 1989, 8(1): 3-21. DOI:10.1002/sim.4780080104 |
| [12] |
Commenges D, Etcheverry B. An empirical Bayes approach to the estimation of the incidence curve of HIV infection[J]. Stat Med, 1993, 12(14): 1317-1324. DOI:10.1002/sim.4780121404 |
| [13] |
Lange N, Carlin BP, Gelfand AE. Hierarchical bayes models for the progression of HIV infection using longitudinal CD+4 T-Cell numbers[J]. J Am Stat Assoc, 1992, 87(419): 615-626. DOI:10.1080/01621459.1992.10475258 |
| [14] |
Raab GM, Gore SM, Goldberg DJ, et al. Bayesian forecasting of the human immunodeficiency virus epidemic in scotland[J]. J Roy Stat Soc, Ser A (Stat in Soc), 1994, 157(1): 17-30. DOI:10.2307/2983502 |
| [15] |
Wild P, Commenges D, Etcheverry B. A hierarchical bayesian approach to the back-calculation of numbers of HIV-infected subjects[J]. J Roy Stat Soc, Ser D (Stat), 1993, 42(4): 405-414. DOI:10.2307/2348474 |
| [16] |
Putter H, Heisterkamp SH, Lange JMA, et al. A Bayesian approach to parameter estimation in HIV dynamical models[J]. Stat Med, 2002, 21(15): 2199-2214. DOI:10.1002/sim.1211 |
| [17] |
Downs AM, Heisterkamp SH, Ravà L, et al. Back-calculation by birth cohort, incorporating age-specific disease progression, pre-AIDS mortality and change in European AIDS case definition[J]. AIDS, 2000, 14(14): 2179-2189. DOI:10.1097/00002030-200009290-00015 |
| [18] |
Sweeting MJ, de Angelis D, Aalen OO. Bayesian back-calculation using a multi-state model with application to HIV[J]. Stat Med, 2005, 24(24): 3991-4007. DOI:10.1002/sim.2432 |
| [19] |
Aalen OO, Farewell VT, de Angelis D, et al. A Markov model for HIV disease progression including the effect of HIV diagnosis and treatment:application to AIDS prediction in England and Wales[J]. Stat Med, 1997, 16(19): 2191-210. DOI:10.1002/(sici)1097-0258(19971015)16:19<2191:aid-sim645>3.0.co;2-5 |
| [20] |
Castro LM, Wang WL, Lachos VH, et al. Bayesian semiparametric modeling for HIV longitudinal data with censoring and skewness[J]. Stat Methods Med Res, 2019, 28(5): 1457-1476. DOI:10.1177/0962280218760360 |
| [21] |
李莹, 王仲君, 赵华玲. 基于贝叶斯推断的HIV非线性混合效应联合模型研究[J]. 统计研究, 2012, 29(7): 86-90. Li Y, Wang ZJ, Zhao HL. Bayesian inference for nonlinear mixed-effects joint Model in HIV study[J]. Stat Res, 2012, 29(7): 86-90. DOI:10.3969/j.issn.1002-4565.2012.07.015 |
| [22] |
Patwardhan SC, Narasimhan S, Jagadeesan P, et al. Nonlinear Bayesian state estimation:a review of recent developments[J]. Control Eng Pract, 2012, 20(10): 933-953. DOI:10.1016/j.conengprac.2012.04.003 |
| [23] |
Tian YZ, Lian H, Tian MZ. Bayesian composite quantile regression for linear mixed-effects models[J]. Commun Stat-Theory Methods, 2017, 46(15): 7717-7731. DOI:10.1080/03610926.2016.1161798 |
| [24] |
Lu T, Huang YX. Bayesian inference on mixed-effects varying-coefficient joint models with skew-t distribution for longitudinal data with multiple features[J]. Stat Methods Med Res, 2017, 26(3): 1146-1164. DOI:10.1177/0962280215569294 |
| [25] |
Huang YX, Lu T. Bayesian inference on partially linear mixed-effects joint models for longitudinal data with multiple features[J]. Comput Stat, 2017, 32(1): 179-196. DOI:10.1007/s00180-016-0671-5 |
| [26] |
Brown T, Salomon JA, Alkema L, et al. Progress and challenges in modelling country-level HIV/AIDS epidemics:the UNAIDS Estimation and Projection Package 2007[J]. Sex Transm Infect, 2008, 84(Suppl 1): i5-10. DOI:10.1136/sti.2008.030437 |
| [27] |
Alkema L, Raftery AE, Clark SJ. Probabilistic projections of HIV prevalence using Bayesian melding[J]. Ann Appl Stat, 2007, 1(1): 229-248. DOI:10.1214/07-AOAS111 |
| [28] |
李爱华, 江震, 段松, 等. 基于CD4+T淋巴细胞水平反推法估计云南省德宏傣族景颇族自治州HIV诊断发现率[J]. 中华预防医学杂志, 2018, 52(8): 833-836. Li AH, Jiang Z, Duan S, et al. Estimation of HIV diagnosis rate with CD4+ T-lymphocyte level and infected-time model in Dehong Prefecture, Yunnan province[J]. Chin J Prev Med, 2018, 52(8): 833-836. DOI:10.3760/cma.j.issn.0253-9624.2018.08.011 |
| [29] |
卢飞豹, 廖清华, 胡国良, 等. Spectrum模型在江西省艾滋病疫情估计与预测中的应用[J]. 中国艾滋病性病, 2015, 21(3): 220-222. Lu FB, Liao QH, Hu GL, et al. Application of Spectrum model in estimation, prediction and analysis on the HIV/AIDS epidemic of Jiangxi province[J]. Chin J AIDS STD, 2015, 21(3): 220-222. DOI:10.13419/j.cnki.aids.2015.03.14 |
| [30] |
中华人民共和国卫生部, 联合国艾滋病规划署, 世界卫生组织. 2011年中国艾滋病疫情估计[J]. 中国艾滋病性病, 2012, 18(1): 1-5. Ministry of Health of the People's Republic of China, UNAIDS, World Health Organization. Estimation of AIDS epidemic in China in 2011[J]. Chin J AIDS STD, 2012, 18(1): 1-5. DOI:10.13419/j.cnki.aids.2012.01.005 |
| [31] |
Ventura L, Mezzetti M. Estimating cancer incidence using a Bayesian back-calculation approach[J]. Stat Med, 2014, 33(25): 4453-4468. DOI:10.1002/sim.6240 |
| [32] |
Crump RE, Medley GF. Back-calculating the incidence of infection of leprosy in a Bayesian framework[J]. Parasit Vectors, 2015, 8: 534. DOI:10.1186/s13071-015-1142-5 |
| [33] |
Huang YX, Liu DC, Wu HL. Hierarchical Bayesian methods for estimation of parameters in a longitudinal HIV dynamic system[J]. Biometrics, 2006, 62(2): 413-423. DOI:10.1111/j.1541-0420.2005.00447.x |
| [34] |
Brizzi F, Birrell PJ, Plummer MT, et al. Extending Bayesian back-calculation to estimate age and time specific HIV incidence[J]. Lifetime Data Anal, 2019, 25(4): 757-780. DOI:10.1007/s10985-019-09465-1 |
| [35] |
Wong NS, Wong KH, Lee MP, et al. Estimation of the undiagnosed intervals of HIV-infected individuals by a modified back-calculation method for reconstructing the epidemic curves[J]. PLoS One, 2016, 11(7): e0159021. DOI:10.1371/journal.pone.0159021 |
| [36] |
Hendriks JC, Satten GA, Longini IM, et al. Use of immunological markers and continuous-time Markov models to estimate progression of HIV infection in homosexual men[J]. AIDS, 1996, 10(6): 649-656. DOI:10.1097/00002030-199606000-00011 |
| [37] |
Heisterkam SH, van Houwelingen JC, Downs AM. Empirical Bayesian estimators for a poisson process propagated in time[J]. Biom J, 1999, 41(4): 385-400. DOI:10.1002/(SICI)1521-4036(199907)41:4<385::AID-BIMJ385>3.0.CO;2-Z |
| [38] |
Heisterkamp SH, de Vries R, Sprenger HG, et al. Estimation and prediction of the HIV-AIDS-epidemic under conditions of HAART using mixtures of incubation time distributions[J]. Stat Med, 2008, 27(6): 781-794. DOI:10.1002/sim.2974 |
| [39] |
An Q, Kang J, Song RG, et al. A Bayesian hierarchical model with novel prior specifications for estimating HIV testing rates[J]. Stat Med, 2016, 35(9): 1471-1487. DOI:10.1002/sim.6795 |
| [40] |
Nuñez O, Hernando V, Díaz A. Estimating the number of people living with HIV and the undiagnosed fraction in Spain in 2013[J]. AIDS, 2018, 32(17): 2573-2581. DOI:10.1097/qad.0000000000001989 |
| [41] |
Sommen C, Alioum A, Commenges D. A multistate approach for estimating the incidence of human immunodeficiency virus by using HIV and AIDS French surveillance data[J]. Stat Med, 2009, 28(11): 1554-1568. DOI:10.1002/sim.3570 |
| [42] |
Birrell PJ, Chadborn TR, Gill ON, et al. Estimating trends in incidence, time-to-diagnosis and undiagnosed prevalence using a CD4-based Bayesian back-calculation[J]. Stat Commun Infect Dis, 2012, 4(1). DOI:10.1515/1948-4690.1055 |
| [43] |
Hethcote HW. The mathematics of infectious diseases[J]. SIAM Rev, 2000, 42(4): 599-653. DOI:10.1137/S0036144500371907 |
| [44] |
Huang YX, Dagne GA. Simultaneous Bayesian inference for skew-normal semiparametric nonlinear mixed-effects models with covariate measurement errors[J]. Bayesian Anal, 2012, 7(1): 189-210. DOI:10.1214/12-BA706 |
| [45] |
Dale R, Guo BB. Estimating epidemiological parameters of a stochastic differential model of HIV dynamics using hierarchical Bayesian statistics[J]. PLoS One, 2018, 13(7): e0200126. DOI:10.1371/journal.pone.0200126 |
| [46] |
Ushakova A, Pettersen FO, Maeland A, et al. Bayesian estimation of HIV-1 dynamics in vivo[J]. Math Med Biol, 2015, 32(1): 39-56. DOI:10.1093/imammb/dqt018 |
| [47] |
Vesga JF, Cori A, van Sighem A, et al. Estimating HIV incidence from case-report data:method and an application in Colombia[J]. AIDS, 2014, 28(Suppl 4): S489-496. DOI:10.1097/QAD.0000000000000466 |
| [48] |
Tilling K, Lawton M, Robertson N, et al. Modelling disease progression in relapsing-remitting onset multiple sclerosis using multilevel models applied to longitudinal data from two natural history cohorts and one treated cohort[J]. Health Technol Assess, 2016, 20(81): 1-48. DOI:10.3310/hta20810 |
| [49] |
Huang YX, Chen R, Dagne G. Simultaneous Bayesian inference for linear, nonlinear and semiparametric mixed-effects models with skew-normality and measurement errors in covariates[J]. Int J Biostat, 2011, 7(1): 8. DOI:10.2202/1557-4679.1292 |
| [50] |
Lodi S, Phillips A, Touloumi G, et al. Time from human immunodeficiency virus seroconversion to reaching CD4+ cell count thresholds < 200, < 350, and < 500 Cells/mm3:assessment of need following changes in treatment guidelines[J]. Clin Infect Dis, 2011, 53(8): 817-825. DOI:10.1093/cid/cir494 |
| [51] |
Sinha S, Wang SJ. Semiparametric Bayesian analysis of censored linear regression with errors-in-covariates[J]. Stat Methods Med Res, 2017, 26(3): 1389-1415. DOI:10.1177/0962280215580668 |
| [52] |
Romero-Severson EO, Lee Petrie C, Ionides E, et al. Trends of HIV-1 incidence with credible intervals in Sweden 2002-09 reconstructed using a dynamic model of within-patient IgG growth[J]. Int J Epidemiol, 2015, 44(3): 998-1006. DOI:10.1093/ije/dyv034 |
| [53] |
Nama R, Vijaya AK, Guptan R, et al. Bayesian approach of reliability parameter estimation using WinBUGS[C]//Proceedings of 20102nd international conference on reliability, safety and hazard-risk-based technologies and physics-of-failure methods. Mumbai, India: IEEE, 2010: 147-150. DOI: 10.1109/ICRESH.2010.5779533.
|
 2020, Vol. 41
2020, Vol. 41


