文章信息
- 王小磊, 田梦圆, 张娜, 高红, 谭红专.
- Wang Xiaolei, Tian Mengyuan, Zhang Na, Gao Hong, Tan Hongzhuan
- 纵向数据中评估暴露总效应的序列条件平均模型
- A sequential conditional mean model for assessing total effects of exposure in longitudinal data
- 中华流行病学杂志, 2020, 41(1): 111-114
- Chinese Journal of Epidemiology, 2020, 41(1): 111-114
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2020.01.020
-
文章历史
收稿日期: 2019-06-19
2. 湖南省人民医院/湖南师范大学附属第一医院, 长沙 410016
2. Hunan Provincial People's Hospital/the First Affiliated Hospital of Hunan Normal University, Changsha 410016, China
在有重复测量的纵向研究中,对暴露与结局之间的因果效应进行估计是现代流行病学研究中一个常见的问题。该类研究方法的一个显著特点是需要对研究对象进行多次随访,每个个体经过多次随访会产生多个相互关联的观测值,且每次随访时暴露和结局都可能会随时间发生变化,该类暴露被称为时依性暴露。在估计时依性暴露的效应时可能会受到时依性混杂因素的影响,该混杂因素满足的3个条件:①随时间变化的变量;②该变量是结局的影响因素;③该变量既影响到随后的暴露同时又会受到先前暴露的影响[1-2]。由于该类数据存在各个观测值之间相互关联,所以直接采用传统的多因素回归模型对其分析可能会忽视组内相关从而产生偏倚。
Robins等[1]在1999年提出了边缘结构模型(marginal structural models,MSM),该模型作为一种可以处理时依性混杂的方法而被广泛应用。其原理是通过计算逆概率权重对原人群进行加权从而构造出虚拟人群,在该虚拟人群中对暴露总效应进行评估[3-4]。但是,在对原人群进行加权时,由于某些个体协变量差异过大而导致极端权重的出现,如果直接对极端权重进行截断又可能导致某些重要信息缺失,在小样本中该暴露总效应的评估可能会存在偏倚[5]。同时,在暴露和非暴露前一阶段的协变量差异很大时,MSM估计的边际效应可能不能真实的反映暴露的总效应。
本文将介绍另一种可以处理时依性混杂的新方法——序列条件平均模型(sequential conditional mean models,SCMM)。该方法是Keogh等[6]在2017年提出的,是在传统回归方法的基础上发展起来的,与传统回归方法相比,其主要区别是将过去的暴露、结果作为时依性混杂因素纳入模型中进行校正。并且广义估计方程(generalized estimating equation,GEE)的发展与完善,为SCMM模型参数的估计提供前提条件。下文将介绍如何使用SCMM对二分类暴露与连续性结果之间的总体效应进行评估,并对SCMM的原理、暴露总效应评估过程、SCMM的适用条件及优缺点进行概述。
一、基本原理在重复测量的纵向研究中,对研究对象进行T次随访,t=1,…,T,在t次随访上观测其暴露(Xt)、结局(Yt)以及时依性协变量(Lt),其中Xt代表[t-1,t)期间的暴露状态、Yt代表(t,t+1]期间的结局。Ux、UY分别表示影响暴露和结局未观测到的不可测量的随机效应。
如因果路径图所示:Xt受到前一阶段的暴露(Xt-1)、前一阶段的结局(Yt-1)、时依性混杂协变量(Lt)的影响,并且每次随访时测量的Xt均会发生变化。同时Yt-1也受到Xt-1和Lt-1的影响,并对Xt、Yt产生影响,即Yt-1可以被看作影响Xt与Yt之间因果关系的时依性混杂因素。暴露对结局的总效应可以分解为包含未来暴露的间接暴露效应和不包含未来暴露的直接暴露效应,例如Xt-1对Yt的暴露总效应可以分解为直接暴露途径Xt-1→Lt→Yt、Xt-1→Yt和间接暴露途径Xt-1→Xt→Yt、Xt-1→Lt→Xt→Yt。
在SCMM中,采用标准回归方法将Xt-1、Yt-1以及Lt纳入模型中,通过模型对这些具有混杂作用的协变量进行校正,从而对Xt与Yt之间暴露总效应进行无偏的估计。该模型主要对二分类暴露与连续性结局之间的暴露总效应进行估计,不能对某种特定暴露模式的联合效应进行评估[6]。
二、暴露总效应的估计1. Xt对Yt的总效应评估模型:首先,为Yt拟合一个模型,假设不存在UY,即Yt仅受到Xt、Xt-1、Lt的影响,同时Yt-1对Xt的暴露效应也会产生影响[7],采用模型(1)可以对暴露总效应进行评估,βx1代表Xt与Yt之间的总体效应,模型(1)即SCMM。
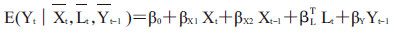 (1)
(1)
2. Xt-a对Yt的总效应评估模型:在模型(1)的基础上,将交互项、基线协变量以及与时间有交互作用的协变量均拟合进模型中,模型(1)可以直接拓展成模型(2),模型(2)可用于评价Xt-a(a=1,2,…,)的总暴露效应。βX1代表Xt-a与Yt之间的总效应。
 (2)
(2)
3.纳入倾向评分的模型:倾向评分(propensityscore,PS)指在一定协变量的情况下,某个研究对象接受暴露的可能性大小,即
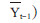
如图 1所示:某研究对象在时间t上的暴露Xt的影响因素包括Xt-1、Lt以及Yt-1。即建立Xt与Xt-1、Yt-1、Lt的logistic回归模型。
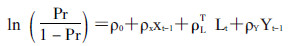 (3)
(3)
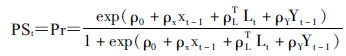 (4)
(4)
 (5)
(5)

|
| 图 1 因果路径图 |
模型(3)、(4)是对某个研究类似的将PS看作是Xt-1、Lt、Yt-1所产生混杂作用的综合。模型(5)是通过将PS作为特殊的混杂因子纳入模型(1)中进行校正所形成的PS模型。将PS纳入模型中,对于模型的稳定程度以及估计精度都有提高,只要模型(1)或模型(5)是正确设立的(即依据上述的原理图,理清各变量之间的关系),在大样本条件下,线性模型就可以无偏且比较稳健地估计暴露效应βX1。此外,对于那些很难找到同质可比的非暴露个体的暴露个体,该方法可以降低其权重,使其在没有较好同质性的对照人群下,仍可以较好地估计暴露的效应[10-11]。
4. SCMM的参数估计:SCMM的参数估计可以看作是GEE的解。GEE是在广义线性模型的基础上发展起来可以对具有组内相关性的纵向数据进行分析,其要求不同观察对象之间的观测值相互独立,允许同一受试者多次观测值之间存在组内相关。但是,GEE只有在不存在UY以及Yt-1独立于Xt、Lt的情况下才可以对参数进行无偏估计,否则可能会产生偏倚(GEE偏倚)。为了克服这种偏倚,SCMM将Yt-1纳入模型中进行校正来避免这种偏倚。
SCMM的参数就是解释变量的系数β,该参数的确切估计依赖于Ø和α,只有在给定确切的Ø和α估计值后,才能对β进行无偏估计。其中的Ø是离散参数,其确切估计依赖于结局变量的分布类型,在统计软件中体现于连接函数的正确选择;α是相关系数参数,其确切估计值依赖于作业相关矩阵的选择[12]。所以在进行统计软件分析时需要对连接函数和工作相关矩阵做出正确选择。首先,连接函数的选择依赖于结局变量的分布类型,例如结局变量是满足高斯分布的连续性变量,其连接函数选择恒等函数、满足伯努利分布或者二项分布的二分类变量时选择logit函数、满足泊松分布的计数资料选择log函数。其次是需要选择正确的作业相关矩阵,常见的几种可以解释重复测量间相关性的作业相关矩阵形式主要有可交换相关、独立相关、不确定型相关、自相关、相邻相关等[13]。其选择的方法有两种,第一种是根据数据资料的特点,例如对于重复测量等具有时间顺序特点的资料可以采用自相关和相邻相关、对于测量间无时间顺序关系的资料采用可交换相关、难以确定相关结构的采用不确定型相关[14]。同时,如果在实际操作中没有确定作业相关矩阵,软件初始默认采用独立作业相关矩阵,其在迭代运算中自动对矩阵进行更新。第二种方法是针对数据本身的特点,通过准似然独立准则(Quasi-Likelihood under Independence Model Criterion,QIC)对模型进行判定[14-15],该准则不仅可以用于作业相关矩阵的选择,还可以用于协变量的筛检从而对模型进行优化,该方法可以直接在统计软件中操作,其判断的标准是其统计量的估计值,其值越小说明模型拟合越好。
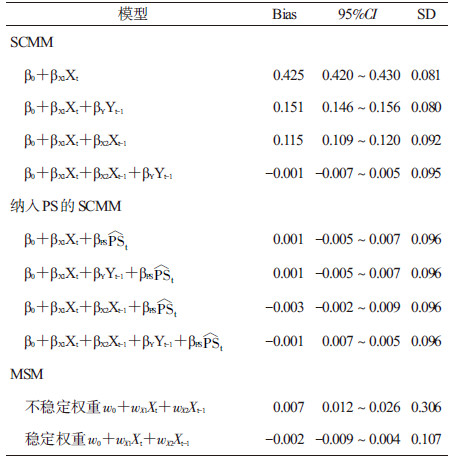
三、模拟研究Keogh等[6]利用一个假设的“200例个体随访5次”的随机数据,利用模型进行模拟研究。将单个模拟数据集的生成过程重复1 000次,形成1 000个模拟数据集并分别用SCMM、MSM对暴露的总效应进行估计。对同一模型估计效应时所产生的1 000个偏倚进行统计分析,包括偏倚的估计值(Bias)、95%CI、标准差(s),应用这些统计指标对不同模型进行比较。
模拟结果提示,在完全没有考虑时依性混杂因素(如Xt-1、Yt-1)时(SCMM模型1),其偏倚达到0.425,随着将时依性混杂因素加入调整模型中(SCMM模型2加入了Xt-1,SCMM模型3加入了Yt-1),其偏倚逐渐减少,当全部时依性混杂因素都加入调整模型中时(SCMM模型4),其效应估计是无偏的,且标准差降至0.095。在纳入PS的SCMM中,所有模型的估计均是无偏估计,即纳入PS可以提升SCMM模型控制偏倚的效果。虽然MSM在权重稳定时也可以对暴露效应进行无偏估计,但其标准差大于SCMM,即在估计效应的稳定性方面不如SCMM;而在权重不稳定时,MSM模型还是不能完全控制偏倚。
四、小结对于具有组内相关性的纵向数据,采用传统的多因素回归方法分析这类数据时由于无法解决时依性混杂因素而产生偏倚。SCMM是分析这类数据的一种新方法,该方法是在传统回归的基础上将时依性混杂因素纳入模型中进行校正从而对纵向数据中暴露与结局的效应进行无偏估计。与MSM相比,SCMM具有简单、灵活等优势,例如在拟合MSM时,需要先构造虚拟人群并且由于可能存在差异较大的协变量,在构造逆概率权重时可能需要注意极端权重的出现,所以MSM的拟合相对于SCMM更加复杂。同时在交互作用处理方面,MSM只能将基线协变量与暴露之间的交互作用通过逆概率权重的计算过程进行校正,而SCMM可以直接将暴露与时依性协变量之间的交互项纳入模型中进行校正,所以SCMM在处理交互项作用方面比MSM更加灵活。SCMM将PS纳入模型中,使得模型具有稳健性,并且SCMM还可以更容易地扩展以适应连续的暴露和删失数据[6]。SCMM也存在一些局限性,如SCMM只能估计当前单个暴露对后续结局的总效应,不能估计特定的联合暴露效应。
利益冲突 所有作者均声明不存在利益冲突
| [1] |
Robins JM, Hernán MA, Brumback B. Marginal structural models and causal inference inepidemiology[J]. Epidemiology, 2000, 11(5): 550-560. DOI:10.1097/00001648-200009000-00011 |
| [2] |
Arah OA, Sudan M, Olsen J, et al. Marginal structural models, doubly robust estimation, and bias analysis in perinatal and pediatric epidemiology[J]. Paediatr Perinat Epidemiol, 2013, 27(3): 263-265. DOI:10.1111/ppe.12049 |
| [3] |
Zheng WJ, Luo ZH, van der Laan MJ. Marginal structural models with counterfactual effect modifiers[J]. Int J Biostat, 2018, 14(1). DOI:10.1515/ijb-2018-0039 |
| [4] |
田丹平, 张敏. 边际结构模型基本原理及其应用实例介绍[J]. 中国卫生统计, 2014, 31(4): 725-728. Tian DP, Zhang M. The basic principle and application examples of marginal structure model are introduced[J]. Chin J Health Stat, 2014, 31(4): 725-728. |
| [5] |
Cole SR, Hernan MA. Constructing inverse probability weights for marginal structural models[J]. Am J Epidemiol, 2008, 168(6): 656-664. DOI:10.1093/aje/kwn164 |
| [6] |
Keogh RH, Daniel RM, van der Weele TJ, et al. Analysis of longitudinal studies with repeated outcome measures:adjusting for time-dependent confounding using conventional methods[J]. Am J Epidemiol, 2018, 187(5): 1085-1092. DOI:10.1093/aje/kwx311 |
| [7] |
Newsome SJ, Keogh RH, Daniel RM. Estimating long-term treatment effects in observational data:A comparison of the performance of different methods under real-world uncertainty[J]. Stat Med, 2018, 37(15): 2367-2390. DOI:10.1002/sim.7664 |
| [8] |
Deb S, Austin PC, Tu JV, et al. A review of propensity-score methods and their use in cardiovascular research[J]. Can J Cardiol, 2016, 32(2): 259-265. DOI:10.1016/j.cjca.2015.05.015 |
| [9] |
Lee J, Little TD. A practical guide to propensity score analysis for applied clinical research[J]. Behav Res Ther, 2017, 98: 76-90. DOI:10.1016/j.brat.2017.01.005 |
| [10] |
Vansteelandt S, Daniel RM. On regression adjustment for the propensity score[J]. Stat Med, 2014, 33(23): 4053-4072. DOI:10.1002/sim.6207 |
| [11] |
Elze MC, Gregson J, Baber U, et al. Comparison of propensity score methods and covariate adjustment:evaluation in 4 cardiovascular studies[J]. J Am Coll Cardiol, 2017, 69(3): 345-357. DOI:10.1016/j.jacc.2016.10.060 |
| [12] |
Wang YG, Fu LY. Selection of working correlation structure in generalized estimating equations[J]. Stat Med, 2017, 36(14): 2206-2219. DOI:10.1002/sim.7262 |
| [13] |
Liang KY, Zeger SL. Longitudinal data analysis using generalized linear models[J]. Biometrika, 1986, 73(1): 13-22. DOI:10.1093/biomet/73.1.13 |
| [14] |
朱玉, 王静, 何倩. 广义估计方程在SPSS统计软件中的实现[J]. 中国卫生统计, 2011, 28(2): 199-201. Zhu Y, Wang J, He Q. Implementation of generalized estimation equation in SPSS statistical software[J]. Chin J Health Stat, 2011, 28(2): 199-201. DOI:10.3969/j.issn.1002-3674.2011.02.031 |
| [15] |
冯丽云, Cui J. 纵向数据准似然独立准则在GEE模型中的应用[J]. 中国卫生统计, 2008, 25(4): 369-372. Feng LY, Cui J. Application of quasi-likelihood independence criterion in GEE analyses of longitudinal data[J]. Chin J Health Stat, 2008, 25(4): 369-372. DOI:10.3969/j.issn.1002-3674.2008.04.010 |
 2020, Vol. 41
2020, Vol. 41