文章信息
- 李洋, 于石成, 金承刚, 杨梦婕, 马学军, 王琦琦.
- Li Yang, Yu Shicheng, Jin Chenggang, Yang Mengjie, Ma Xuejun, Wang Qiqi.
- 两组中断时间序列设计及其分析方法
- Design and analysis of two groups interrupt time series
- 中华流行病学杂志, 2019, 40(9): 1159-1163
- Chinese Journal of Epidemiology, 2019, 40(9): 1159-1163
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2019.09.027
-
文章历史
收稿日期: 2019-01-07
2. 中国疾病预防控制中心流行病学办公室, 北京 102206;
3. 北京师范大学社会发展与公共政策学院 100875
2. Office of Epidemiology, Chinese Center for Disease Control and Prevention, Beijing 102206, China;
3. School of Social Development and Public Policy, Beijing Normal University, Beijing 100875, China
当考虑大规模公共卫生干预措施,如基于人群计划免疫措施的影响时,研究人员面临的有效样本是当地社区、省市或更大的单位,而可用的唯一数据通常是以群体水平进行报告诸如发病率或死亡率等。如果可以获得关于干预期间内结果变量的多个等时间间隔的观察结果,则中断时间序列分析(interrupted time-series,ITS)可以在控制干预前上升或下降的回归趋势对序列的影响下,评价干预措施的有效性[1-3]。ITS是一种广泛应用于卫生干预评价中的类实验研究设计,评价“改变”是否可归因于干预措施,对干预效果评价的统计效率可与金标准随机对照试验(randomized controlled trial,RCT)媲美[4]。
单组ITS设计通过比较干预前后的“改变”来评价干预的有效性。通常假设任何随时间变化的未测量混杂因素都在相对缓慢地变化,以便与干预引起的“改变”区分开来。这强调了如果在干预实施的时间窗口中存在多个政策转变,则需要谨慎使用单组ITS。两组ITS则可以较好处理这样的情况,主要是因为假设干预组和对照组都受到了混杂因素的相同影响[5-6]。当干预组的结果也可以与一个或多个比较组的结果进行对比时,通过允许研究人员潜在地控制混杂因素,可以进一步增强内部效度[5]。本研究将通过介绍ITS研究设计与分析思路,并结合实例详细讲述两组ITS模型原理,拟合方法及结果解释(数据及Stata代码见:https://github.com/yeli7068/two-groups-ITS)。
1.研究设计与分析思路:应用ITS评价宏观层面上大规模人群公共卫生干预措施是十分有效的。目前单组ITS已经广泛用于国内传染病疫苗干预评价[7],医院诊疗制度评价等项目评价中[8]。使用单组ITS的主要条件之一是有效干预措施实施前结果变量的改变趋势不明显或较为缓慢,同时干预实施后结果变量有显著性改变且维持一段时间[5-6]。如果在干预实施前结果变量受到混杂因素的影响,如其他可影响结果变量的政策同时存在,从而存在很强的趋势性,此时则应当谨慎使用单组ITS。针对这种情形,两组ITS则提供了有效的解决方案。
当存在影响所有群组的公共卫生政策时,两组ITS则有十分重要的应用价值。两组ITS的关键假设是当实验组未受到干预时,结果变量水平或趋势的变化被认为与对照组是相同的。换句话说,其假设潜在混杂因素同样影响治疗组和对照组。因此两组ITS的另一主要优势是能够检验实验组与对照组之间的可比性以及平衡性。如果待分析数据来自随机对照试验,那么干预前结果变量的变化趋势则应具备相似性。当下随着生活条件日益改善,个人卫生习惯不断加强,某些研究目标变量在干预前已存在相应趋势(如传染病发病率),因此使用两组ITS则可为项目评价提供新的思路。
2.模型原理与拟合方法:
(1) 单组ITS:当没有对照组存在的情况下,经典的单组ITS回归模型假设如下:
 (1)
(1)
其中Y是在等时间间隔的情况下所测量得到的结果变量;Time表示时间变量,从初始观察点计数到最后一个观察点,取值为0,1,2 ……,n-1,其中n为观测点个数;Int为哑变量,表示干预,取值为干预前均为0,干预后均为1;Post为干预后时间变量,从干预后第一个点计数到最后一个观察点,干预发生时取值为0,随后为1,以此类推。ε为残差项,表示为没有被回归方程所解释的变异。
当拟合分段线性回归模型,完成参数估计得到β0,β1,β2以及β3。其中β0为截距项,代表结果变量的初始值;β1表示为斜率,代表干预前结果变量的长期趋势;β2表示为即刻水平改变量(immediate change in level),即干预后回归方程在第一个干预点的预测值与干预前回归方程延伸至干预点的预测值之差;β3表示为斜率改变量(change in slope),即干预前后两段回归方程斜率之差(图 1)。

|
| 图 1 单组与两组ITS示意图 |
(2) 两组ITS:当存在一个或多个对照组的情况时,公式(1)的回归方程则扩展为:
 (2)
(2)
其中Group为哑变量,代表组别(如实验组或对照组),其余变量均与上述描述一致。在图 1中,β0到β3代表下面曲线(对照组)的参数估计;β4到β7则代表实验组的参数估计。进一步可解释为β4表示为干预前对照组与实验组截距项的差异;β5表示为干预前对照组与实验组斜率的差异;β6表示为干预发生时,即刻水平改变量在对照组与实验组的差异;β7表示为干预后对照组与实验组斜率改变量之间的差异。
(3) 时间序列的自相关:使用最小二乘法(ordinary least square,OLS)对线性模型进行参数估计后需检验模型是否满足线性、独立、正态和方差齐(LINE)的条件,尤其是残差是否满足正态性。大量实践表明使用ITS时,其随机误差项存在一阶自相关[AR(1)][2, 4-5, 8],即满足:
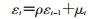 (3)
(3)
其中自相关系数ρ为相邻误差项之间的相关系数,同时满足|ρ|<1;μt服从N(0,σ2)[9]。
(4) 模型选择:当处理连续型性变量时,ITS可选择多种方法处理一阶自相关带来的影响。首先,可选择基于OLS处理自相关的参数估计方法,如广义最小二乘估计(generalized least square estimator,GLSE)进行参数估计。具体实现可使用Prais- Winsten法[10-11];此外也可以使用OLS进行参数估计,但使用Newey-West法进行标准误差的计算进而控制高阶自相关以及异方差的影响[12-14]。其次,ARIMA模型取p=1也可校正一阶自相关。如果结果变量不能很好满足线性关系,则可先进行变量转换,如对数变换、指数变换或者Box-cox变换。
ITS属于线性模型,因此也应用于广义线性模型中。在处理公共卫生领域中常见的计数型变量时,如发病数等,则可使用泊松回归模型进行ITS分析[15]。同理可见使用logit回归模型应用于分类型变量[16]。
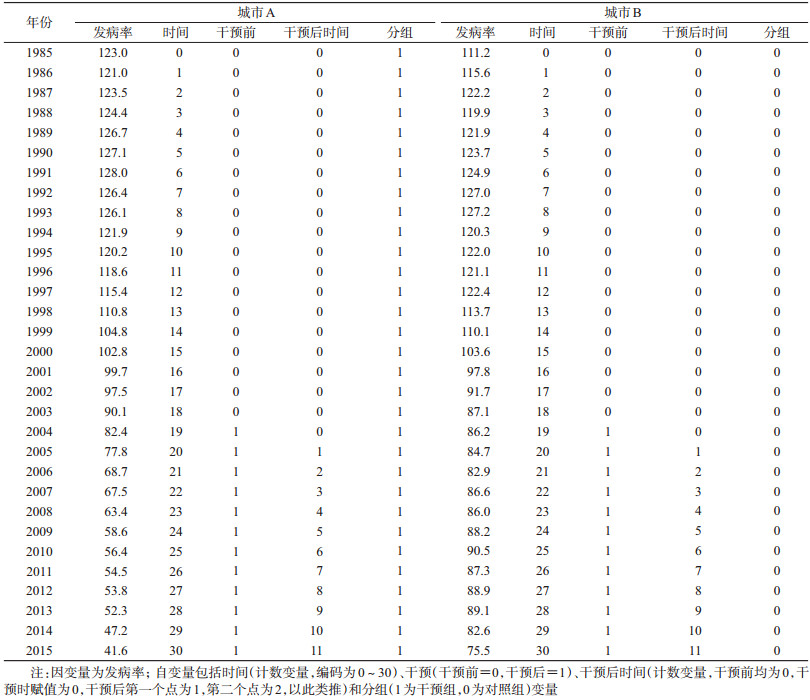
3.两组ITS应用实例:我国某地区是某急性传染病高发病率区域,近年来发病率呈下降趋势(图 2)。其中某市于2004年开始使用疫苗进行大规模干预,与之邻近的另外一个城市则未采取该措施。收集两市1985-2015年期间共30年该急性传染病发病率数据(表 1),2004年(第19个观察点)引入疫苗进行大规模干预。试探讨干预前后两市疾病发病率的变化情况。本研究假设2004年实施疫苗干预后,干预组疾病发病率可能下降(图 2)。
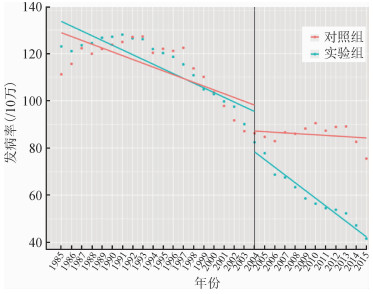
|
| 图 2 某两市疾病发病率随时间变化图 |
本研究使用Stata 15.1软件进行统计学分析。首先使用线性回归拟合模型并对模型做自相关检验(表 2)。由表 2可知,模型存在自相关,以P<0.05为阈值,可发现同时满足多种自相关阶数的备择假设。此处优先考虑一阶自相关模型,即模型自相关满足公式(3)。当处理ITS数据一阶自相关时可使用Prais-Winsten法。得到结果:
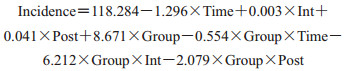
模型拟合优度检验R2为0.843,R2adj为0.823,表明拟合优度尚可。使用Durbin-Watson法对模型进行检验可以得到,当使用一般线性模型时Durbin-Watson(original)=0.452,模型存在自相关;使用Prais-Winsten法进行改善后Durbin-Watson (transformed)=1.316,序列一阶自相关虽有所改善,但改善有限。由表 2可得,该模型存在潜在高阶自相关,导致使用Prais-Winsten法改善有限。因此可考虑使用Newey-West法进行标准误差的计算进而控制潜在高阶自相关与异方差的影响,同时使用Shaprio-wilk对模型残差进行正态性检验。结果如下:
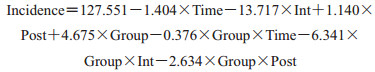
模型拟合优度检验R2为0.938,R2adj为0.930,均优于Prais-Winsten法所得结果。此外,模型残差正态性检验结果P=0.181,即接受模型残差服从正态分布的原假设。其中β0=127.551为干预前对照组截距项,代表对照组发病率的初始值,β4=1.140为干预前对照组与实验组截距项的差异(P=0.517)。结果表明在干预前,对照组与实验组之间截距项的差异无统计学意义。β1=-1.404为干预前对照组斜率,β5=-0.376为干预组与实验组斜率之差(P=0.596),表明两市在干预前发病率趋势相近,同时也用来计算疫苗干预效应时平衡干预前已存在的趋势。因此,两者之间的比较更具实际意义。
β3=1.140为干预后对照组斜率改变量,β7=-2.634为干预后对照组与实验组斜率改变量之差(P=0.004),为干预后的长期趋势变化,表明疫苗干预后使得实验组发病率发生了进一步下降,对比对照组的下降趋势有统计学意义。
β2=-13.717为对照组在干预时的即刻水平改变量,β6=-6.341为疫苗干预发生时,即刻水平改变量在对照组与实验组的差异(P=0.454)。值得注意的是,对比使用Prais-Winsten法的结果β2=0.003,即表明在干预同时发病率增加了0.003,可见当Prais-Winsten法校正一阶自相关效果较差时,会引起截然不同的结果(图 2)。
4.讨论:单组ITS在没有对照的情况下,控制时间序列在干预前已有的上升或下降趋势,检验斜率改变量和即刻水平改变量的显著性意义,从而评价干预效果[17]。如果在干预实施的时间窗口中存在多个政策转变,即潜在混杂因素可对结果变量产生影响,则需要谨慎使用单组ITS。多组ITS则可以较好处理这样的情况,主要是因为其核心假设是在干预实施之前实验组和对照组都受到了混杂因素的相同影响。此外,多组ITS的一个主要优势是能够评价两组之间因干预引起的差异的可比性,其中β4和β5两个参数用于确定实验组和对照组是否均衡起着特别重要的作用。如果这样的可比性无法很好地满足,可以通过基于倾向得分的加权模型对时间序列进行矫正后再采取ITS分析[18]。
使用ITS进行分析时应首先注意干预前后有清晰且明确的分界线。此外,干预引起的变化应在短期内即可观察到,或者需指定一个滞后时间。在数据方面,因等时间间隔收集40~50个观察点数据,或至少20个点在干预前,20个点在干预后。如果线性关系不能很好满足,则需考虑采取相应变换。如果只有几个观察点,则不适合用ITS分析,可改为重复测量方差分析、多重t检验、广义估计方程(generalized estimation equation,GEE)、Poisson回归或面板数据模型。除使用线性回归以外,ITS可使用广义线性模型,如计数资料使用泊松回归,分类资料使用logit回归。
单组ITS常存在一阶自相关的原因,可以考虑使用Prais-Winsten法进行参数估计,是因为普通线性回归使用OLS无法在存在自相关错误的情况下提供一致的区间估计。由于Prais-Winsten法和普通线性回归的原理截然不同,二者所得的结果不可能完全一致。如果两种方法提供相似的点估计结果,因其标准误差一致,首选Prais-Winsten法。而在多组ITS中,由于序列情况更加复杂,除典型一阶自相关以外,还存在潜在的高阶自相关以及异方差的情况(heteroscedasticity-and autocorrelation-consistent,HAC)[5]。在本研究中,使用Prais-Winsten法控制了一阶自相关的影响后,模型DW值为1.316,可见HAC对Prais-Winsten法影响较大,进而导致参数估计结果的改变;使用Prais-Winsten法对多组ITS数据进行参数估计时,即刻水平改变量β2=0.003,即表明在干预同时发病率增加了0.003,与事实不相符(图 2),即出现截然不同的结果。
本研究使用Newey-West法进行基于OLS的参数估计和标准误差的计算,可以在有效控制潜在高阶自相关和异方差等因素的同时,较好地实现参数估计[12]。Newey-West法在计算标准误差时需要考虑自相关阶数的最大值。经验上,年份相关数据考虑lag=1,季度数据考虑lag=4,月份数据考虑lag=12。本研究中使用newey控制了HAC后,模型残差满足正态性假设。此外,在拟合优度方面,Newey- West法的表现均好于Prais-Winsten法。在某些情况下,如果异方差存在波动性(dynamic form of heteroskedasticity),则需进一步考虑使用自回归条件异方差模型(autoregressive conditional heteroskedasticity,ARCH)[19]。
综上所述,本研究通过介绍了两组ITS原理以及应用实例,为项目评价提供了新的思路。两组ITS相比较单组ITS,不仅继承了ITS的类实验设计方法的优点,更能进一步控制干预前已存在的趋势,为干预的评价提供更准确的结论。此外,应用ITS时需注意时间序列潜在的高阶自相关,选择合适的方法进行处理,避免因此带来错误的参数估计结果。
利益冲突 所有作者均声明不存在利益冲突
| [1] |
Biglan A, Ary D, Wagenaar AC. The value of interrupted time-series experiments for community intervention research[J]. Prev Sci, 2000, 1(1): 31-49. DOI:10.1023/A:1010024016308 |
| [2] |
Hartmann DP, Gottman JM, Jones RR, et al. Interrupted time-series analysis and its application to behavioral data[J]. J Appl Behav Anal, 1980, 13(4): 543-559. DOI:10.1901/jaba.1980.13-543 |
| [3] |
Wagner AK, Soumerai SB, Zhang F, et al. Segmented regression analysis of interrupted time series studies in medication use research[J]. J Clin Pharm Ther, 2002, 27(4): 299-309. DOI:10.1046/j.1365-2710.2002.00430.x |
| [4] |
Shadish WR, Cook TD, Campbell DT. Experimental and quasi-experimental designs for generalized causal inference[M]. Boston: Houghton Mifflin, 2002.
|
| [5] |
Linden A. Conducting interrupted time-series analysis for single-and multiple-group comparisons[J]. Stata J, 2015, 15(2): 480-500. DOI:10.1177/1536867x1501500208 |
| [6] |
Linden A. A comprehensive set of postestimation measures to enrich interrupted time-series analysis[J]. Stata J, 2017, 17(1): 73-88. DOI:10.1177/1536867x1701700105 |
| [7] |
宁桂军, 吴丹, 李军宏, 等. 应用中断时间序列分析评价流行性乙型脑炎减毒活疫苗大规模预防接种的有效性[J]. 中国疫苗和免疫, 2015, 21(4): 361-364. Ning GJ, Wu D, Li JH, et al. Application of interrupted time series analysis on an assessment of effectiveness of a catch-up campaign with Japanese encephalitis attenuated live vaccine[J]. Chin J Vaccin Immun, 2015, 21(4): 361-364. |
| [8] |
李珍, 曲波, 胡美霞, 等. 处方点评制度对抗生素使用的影响——基于山东省青岛市村卫生室的时间序列分析[J]. 中国卫生政策研究, 2013, 6(10): 54-59. Li Z, Qu B, Hu MX, et al. The impact of a peer review and feedback intervention on antibiotic prescribing:interrupted time series analysis at village clinics in Qingdao, Shandong province[J]. Chin J Health Policy, 2013, 6(10): 54-59. DOI:10.3969/j.issn.1674-2982.2013.10.010 |
| [9] |
Senter HF. Applied linear statistical models[J]. J Ame Statist Associa, 2008, 103(482): 880. DOI:10.1198/016214508000000300 |
| [10] |
Prais SJ, Winsten CB. Trend estimators and serial correlation[R]. Cowles Commission discussion paper No. 383. Chicago: University of Chicago, 1954.
|
| [11] |
Wooldridge JM. Introductory econometrics:a modern approach[M]. 4th ed. Nelson Education, South-Western, 2015.
|
| [12] |
Newey WK, West KD. A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix[J]. Econometrica, 1987, 55(3): 703-708. DOI:10.2307/1913610 |
| [13] |
Newey WK, West KD. Automatic lag selection in covariance matrix estimation[J]. Rev Econ Stud, 1994, 61(4): 631-653. DOI:10.2307/2297912 |
| [14] |
Smith RJ. Automatic positive semidefinite HAC covariance matrix and GMM estimation[J]. Econom Theory, 2005, 21(1): 158-170. DOI:10.1017/s0266466605050103 |
| [15] |
Hulland E, Subaiya S, Pierre K, et al. Increase in reported cholera cases in Haiti following hurricane Matthew:an interrupted time series model[J]. Am J Trop Med Hyg, 2019, 100(2): 368-373. DOI:10.4269/ajtmh.17-0964 |
| [16] |
Morgan L, Hadi M, Pickering S, et al. The effect of teamwork training on team performance and clinical outcome in elective orthopaedic surgery:a controlled interrupted time series study[J]. BMJ Open, 2015, 5(4): e006216. DOI:10.1136/bmjopen-2014-006216 |
| [17] |
Ramsay CR, Matowe L, Grilli R, et al. Interrupted time series designs in health technology assessment:lessons from two systematic reviews of behavior change strategies[J]. Int J Technol Assess Health Care, 2003, 19(4): 613-623. DOI:10.1017/s0266462303000576 |
| [18] |
Linden A, Adams JL. Applying a propensity score-based weighting model to interrupted time series data:improving causal inference in programme evaluation[J]. J Eval Clin Pract, 2011, 17(6): 1231-1238. DOI:10.1111/j.1365-2753.2010.01504.x |
| [19] |
Bollerslev T. Generalized autoregressive conditional heteroscedasticity[J]. J Econom, 1986, 31(3): 307-327. DOI:10.1016/0304-4076(86)90063-1 |
 2019, Vol. 40
2019, Vol. 40