文章信息
- 言晨绮, 王瑞白, 刘海灿, 蒋毅, 李马超, 尹树鹏, 肖彤洋, 万康林, 让蔚清.
- Yan Chenqi, Wang Ruibai, Liu Haican, Jiang Yi, Li Machao, Yin Shupeng, Xiao Tongyang, Wan Kanglin, Rang Weiqing.
- ARIMA模型预测2018-2019年我国肺结核发病趋势的应用
- Application of ARIMA model in predicting the incidence of tuberculosis in China from 2018 to 2019
- 中华流行病学杂志, 2019, 40(6): 633-637
- Chinese journal of Epidemiology, 2019, 40(6): 633-637
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2019.06.006
-
文章历史
收稿日期: 2018-11-29
2. 中国疾病预防控制中心传染病预防控制所 传染病预防控制国家重点实验室 感染性疾病诊治协同创新中心, 北京 102206
2. State Key Laboratory for Infectious Diseases Prevention and Control, Collaborative Innovation Center for Diagnosis and Treatment of Infectious Diseases, National Institute for Communicable Disease Control and Prevention, Chinese Center for Disease Control and Prevention, Beijing 102206, China
结核病是由结核分枝杆菌引起的一种慢性感染性疾病,而肺结核占结核病总数的90%以上[1]。肺结核主要在发展中国家流行,中国位列全世界结核病高负担国家的前二至三位。近年来,随着WHO推广实施的督导短程化疗策略(Directly Observed Treatment+Short Course,DOTS)的全面覆盖和一系列结核防治规划的出台,我国新发肺结核患者数逐渐减少,但由于人口众多、地域差别、各地风俗习惯、经济发展水平等因素影响[2-3],我国肺结核疫情仍然严重,为响应WHO提出的2035年终止结核病行动,实现发病率较2015年减少90%这一目标,深度剖析现有结核病流行情况并依此建立预测模型,对结核病未来的发病情况进行早期预测[4]。
自回归移动平均(ARIMA)模型可以对有季节效应的序列进行建模,根据其季节性提取的难易程度又可分为简单季节模型和乘积季节模型,乘积季节模型能提取出序列的季节效应、长期趋势效应和随机波动效应的相互影响[5]。本研究利用2005-2017年我国肺结核疫情资料,基于R 3.4.4软件建立ARIMA乘积季节模型,选择最优模型对我国2018年和2019年结核病疫情进行预测,为有关部门制定结核病防治策略提供参考依据。
资料与方法1.资料来源:中国疾病预防控制信息系统传染病疫情信息网络直报系统2005年1月至2017年12月肺结核监测数据。其中2005年1月至2017年6月肺结核月发病数用于ARIMA模型拟合,2017年7-12月的数据用于ARIMA模型检验。
2.研究方法:ARIMA模型是20世纪70年代由Box和Jenkins提出的一种时间序列的预测方法[6],其基本思想是将一个随着时间推移而形成的数列视为一组随机序列,用数学模型对其进行描述,从而根据已发生的既往序列值来预测未来值[7]。ARIMA模型主要有AR(P)模型、MA(q)、ARMA(p,q)、ARIMA(p,d,q)和ARIMA(p,d,q)×(P,D,Q)s 5种形式,其中ARIMA(p,d,q)×(P,D,Q)s可以将时间序列中季节性因素与非季节部分相结合,模型中p和q分别为非季节自回归阶数和非季节移动平均阶数,d为非季节差分阶数,P和Q分别是季节自回归阶数和季节移动平均阶数,D是季节差分的阶数,s是季节长度,由于大多数传染病都具有复杂的季节效应,因此研究中常使用ARIMA乘积季节模型对传染病的流行趋势进行预测,ARIMA乘积模型表达式[7]:

其中:
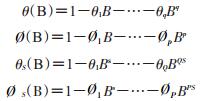
3.统计学分析:使用Excel 2016软件建立肺结核月发病数据库,利用R 3.4.4软件对数据进行建模、分析和预测。以P<0.05为差异有统计学意义。
(1)数据预处理:ARIMA模型建立的前提条件是要求时间序列具有平稳性,通过做出原始序列图对其进行直观判断,如果方差不是常数,则应该使用数据变换或者差分的方法使数据平稳,此外,可以通过ADF(Augmented Dickey-Fuller)检验来验证序列的平稳性,该检验的原假设数据不平稳(存在单位根),备择假设是数据平稳。
(2)模型的识别:对于预处理后达到平稳性要求的序列,绘制自相关图(autocorrelation function,ACF)和偏相关图(partial autocorrelation function,PACF),根据ACF图和PACF图截尾或拖尾的情况对p和q的阶值进行估计,若ACF图为拖尾,PACF图为截尾,则适用AR(p)模型,PACF截尾的值则为p值。反之,则选择MA(q)模型,ACF图截尾的值是q值。若ACF和PACF图均拖尾,则考虑ARIMA(p,d,q)模型。参数P和Q的值较难判断,一般采用从低阶到高阶逐步尝试的方法,取值通常不超过2。
(3)参数估计和模型诊断:在R软件中导入forecast包使用“fit()”函数运用最大似然估计法(maximum likelihood estimation,MLE)对模型参数进行估计,再对模型的残差序列进行白噪声检验,若统计量显示差异无统计学意义,则表示残差为白噪声,再通过对比备选模型的赤迟信息量准则(Akaike information criterion,AIC)和贝叶斯信息准则(Bayesian information criterion,BIC)值等系数,选择AIC值和BIC值最小的模型为最佳ARIMA模型。
(4)模型预测效果评估:用最优ARIMA模型对2005年1月至2017年12月的数据进行拟合,通过比对2017年7-12月的数据评价模型效果,若模型准确度较高则对2018和2019年我国肺结核月发病数进行进一步预测。
结果1.全国肺结核流行趋势:2005年1月至2017年12月,共有13 022 675例肺结核患者,从原始发病序列(图 1)可以看出,2005年发病人数最多,随后逐年下降,2017年较2015年发病数下降了33.68%。我国肺结核流行的季节性明显,每年冬春交替之际发病数最高。
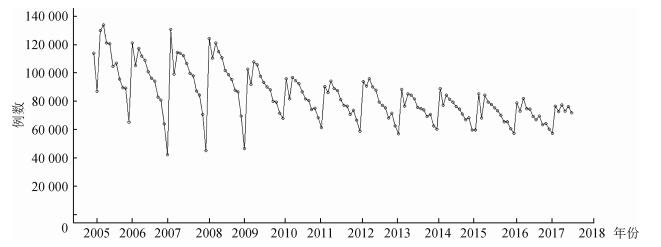
|
| 图 1 我国2005年1月至2017年6月肺结核发病数时间序列 |
2. ARIMA模型构建:
(1)数据的预处理:由原始序列图可看出数据存在明显的趋势性和季节性变化。使用“diff”语句对原始数据进行一阶12步季节差分,消除时间序列趋势和季节影响后,使用tseries包中的“adf.test”语句进行ADF检验,P=0.02,由此可知差分后数据满足平稳性要求。
(2)模型的识别:ARIMA模型中参数p和q的识别主要依据ACF图和PACF图截尾或拖尾的情况,对差分后序列做自相关分析图(图 2)和偏自相关分析图(图 3),自相关分析图显示在2阶后均落入置信区间,偏自相关函数图则显示拖尾,p=0。根据差分的次数和数据的周期情况初步判定模型为ARIMA(0,1,2)(P,1,Q)12,P和Q一般取值0~2,采取从低阶到高阶的顺序进行测试,根据模型的拟合优度指标进行比较与判断。

|
| 图 2 差分后的ACF函数 |
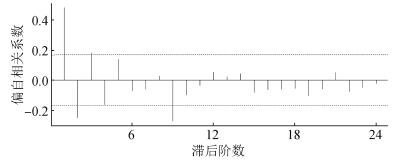
|
| 图 3 差分后的PACF函数 |
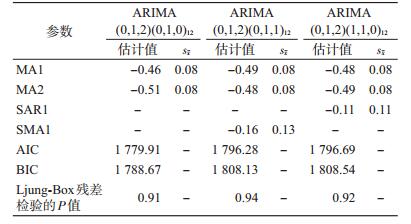
(3)参数估计和模型诊断:根据以上信息,对模型统计学检验的结果进行调试,选择了3个备选模型,其参数估计值和Ljung-Box残差检验(L-B检验)结果,见表 1。3个模型的残差均为白噪声(L-B检验,P>0.05),其中ARIMA(0,1,2)(0,1,0)12模型AIC值和BIC值最小,综合以上信息确定此模型为最优模型。模型表达为:∇∇12=(1+0.46B+0.51B2)εt。
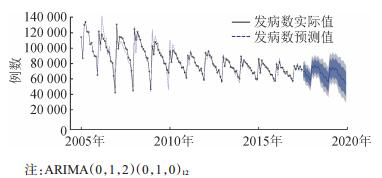
(4)模型预测效果评估:用“forecast”函数包对我国2005年1月至2017年12月肺结核发病情况进行拟合,用2017年7-12月的预测值与实际值相比较,表 2为2017年7-12月我国肺结核发病数预测结果,由表可知我国肺结核月发病数都落在预测值(95%CI)范围内,提示该模型预测性能较好。将模型拟合的2005年1月至2019年12月预测发病数与真实值比较发现(图 4),模型预测的趋势与实际趋势一致,2018和2019年我国肺结核患者数会略有下降。
|
| 图 4 2005-2019年我国肺结核发病数预测 |
目前用于公共卫生领域的统计预测分析的主要有回归分析和时间序列分析2种方法,其中,一般的线性回归模型需要对各种影响因素进行分析,而时间序列分析主要是以时间为变量,利用事物发展的延续性建立数据模型,其中,ARIMA乘积季节模型能较好地将时间序列的依存性与随机干扰因素相结合,已经能成熟地运用在疾病的预测领域[8-11]。
本研究利用2005年1月至2017年6月我国肺结核月发病数据拟合了ARIMA乘积季节模型。因为我国传染病收录系统在2004年由以县为单位的月报转变为基于医院的电子实时报告[12],因此选择2005年后的发病数据可以规避统计口径不一致、报告数据质量不同所造成的影响[13]。基于这段数据,我们拟合出了ARIMA(0,1,2)(0,1,0)12模型,通过模型预测,我国2018年新增肺结核患者约为789 509人,2019年新增患者数为760 165人。本研究结果显示我国肺结核流行主要有以下特征:第一,季节性明显。发病主要集中在冬末春初时节,其中每年2月报告病例呈现明显低谷,主要原因是我国春节基本上在2月份,由于风俗习惯的影响,这段时间就医人数会减少,3月份患者数则会达到峰值,形成“春节效应”[14-15]。此后由于季节影响,新发患者数逐渐减少,从图 4可以看到,该模型能准确拟合出我国肺结核流行的这一特征。第二,我国肺结核发病数总体呈现下降趋势。2017年报告患者数较2005年减少了424 116人,12年间平均每年降幅为2.81%,由此可见,随着DOTS策略的全面覆盖及我国结核病防治规划的落实,我国结核病的流行得到了一定程度上的控制。第三,2015年后我国结核病下降速度减缓。按终止结核策略(2016-2035年),2035年结核病发病率应较2015年下降90%(发病率下降至6.34/10万),此外,终止结核病行动还设定了第1个里程碑目标,即2020年发病率较2015年降低20%,届时,发病率应降低到50.2/10万,2015-2020年每年发病率应减少4%~5%。通过本次研究,我国结核病发病率虽然处于下降阶段,但下降速度并不理想,2016-2017年仅下降0.58%,这与实现终止结核病策略的目标还存在相当的差距,而我国控制结核病进程中仍存在诸多障碍:不同地区结核病流行情况不平衡,西部地区较贫困,少数民族较多,医疗卫生服务条件较差,结核病防治人力资源匮乏,因此该地区肺结核疫情严重[16];此外,我国结核病患者的中老年人比例较高,他们收入不高,免疫系统功能开始衰退,是结核病的主要易感人群[3, 17-18],而我国老龄化日益严重。因此,要达到WHO的消灭结核病任务仍有很多挑战。
综上,ARIMA(0,1,2)(0,1,0)12模型对我国肺结核发病数的拟合效果较好,可用于我国肺结核的短期预测和动态分析,具有较好的应用价值。
利益冲突 所有作者均声明不存在利益冲突
| [1] |
全国第五次结核病流行病学抽样调查技术指导组, 全国第五次结核病流行病学抽样调查办公室. 2010年全国第五次结核病流行病学抽样调查报告[J]. 中国防痨杂志, 2012, 34(8): 485-508. Technical Guidance Group for the Fifth National Tuberculosis Epidemiological Sampling Survey, Office of the Fifth National Sample Survey of Tuberculosis Epidemiology. The fifth national tuberculosis epidemiological survey in 2010[J]. Chin J Antituberc, 2012, 34(8): 485-508. |
| [2] |
成诗明.结核病疫情监测与分析: 2016年结核病防治服务体系建设研讨会资料汇编[C].西安: 中国防痨协会, 2016. Cheng SM. TB surveillance and analysis: 2016 seminar on TB control service system construction[C]. Xi'an: Chinese Antituberculosis Association, 2016. |
| [3] |
王巧智, 龚德华. 结核病疫情现状和控制策略[J]. 实用预防医学, 2017, 24(3): 257-259, 351. Wang QZ, Gong DH. Epidemic and control strategy of tuberculosis[J]. Pract Prev Med, 2017, 24(3): 257-259, 351. DOI:10.3969/j.issn.1006-3110.2017.03.001 |
| [4] |
Shargie EB, Lindtjørn B. DOTS improves treatment outcomes and service coverage for tuberculosis in South Ethiopia:a retrospective trend analysis[J]. BMC Public Health, 2005, 5(1): 62. DOI:10.1186/1471-2458-5-62 |
| [5] |
Li Q, Guo NN, Han ZY, et al. Application of an autoregressive integrated moving average model for predicting the incidence of hemorrhagic fever with renal syndrome[J]. Am J Trop Med Hyg, 2012, 87(2): 364-370. DOI:10.4269/ajtmh.2012.11-0472 |
| [6] |
方积乾, 陆盈. 现代医学统计学[M]. 北京: 人民卫生出版社, 2002. Fang JQ, Lu Y. Advanced Medical Statistics[M]. Beijing: People's Medical Publishing House, 2002. |
| [7] |
王燕. 应用时间序列分析[M]. 北京: 中国人民大学出版社, 2005. Wang Y. Application of Time Series Analysis[M]. Beijing: Renmin University of China Press, 2005. |
| [8] |
王晨, 郭倩, 周罗晶. 基于R语言的ARIMA模型对流感样病例发病趋势的预测[J]. 中华疾病控制杂志, 2018, 22(9): 957-960. Wang C, Guo Q, Zhou LJ. Forecast of incidence trend of influenza-like illness by the ARIMA model based on R[J]. Chin J Dis Control Prev, 2018, 22(9): 957-960. DOI:10.16462/j.cnki.zhjbkz.2018.09.020 |
| [9] |
易燕飞.基于时间序列模型的传染病流行趋势及预测研究[D].长春: 长春工业大学, 2016. Yi YF. Epidemic prediction of infectious diseases based on time series model[D]. Changchun: Changchun University of Technology, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10190-1016759377.htm |
| [10] |
张蔚, 张彦琦, 杨旭. 时间序列资料ARIMA季节乘积模型及其应用[J]. 第三军医大学学报, 2002, 24(8): 955-957. Zhang W, Zhang YQ, Yang X. Model of multiple seasonal ARIMA and its application to data in time series[J]. J Third Military Med Univ, 2002, 24(8): 955-957. DOI:10.3321/j.issn:1000-5404.2002.08.026 |
| [11] |
Lin Y, Chen M, Chen GW, et al. Application of an autoregressive integrated moving average model for predicting injury mortality in Xiamen, China[J]. BMJ Open, 2015, 5(12): e8491. DOI:10.1136/bmjopen-2015-008491 |
| [12] |
Wang LD, Wang Y, Jin SG, et al. Emergence and control of infectious disease in China[J]. Lancet, 2008, 372(9649): 1598-1605. DOI:10.1016/S0140-6736(08)61365-3 |
| [13] |
Luz PM, Mendes BVM, Codeço CT, et al. Time series analysis of dengue incidence in Rio de Janeiro, Brazil[J]. Am J Trop Med Hyg, 2008, 79(6): 933-939. DOI:10.4269/ajtmh.2008.79.933 |
| [14] |
吕锐利. 春节效应对传染病网络直报工作的影响[J]. 中国热带医学, 2014, 14(11): 1364-1366. Lyu RL. The impact of the Spring festival effect on the direct network reporting of communicable diseases[J]. Chin Trop Med, 2014, 14(11): 1364-1366. DOI:10.13604/j.cnki.46-1064/r.2014.11.022 |
| [15] |
魏珊, 陆一涵, 高眉扬, 等. 中国主要法定报告传染病的"春节效应"研究[J]. 复旦学报:医学版, 2013, 40(2): 153-158. Wei S, Lu YH, Gao MY, et al. "Spring Festival effects" on the main notifiable communicable diseases in China[J]. Fudan Univ J Med Sci, 2013, 40(2): 153-158. DOI:10.3969/j.issn.1672-8467.2013.02.005 |
| [16] |
李新旭, 周晓农, 王黎霞. 结核病空间分布特征及影响因素研究进展[J]. 中国公共卫生, 2014, 30(1): 102-106. Li XX, Zhou XN, Wang LX. Advances in studies on spatial distribution characteristics and influencing factors of tuberculosis[J]. Chin J Public Health, 2014, 30(1): 102-106. DOI:10.11847/zgggws2014-30-01-31 |
| [17] |
Wu B, Yu Y, Xie WJ, et al. Epidemiology of tuberculosis in Chongqing, China:a secular trend from 1992 to 2015[J]. Scientific Reports, 2017, 7(1): 7832-7837. DOI:10.1038/s41598-017-07959-2 |
| [18] |
沈鑫, 潘启超, 肖和平. 结核病研究新进展[J]. 上海预防医学, 2016, 28(3): 143-146, 173. Shen X, Pan QC, Xiao HP. New progress in tuberculosis research[J]. Shanghai J Prev Med, 2016, 28(3): 143-146, 173. DOI:10.19428/j.cnki.sjpm.2016.03.004 |
 2019, Vol. 40
2019, Vol. 40