文章信息
- 何一宁, 刘丽丽, 蔡倩莹, 赵耐青, 郑英杰.
- He Yining, Liu Lili, Cai Qianying, Zhao Naiqing, Zheng Yingjie.
- 研究设计时混杂控制策略的结构分类
- A structural classification of strategies for confounding control in research design
- 中华流行病学杂志, 2018, 39(7): 999-1002
- Chinese Journal of Epidemiology, 2018, 39(7): 999-1002
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2018.07.025
-
文章历史
收稿日期: 2017-11-23
2. 200032 上海, 复旦大学公共卫生学院流行病学教研室;
3. 200032 上海, 复旦大学公共卫生学院生物统计学教研室;
4. 200032 上海, 复旦大学公共卫生学院公共卫生安全教育部重点实验室;
5. 200032 上海, 复旦大学公共卫生学院国家卫生和计划生育委员会卫生技术评估重点实验室
2. Department of Epidemiology, School of Public Health, Fudan University, Shanghai 200032, China;
3. Department of Biostatistics, School of Public Health, Fudan University, Shanghai 200032, China;
4. Key Laboratory of Public Health Safety, Ministry of Education, School of Public Health, Fudan University, Shanghai 200032, China;
5. Key Laboratory for Health Technology Assessment, National Commission of Health and Family Planning, School of Public Health, Fudan University, Shanghai 200032, China
因果关系研究通常围绕着一个特定暴露(X,如吸烟)与一个拟研究结局(Y,如肺癌)进行。外来干扰因素影响X-Y因果关联的估计存在着8种基本的因果结构[1],其中仅有混杂结构影响着X-Y总效应的估计。在人类识别这种效应前,混杂结构在易感人群中静默地发生着[2],使得拟研究结局表现出特有的人群分布特征。
正确的因果效应估计是所有因果关系研究的目标,控制所有的混杂成为实现这一目标的基本前提。通常做法是,在设计上采用合适的策略,如限制或匹配,尽可能收集已知的可测量的混杂因素,予以准确测量,并采用回归模型等数据分析方法,以达到控制混杂的目的。
目前大多数研究都期望能在获得X-Y统计学关联之后,通过排除法(真或假关联)或通行的病因标准而能达到因果关联的推断结论,但在实际操作中往往极难实现[3]。有向无环图(Directed Acyclic Graphs,DAGs)是因果关系研究的图形工具[1, 4-6],对研究涉及的暴露、结局及其干扰等因素,必须进行各变量之间是否存在因果效应的判断;虽然这个工作看似困难,但研究实施前的充分思考,不但能为形成正确的因果关系整体框架奠定基础,从而达到有效指导研究问题的提出、设计选择和数据分析的目的,而且可为分析结果的因果推断奠定基础[3]。本文尝试采用DAGs对研究设计时如何控制混杂的策略进行分类,并探索这种分类的意义。
1.混杂的因果结构及分类:
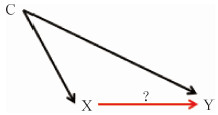
假定X为我们拟研究的暴露变量(如慢性乙型肝炎病毒感染),Y为拟研究的结局变量(如原发性肝细胞癌),C为干扰X-Y效应估计的混杂变量(如性别、年龄等)。绘制出混杂的因果结构(图 1),其中C→X和C→Y同时成立(C为X和Y的共同病因,也称共病因结构),形成了混杂路径X←C→Y,混杂了X-Y的效应。因病因是关联的基础,据此结构可很容易推出判断混杂的统计学标准;虽然,反过来的结论并不成立[3]。
|
| 图 1 混杂的因果结构 |
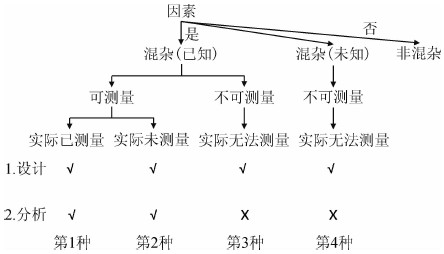
影响X-Y效应估计的因素众多,依据混杂的共病因结构(图 1),可将其区分为混杂因素和非混杂因素。前者又可根据是否已知、可测量及具体是否测量等情况,将混杂分为4种情形(图 2)。
|
| 图 2 混杂的分类 |
(1)科学家已认识、可测量并已测量的混杂:当前研究多数为这种情形。因混杂已知、可测量,在研究的设计和分析阶段中,均可采用常规的混杂控制策略予以解决。
(2)科学家已认识、可测量但未测量的混杂:虽然混杂已知、可测量,但在实际工作中因各种原因未予以测量,如回顾性队列研究中重要混杂未记录、设计考虑不够周密,或随着科学发展出现新的认识等。针对这类混杂,通常可采用定量偏倚分析,作为补救措施予以解决[7]。
(3)科学家已认识、但实际无法测量的混杂:虽然混杂已知,但对其测量不可行或难以测量,如社会经济状况,虽然通常被认为是暴露-结局关系研究的重要混杂。
(4)科学家未知的混杂:如小量饮酒可能降低冠心病的风险,虽然怀疑其中存在着混杂,但具体是什么因素起着混杂干扰作用仍不清楚[8]。这类混杂的存在,将给暴露-结局的效应估计造成困难。
获得正确的X-Y因果关联估计是研究的目标,在研究设计阶段,充分考虑混杂对X-Y的干扰是尤为关键的一步,并指导着后续研究的具体实施、变量的测量和结果的分析。因此,如何控制上述4类混杂成为需要解决的问题。
2.混杂结构的控制策略:
那么该如何进行混杂的控制呢?从混杂的因果结构及其构成路径来看(图 1),如有合适的策略或措施,如打断混杂路径使得混杂结构的完整性被破坏,则混杂自然得以控制,这构成了本文建立混杂控制策略的基本思路。
(1)第一种策略:混杂路径打断法。依据DAGs的规则,打断混杂路径上的任一因果关系,这样混杂路径自然消失,即可起到控制混杂的作用。具体可分为:①打断C→X(图 3A):相当于暴露干预完全法。通过设置合适的外部变量(Z)进行干预,即相当于在混杂结构的基础上建立人为的因果路径Z→X。若暴露X完全由Z所决定,此时C→X自然不成立,从而起到打断混杂路径的目的。这类设计即随机对照试验(Randomized Control Trials,RCTs),当随机化方法(Z)完全决定了研究对象的X取值(图 3A),即Z=X。该策略适用于上述混杂的所有4种情形,即已知和未知的、可测量和不可测量、已测量和未测量的混杂均可有效控制。理论上说此时X-Y效应估计不受混杂因素测量与否的影响,这也是在进行因果关系研究时RCTs优于其他设计的结构基础。②打断C→Y(图 3B):同样通过设置外部干预变量Z,即相当于在混杂结构的基础上建立人为的因果路径Z→Y;此时对Y的决定因素包括了混杂C、干预变量Z和拟估计的暴露X。理论上来说,如能恰好获得合适的变量Z,可使得C→Y的效应恰好为Z→Y的效应所抵消,则混杂得以控制。然而实际上的操作相当困难。③同时打断C→X和C→Y(图 3C):第一种:限制法,如性别为混杂,则研究对象只招募男性或女性;第二种:分层法,如性别为混杂,则通过分层法分别在男性或女性人群中研究X-Y的关系。此时C取值只有一个固定值,因此双路径(C→X和C→Y)同时不成立(被打断)。在分析阶段时,通过分层分析、多因素分析等手段来调整C,可同样达到混杂控制的效果,这也是数据分析阶段唯一可以实现的控制手段。这种策略适用于上述混杂的第一种情形,即混杂已知、可测量并且在实际研究实施中已进行了测量。这也是现有因果关系研究中混杂控制最为常用的策略之一。

|
| 注:图中蓝色双短线代表着该路径两个变量之间的因果关系被打断 图 3 混杂控制策略-混杂路径打断法 |
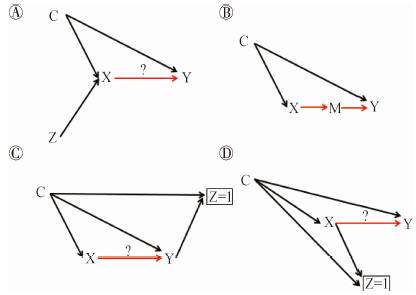
(2)第二种策略:混杂路径保留法:如果混杂结构中任意一条路径均无法被打断,则一般可通过以下几种办法进行混杂控制。①暴露不完全干预法(图 4A):延续2(1)①的策略,仍然通过设置合适的外部变量(Z)干预,此时暴露X可部分由Z决定,此时C→X路径不能被打断而仍然成立,如工具变量设计(Instrumental variabledesign,IV)[9-10]或孟德尔随机化设计(Mendelian randomization design)[11-13]。因Z为外源变量(不受混杂路径影响),通过估计无混杂的Z→X和Z→Y,从而间接估计X-Y的效应。这种策略同样地适用于上述混杂的4种情形。②中间变量法(图 4B):通过寻找X→Y之间合适的中间变量(M),此时可通过估计无混杂的X→M和调整X而获得无混杂的M→Y(因X为研究因素,是必须测量的),从而间接估计X-Y的效应。这种策略亦同样地适用于上述混杂的4种情形。Lange等[14]曾发表相关综述,文中对中间变量法做了详细的介绍及导读。③匹配法(图 4C和图 4D):匹配常常用于病例对照研究和队列研究设计,用于控制重要的或通常难以测量的混杂,其匹配混杂的DAGs分别对应于图 4C和4D。匹配依据混杂因素决定研究对象是否纳入研究(Z),因此图 4C和图 4D中C→Z成立。同时为了实现匹配使得组间变量的均衡性,病例对照研究对病例组和对照组之间的混杂因素实施匹配,故Y→Z成立;而队列研究对暴露组和非暴露组之间的混杂因素实施匹配,故C→Y成立(图 4D)。因匹配研究在分析时,只对纳入研究(Z=1)的暴露组和非暴露组(队列研究)或病例组和对照组(病例对照研究)进行,因此相当于对Z进行调整并且只可获得Z=1层的分析结果。这种策略适用于上述混杂的第一种和第三种情形。
|
| 图 4 混杂控制策略-混杂路径保留法 |
从混杂路径保留法上来看,3种方法的混杂结构/路径未被破坏而仍保留,但其控制混杂的机制不同:暴露不完全干预法和中间变量法实际上相当于忽视了混杂路径的存在,并且只能间接估计X-Y之间的效应。在混杂结构的完整性被保留并仍需进行正确因果效应的估计时,这两种方法在选择干预变量或中间变量时,通常不太容易。而匹配法虽可直接估计X-Y之间的效应,但其机制在于经由C→X所产生的混杂效应被因匹配而有意引入的选择性偏倚(因调整Z,关闭路径C→Z←X(图 4C)/C→Z←Y(图 4D)转为开放,而导致C-X/C-Y出现新的关联)所抵消[15-16]:在队列研究或X-Y为零效应的病例对照研究时,这种抵消是完全的,即混杂效应等于上述新引入的选择性偏倚;而在X-Y为非零效应的病例对照研究中,这种抵消不完全,受到路径C→X→Y的影响。这也解释了在数据分析时,匹配设计的队列研究通常不需要再调整匹配因素,而匹配设计的病例对照研究则通常需要。
混杂是干扰因果效应研究的固有现象,是研究设计需首先考虑的,并可结合数据分析阶段的控制策略,以达到混杂的完全控制为目标,构成了获得正确因果效应估计的基础。虽然混杂的因果结构仅有一个,但具体的控制策略却有多种,取决于混杂类型、研究设计、可行性等诸多因素。
本文应用DAGs,从研究设计阶段对混杂的控制策略进行分析与归类,揭示了控制混杂策略的结构基础。在研究设计时,应结合DAGs正确判断与X-Y效应估计的可能因素是否为混杂因素,列出所有的混杂因素,应努力寻找合适的工具变量、中间变量或干预变量,尽可能使用可控制4种情形的混杂的设计方法。当无法完全控制上述4种情形的混杂时,X-Y效应的估计将不可避免地出现残留混杂,尤其是观察性设计,在解释时应较为谨慎。
本文主要提出在研究设计时对混杂的控制策略,现实的研究将涉及具体的人群招募及抽样、测量、分析策略、可行性等,任何可能影响文中提及的因果结构的关系,将可能对混杂控制的策略及因果效应的估计产生影响。
利益冲突: 无
| [1] |
郑英杰, 赵耐青. 有向无环图:语言、规则及应用[J]. 中华流行病学杂志, 2017, 38(8): 1140–1144.
Zheng YJ, Zhao NQ. Directed acyclic graphs:languages, rules and applications[J]. Chin J Epidemiol, 2017, 38(8): 1140–1144. DOI:10.3760/cma.j.issn.0254-6450.2017.08.029 |
| [2] |
郑英杰, 赵耐青, 何一宁. 客观世界的因果关系:基于有向无环图的结构解析[J]. 中华流行病学杂志, 2018, 39(1): 96–99.
Zheng YJ, Zhao NQ, He YN. Causality in objective world:Directed Acyclic Graphs-based structural parsing[J]. Chin J Epidemiol, 2018, 39(1): 96–99. DOI:10.3760/cma.j.issn.0254-6450.2018.01.019 |
| [3] | Rothman KJ, Greenland S, Lash TL.Modern Epidemiology[M]. 3rd ed. Philadelphia: Lippincott Williams & Wilkins, 2008: 5–31. |
| [4] | Pearl J.Causality:Models, Reasoning and Inference[M]. Cambridge: Cambridge University Press, 2009: 1–102. |
| [5] | Greenland S, Brumback B. An overview of relations among causal modelling methods[J]. Int J Epidemiol, 2002, 31(5): 1030–1037. DOI:10.1093/ije/31.5.1030 |
| [6] | Pearl J. An introduction to causal inference[J]. Int J Biostat, 2010, 6(2): 7. DOI:10.2202/1557-4679.1203 |
| [7] | Lash TL, Fox MP, Fink AK.Applying Quantitative Bias Analysis to Epidemiologic Data[M]. New York: Springer, 2009: 13–32. |
| [8] | Poikolainen K, Vahtera J, Virtanen M, et al. Alcohol and coronary heart disease risk-is there an unknown confounder?[J]. Addiction, 2005, 100(8): 1150–1157. DOI:10.1111/j.1360-0443.2005.001126.x |
| [9] | Rothman K, Greenland S, Lash T.Modern Epidemiology[M]. 3rd ed. Philadelphia: Wolters Kluwer Lippincott Williams & Wilkins, 2008: 32–50. |
| [10] | Brookhart MA, Wang PS, Solomon DH, et al. Evaluating short-term drug effects using a physician-specific prescribing preference as an instrumental variable[J]. Epidemiology, 2006, 17(3): 268–275. DOI:10.1097/01.ede.0000193606.58671.c5 |
| [11] | Sekula P, Del Greco MF, Pattaro C, et al. Mendelian randomization as an approach to assess causality using observational data[J]. J Am Soci Nephrol, 2016, 27(11): 3253–3265. DOI:10.1681/Asn.2016010098 |
| [12] | Dale CE, Fatemifar G, Palmer TM, et al. Causal associations of adiposity and body fat distribution with coronary heart disease, stroke subtypes, and type 2 diabetes mellitus:a mendelian randomization analysis[J]. Circulation, 2017, 135(24): 2373–2388. DOI:10.1161/CIRCULATIONAHA.116.026560 |
| [13] |
秦雪英, 陈大方, 胡永华. 孟德尔随机化方法在流行病学病因推断中的应用[J]. 中华流行病学杂志, 2006, 27(7): 630–633.
Qin XY, Chen DF, Hu YH. Application of Mendelian randomization in the etiological study[J]. Chin J Epidemiol, 2006, 27(7): 630–633. DOI:10.3760/j.issn:0254-6450.2006.07.020 |
| [14] | Lange T, Hansen KW, Sørensen R, et al. Applied mediation analyses:a review and tutorial[J]. Epidemiol Health, 2017, 39: e2017035. DOI:10.4178/epih.e2017035 |
| [15] | Mansournia MA, Jewell NP, Greenland S. Case-control matching:effects, misconceptions, and recommendations[J]. Eur J Epidemiol, 2018, 33(1): 5–14. DOI:10.1007/s10654-017-0325-0 |
| [16] | Mansournia MA, Hernán MA, Greenland S. Matched designs and causal diagrams[J]. Int J Epidemiol, 2013, 42(3): 860–869. DOI:10.1093/ije/dyt083 |
 2018, Vol. 39
2018, Vol. 39


