文章信息
- 沈忠周, 马帅, 曲翌敏, 江宇.
- Shen Zhongzhou, Ma Shuai, Qu Yimin, Jiang Yu.
- ARIMA模型在我国法定传染病报告数中的应用
- Application of autoregressive integrated moving average model in predicting the reported notifiable communicable diseases in China
- 中华流行病学杂志, 2017, 38(12): 1708-1712
- Chinese journal of Epidemiology, 2017, 38(12): 1708-1712
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2017.12.025
-
文章历史
收稿日期: 2017-05-02
在人类活动加速全球化的今天传染病的发生和传播模式也在发生重大变化。近年来非常重要的旅游者传播:美国的一项研究显示,有6.3%的旅游者在传染病暴露期内发生疾病[1],且环境和气候的变化对传染病传播和发生也有很大的影响[2],同时传染病的频繁发生也使得人们对传染病产生了恐慌的心理。疫情监测是应对传染病的有效措施之一,同时疫情监测也是传染病防控的基础。在完善疫情监测系统的同时运用一定的数理统计方法,根据既往疾病的发病数据对未来发病情况进行预测预警研究也具有非常重要的意义,因此对传染病预测预警的研究逐渐成为疾病监测领域研究的重点[3]。我国对传染病预测预警的研究起步较晚,20世纪80年代有关传染病预测预警的理论和方法才开始应用,并逐渐成为疾病监测工作的热点。近年来有关自回归移动平均乘积季节(ARIMA)模型在疾病监测方面应用的文献报道越来越多,尤其是在传染病领域的应用,但大多是针对某地区某具体传染病开展的研究,而对于覆盖全部法定传染病的研究则相对较少,本团队查到的文献有冯丹等[4]于2007年开展的研究以及王怡等[5]2015年开展的研究。前者由于文献年限时间较长且我国法定传染病的病种也在不断地发生变化,所以该结果对现阶段的预测可能不太适用。后者建模的时间为2011年1月至2014年5月的报告数据,由于选取的时间较短,可能会产生偏倚。本研究选取2009年5月至2017年1月的法定传染病月报告发病数据进行研究,因为该统计数据较新且数据更多,因此建模会更稳定;另一方面此期间我国法定传染病报告病种变化不大,因而保证了总体相对稳定。本研究利用ARIMA模型拟合我国法定传染病的发生情况,以期为我国法定传染病的监测与防控提供科学的参考依据。
资料与方法1.数据来源:法定传染病月报告发病数数据(2009年5月至2017年1月)均来自于中国CDC网站[6](http://www.nhfpc.gov.cn/jkj/s3578/newlist.shtml)。其中2009年5月至2016年7月数据用于模型拟合,2016年8月至2017年1月的数据用于模型检验。
2.研究方法:目前最成熟的时间序列分析方法之一是ARIMA模型[7]。ARIMA模型最早是由美国学者Box和英国学者Jenkins提出的一整套关于经济学领域时间序列数据的分析和预测的方法[8],除了其本身之外还有AR(自回归模型)、MA(移动平均模型)和ARMA(自回归移动平均模型)3种类型。该模型的基本原理是根据给出的时间序列拟合出恰当的模型从而对未来的发生情况进行短期的预测,虽然ARIMA模型也可以对长期的情况进行预测,但其对短期的预测精度更高,在ARIMA(p,d,q)(P,D,Q)s模型中,(p,d,q)表示自回归移动平均拟合的过程,(P,D,Q)s表示季节拟合过程[9-10]。其中,p为非季节自回归阶数;d为趋势差分阶数;q为非季节移动平均阶数;P为季节自回归阶数;D为周期差分阶数;Q为季节移动平均阶数;s为季节长度[11]。
|
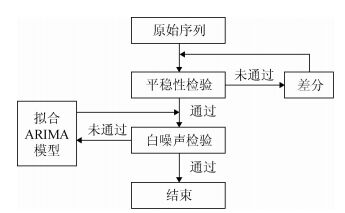
| 图 1 建模流程图 |
(1)预处理:包括平稳性和纯随机性检验。平稳性检验可通过时序图、自相关系数图(ACF)和偏自相关系数图(PACF)以及ADF检验得出。纯随机性可通过白噪声检验得出,是检验序列是否为纯随机数序列;如果序列是没有蕴含任何信息的纯随机序列则称序列为白噪声序列,对白噪声序列进行的纯随机性检验也叫白噪声检验。对原始序列预处理后只有结果显示为平稳非白噪声的序列才能进行下一步的分析;而非平稳的序列则须经过差分取对数等形式转变为平稳序列后进行分析,若原始序列经过预处理后显示为白噪声序列则停止分析。
(2)绘制ACF和PACF图:经预处理后用软件绘出ACF和PACF图判断相应的阶数值。
(3)模型拟合:根据ACF和PACF图的图形选择适当的阶数拟合ARIMA(p,d,q)(P,D,Q)s模型,也可根据R软件自带的“auto.arima()”功能拟合模型,本文使用这两种方法进行拟合。
(4)模型检验:检验拟合的模型是否理想。如果一个模型拟合有效则该模型的残差序列为白噪声序列,反之则认为模型拟合不够理想应重新拟合。
(5)模型优化:在模型检验中可能有多个备选模型通过白噪声检验,这时就要确定相对最优模型。为解决这一问题需要引入了AIC和SBC(BIC)信息准则进行模型优化:使两者达到最小值(通常识别AIC)的模型就认为是相对最优模型。之所以称相对最优模型而不是绝对最优模型是因为一般情况下很难对所有的模型进行拟合后比较他们的AIC和SBC值,因此通常只考察有限多个最可能的模型比较他们的AIC值。
(6)模型预测:用模型优化中确定的模型对未来几个月的发病情况进行短期的预测。
4.统计学分析:使用Excel 2007软件建立数据库,使用R 3.1.3软件进行建模和预测。
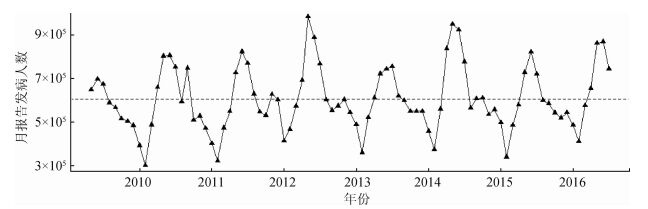
结果1.基本情况:2009年5月至2017年1月每月平均报告人数为606 344例,从时序图(图 2)可以看出每月报告发病病例数基本在平均线上下波动,提示这期间内社会经济因素变化较小满足时间序列应用的基本条件。另外,还提示法定传染病的发生每年都具有周期性并于2月报告人数达到最低,6月报告人数达到最高。
|
| 图 2 原始数据的时间序列图 |
2.构建ARIMA模型:
(1)预处理:通过对原始序列的预处理(diff=0,sdiff=0)和ADF检验(P<0.05)发现序列是平稳的,但是如果序列的时序图显示该序列有明显的趋势性或周期性那么他通常不是平稳序列[9-10]。根据时序图可以看出本序列具有很强的周期性,鉴于此对序列进行不同的差分处理[12]。
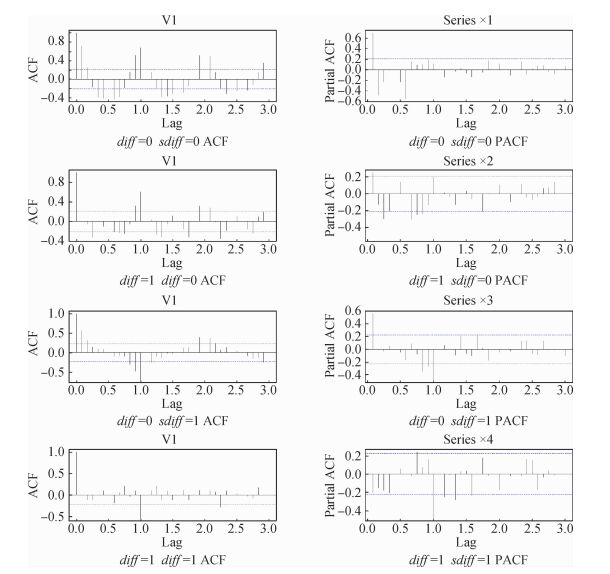
(2)绘制ACF和PACF图:分别对序列进行了(diff=1,sdiff=0)、(diff=0,sdiff=1)、(diff=1,sdiff=1)3种不同的差分方式,差分后的自相关图和偏自相关图见图 3。图 3表明经过(diff=1,sdiff=1)的差分后季节性得以消除效果最为理想,所以d=1,D=1。
|
| 图 3 原始序列差分图 |
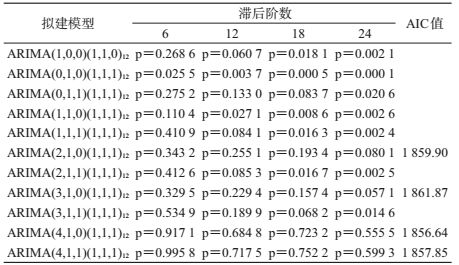
(3)模型拟合:使用“auto.arima()”函数得出的模型是ARIMA(1,0,0)(1,1,0)12;根据(diff=1,sdiff=1)的ACF和PACF图可以看出两者在12阶显著不为零而在24、36阶处都落在2倍标准差内,所以可以认为季节ACF和PACF截尾,因此P=Q=1。由于在一个季节周期(12阶)内ACF和PACF图均显示0阶截尾所以p、q可以取0,同时ACF在第1、7、9阶和PACF在第1、2、3、4、7、9阶较接近2倍的标准差。王燕[9-10]提到p和q取值一般不大于5,所以为了稳妥起见将p取值为(0,1,2,3,4),q取值为(0,1),共有10种组合方法。由“auto.arima()”函数和经验判断一共可以拟合出11种备选模型(表 1)。
(4)模型检验:经残差白噪声检验有4个模型残差检验符合白噪声的要求(表 1)。
(5)模型优化:根据AIC最小化原则选定ARIMA(4,1,0)(1,1,1)12为相对最优模型。
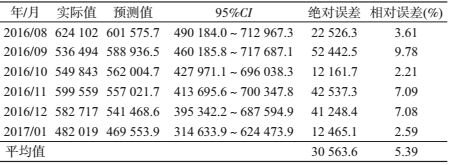
3.模型预测:确定最优模型后对建模序列之外的6个月(2016年8月至2017年1月)进行预测(表 2),预测值都落在95%的可信区间范围内,表明预测结果良好且预测的相对误差最大为9.78%,平均相对误差为5.39%。
本研究中对数据进行“混合”分析可能是最受关注的部分,在究竟能不能对这么多疾病进行“混合”建模的问题上,笔者通过查阅大量文献资料发现,对“混合”数据建立ARIMA模型的文章并不罕见。Lin等[13]最近使用ARIMA模型预测伤害的死亡数、Song等[12]使用中国2004-2011年流感发病数建立ARIMA模型、Cesar [14]使用ARIMA模型在疾病管理中的应用、黄建始等[15]在其主译的《循证公共卫生》中也提到过“混合”(synthetic)数据进行评估是很有效的一种方法,这种评估可以利用较大人群或地区内得到的结果估计较小人群或地区的某种情况。因此,认为使用ARIMA模型对“混合”后的法定传染病报告数进行建模和预测也是可行的。另外从ARIMA模型应用的本身也可以解释数据混合的可行性:该模型应用的基本条件是要求研究对象在一定的社会历史条件下保持相对稳定的状态,因为稳定状态是进行预测的前提。现阶段国内研究的热点多是集中在对具体传染病利用ARIMA模型[7, 12, 16-19],但国外已经有学者利用此模型对“混合”病种进行研究。如从对单一流感传染病[16](如H5N1流感)到流感传染病[12]再到对传染病甚至整个疾病范畴[14]的研究。本研究据此将国内法定传染病“混合”进行研究,因为越来越多的研究证实疾病之间以及疾病病因之间是错综复杂的,所以多病种联合分析以把握传染病的总体趋势或许是一种值得尝试的方法。
在使用软件建立ARIMA模型时大多数的软件都具有自动拟合模型的功能,如R软件的“auto.arima()”功能。本研究使用R软件自带的“auto.arima()”功能拟合的模型与冯丹等[4]利用我国1995年1月至2004年4月法定传染病报告数拟合的模型ARIMA(1,0,0)(1,1,0)12是一致的,但对该模型进一步进行残差白噪声检验时发现,该模型的残差检验在滞后6阶时P=0.268 6,滞后12阶时P=0.060 7较接近0.05(见表 1);王怡等[5]的研究也显示P值在滞后6阶时P=0.663 0,滞后12阶时P=0.071 8较接近0.05,滞后18阶时P=0.243 6,滞后24阶时P=0.243 0。根据Zheng等[20]发表的文献显示,残差检验P<0.8时模型对数据的拟合不够充分,一方面可能是因为时间选择上的差别:因为在不同的时间,我国法定传染病的条目可能会不同且疾病的传播模式随着时代的改变也在不断发生新的变化;另一方面是因为在使用时间序列模型进行预测时,其前提是研究对象要在一定的历史时期内保持相对的稳定,因此可能是现在的社会经济条件以及疾病传播模式与10年前相比发生了变化;再者可能是研究选取的数据偏少,导致数据中的规律未被充分的揭示出来,导致建模的结果与其他的研究结果不一致,所以本研究未引用他们的拟合模型;另外,ARIMA时间序列模型的选择很大程度是研究者依据ACF和PACF图再结合自己的经验综合确定的相对最优模型,所以研究者给出的模型并不一定是最优模型而是综合了研究者自身经验所做出的相对最优选择。此外,根据Anwar等[2]文献的启示,跳出p和q一般情况下小于5的限制尝试建立了几个可能的模型,发现ARIMA(7,1,0)(1,0,1)12有着更小的绝对误差和相对误差(平均值<5%),并且残差检验大于0.8提示拟合效果更好,因此再一次提示了研究者所拟合出的模型并不一定就是最优模型。值得一提的是这两个模型对2016年9月进行预测的相对误差发现ARIMA(4,1,0)(1,1,1)12的相对误差为9.78%、ARIMA(7,1,0)(1,0,1)12的相对误差为14.89%,且预测值均大于实际发生数。可能的原因是预测误差本身存在的影响,也可能是9月法定传染病实际发病数减少与某些原因有关,但具体原因还需要进一步研究。另外,本研究模型预测值的平均相对误差为5.39%,说明建立的模型的预测误差是可以接受的[21],模型可以用于预测。
随着循证思想的广泛传播,疾病防控也需要证据的支持尤其是全国性大数据证据的支持。本研究可为制定传染病防控策略和措施上提供较为科学的证据支持,尤其是在确定防控传染病的重点月份上,从时序图可以看出每年2月发病人数最低,从2-6月发病人数近乎呈直线增长,提示从2月开始在全国范围内加强传染病的监测、防范和宣教工作以增加人群防范传染病的意识减少人群发病人数,而6月之后传染病发病人数又开始呈现近似直线下降的趋势,在最后3个月报告人数又有上升的趋势,不过增幅不是很大但也应引起重视。本研究是以传染病月报告发病总数进行研究,在实际应用中还可以根据每种传染病的特点对具体传染病进行研究,即对专病的建模与预测[5]。对单一病种的预测或许能获得直接的公共卫生意义,但这种公共卫生意义是局限的,无法把握法定传染病的总体情况。但对全部传染病进行建模预测虽然能把握传染病的全貌但同样也有缺陷,因为即使能发现问题但在确定具体情况上仍需要花费时间。因此如果既可以建立各个传染病的ARIMA预测模型又可以建立全部传染病的ARIMA预测模型可能会是更合理的方法。
时间序列是随着时间推移而产生的一组随机序列,因为无法得知下一个时间点的数值,所以很少有一种模型可以一直进行预测,我们要随着时间的推移和新数据的不断引入而不断地调整已有的模型以达到最佳的预测效果。由于ARIMA模型的建立很大程度上会受到研究者知识水平的限制,因此对同一种疾病进行建模时可能会由于研究者不同而得出不同的模型,但最后的模型应该是基于研究者的经验和知识水平综合确定的。
利益冲突: 无
| [1] | Baer A, Libassi L, Lloyd JK, et al. Risk factors for infections in international travelers:An analysis of travel-related notifiable communicable diseases[J]. Travel Med Infect Dis, 2014, 12(5): 525–533. DOI:10.1016/j.tmaid.2014.05.005 |
| [2] | Anwar MY, Lewnard JA, Parikh S, et al. Time series analysis of malaria in Afghanistan:using ARIMA models to predict future trends in incidence[J]. Malar J, 2016, 15(1): 566. DOI:10.1186/s12936-016-1602-1 |
| [3] |
张妍. 天津市某区2000-2013年传染病流行特征的研究[D]. 天津: 天津医科大学, 2014.
Zhang Y. The epidemic characteristics of communicable diseases in a district of Tianjin from 2000 to 2013[D]. Tianjin:Tianjin Medical University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10062-1014350016.htm |
| [4] |
冯丹, 韩晓娜, 赵文娟, 等.
中国内地法定报告传染病预测和监测的ARIMA模型[J]. 疾病控制杂志, 2007, 11(2): 140–143.
Feng D, Han XN, Zhao WJ, et al. Using ARIMA model to surveillance and forecast the incidence rate of notifiable infectious diseases in Mainland China[J]. Chin J Dis Control Prev, 2007, 11(2): 140–143. DOI:10.3969/j.issn.1674-3679.2007.02.008 |
| [5] |
王怡, 张震, 范俊杰, 等.
ARIMA模型在传染病预测中的应用[J]. 中国预防医学杂志, 2015, 16(6): 424–428.
Wang Y, Zhang Z, Fan JJ, et al. Application of ARIMA model in the forecasting of infectious disease[J]. Chin Prev Med, 2015, 16(6): 424–428. DOI:10.16506/j.1009-6639.2015.06.008 |
| [6] |
国家卫生和计划生育委员会. 疫情播报[EB/OL]. (2016). [2017-04-21]. http://www.moh.gov.cn/zwgk/yqbb3/ejlist.shtml. commission of the PRC.
Epidemic Broadcast. National health and family planning commission of the PRC. Epidemic Broadcast[EB/OL].(2016).[2017-04-21]. http://www.moh.gov.cn/zwgk/yqbb3/ejlist.shtml.commission of the PRC. Epidemic Broadcast. |
| [7] | Zeng QL, Li DD, Huang G, et al. Time series analysis of temporal trends in the pertussis incidence in Mainland China from 2005 to 2016[J]. Sci Rep, 2016, 6: 32367. DOI:10.1038/srep32367 |
| [8] |
国家卫生和计划生育委员会. 国家卫生计生委关于调整部分法定传染病病种管理工作的通知[EB/OL]. (2013-11-04)[2017-04-21] http://www.nhfpc.gov.cn/jkj/s3577/201311/f6ee56b5508a4295a8d552ca5f0f5edd.shtml.
The notice of adjusting some legal infectious diseases' management of the National Health and Family Planning Commission of the PRC National Health and Family Planning Commission of the PRC[EB/OL].(2013-11-04)[2017-04-21]. http://www.nhfpc.gov.cn/jkj/s3577/201311/f6ee56b5508a4295a8d552ca5f0f5edd.shtml. The notice of adjusting some legal infectious diseases' management of the National Health and Family Planning Commission of the PRC. |
| [9] |
王燕.时间序列分析——基于R[M]. 北京: 中国人民大学出版社, 2015.
Wang Y.Time series analysis with R[M]. Beijing: China Renmin University Press, 2015. |
| [10] |
王燕.应用时间序列分析[M]. 4版. 北京: 中国人民大学出版社, 2015.
Wang Y.Applied time series analysis[M]. 4th ed. Beijing: China Renmin University Press, 2015. |
| [11] |
刘峰, 朱妮, 邱琳, 等.
ARIMA乘积季节模型在陕西省手足口病预测中的应用[J]. 中华流行病学杂志, 2016, 37(8): 1117–1120.
Liu F, Zhu N, Qiu L, et al. Application of R-based multiple seasonal ARIMA model, in predicting the incidence of hand, foot and mouth disease in Shaanxi province[J]. Chin J Epidemiol, 2016, 37(8): 1117–1120. DOI:10.3760/cma.j.issn.0254-6450.2016.08.013 |
| [12] | Song X, Xiao J, Deng J, et al. Time series analysis of influenza incidence in Chinese provinces from 2004 to 2011[J]. Medicine (Baltimore), 2016, 95(26): e3929. DOI:10.1097/MD.0000000000003929 |
| [13] | Lin YL, Chen M, Chen GW, et al. Application of an autoregressive integrated moving average model for predicting injury mortality in Xiamen, China[J]. BMJ Open, 2015, 5(12): e8491. DOI:10.1136/bmjopen-2015-008491 |
| [14] | Cesar SR. Disease management with ARIMA model in time series[J]. Einstein, 2013, 11(1): 128–131. DOI:10.1590/S1679-45082013000100024 |
| [15] | Brownson R C.Evidence-based public health[M]. Beijing: Peking Union Medical College Press, 2012. |
| [16] | Kane MJ, Price N, Scotch M, et al. Comparison of ARIMA and Random Forest time series models for prediction of avian influenza H5N1 outbreaks[J]. BMC Bioinform, 2014, 15: 276. DOI:10.1186/1471-2105-15-276 |
| [17] | Guo C, Yang J, Guo YM, et al. Short-term effects of meteorological factors on pediatric hand, foot, and mouth disease in Guangdong, China:a multi-city time-series analysis[J]. BMC Infect Dis, 2016, 16(1): 524. DOI:10.1186/s12879-016-1846-y |
| [18] | Zhang XY, Hou FS, Qiao ZJ, et al. Temporal and long-term trend analysis of class C notifiable diseases in China from 2009 to 2014[J]. BMJ Open, 2016, 6(10): e11038. DOI:10.1136/bmjopen-2016-011038 |
| [19] |
易燕飞. 基于时间序列模型的传染病流行趋势及预测研究[D]. 长春: 长春工业大学, 2016.
Yi YF. Epidemic prediction of infectious diseases based on time series model[D]. Changchun:Changchun University of Technology, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10190-1016759377.htm |
| [20] | Zheng YL, Zhang LP, Zhang XL, et al. Forecast model analysis for the morbidity of tuberculosis in Xinjiang, China[J]. PLoS One, 2015, 10(3): e116832. DOI:10.1371/journal.pone.0116832 |
| [21] |
耿娟.
ARIMA模型在医院门诊量预测中的应用[J]. 中国卫生统计, 2014, 31(4): 643–645.
Geng J. The application of ARIMA model in forecasting the amount of outpatient[J]. Chin J Health Stat, 2014, 31(4): 643–645. |
 2017, Vol. 38
2017, Vol. 38