文章信息
- 翁鸿, 林恩萱, 童铁军, 万翔, 耿培亮, 曾宪涛.
- Weng Hong, Lin Enxuan, Tong Tiejun, Wan Xiang, Geng Peiliang, Zeng Xiantao.
- 遗传关联性研究Meta分析之遗传模型的选择:贝叶斯无基因模型法
- Choice of genetic model on Meta-analysis of genetic association studies: introduction of genetic model-free approach for Bayesian analysis
- 中华流行病学杂志, 2017, 38(12): 1703-1707
- Chinese journal of Epidemiology, 2017, 38(12): 1703-1707
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2017.12.024
-
文章历史
收稿日期: 2017-05-31
2. 中国香港浸会大学数学系统计学研究及咨询中心;
3. 中国香港浸会大学计算机系
2. Statistics Research and Consultancy Centre, Department of Mathematics, Hong Kong Baptist University, Hong Kong;
3. Department of Computer Science, Hong Kong Baptist University, Hong Kong
与随机对照试验的Meta分析相比,20世纪90年代遗传关联性研究的Meta分析才应用到研究领域。近年来,关于遗传关联性研究Meta分析的研究受到越来越多的学者关注,其研究数量也急剧增长。前期对该主题方法学方面进行了相关介绍[1-4],包括异质性、哈迪-温伯格平衡以及多重检验校正等。但关于遗传模型的选择问题,国内尚无关于此主题的讨论。
遗传关联性研究中以单核苷酸多态性(single nucleotide polymorphism,SNP)最为常见,而SNP中以2个等位基因变异最为常见,此时就产生了3种基因型。这3种基因型可产生多种遗传模型,而常用的主要有4种:等位基因模型(allele model)、共显性模型(co-dominant model)、隐性模型(recessive model)、显性模型(dominant model),其中共显性模型包括纯合子模型(homozygote model)和杂合子模型(heterozygote model)[5-8]。在涉及SNP数据的Meta分析时,大多数研究者会同时计算出这些模型,这不仅增加了假阳性的风险,也使得读者难以进一步解读结果。因此,在进行基因关联研究的Meta分析时,首先应合理地选择遗传模型。本文主要介绍使用贝叶斯理论的无基因模型法(genetic model-free approach)。
一、无基因模型法的基本原理1.基因模型分类:基因关联研究Meta分析与传统二分类Meta分析的不同之处在于基因关联研究有至少3个基因型,且这3种基因型并不是独立存在的,而是由遗传模型将这三者联系起来。以二等位基因为例,假设等位基因A突变为B,则AA为野生纯和子,AB为杂合子,BB为突变纯合子。常用的基因模型:等位基因模型(B vs. A)、纯合子模型(BB vs. AA)、杂合子模型(AB vs. AA)、显性模型(BB+AB vs. AA)和隐性模型(BB vs. AA+AB);等位基因模型也称为积性模型(multiplicative model)。此外,还有2种模型较少使用,加性模型(additive model,BB vs. AB vs. AA)和超显性模型(over-dominant model,AB vs. AA+BB),加性模型主要在原始研究中使用,可采用Armitage’s趋势检验;而超显性模型这种遗传模型在现实中很少见,即杂合子优势。
2.无基因模型法:将野生纯合子AA基因型作为参照组可以得到两个比值比(OR):ORAB和ORBB,ORAB是AB基因型与AA基因型比较的OR值,ORBB为BB基因型与AA基因型比较的OR值。而这两个OR值通过遗传模型相互关联,不能忽视它们之间的相关性。但是大多数基因的遗传模型我们并不清楚,因此有研究者提出了放弃假设遗传模型,但考虑ORAB和ORBB的关联。该模型引入参数λ,将logORAB视为一个未知的比例,并定义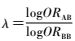
Minelli等[6]提出的贝叶斯无基因模型法有两种函数方法,包括回顾性似然函数法(retrospective likelihood)和前瞻性似然函数法(prospective likelihood)。回顾性似然函数法从暴露因素入手,基因型作为暴露因素时,以二等位基因为例,就有3个基因型。与回顾性似然函数法相反,前瞻性似然函数法从结果变量(即疾病状态)入手,为二分类变量。在一些情况下二者的计算结果相近,但回顾性似然函数法便于理解。因此本文主要介绍回顾性似然函数法。
定义j为基因型(j=1、2、3分别代表AA、AB、BB基因型),d为疾病状态(d=0、1分别为对照组、病例组),y0j和y1j分别为j基因型中对照组和病例组的事件数,n0和n1分别代表对照组和病例组的样本量,Meta分析中每个纳入研究的回顾性似然函数(LR)可通过以下多项式分布得到:y0j~Multinominal(n0,p0j);y1j~Multinominal(n1,p1j)。
病例组和对照组暴露于j基因型的概率为pdj=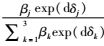

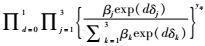
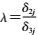
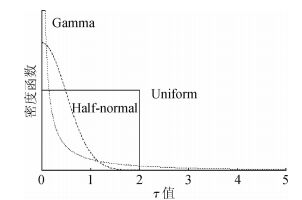
1.异质性的先验分布:研究间标准差(standard deviation,τ)考虑3种分布,分别为γ分布(Gamma distribution)、半正态分布(half-normal distribution)和均匀分布(uniform distribution)。见图 1。
|
| 图 1 研究间标准差τ的先验分布概率 |
第一种先验分布为精度的γ分布: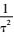

第二种先验分布为标准差τ的标准半正态分布:τ~Half-normal(0,1),τ>0。在x=0(即y轴)处截断,若标准差的值超过2时,该分布给出的概率较低。第三种分布为0~2的均匀分布:τ~Uniform(0,2),该分布排除了标准差超过2的概率。
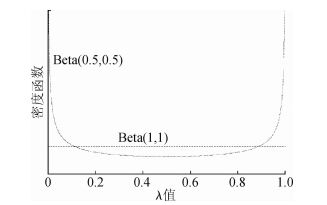
2.参数λ的先验分布:参数λ有两种β分布(Beta distribution),这两种β分布都限制在0~1之间,且这两种分布已被用于模拟比例的先验分布。见图 2。
|
| 图 2 参数λ的两种先验分布概率 |
第一种β分布的参数均定义为1:λ~β(1,1)。该分布在0~1之间均匀分布。然而当参数值λ趋近于极端值(0或1),且数据稀疏,此时该分布会将后验分布估计值推向0.5,这可能会导致研究者选择错误的遗传模型。第二种β分布的参数均定义为0.5:λ~β(0.5,0.5),与一种二项式似然的先验分布一致。当参数值λ趋近于极端值时,该分布会给予其较大的先验概率,即使遗传模型趋向于隐性或显性模型;但当遗传模型为共显性模型(即参数λ=0.5),且数据较为稀疏时,该分布会增大参数λ的不确定性。
三、实例分析以Kato等[12]发表的血管紧张素原基因M235T多态性与原发性高血压发病风险相关性的Meta分析为例,见表 1。
采用OpenBugs软件计算参数λ建模:
model{
for(i in 1:7){
p[i,1]<-1/(1+b[i,1]+b[i,2])
p[i,2]<-b[i,1]/(1+b[i,1]+b[i,2])
p[i,3]<-b[i,2]/(1+b[i,1]+b[i,2])
q[i,1]<-1/(1+b[i,1]*exp(lambda*d[i])+b[i,2]*exp(d[i]))
q[i,2]<-b[i,1]*exp(lambda*d[i])/
(1+b[i,1]*exp(lambda*d[i])+b[i,2]*exp(d[i]))
q[i,3]<-b[i,2]*exp(d[i])/
(1+b[i,1]*exp(lambda*d[i])+b[i,2]*exp(d[i]))
d[i]~dnorm(theta,tau2)
ncont[i,1:3]~dmulti(p[i,1:3],tcont[i])
ncase[i,1:3]~dmulti(q[i,1:3],tcase[i])
b[i,1]~dnorm(0,0.0001)
b[i,2]~dnorm(0,0.0001)
}
lambda~dbeta(1,1)
theta~dnorm(0,0.0001)
tau2~dgamma(0.001,0.001)
OR1<-exp(theta)
OR2<-exp(lambda*theta)
SD<-1/sqrt(tau2)
}
list(ncase=structure(.Data=c(2,20,83,3,17,62,3,30,31,5,23,52,8,39,133,6,34,68,20,214,483),.Dim=c(7,3)),ncont=structure(.Data=c(3,34,44,4,30,49,17,84,48,5,32,63,12,62,119,9,48,47,18,134,363),.Dim=c(7,3)),
tcase=c(105.000,82.000,64.000,80.000,180.000,108.000,717.000),
tcont=c(81.000,83.000,149.000,100.000,193.000,104.000,515.000))
list(lambda=0.5,theta=0,tau2=1,b=structure(.Data=c(0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5),.Dim=c(7,2)))
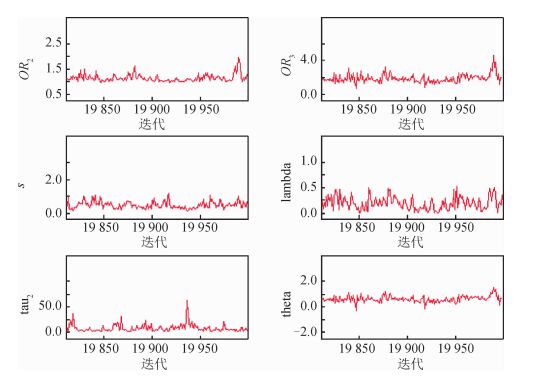
上述命令运行后,得到Gibbs抽样图(图 3)、迭代历史图(图 4)和后验分布概率估计图(图 5)。
|
| 图 3 Gibbs抽样图 |
|
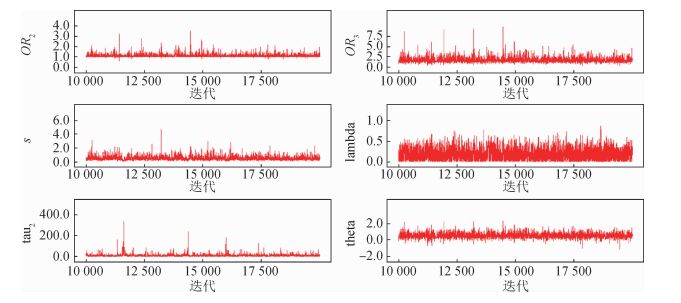
| 图 4 迭代历史图 |
|
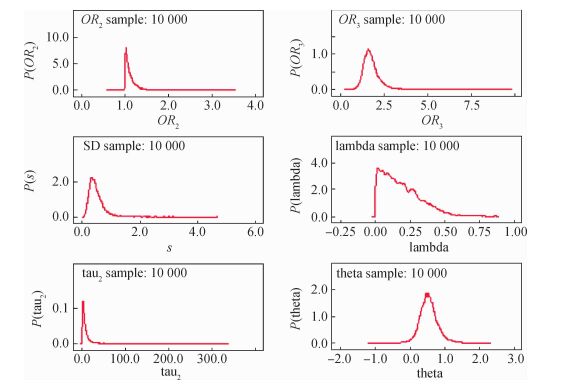
| 图 5 后验分布概率估计图 |
此外,所得各参数结果见表 2,参数λ为0.181 7,OR1=1.777为TT vs. MM的OR值,OR2=1.118为TT vs. MT的OR值。对于基因模型的选择,λ接近与0,因此,宜选择隐性基因模型来估计M235T多态性与原发性高血压的发病风险相关性。此外,采用传统Meta分析方法的结果显示:ORTT vs.MM=1.61、ORTT vs. MT=1.29,由λ计算公式,可得传统Meta分析方法所得的参数λ结果为1.248 1。与贝叶斯无基因模型法的结果相比,传统Meta分析方法所得结果可能会高估λ参数。
在没有外部可用信息的情况下,为避免多重比较,以及不能忽略各基因型间的关联性,贝叶斯无基因模型法采用贝叶斯理论,给出3个参数的模糊先验分布,然后模拟出参数的后验分布,推算出相应的参数值,并通过参数λ来选择相应的遗传模型。虽然该方法理念较为先进,但因为贝叶斯理论的使用需要涉及到WinBUGS软件或OpenBUGS软件[13],而这类软件需要进行建模等复杂操作,导致实际操作起来较为复杂,可能会限制该方法的使用。此外,此方法需要先验估计参数,因此,对于参数分布的估计不同可能会造成不同的结果。
利益冲突: 无
| [1] |
翁鸿, 李妙竹, 耿培亮, 等.
遗传关联性研究及其Meta分析的简介[J]. 中国循证心血管医学杂志, 2016, 8(10): 1156–1158.
Weng H, Li MZ, Geng PL, et al. Brief introduction of genetic association studies and corresponding Meta-analysis[J]. Chin J Evid Based Cardiovasc Med, 2016, 8(10): 1156–1158. DOI:10.3969/j.issn.1674-4055.2016.10.02 |
| [2] |
翁鸿, 张永刚, 牛玉明, 等.
遗传关联性研究Meta分析的多重检验校正方法[J]. 中国循证心血管医学杂志, 2016, 8(12): 1409–1411.
Weng H, Zhang YG, Niu YM, et al. Methods of multiple testing adjustments in Meta-analysis of genetic association study[J]. Chin J Evid Based Cardiovasc Med, 2016, 8(12): 1409–1411. DOI:10.3969/j.issn.1674-4055.2016.12.01 |
| [3] |
阮晓岚, 翁鸿, 田国祥, 等.
遗传关联性研究Meta分析的异质性来源[J]. 中国循证心血管医学杂志, 2016, 8(9): 1025–1028.
Ruan XL, Weng H, Tian GX, et al. Source of heterogeneity in Meta-analysis of genetic association studies[J]. Chin J Evid Based Cardiovasc Med, 2016, 8(9): 1025–1028. DOI:10.3969/j.issn.1674-4055.2016.09.01 |
| [4] |
翁鸿, 江梅, 仇成凤, 等.
遗传关联性研究Meta分析中的Hardy-Weinberg平衡[J]. 中国循证心血管医学杂志, 2016, 8(11): 1281–1283, 1287.
Weng H, Jiang M, Qiu CF, et al. Hardy-Weinberg equilibrium in Meta-analysis of genetic association study[J]. Chin J Evid Based Cardiovasc Med, 2016, 8(11): 1281–1283, 1287. DOI:10.3969/j.issn.1674-4055.2016.11.01 |
| [5] | Lewis CM. Genetic association studies:design, analysis and interpretation[J]. Brief Bioinform, 2002, 3(2): 146–153. DOI:10.1093/bib/3.2.146 |
| [6] | Minelli C, Thompson JR, Abrams KR, et al. Bayesian implementation of a genetic model-free approach to the Meta-analysis of genetic association studies[J]. Stat Med, 2005, 24(24): 3845–3861. DOI:10.1002/sim.2393 |
| [7] | Minelli C, Thompson JR, Abrams KR, et al. The choice of a genetic model in the Meta-analysis of molecular association studies[J]. Int J Epidemiol, 2005, 34(6): 1319–1328. DOI:10.1093/ije/dyi169 |
| [8] | Thakkinstian A, McElduff P, D'Este C, et al. A method for Meta-analysis of molecular association studies[J]. Stat Med, 2005, 24(9): 1291–1306. DOI:10.1002/sim.2010 |
| [9] | Gelman A. Prior distributions for variance parameters in hierarchical models (comment on article by Browne and Draper)[J]. Bayesian Anal, 2006, 1(3): 515–533. DOI:10.1214/06-BA117A |
| [10] | Lambert PC, Sutton AJ, Burton PR, et al. How vague is vague? A simulation study of the impact of the use of vague prior distributions in MCMC using WinBUGS[J]. Stat Med, 2005, 24(15): 2401–2428. DOI:10.1002/sim.2112 |
| [11] | Kass RE, Wasserman L. The selection of prior distributions by formal rules[J]. J Am Stat Assoc, 1996, 91(435): 1343–1370. DOI:10.1080/01621459.1996.10477003 |
| [12] | Kato N, Sugiyama T, Morita H, et al. Angiotensinogen gene and essential hypertension in the Japanese:extensive association study and Meta-analysis on six reported studies[J]. J Hypertens, 1999, 17(6): 757–763. DOI:10.1097/00004872-199917060-00006 |
| [13] |
董圣杰, 冷卫东, 田家祥, 等.
Meta分析系列之五:贝叶斯Meta分析与WinBUGS软件[J]. 中国循证心血管医学杂志, 2012, 4(5): 395–398.
Dong SJ, Leng WD, Tian JX, et al. Fifth part of series of Meta-analysis:Bayesian Meta-analysis and WinBUGS software[J]. Chin J Evid Based Cardiovasc Med, 2012, 4(5): 395–398. DOI:10.3969/j.issn.1674-4055.2012.05.002 |
 2017, Vol. 38
2017, Vol. 38




