文章信息
- 宋秋月, 伍亚舟.
- Song Qiuyue, Wu Yazhou.
- 纵向数据潜变量增长曲线模型及其在Mplus中的实现
- The latent variable growth curve model of longitudinal data and its implementation in Mplus
- 中华流行病学杂志, 2017, 38(8): 1132-1135
- Chinese journal of Epidemiology, 2017, 38(8): 1132-1135
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2017.08.027
-
文章历史
收稿日期: 2016-12-21
随着精准医学和大数据概念的提出,流行病学大型队列研究的运用越来越广泛,同时产生了大量复杂的纵向数据(longitudinal data)。这些数据具有时间序列性、高维性、自相关性、多元性及易缺失等特性,且包含着复杂的横向和纵向关系。传统的纵向数据处理方法(如协方差分析、重复测量资料方差分析)只注重总体的发展趋势,即数据的纵向关系,难以对资料信息做出合理解释。潜变量增长曲线模型(latent variable growth curve model,LGCM)是在结构方程模型基础上发展演变而来,能够比较总体发展趋势和个体变化的差异,在含有潜变量的纵向数据中使用极为广泛[1-3]。目前Mplus软件分析处理LGCM十分普遍,操作方便,功能强大[4]。为此本文通过实例探讨纵向数据LGCM的分析方法,并提供含有潜变量的纵向数据在Mplus中的实现过程和程序。
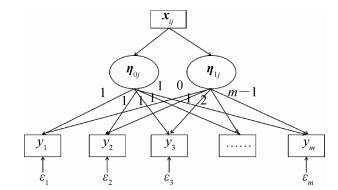
基本原理LGCM源于探索性因子分析及相关文献,是结构方程模型的一种变式。可以分析某一变量的变化趋势,用不可测量或难以测量的潜变量来描述总体的平均增长趋势,还可分析总体发展趋势和总体之间存在的差异,也可以分析个体之间的发展差异[5]。LGCM与含有均值的结构方程模型类似,是将截距η0j和斜率η1j定义为潜在因素,以描述纵向数据的变化特征。如图 1中y1、y2、y3、ym分别表示m次重复测量,ε1、ε2、ε3、εm表示每次测量误差,LGCM中2个潜在因子是截距因子η0j和斜率因子η1j。截距因子表示观察对象测量的初始水平,描述当时间变量等于0时,结果变量y的水平,是常数项,不考虑协变量;斜率因子表示观察对象的增长轨迹,合适的载荷因子有利于模型参数的解释。截距η0j到m次观测的载荷均定义为1,斜率η1j的因子载荷称为时间分值,斜率η1j到m次观测的载荷(at-a)定义为0,1,……,m-1,也可自由定义,以减少自由度。
|
| 注:xij为时间恒定的协变量,y1、y2、y3、ym分别表示m次重复测量,ε1、ε2、ε3、εm表示每次测量误差,η0j为截距因子,η1j为斜率因子 图 1 潜变量增长曲线模型 |
1.简单非条件潜变量增长曲线模型:即不考虑任何协变量,其模型为
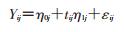 (1)
(1)
 (2)
(2)
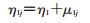 (3)
(3)
式中Yij表示第i个观察单位在第j个时间点的测量值;tij表示测量次数;η0j表示截距即个体的初始状态;η1j表示斜率即个体发展变化速度;εij是观察单位个体内的结局变量测量的随机误差;η0是截距的均值,表示所有个体在第一次观测时总体均值的估计;η1表示斜率的平均值;μ0j表示第一次观测时个体间的差异;μ1j表示不同个体斜率变化的变异。非条件潜变量增长曲线模型与结构方程模型类似,可以用结构方程模型对其进行参数估计和评估方程拟合效果[6]。
2.条件潜变量曲线增长模型:在非条件潜变量增长曲线模型的基础上纳入协变量,用以预测截距因子和斜率因子。协变量又分为时间恒定和时间变化两种情况。
(1) 时间恒定协变量的LGCM:其模型为
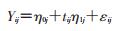 (4)
(4)
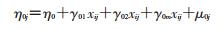 (5)
(5)
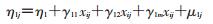 (6)
(6)
式中xij表示时间恒定的协变量;γ01表示协变量对截距的影响;γ11表示协变量对斜率的影响,即协变量与时间的交互作用。
(2) 时间变化的LGCM:其模型为
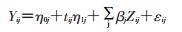 (7)
(7)
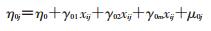 (8)
(8)
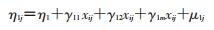 (9)
(9)
式中时间变化协变量Zij表示重复测量j次用于预测时间点上的结局变量Yij;βj表示协变量对结局变量的影响大小。
3. Mplus软件实现:Mplus主要包含10个常用命令,即TITLE、DATA、VARIABLE、DEFINE、ANALYSIS、MODEL、OUTPUT、SAVEDATA、PLOT、MONTECARLO[7]。本文使用Mplus 7.0软件进行编程,非条件和条件潜变量增长曲线模型分析纵向数据的Mplus程序见表 1。
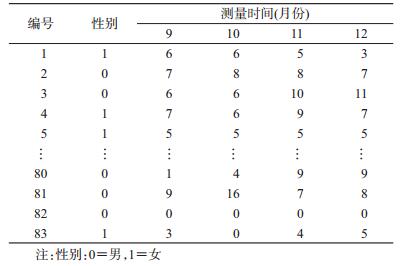
1.资料数据:该研究采用自制量表监测大学生心理健康状况,每隔1个月进行测量,该量表含有“感觉紧张不安”等5个条目以及“是否有自杀想法”1个特殊条目,每个条目有5个选项:0=完全没有,1=轻微,2=中等程度,3=厉害,4=非常厉害,得分越高表示心理压力越大,需要给予适当干预。共观测了83名学生一学期4次的心理测评情况,其中男生29人,女生54人,结果见表 2。
2.结果分析:
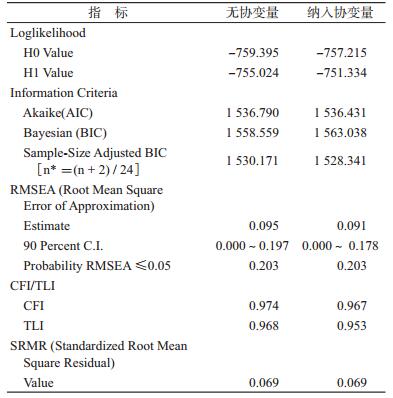
(1) 模型拟合情况:根据Mplus输出结果显示,无协变量情况下,χ2=8.743,P>0.05,模型拟合良好,近似误差均方根RMSEA=0.095>0.08,拟合结果可接受,但不理想。比较拟合指数CFI=0.974,TLI=0.968,均>0.95,标准化拟合残差SRMR=0.069,表示拟合效果好。协变量的引入可以提高模型的拟合效果,模型χ2=11.763,P>0.05,模型拟合效果良好,近似误差均方根RMSEA=0.091,较前者更接近可接受界值。比较拟合指数CFI=0.967,TLI=0.953,也均>0.95,标准化拟合残差SRMR=0.069(<0.08表示拟合效果好),结果见表 3。
(2) 非条件潜变量增长曲线模型结果分析:截距均值为4.475,斜率均值为0.048,学生心理评分随时间变化呈上升趋势。潜变量的方差估计结果显示,截距的方差为4.632,P<0.05,斜率的方差为0.518,P<0.05,差异有统计学意义,说明心理健康状况的初始水平和变化趋势存在个体差异。截距与斜率的协方差为-0.285,说明截距与斜率呈负相关关系,P=0.461,差异无统计学意义,说明心理健康状况的初始水平与变化速度相关不显著(表 4)。
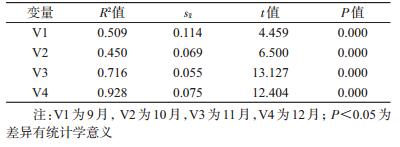
决定系数是响应变量总变异中能被潜变量因子解释的比例,其值等于标准化因子负荷的平方,结果显示V3(11月)和V4(12月)测量的决定系数较大,且均P<0.05,差异有统计学意义(表 5)。
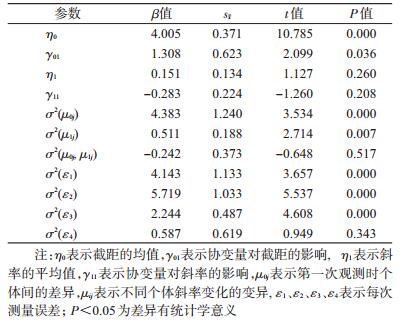
(3) 时间恒定潜变量增长曲线模型:在非条件潜变量增长曲线模型的基础上纳入性别协变量,探讨性别对大学生心理健康状况变化的影响。结果显示,η0=4.005,为大学生心理评分的初始水平均值,η1=0.151,为大学生心理评分平均变化趋势。σ2(μ0j)=4.383,σ2(μ1j)=0.511,均P<0.05,说明心理健康状况的初始水平和变化趋势存在个体差异,γ01=1.308,P<0.05,γ11=-0.283,P>0.05,分别是性别对截距和斜率的影响,不同性别的学生的心理评分初始水平不同,变化趋势不受性别影响(表 6)。
众多的纵向数据分析处理方法各有优缺,如重复测量方法分析注重总体的发展趋势,不能分析个体发展的差异,而且无法处理数据中存在缺失值的情况。多层线性模型能够较好地处理有缺失值的纵向数据,但是对于参数的估计其方法复杂,不能测量结局变量与潜变量的关系[8]。本文采用LGCM的两种类型分析大学生心理健康状况,结果显示初始水平和变化趋势存在个体差异,不同性别学生的心理评分初始水平不同,变化趋势不受性别影响。纳入协变量的条件潜变量增长曲线模型拟合效果更好,但参数较多,建模复杂,因此在后续研究中将探讨不同模型对纵向数据的分析处理及其效果评价。
本文实例中针对大学生心理健康状况提供了纵向数据LGCM的Mplus实现程序,其编程语言简单易学、操作方便,且软件更新速度快,计算方法丰富,能分析处理含有潜变量的纵向数据,为流行病学队列研究中统计学方法的应用提供参考。
利益冲突: 无
| [1] |
刘红云, 孟庆茂.
纵向数据分析方法[J]. 心理科学进展, 2003, 11(5): 586–592.
Liu HY, Meng QM. A review on longitudinal data analysis method and it's development[J]. Adv Psychol Sci, 2003, 11(5): 586–592. DOI:10.3969/j.issn.1671-3710.2003.05.019 |
| [2] |
李丽霞, 周舒冬, 张敏, 等.
多水平模型和潜变量增长曲线模型在纵向数据分析中的应用及比较[J]. 中华流行病学杂志, 2014, 34(6): 741–744.
Li LX, Zhou SD, Zhang M, et al. Comparisons of two statistical approaches in studying the longitudinal data:the multilevel model and the latent growth curve model[J]. Chin J Epidemiol, 2014, 34(6): 741–744. DOI:10.3760/cma.j.issn.0254-6450.2014.06.028 |
| [3] | Verbeke G, Fieuws S, Molenberghs G, et al. The analysis of multivariate longitudinal data:a review[J]. Stat Methods Med Res, 2014, 23(1): 42–59. DOI:10.1177/0962280212445834 |
| [4] | Gunzler DD, Morris N. A tutorial on structural equation modeling for analysis of overlapping symptoms in co-occurring conditions using Mplus[J]. Stat Med, 2015, 34(24): 3246–3280. DOI:10.1002/sim.6541 |
| [5] |
李丽霞, 郜艳晖, 张敏, 等.
潜变量增长曲线模型及其应用[J]. 中国卫生统计, 2012, 29(5): 713–716.
Li LX, Gao YH, Zhang M, et al. Latent growth curves model and its application[J]. Chin J Health Stat, 2012, 29(5): 713–716. |
| [6] |
王济川, 王小倩, 姜宝法.结构方程模型:方法与应用[M]. 北京: 高等教育出版社, 2011.
Wang JC, Wang XQ, Jiang BF.Structural equation models:methods and applications[M]. Beijing: Higher Education Press, 2011. |
| [7] |
裴磊磊, 任琳, 张岩波, 等.
Mplus软件简介[J]. 中国卫生统计, 2013, 30(4): 614–616.
Pei LL, Ren L, Zhang YB, et al. Mplus software profile[J]. Chin J Health Stat, 2013, 30(4): 614–616. |
| [8] |
高彩虹. 基于广义估计方程和潜变量增长曲线模型的阿尔茨海默病健康相关生命质量动态变化研究[D]. 太原: 山西医科大学, 2012.
Gao CH. Dynamic study on health-related quality of life in the progression of Alzheimer's disease based on generalized estimating equations and latent growth curve model[D]. Taiyuan:Shanxi Medical University, 2012. http://d.wanfangdata.com.cn/Thesis/Y2127550 |
 2017, Vol. 38
2017, Vol. 38