文章信息
- 王德征, 王冲, 沈成凤, 张颖, 张辉, 宋桂德, 薛晓丹, 徐忠良, 张爽, 江国虹.
- Wang Dezheng, Wang Chong, Shen Chengfeng, Zhang Ying, Zhang Hui, Song Guide, Xue Xiaodan, Xu Zhongliang, Zhang Shuang, Jiang Guohong.
- Cochran-Armitage趋势检验和线性回归在流行病学率的趋势分析中的比较研究
- omparison of application of Cochran-Armitage trend test and linear regression analysis for rate trend analysis in epidemiology study
- 中华流行病学杂志, 2017, 38(5): 684-687
- Chinese Journal of Epidemiology, 2017, 38(5): 684-687
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2017.05.026
-
文章历史
收稿日期: 2016-09-30
在某地区的疾病监测中,经常可以得到不同年份某种疾病的患病、发病或死亡情况,这些情况通常使用疾病事件在人群中出现的频率加以描述。为了统计随着年份的变化,某种疾病率的变化是否存在某种趋势,并且检验这种趋势是否具有统计学意义,就要用到率的趋势分析。本文利用1999-2013年天津市居民急性心肌梗死(AMI)发病率的时间趋势分析为例,采用Cochran-Armitaget趋势(Cochran-Armitage trend,CAT)检验即通常所说的趋势χ2检验(Chi-square test for trend)和线性回归两种方法进行率的时间趋势分析,比较两种统计学方法结果的差异并分析其原因。以期对这类流行病学资料如何正确的运用统计学方法,全面地描述疾病的变化趋势提供依据。
基本原理1. CAT检验:以William Cochran和Peter Armitage命名的CAT检验,一般用来评估一个二分类变量和一个有序分类变量关联性的统计方法,即k×2列联表资料的关联性分析。就是说,在率的时间趋势分析中,利用CAT检验分析有序分类变量各水平组的发生率是否随着水平数值或程度的增大或减小呈上升或下降的趋势[1]。CAT检验计算公式:
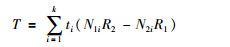
式中,ti代表权重,N1iR2-N2iR1的差异可以看成是对行调整后使其具有相同总数后的N1i和N2i的差异。当频率随着k可能有单调的变化趋势时,权重ti经常进行运算,具体赋值根据研究目的不同而不同。例如,当我们要研究频率的线性趋势时,ti应该被赋值为(0,1,2),当我们要研究k=3组与k=1,2组频率不同,k=1和k=2组频率相同时,ti应该被赋值为(1,1,0)。
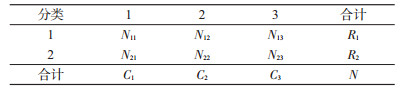
k×2列联表如下(以k=3为例):
如果期望的趋势是正确的,CAT检验相对于Pearson χ2检验有更高的效能,其检验统计量的计算公式:
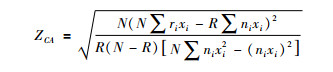
式中,N为各年份人口数的合计;R为各年份率的分子(病例数)的合计;ri为第i年的病例数;ni为第i年的人口数;xi为年份赋值(1,2,3…),可见其统计效能与率的原始频数即病例数和人口数以及年份的多少密切相关。
2.线性回归分析:假定在每个时间分割点有稳定的发生率,率的每年稳定的改变是基于率自然对数的线性模型[2],即率的时间趋势分析中,采用以率的自然对数作为因变量的线性回归模型,用回归模型的回归系数β来估计率的随时间变化的趋势是否具有统计学意义。其检验统计量的计算公式:
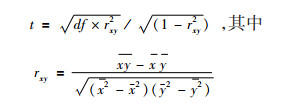
式中,rxy为因变量y(率值或其变换)与自变量x(年份)的相关系数,df为自由度。可见其统计效能与率值的点数即年份的多少密切相关。
利用β可估算出年度变化百分比(annual percent change,APC)。零假设为APC=0,即率的时间趋势没有变化。则关于APC的假设检验可通过检验回归系数β来实现。具体做法[3]:Y为因变量,Y=ln(ri),表示率的自然对数,Xi可以是年份或者年份段的组中值。由因变量和自变量构成的线性模型公式为Y=α+βX+ε。α为常数项,β为回归系数,ε为随机误差项。用回归系数β估计的APC公式为APC=100×(eβ-1),APC是否具有统计学意义通过估计β是否具有统计学意义来实现。
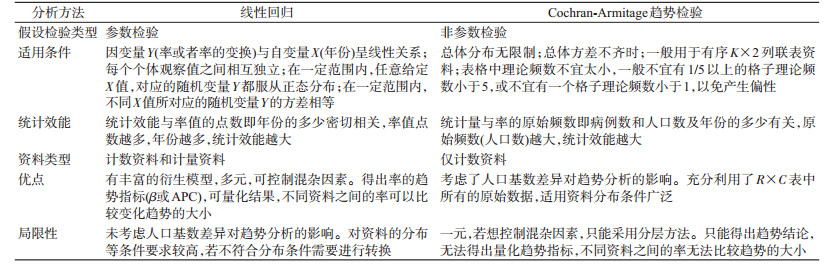
3.两种方法的适用性及优缺点:见表 1。
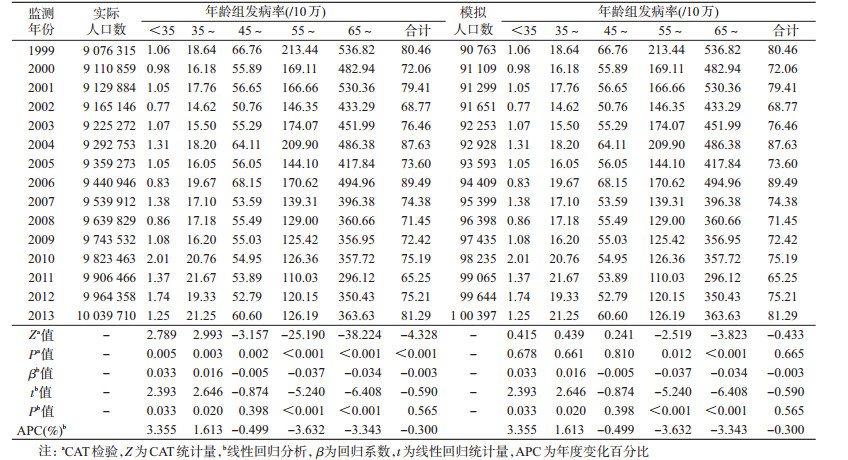
1.资料来源:资料采用覆盖天津市全人口的1999-2013年急性心肌梗死(AMI)发病率的数据为例,进行统计学分析。
2.研究方法:在保证AMI发病率不变的前提下,分别以实际人口规模和缩小100倍的人口规模为基础,对AMI发病率进行CAT检验和线性回归,比较不同样本量(人口规模)、分析方法对趋势分析结果的影响。CAT检验、线性回归分析及APC估计采用SAS 8.1软件,统计学检验以P<0.05为差异有统计学意义,采用双侧检验。
3.结果:1999-2013年天津市不同人口大小条件下AMI的发病率的CAT检验和线性回归的结果可以看出,无论是总发病率还是分年龄组发病率,CAT检验的P值均小于线性回归的P值,甚至个别发病率的时间趋势在CAT检验有统计学意义,但是在线性回归无统计学意义。见表 2。
将天津市的实际人口缩小100倍,AMI发病率保持不变,重新统计AMI发病率的时间趋势。可以看出,相对实际人口,缩小人口规模后的模拟人口AMI发病率的CAT检验P值呈明显升高,部分年龄组在实际人口的CAT检验中有统计学意义,缩小人口规模后得出P值无统计学意义。与此同时,线性回归的统计量、P值则没有改变,与以实际人口规模计算结果完全相同。见表 2。
讨论CAT检验广泛应用于流行病学和遗传学领域,国内外已有很多学者用于检验基于基因型有关的病例对照研究[4-6],疾病发病率或死亡率等的时间趋势研究[7-8]。王立芹等[9]的研究显示,趋势χ2检验一般在有序R×C表的分析时使用,适用范围包括3类:① 分组变量有序,指标变量为二分类,例如研究多个百分率是否随着有序变量的不同存在线性变化趋势;② 分组变量无序,指标变量有序,例如研究不同药物(不同疗效)有无差别;③ 分组变量和指标变量都有序,例如研究两个有序的变量之间是否存在线性趋势。
线性回归一般用于描述随着时间的推移发生率的趋势的资料,前提是假定相邻两年疾病的率是稳定变化的[10]。国内外在研究疾病率的趋势分析已广泛使用APC等相关指标进行描述,比如巴西的骨髓白血病死亡率时间趋势分析[11],中国沈阳市新生儿死因死亡率的时间趋势分析[12],美国加州早期肝细胞癌诊断率的时间趋势分析[13]。
本研究通过实例分析发现,因人口基数的差异,CAT检验的结果与线性回归估计结果存在差异,即不同的趋势分析方法得出的结论可能不同,这在很多率的流行病学趋势研究中是经常遇到的。
探讨其原因,两种统计学方法的原理不同,由CAT检验计算统计量的公式可以看出,统计量的计算充分利用了R×2表格中的数据,即其统计量大小除了与分析年份多少有关外,还与人口数和发病人数密切相关,CAT检验P值变动较大,提示该方法对人口基数很敏感,人口基数多少是其检验效能大小的重要来源。而线性回归则是通过配合线性模型来实现,线性模型的自变量和应变量分别是年份和发病率的自然对数,再利用线性模型的回归系数 β的P值来估计线性趋势是否具有统计学意义,由公式及本研究结果可知,其统计效能与率值的点数即分析年份的多少密切相关,而与率值的分子分母,即人口数和发病人数无关。这种统计量之间的差异可能与人口数的变化、分析年份的多少有关。另外,我们统计的发病率总体上虽然是随着年份的增加有递增的趋势,但是从每年的数据来看不是完全的增长,中间年份的发病率有低于相邻年份的,由于其线性模型原理,模型有可能与样本的拟合度不好,损害了分析结果[14]。
但是,线性回归可以得出率的时间趋势指标APC,较直观地看出率的变化程度,利用线性回归做率的趋势变化分析时,不同资料之间的率可以比较其变化趋势的差异。并且线性回归不仅适用于计数(频率)资料的趋势分析,也适用于计量资料的趋势分析。虽然线性回归模型为参数模型,对资料要求较严格,但其又有丰富的衍生模型,包括多元线性回归、分类资料的回归、非线性回归等,其适用资料范围越来越广泛,特别是多元线性回归可以对可能的混杂因素进行控制,从而得出更科学的结论。CAT检验利用信息完全,但缺点是没有率的趋势指标,只适用于计数资料的趋势分析,并且其统计量与人口基数有关,不同资料(不同人口基数)之间率无法比较趋势的大小,在资料可能存在较多混杂因素时,不能通过多元分析进行混杂因素控制,只能采用分层方法。例如有学者认为,在研究不同组疾病的发生率时,CAT检验直接比较不同组的发生率而没有考虑不同组死亡率的差异,得出的结论可能存在偏倚,遂提出了Poly-k趋势检验[15]。
综上所述,在流行病学研究中,CAT检验和线性回归都已是成熟的统计分析方法。在满足基本适用条件的前提下,当人口数较大,有序分类变量(年份)较少时,宜选用CAT检验;当人口数较小,有序分类变量(年份)较多时,宜选用线性回归分析,这样更能充分发挥各自的统计效能优势,进而发现趋势性。同时也可以将两种方法相结合,发挥各自的优势,弥补各自的不足。希望研究者可以根据资料类型选择适宜的方法,以得出可靠的结论。
利益冲突: 无
| [1] |
胡良平, 郭辰仪, 李崇.
用SAS软件实现列联表资料趋势检验[J]. 药学服务与研究, 2013, 13(3): 174–176.
Hu LP, Guo CY, Li C. Statistical analysis and SAS solutions for contingency table applying trend test[J]. Pharm Care Res, 2013, 13(3): 174–176. DOI:10.5428/pcar20130305 |
| [2] | Khazaei S, Soheilyzad M, Molaeipoor L, et al. Trend of Smear-positive Pulmonary Tuberculosis in Iran during 1995-2012:a segmented regression model[J]. Int J Prev Med, 2016, 7: 86. DOI:10.4103/2008-7802.184317 |
| [3] |
项永兵, 张薇, 高立峰, 等.
恶性肿瘤发病率的时间趋势分析方法[J]. 中华流行病学杂志, 2004, 25(2): 173–177.
Xiang YB, Zhang W, Gao LF, et al. Methods for time trend analysis of cancer incidence rates[J]. Chin J Epidemiol, 2004, 25(2): 173–177. DOI:10.3760/j.issn.0254-6450.2004.02.022 |
| [4] | Lee WC. Optimal trend tests for genetic association studies of heterogeneous diseases[J]. Sci Rep, 2016, 6(1): 27821. DOI:10.1038/srep27821 |
| [5] | Wellek S, Ziegler A. Cochran-Armitage test versus logistic regression in the analysis of genetic association studies[J]. Hum Hered, 2012, 73(1): 14–17. DOI:10.1159/000334085 |
| [6] | Ahn K, Haynes C, Kim W, et al. The effects of SNP genotyping errors on the power of the Cochran-Armitage linear trend test for case/control association studies[J]. Ann Hum Genet, 2007, 71(Pt 2): 249–261. DOI:10.1111/j.1469-1809.2006.00318.x |
| [7] | Mirzaei M, Ghoncheh M, Pournamdar Z, et al. Incidence and trend of liver cancer in Iran[J]. J Coll Physicians Surg Pak, 2016, 26(4): 306–309. |
| [8] | Mirzaei M, Hosseini SA, Ghoncheh M, et al. Epidemiology and trend of head and neck cancers in Iran[J]. Glob J Health Sci, 2016, 8(1): 189–193. DOI:10.5539/gjhs.v8n1p189 |
| [9] |
王立芹, 刘殿武, 唐龙妹, 等.
有序R×2表资料线性趋势卡方检验与秩相关分析的比较[J]. 临床荟萃, 2009, 24(4): Ⅳ.
Wang LQ, Liu DW, Tang LM, et al. A comparative study on Cochran-Armitage trend method and Rank correlation method for the R×2 ordered table data[J]. Clin Focus, 2009, 24(4): Ⅳ. |
| [10] | Kazemnejad A, Arsang JS, Amani F, et al. Global epidemic trend of tuberculosis during 1990-2010:using segmented regression model[J]. J Res Health Sci, 2014, 14(2): 115–121. |
| [11] | Martins-Melo FR, Pinheiro MCC, Ramos AN Jr, et al. Trends in schistosomiasis-related mortality in Brazil, 2000-2011[J]. Int J Parasitol, 2014, 44(14): 1055–1062. DOI:10.1016/j.ijpara.2014.07.009 |
| [12] | Wu QJ, Li LL, Li J, et al. Time trends of neonatal mortality by causes of death in Shenyang, 1997-2014[J]. Oncotarget, 2016, 7(13): 16610–16618. DOI:10.18632/oncotarget.7670 |
| [13] | Rodriguez DN, Torruellas C, Cress RD. Trends in early-stage hepatocellular carcinoma, California 1988-2010[J]. Cancer Causes Control, 2016, 27(3): 325–331. DOI:10.1007/s10552-015-0705-2 |
| [14] |
陈勇, 陈建国, 沈洪兵, 等.
启东1972-2001年恶性肿瘤发病率时间趋势分析[J]. 疾病控制杂志, 2006, 10(2): 105–108.
Chen Y, Chen JG, Shen HB, et al. Time trend analysis on incidence rate of malignant tumor in Qidong, 1972-2001[J]. Chin J Dis Control Prev, 2006, 10(2): 105–108. DOI:10.3969/j.issn.1674-3679.2006.02.001 |
| [15] |
柳伟伟, 胡良平, 高月, 等.
Poly-k趋势检验在啮齿类动物致癌性实验中的应用[J]. 军事医学, 2013, 37(7): 521–524.
Liu WW, Hu LP, Gao Y, et al. Application of Poly-k trend test in rodent carcinogenicity experiments[J]. Mil Med Sci, 2013, 37(7): 521–524. DOI:10.7644/j.issn.1674-9960.2013.07.011 |
 2017, Vol. 38
2017, Vol. 38