1. 730000 兰州大学公共卫生学院流行病与卫生统计研究所;
2. 730000 兰州大学信息与工程学院计算机软件与理论研究所
收稿日期: 2016-09-08
基金项目: 教育部人文社科基金（15XJC910001）；兰州大学中央高校基本科研业务费（lzujbky-2016-025）
Evaluation of estimation of prevalence ratio using bayesian log-binomial regression model
1. Department of Epidemiology and Health Statistics, School of Public Health, Lanzhou University, Lanzhou 730000, China;
2. Department of Computer Software, School of Information and Engineering, Lanzhou University, Lanzhou, 730000, China
Fund program: Humanities and Social Sciences Foundation of the Ministry of Education of China (15XJC910001); Fundamental Research Funds for the Universities Subordinated to Central Government of China (lzujbky-2016-025)
在横断面研究中，log-binomial回归能够获得因素与结局变量的关联强度指标患病率比（prevalence ratio，PR），是一种研究二分类观察结果与多因素之间关系的重要方法，在医学研究等领域中得到了广泛的应用[1-3]。贝叶斯log-binomial回归是将log-binomial回归估计的回归参数和结局变量看成是具有某个特定分布的随机变量，在事先指定其先验分布的前提下，利用贝叶斯公式，获得它们的后验分布或概率，从而达到参数估计[4-5]。与常规的log-binomial回归相比，贝叶斯log-binomial回归引入了随机变量，在处理不确定性或随机问题时，表现出明显的优势。此外，处理问题的灵活性也得到了很大的增强。本文主要介绍贝叶斯log-binomial回归PR估计的方法，并用看护人识别腹泻危险症状与婴幼儿腹泻求医关系的实例来验证模型估计PR的可行性和有效性。
基本原理
log-binomial回归模型：
在log-binomial回归模型中，观察的结局变量Y（Y＝1，出现阳性结果；Y＝0，出现阴性结果）为两分类变量，服从二项分布，且结局变量Y＝1的概率P的对数值与自变量X呈线性关系：
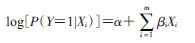(1)
在式（1）中，log（·）是以自然数e为底的对数函数，α为截距，βi（i＝1，2，…，m）分别为自变量Xi（i＝1，2，…，m）的回归系数。由于P（Yi＝1|Xi）的取值界于0和1之间，所以log[P（Y＝1|Xi）]取值位于（-∞，0）区间内。在用最大似然估计方法进行参数估计时，需要保证限定条件
成立的情况下才能进行。当模型中存在连续自变量时，最大似然估计的参数落在该限定条件的边界上，而得不到最大似然函数导数为零时的解，从而使模型不能收敛。
Deggens等[6]提出了扩充原始数据集，在扩充的数据集上运行log-binomial回归模型能够获得最大似然的近似估计值。扩充原始数据集的步骤：当log-binomial回归模型不收敛时，将原始数据集中Y＝1的个案增加c-1倍，然后，再将原始数据集中Y值互换，将这两个新的数据集合并成一个数据集，即为复制（COPY）数据集。再利用COPY数据集拟合log-binomial回归模型从而达到解决模型不收敛问题。通常c为常数，c越大，COPY数据集的伪似然估计值越接近于最大似然估计值。在SAS软件中，可以利用genmod模块中的加权log-binomial回归模型实现COPY数据集下的log-binomial回归方法[7]。
贝叶斯log-binomial回归模型：
利用贝叶斯方法实现log-binomial回归参数估计，需要将模型中各估计参数看成是随机变量，指定其先验分布，然后，结合样本信息计算其后验分布，以实现模型参数的估计。由式（1）可见，log-binomial回归通过对数连接（通常取自然数e为底的对数），将每个观测Y＝1的概率Pj（j＝1，2，…，n）的对数与线性部分连接。如式（2）所示：
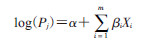(2)
在式（2）中，估计的参数为回归系数βi（i＝1，2，…，m）。截距α和回归系数βi（i＝1，2，…，m）在[-∞，∞]取值。通常不合适的先验会对后验估计结果产生影响，因此，按照截距和回归系数的测量尺度，设定为建议的正态分布先验，考虑到指定的先验分布精度对参数后验分布的影响，可采用很小精度的无信息先验分布，如式（3）和（4）所示。用N（μ，τ）表示以均数μ和精度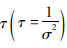
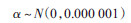为参数的正态分布。
(3)
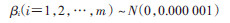(4)
在式（2）中，Pj（j＝1，2，…，n）为每一观测结局变量Y＝1的概率，取值界于0和1之间。而每一个观测的结局变量值Yj（j＝1，2，…，n）可以看成是以概率Pj进行的一次贝努利抽样的结果。此时，模型可以指定如下先验式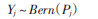（5）：
(5)
式（5）中Bern（Pj）为以概率Pj为参数的贝努利分布概率密度函数。
直接利用贝叶斯公式进行log-binomial回归模型参数求解，涉及到非常复杂的多重积分形式。此时，可以将参数求解的过程看成是一条或多条马尔可夫链（可以指定不同的初始值来确定），利用蒙特卡罗模拟和Gibbs抽样方法实现。
设存在样本量为n的横断面样本，二元结局变量Y，有m个自变量分别为Xi（i＝1，2，…，m）。利用贝叶斯log-binomial回归模型估计自变量的PR用于测量它与结局变量间的联系。在Openbugs软件中，可以通过基本程序来实现，见程序1。
程序1：
在贝叶斯log-binomial回归中，参数估计需要满足限定条件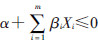
。当存在连续自变量时，可能会导致模型不收敛。Chu和Cole[8]在后验概率估计公式中增加了不平等限制改善不收敛问题。在程序中需对每一步中观测的后验概率进行不等式约束，见程序2。
程序2：
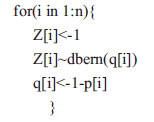
在Openbugs中模型运行时，为了监视模型的收敛，需要设定多条不同初始值链，收敛情况可以通过轨迹图、BGR图直观地监测；为了保证样本是从后验分布中抽取，通常设定退火参数burn-in；各链的自相关程度可以通过自相关图观测，为了有效降低抽样过程中链间的自相关程度，可以根据不同马尔可夫链自相关程度设置thin参数值；为了减低蒙特卡罗误差，需要更多的额外抽样用于参数估计[9]。
实例分析
实例采用西安交通大学2005年西部农村10个省份（甘肃、广西、贵州、江西、内蒙古、宁夏、青海、四川、新疆和重庆）妇幼卫生调查数据库中，婴幼儿腹泻求医行为相关数据作为基础数据。利用贝叶斯log-binomial回归探索看护人识别腹泻危险症状与婴幼儿腹泻求医率之间的关系。调查数据库中共包含了10个省份的14 112名婴幼儿及家庭信息，1 040名婴幼儿在调查前2周内患有腹泻，婴幼儿2周腹泻患病率为7.4%。在1 040名腹泻患儿中，795名腹泻患儿在医疗机构就诊，2周腹泻求医率为76.40%；看护人识别腹泻危险症状的比例为29.23%。研究中所调整协变量的基本信息见表 1。由于2周腹泻求医率远高于10.00%，因此，需要用PR来评估因素与结局变量之间的关系，log-binomial回归可直接获得各因素与结局变量间的PR值。
采用贝叶斯log-binomial回归从3个模型分析看护人识别腹泻危险症状与婴幼儿腹泻求医之间的关系。模型1：未调整协变量；模型2：调整看护人受教育的年限；模型3：在模型2基础上，调整村乡间的距离和患儿月龄。模型的拟合优度通过偏差信息统计量（deviation information criteria，DIC）分析最优模型。为了更好地比较，同时也拟合了3个常规log-binomial回归模型，当模型不收敛时，采用COPY方法进行参数估计。贝叶斯log-binomial回归采用Openbugs软件（http://www.openbugs.net）进行统计分析，常规log-binomial回归和加权log-binomial回归（实现COPY方法）采用SAS 9.1.2软件（SAS Institute Inc.，Cary，North Carolina）进行统计分析。
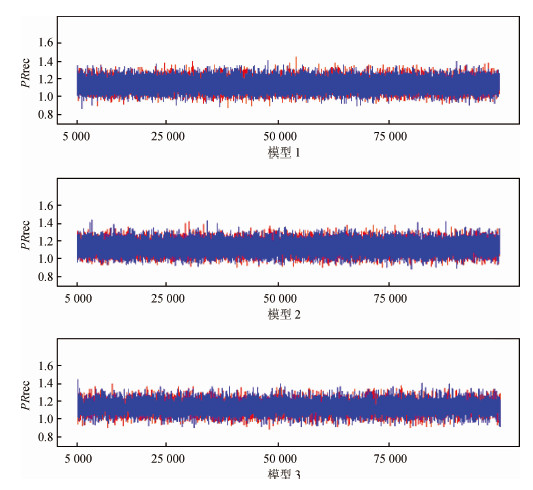
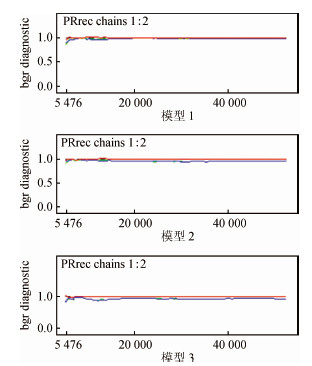
在贝叶斯log-binomial回归参数估计过程中，为了监视模型的收敛情况，根据模型的约束条件和回归系数的取值范围（回归系数初始值分别设置在-1和0）运行不同初始值的2条链，收敛情况直观地通过迭代轨迹图来分析。通过抽样更新，每100次迭代更新1次，每10次更新通过迭代轨迹图、历史轨迹图以及BGR图观察各链收敛情况，发现5 000次迭代后，各链趋于收敛。为了确保从后验分布中抽样且参数的估计值不会受到初始值的影响，在参数估计时，通过设定退火参数burn-in，将前期5 000次的迭代结果剔除。为了减少蒙特卡罗误差，额外的100 000次抽样用来估计后验参数。为了更好地降低链间的自相关，贝叶斯模型的参数thin设定为5。在3个贝叶斯log-binomial回归模型运行后，各估计参数的蒙特卡罗误差均＜5%标准差；自相关指标提示各链混合较好。3个贝叶斯log-binomial回归模型中，看护人识别危险症状变量的历史轨迹图、BGR图和自相关图分别见图 1~3。此外，3个模型中，模型3运行时间稍长于其他2个模型，运行时间也在可接受的范围内。3个贝叶斯log-binomial回归模型拟合优度参数的比较，模型1的DIC最小（DIC＝1 763），因此，模型1是最优模型。
拟合常规log-binomial回归模型，模型1和模型2均能收敛，但模型3不收敛，采用COPY方法进行参数估计，而3个贝叶斯log-binomial回归模型均能收敛；比较看护人识别腹泻危险症状与求医关系的PR的点估计值，贝叶斯log-binomial回归模型2和模型3均较常规log-binomial回归稍大，模型1两者相等；区间估计贝叶斯log-binomial回归较常规log-binomial回归稍宽。不同模型估计的看护人识别腹泻危险症状与求医关系的PR结果见表 2。贝叶斯log-binomial回归结果显示，看护人识别腹泻危险症状可提高13%的婴幼儿腹泻求医的概率（贝叶斯最优模型结果）。
表 2 贝叶斯log-binomial回归与常规log-binomial回归结果
讨论
在流行病学横断面研究中，当疾病的流行水平较高（＞10%），OR值会高估因素与疾病间的联系。Lee和Chia[10]建议使用PR值来估计因素与结局变量间的关系。log-binomial回归作为一种直接获得PR的指数风险模型，已被研究者广泛关注。但是，log-binomial模型中，当出现连续自变量时，有时会出现模型不收敛的问题[6]。尽管Deggens提出了扩充原始数据集，然后运行log-binomial回归模型能够获得最大伪似然估计值，Savu等[11]也证明了这个最大似然估计值是存在的，且是唯一的，但是这种方法调整了数据集本身的结构，有点特别且缺乏一般性[6, 8]。
本研究运用贝叶斯log-binomial回归估计PR，用实例分析看护人识别危险症状与婴幼儿腹泻求医之间的关系，并同常规log-binomial回归结果进行了比较。结果显示，看护人识别腹泻危险症状可提高13%的婴幼儿腹泻求医的概率。各模型的比较结果表明，贝叶斯log-binomial回归与常规log-binomial回归估计的看护人识别腹泻危险症状与求医关系PR的点估计和区间估计，在不同模型中虽有微小差别，但整体估计的一致性较好，说明贝叶斯log-binomial回归在无协变量、有协变量情形下，估计变量的PR是有效的。此外，贝叶斯log-binomial回归应用中，无论有无连续协变量，通过增加对每一步观测的后验概率进行不等式约束程序，监视概率变化，避免了概率越界或边界概率导致模型不收敛的问题。
有研究表明，可选择使用其他的替代模型来估计因素的PR，但这些模型常出现模型拟合有关的问题。Zou[12]利用Poisson回归估计PR，但Poisson误差通常较二项误差大，还常会出现概率越界问题[8, 13-14]。Lee和Chia[10]推荐设定一个不变的随访时间，使用Cox风险回归估计因素的PR，但患病率很高时，会产生更大的标准误[15]。此外，一些研究直接利用logistic回归估计PR。Zhang等[16]将logistic回归估计的OR值，通过OR和PR的转化公式，简单地获得PR值的点估计和区间估计，但有混杂因素时这个方法会产生较大偏倚。Schouten等[17]通过一定规则扩充数据集后使用logistic回归来获得PR的估计，但该方法需通过调整原始数据集，估计过程有点繁琐。
由于贝叶斯log-binomial回归使用了MCMC模拟的方法进行参数估计，这种模拟方法对每一观测后验概率进行不等式约束后不会依赖非对称近似，当样本量很小的时候，依然能得到概率的区间估计[8]。另外，对后验概率的不等式约束，降低了模型不收敛而导致无法参数估计的风险，与常规的log-binomial回归相比，使估计参数的问题更加直接，无需转换方法来完成PR的估计。
总之，在横断面研究中，当疾病的流行水平较高时，贝叶斯log-binomial回归方法能够较好地估计各因素的PR，由于对后验概率不等式约束，很少出现模型不收敛导致的无法估计参数的问题，较常规的log-binomial回归在估计PR上更有优势。
利益冲突:
无
2017, Vol. 38
表1(Table 1)
