文章信息
- 范伟, 沈超, 郭志荣.
- Fan Wei, Shen Chao, Guo Zhirong.
- 基于模型的多因子降维方法在基因-基因/环境交互作用分析中的应用
- Detecting gene-gene/environment interactions by model-based multifactor dimensionality reduction
- 中华流行病学杂志, 2015, 36(11): 1305-1310
- Chinese Journal of Epidemiology, 2015, 36(11): 1305-1310
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2015.11.024
-
文章历史
- 投稿日期: 2015-03-17
目前研究表明包括癌症、心血管病等在内的多数复杂疾病,同时受到多个遗传及环境因素的影响,因此研究基因和环境因子在复杂疾病发展中的效应已成为遗传流行病学研究的一个重要方向。随着受关注的与疾病相关因子数目不断增加,在多因子交互分析中传统的logistic回归方法受到极大限制[1],而多因子降维法(MDR)可实现分析基因-基因/环境交互作用的目的,并在多项研究中得到应用[2]。但该法存在局限性,随后有学者又提出了广义多因子降维法(GMDR)[3]作为经典MDR方法的扩展,但GMDR的原理很大程度上与MDR并无明显差异。两法在合并单元格(即因子不同观察水平的组合)时,仅通过与总体的病例对照比值(MDR)或某一特定预设阈值比较来评估风险,而未做相应的统计推断,因此当同一风险类别中合并了过多的单元格时,往往忽略或误判某些重要的交互作用,在实际应用时造成统计效能的降低[4]。为此,本文介绍另一种MDR的扩展方法——基于模型的MDR方法(model-base multifactor dimensionality reduction,MB-MDR)[4],以解决许多MDR的不足,适用于数量性状以及二元性状对混杂因子调整,也能大大提高MDR及其他MDR扩展方法的统计效能。
基本原理MB-MDR同样是对原始MDR的一种扩展。但MB-MDR并不将原始数据集分为训练样本和验证样本,而是基于全部的原始数据。在降维过程中,仅有显著危险的观察水平组合才合并为高危(H)或者低危(L)类别,而不存在显著关联或者不具备足够样本数量的组合则被归为无风险(0)类别。其原理如图 1所示。
 |
| 图 1 MB-MDR基本步骤 |
1. 基本步骤[4]:以Cj(j∈N+)表示两因子特定观察水平的组合(即图 1中的单元格),N表示所有观察水平的组合总数。
(1) 第一步: 根据关联检验结果,将各两因子观察水平的组合(即基因型组合或者基因型-环境组合)Cj,归为H、L以及0中的一个类别。关联检验即判定该特定因子水平的组合是否与选择的表型存在统计学关联,该检验可以是非参数检验(χ2检验)或者参数检验(如logistic回归),而参数检验可以进行因子主效应(边际效应)或者混杂效应的调整。假设ORj=1[即回归系数βj=0,βj=ln(ORj)],其中ORj表示暴露相应组合Cj的个体与其余非暴露该组合个体的OR值。
对两因子某种水平的组合与表型的关联检验采用的检验水准为α=0.10,以获得较高的统计检验效能。当ORj>1且P<0.10时,组合Cj被归为H类别;当ORj<1且P<0.10时,组合Cj被归为L类别;而P>0.10的组合Cj则被归为0类别。如选择的表型为数量性状[5],则进行t检验,比较该组合的均值与其余8个组合(单元格)的均值。t值的正负则代表相应的类别,t值为正,则Cj被归为高危类别;t值为负,则Cj被归为低危类别。
第一步的结果将返回一个新的分类变量X,包括H、L和0类别。此外,nH、nL分别代表H和L类别中合并的单元格数目,该两值将用以第三步置换检验评估。
(2) 第二步:主要进行有关新分类变量X(H,L,0)和结局变量Y的关联检验。与第一步进行的关联检验相同,此时可以是非参检验(χ2检验)亦或是参数检验(如logistic回归),而后者可以进行相应的协变量调整。ORH和ORL分别代表H、L风险类别的OR值,其中ORH为在高风险类别中的人群与剩余个体的OR值,ORL则为在低风险类别中个体数与剩余个体数的OR值。对应的回归系数以bH和bL表示,其中βH=ln(ORH),βL=ln(ORL)。
(3) 第三步:回归系数的统计学分析仍采用Wald统计量判定,即W=[β/se(β)]2=T2。通过第一步的单元格合并后,该统计量不再服从χ2/t分布,W/T值变大,而通过原始χ2/t分布的原始P值则变小,因此不宜采用原始P值。此时需调整每个类别中的合并组合数目(nH和nL)。此时,运用置换检验方法,求出合并单元格后W统计量的原始置换分布(permutation null distribution,Wjk)即合并单元格数为k,模型的阶数为j时的条件分布,得出调整后的P值。
2. 软件分析处理:MB-MDR计算处理主要采用R软件(3.2.0)的mbmdr2.6程序,并可在CRAN(The Comprehensive R Archive Network)网站下载。
3. MB-MDR分析的数据格式:同一般的数据库记录的格式相同,用于计算数据集的每一列(attributes)代表一个变量,即研究的各个因子(遗传、环境因素以及表型等),数据集的每一行(instances)则表示一个记录,即代表相应的个体(individuals)。通常1个单核苷酸基因多态性(SNP)具有2种不同的等位基因(一般等位基因和次要等位基因),分别以A和a表示,用于MB-MDR的数据集中以0代表野生纯合子(AA),1代表杂合子(Aa),2代表突变纯合子(aa)。除了各SNP的基因型以外,数据集中还应当包括因变量Y(通常为所选择的表型,可以是分类变量,也可以是连续型的变量),以及其他用于分析调整的混杂因素Ci(i=1,2,…,N)。
4. 程序的编写与运行:首先建立相应的R程序工作空间,然后安装、加载mbmdr程序软件、导入数据集,具体操作可参考相关文献。MB-MDR程序软件主要包含2个运算函数(过程),即mbmdr以及mbmdr.PermTest。各功能及应用方式简述如下[更多详细说明可输入“help(package=mbmdr)”语句查看]。
(1) mbmdr函数:可求得MB-MDR计算过程中第一和第二步的结果。mbmdr函数格式:mbmdr(y,data,order,covar=NULL,exclude=NA,risk.threshold=0.1,output=NULL,adjust=c(“none”,“covariates”,“main effects”,“both”),first.model=NULL,list.models=NULL,use.logistf=TRUE,printStep1=False,…)。式中各参数分别表示:① y为因变量;②data为所要分析的数据集名称;③order为用于指定所要分析的交互作用的具体阶数,默认列出所有各阶模型的结果;④covar为指定所要调整协变量;⑤ exclude定义为缺失值在数据集中的具体值;⑥risk.threshold为指定第一步中采用的检验水准,默认为0.10;⑦ output为指定结果的输出形式;⑧adjust为回归的调整类型,有4个可选项,默认为“none”,即不调整;⑨first.model为用于指定所要分析的首个交互因子的组合,默认所有的因子模型组合都会被纳入进行分析;⑩ list.models为指定满足特定条件的模型的清单;use.logistf为当因变量为离散时,指定是否调用logistf软件进行logistic回归的运算;printStep1为指定是否输出第一步中各因子组合对于结局的关联结果。
另外,还需要用户根据结局类型指定误差分布和关联函数的类型。如family=binomial(link=“logit”)用于logistic回归;family=gaussian(link=“identity”)用于一般线性回归分析(用于数量性状)。
(2) mbmdr.Permtest函数:该函数用于对由mbmdr函数计算得到的交互模型结果进行置换检验。格式为:mbmdr.Permtest(x,n,model=NULL,sig.level=1)。式中,各参数分别表示:① x表示通过mbmdr函数过程所返回的mbmdr对象;② n为置换的次数;③model为指定需要进行置换检验的交互模型,默认model=NULL,表示只显示x对象中最佳模型(adjusted P值最小)的置换检验结果;④ sig.level为指定计算置换检验P值的置信区间所采用的显著性水平(正态近似法)。最终该函数结果中将会给出max(WH,WL)及由置换检验得出的调整P值(adjusted P;即软件结果给出的Perm P)。
实例分析本文以“江苏省多代谢异常和代谢综合征综合防治研究(PMMJS)”中基线获得的遗传学相关数据为基础进行横断面分析。由于过氧化物酶体增殖物激活受体(PPAR)可通过多种途径影响血清LDL-C水平[6, 7],研究中采集江苏省常熟市820名研究对象的基线血标本检测PPAR基因多态性,共测定3个PPAR基因(PPARα/δ/γ)的10个SNP位点[8]:PPARα基因(rs135539,rs1800206,rs4253778)、PPARδ基因(rs2016520,rs9794)以及PPARγ基因(rs709158,rs10865710,rs1805192,rs4684847,rs3856806),以二元表型纳入模型进行分析,探索PPAR基因的10个位点是否存在对体内LDL-C水平的交互作用。其中LDL-C水平≥4.14 mmol/L定义为高LDL-C血症[9],<4.14 mmol/L为对照。调整饮酒、BMI及腰围后,共有4个位点与高LDL-C血症存在阳性关联(α=0.005,共显性模型): rs1800206(P<0.000 1)、rs9794(P=0.000 7)、rs1805192(P<0.000 1)和rs3856806(P=0.002)。
以3阶交互作用为例,介绍MB-MDR的运行原理。
首先,MB-MDR计算所有3因子(即3个SNP)不同观察水平组合的风险,由于共纳入10个SNP,因此因子的组合总数共有C103=120种;而每个SNP(遗传因子)有3种不同的基因型,因此每3个因子的观察水平组合共有33=27种。由于组合数目较多,仅以其中某一组合为例,分别介绍MB-MDR各步骤的计算过程。
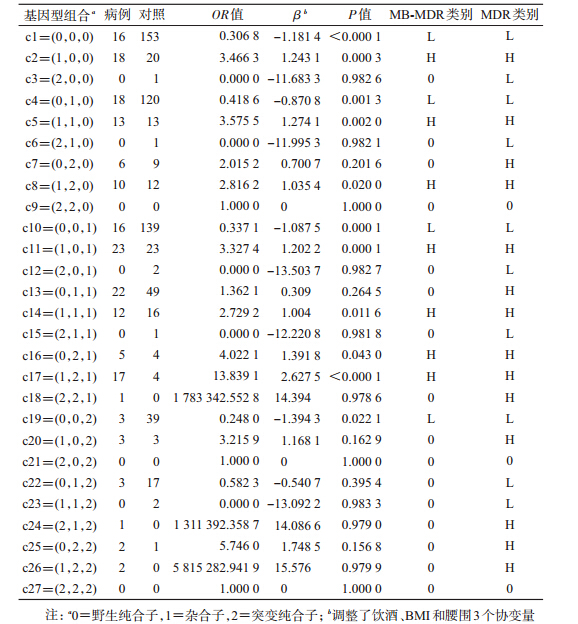
1. 第一步: 以MDR识别为最佳模型的3个SNP(rs1800206、rs1805192和rs709158)的交互作用为例,利用MB-MDR分析这3个位点不同基因型组合与高LDL-C血症的关联。采用logistic回归分析调整饮酒、BMI和腰围3个变量,比较某一特定基因型的个体与其余不含有该基因型个体的风险,根据OR值判断两位点的基因型组合属于H还是L类别。由于每个位点具有3种不同的基因型,因此共进行27个logistic回归。如表 1所示,基因型组合c1、c4、c10和c19的OR<1且P<0.10,因此被归类为L类别组;而基因型组合c2、c5、c8、c11、c14、c16和c17的OR>1且P<0.10,因此被归类为H类别组;其余P>0.10基因型组合则被归为0类别组。
2. 第二步:继续分析同一风险类别中基因型组合合并后,相应的风险类别(H或L)与高LDL-C血症的关联,即合并基因型组合c1、c4等4个L类别以及c2、c5等7个H类别。其中运用2个logistic回归,同样调整了饮酒、BMI和腰围3个混杂变量:第一个模型比较L组中个体与其余个体(非L组)的风险,而第二个比较H组中的个体与其余个体(非H组)的风险,结果如表 2。
3. 第三步:通过对L、H类别中较大的Wald值(Wmax)进行置换检验,从而进一步确定特定的3阶模型交互模型中,H/L(Wmax)类别对于表型关联结果的统计学显著性,以判定该交互作用模型存在与否。最终在0.05水平下采用控制错误发现率(false discovery rate,FDR)方法进行多重检验之后,共有91个3阶模型显示对高LDL-C血症存在显著的基因-基因交互作用(表 3)。此外还发现,rs1805192、rs4253778和rs1800206组合为最佳模型,即调整P 值(adjusted P)最小,并且除了MDR识别到的交互组合(rs709158、rs1805192和rs1800206)之外,还有其他多个3阶(位点)交互作用也具有显著性,表明这些3阶模型都存在对于高LDL-C血症的基因-基因交互作用,而这些很可能在采用MDR时被忽视和遗漏。同时,研究者也可根据实际研究问题的需要,在指定阶数条件下,只对最佳交互作用模型(或指定的交互作用模型)进行统计学判定,从而提高研究特定问题的效率。
近年来,遗传分子技术的不断普及和改善使得快速、高效的遗传位点的基因分型成为可能。越来越多的研究者开始关注多个遗传因素和环境因素对于某些复杂疾病的作用。但是由于样本量、伦理以及研究成本等诸多原因,在人群中基因-基因/环境交互作用的研究依然主要依靠相应的统计工具。虽然传统的logistic回归分析方法可通过在模型中加入相乘项的方式用于分析2个或3个因子的交互作用对结局(表型)的影响,但是当分析多个因子(特别是>4个时),使用该种方法往往需要过多的自由度或者样本量,强制使用常常会因为某些分类中个案的缺失造成模型系数无法收敛,因此,当样本量不是很大时,常常难以用于多因子交互的分析和评价。MDR是近年来提出的一种非参数、无需遗传模式的分析方法,是以疾病易感性分类的方式建模,为处理高维数据理想的方法[10]。
作为经典MDR的扩展,MB-MDR弥补了MDR的不足,其中包括[4]:①当病例对照人数比值与所有样本人群的病例对照人数接近或者样本较小时,由于未进行相应的统计推断,易导致假阳性或者假阴性分类;②无法调整混杂因子;③不能分析数量性状;④无法调整因子的边际效应(marginal effect); ⑤当模型中存在拟表型(phenocopies)和遗传异质性(genetic heterogeneity)等噪声时,统计效能(power)有限[11];⑥计算量大。基于经典MDR的局限性,Lou等[3]提出了GMDR,而MB-MDR与GMDR的区别主要在于2个方面,首先对风险单元格的定义不同;其次,选择最佳模型的方法策略不同。MB- MDR通过对单元格(即不同因子观察水平的组合Cj)与所选表型的关联检验的假设检验获得对风险单元格的评估。是将关联检验的P值(可能调整了混杂因素)与预先设定的阈值(程序默认为0.10)相比从而得到一个多因子水平(H、L、0类别)的一维结构,而GMDR并不通过计分或者似然特征对风险单元格进行评估,而是将每万单元格内个体的计分均值(可能调整了混杂因子)与预先指定的阈值(如0)进行比较,从而产生一个新的(2个)风险组的结果[12];此外,MB-MDR并不将数据集分为训练集和验证集,因此也不通过预测精度和交叉验证方法来选择最佳的交互模型,这也是与其他MDR扩展方法的最大的不同之处。由于MB-MDR在分析过程中进行了大量的假设检验,因此当纳入分析的因子数目过多时,如果仍然按照个体的检验水准α=0.05,则可能出现假阳性结论的个数增多。此时,进行多重检验就显得尤为必要。生物医学数据中,针对多重检验情况较为常用的方法主要有控制总Ⅰ型错误率(FWER)和控制FDR[13],其中当涉及的假设检验数较多时尤以后者更为合适[14]。
总之,MB-MDR作为原始MDR的扩展,可应用于多因子交互作用的探索、识别和检验,在研究基因-基因/环境交互作用方面具有良好的应用前景。该法既可用于二元性状,亦可用于数量性状[15],并通过增加统计推断的方法,大大提高了多因子交互作用模型识别的把握度及可靠性。不过,当模型中存在拟表型和遗传异质性等噪声时,MB-MDR统计效能依然有待提高;由于该法未采用并行计算,在大规模的基因组数据的实际应用中仍受到计算机计算量和内存容量的限制,因此还有待提高和优化。
| [1] Tang X,Li N,Hu YH. The application of multifactor dimensionality reduction for detecting gene-gene interactions[J]. Chin J Epidemiol,2006,27(5):437-441. (in Chinese) 唐迅,李娜,胡永华. 应用多因子降维法分析基因-基因交互作用[J]. 中华流行病学杂志,2006,27(5):437-441. |
| [2] Ritchie MD,Hahn LW,Roodi N,et al. Multifactor- dimensionality reduction reveals high-order interactions among estrogen-metabolism genes in sporadic breast cancer[J]. Am J Hum Genet,2001,69(1):138-147. |
| [3] Lou XY,Chen GB,Yan L,et al. A generalized combinatorial approach for detecting gene-by-gene and gene-by-environment interactions with application to nicotine dependence[J]. Am J Hum Genet,2007,80(6):1125-1137. |
| [4] Calle ML,Urrea V,Malats N,et al. MB-MDR:model-based multifactor dimensionality reduction for detecting interactions in high-dimensional genomic data[J]. Ann Hum Genet,2008,75:1-14. |
| [5] Mahachie John JM,van Lishout F,van Steen K. Model-Based Multifactor Dimensionality Reduction to detect epistasis for quantitative traits in the presence of error-free and noisy data[J]. Eur J Hum Genet,2011,19(6):696-703. |
| [6] Tanaka T,Ordovas JM,Delgado-Lista J,et al. Peroxisome proliferator-activated receptor alpha polymorphisms and postprandial lipemia in healthy men[J]. J Lipid Res,2007,48(6):1402-1408. |
| [7] Rudkowska I,Dewailly E,Hegele RA,et al. Gene-diet interactions on plasma lipid levels in the Inuit population[J]. Br J Nutr,2013,109(5):953-961. |
| [8] Luo WS,Guo ZR,Wu M,et al. Association of both peroxisome proliferator-activated receptor,gene-gene interactions and the body mass index[J]. Chin J Epidemiol,2012,33(7):740-745. (in Chinese) 骆文书,郭志荣,武鸣,等. 过氧化物酶体增殖物激活受体单核苷酸多态性以及基因-基因交互作用与体重异常的关系[J]. 中华流行病学杂志,2012,33(7):740-745. |
| [9] Zhu JR. Chinese guidelines on prevention and treatment of dyslipidemia in adults (no abstract)[J]. Chin J Cardiol,2007,35(5):390-419. (in Chinese) 诸俊仁. 中国成人血脂异常防治指南[J]. 中华心血管病杂志,2007,35(5):390-419. |
| [10] Hahn LW,Moore JH. Ideal discrimination of discrete clinical endpoints using multilocus genotypes[J]. In Silico Biol,2004,4(2):183-194. |
| [11] van Steen K,Cattaert T,Calle ML,et al. A detailed view on model-based multifactor dimensionality reduction for detecting gene-gene interactions in case-control data in the absence and presence of noise[J]. Genet Epidemiol,2010,34(8):933-934. |
| [12] Chen Q,Tang X,Hu YH. Detecting interaction for quantitative trait by generalized multifactor dimensionality reduction[J]. Chin J Epidemiol,2010,31(8):938-941. (in Chinese) 陈卿,唐迅,胡永华. 应用广义多因子降维法分析数量性状的交互作用[J]. 中华流行病学杂志,2010,31(8):938-941. |
| [13] Li W. Research on multiple testing with applications in biological data[D]. Jinan:Shandong University,2014. (in Chinese) 李伟. 多重检验相关研究及其在生物数据上的应用[D]. 济南:山东大学,2014. |
| [14] Benjamini Y,Hochberg Y. Controlling the false discovery rate-a practical and powerful approach to multiple testing[J]. J Roy Stat Soc Ser B-Methodol,1995,57(1):289-300. |
| [15] Mahachie John JM,Baurecht H,Rodríguez E,et al. Analysis of the high affinity IgE receptor genes reveals epistatic effects of FCER1A variants on eczema risk[J]. Allergy,2010,65(7):875-882. |
 2015, Vol. 36
2015, Vol. 36