文章信息
- 何斐, 肖仁栋, 俞婷婷, 张鑫, 刘志强, 蔡琳. 2015.
- He Fei, Xiao Rendong, Yu Tingting, Zhang Xin, Liu Zhiqiang, Cai Lin. 2015.
- 运用广义线性模型探讨福建省汉族人群原发性肺癌影响因素
- Explore the influence factors on primary lung cancer in Fujian province Han population under the use of generalized linear model
- 中华流行病学杂志, 2015, 36(8): 896-899
- Chinese Journal of Epidemiology, 2015, 36(8): 896-899
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2015.08.027
-
文章历史
- 投稿日期:2015-01-14
2. 350108 福州, 福建医科大学公共卫生学院附属第一医院胸外科
2. Department of Thoracic Surgery, the First Clinical Medical College, Fujian Medical University, Fuzhou 350108, China
目前流行病学数据分析的思路最常见的是先描述研究对象的基本特征,后进行单因素分析,再考虑分层分析,最后为多元回归分析[1]。现今对应变量为二分类或多分类而言,logistic回归分析是最常用的方法。但流行病学研究的疾病,特别是肿瘤等慢性病却是多因素多阶段作用的结果,病因极其复杂,个体行为及环境因素等多方共同作用关系尚不明确。所有因素之间的相互作用形式在分析前无法预知,但分析时却经常直接使用相乘模式探讨自变量间的关系,因而可能无法拟合出最优模型。为此本研究以福建省汉族人群原发性肺癌危险因素为例,探讨流行病病因学研究中数据分析的新思路。
基本原理针对暴露于发病相关因素的疾病发生率构建广义线性模型,即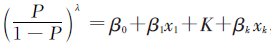 ,将其进行Box-Cox幂变换得到方程式[2]
,将其进行Box-Cox幂变换得到方程式[2]
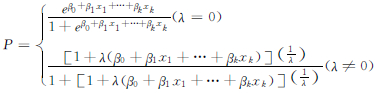
通过估计模型中的尺度参数λ大小判断各发病相关因素间的作用形式。λ=0时,判定因素间作用形式为相乘作用模型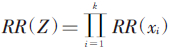 ;λ=1时,判定因素间作用形式为相加作用模型
;λ=1时,判定因素间作用形式为相加作用模型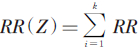 (xi)-(k-1);λ>1时,判定因素间作用形式为次相加作用模型
(xi)-(k-1);λ>1时,判定因素间作用形式为次相加作用模型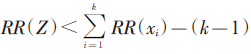 ;λ<0时,判定因素间作用形式为超相乘作用模型RR(Z)>
;λ<0时,判定因素间作用形式为超相乘作用模型RR(Z)>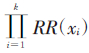 ;0<λ<1时,判定因素间作用形式为中间模型,即超相加或次相乘模型。
;0<λ<1时,判定因素间作用形式为中间模型,即超相加或次相乘模型。
运用广义线性模型建立2个连接函数 和
和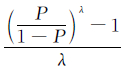 ,并计算模型拟合的偏差度(deviance)及模型的Pearson χ2值,通过改变λ的大小选择一系列偏差度中的最小值且同时经Pearson χ2拟合优度检验显示结果有统计学意义(P<0.05)此时对应λ值者即为选定的λ值。
,并计算模型拟合的偏差度(deviance)及模型的Pearson χ2值,通过改变λ的大小选择一系列偏差度中的最小值且同时经Pearson χ2拟合优度检验显示结果有统计学意义(P<0.05)此时对应λ值者即为选定的λ值。
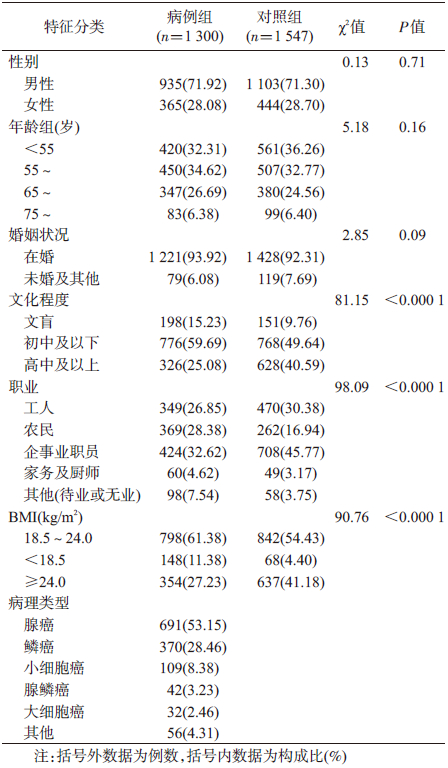
选取2006年1月至2013年1月福建医科大学附属第一医院、协和医院和南京军区福州总医院胸外科及呼吸内科确诊的1 300例新发原发性肺癌患者为病例组,同期选取1 547名到上述医院其他科室探视患者的亲友以及社区人群,在排除肿瘤病史后按相同性别、年龄(±2岁)频数匹配作为对照组。以调查表面访形式,调查一般情况(性别、年龄、婚姻状况、职业、文化程度及BMI)、室内外环境(居住地污染、房屋类型、住房通风、烹调燃料、烹调油烟、烹调用油热度、装修、吸烟、吸烟包年、戒烟年限、被动吸烟)、饮食(进食速度、食生蒜、烹调用油、新鲜水果/蔬菜、维生素、饮酒、饮茶)、疾病史、家族史、个人因素(生活变故及性格)。采用SAS 9.2软件进行统计学分析。两组在性别、年龄、婚姻状况上分布的差异无统计学意义(P>0.05),但文化程度、职业及BMI分布的差异有统计学意义(P<0.001),见表 1。
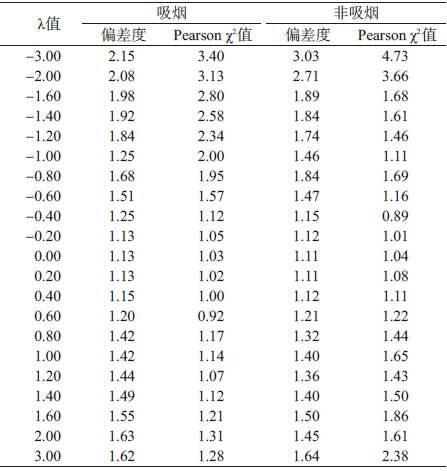
依据原则确定相对危险度模型的结构形式并拟合方程。即λ=0时,符合相乘模型者采用logistic回归模型分析;λ=1时,符合相加模型者采用线性模型分析;λ≠0且λ≠1时,符合其余作用模型者采用广义线性模型分析[3, 4]。从表 2和图 1的数据及所建立模型的偏差度曲线发现,λ=0时,偏差度值均较小,且Pearson χ2值无统计学意义(P>0.05)。据此判定本研究人群吸烟和非吸烟者原发性肺癌影响因素之间的关系偏向于相乘关系,因而采用logistic回归模型进行分析。将所有变量(吸烟者:22个;非吸烟者:21个)纳入进行多重共线性诊断,结果显示变量之间不存在共线性。
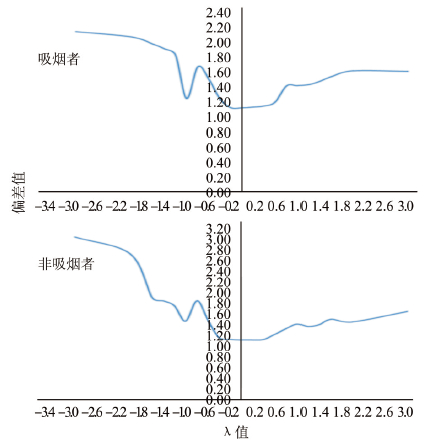 |
| 图1 吸烟者和非吸烟者数据拟合因素间相互作用模型的偏差度曲线 |
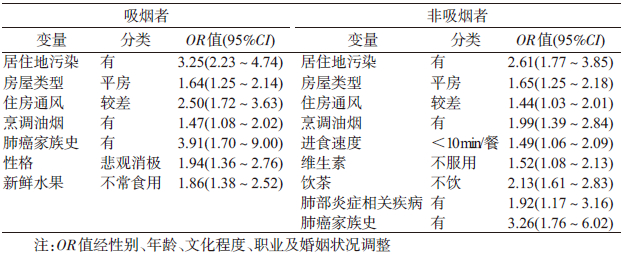
对吸烟者,将28个自变量及自变量间两两交互项共同纳入logistic多因素分析模型(逐步回归后退法),偏差度为1.06,Pearson χ2=1.02(均P>0.05),R2=0.36。结果提示居住地周围有污染企业、居住平房、住房通风情况较差、烹调过程有油烟、直系亲属有肺癌家族史、不常食用新鲜水果及具有悲观消极性格均是肺癌的危险因素,且呈现单独作用模式;对非吸烟人群,将27个自变量及自变量间两两交互项共同纳入logistic多因素分析模型(逐步回归后退法),偏差度为1.05,Pearson χ2=0.99(均P>0.05),R2=0.30。结果提示居住地周围有污染企业、居住平房、住房通风情况较差、进食速度<10 min/餐、从不服用维生素、烹调过程有油烟、肺部罹患过炎症性疾病、直系亲属有肺癌家族史及不饮茶均是肺癌的危险因素,且呈现单独作用模式(表 3)。
对纳入模型的2×2交互作用项有统计学意义且存在交互作用的因素,选用交互作用相对超额危险度(relative excess risk of interaction,RERI或 interaction contrast ratio,ICR)、交互作用归因比例(attributable proportion of interaction,API)、S指数(synergy index,S)及其95%CI指标估计其联合作用[5, 6],以ICR=0、API=0或S=1即判定为无相加交互作用。结果发现吸烟者中重度吸烟与肺部罹患过炎症性疾病呈正相乘作用,未发现相加交互作用;被动吸烟与新鲜水果对非吸烟人群原发性肺癌呈正相乘作用,未发现相加交互作用(表 4)。
当前流行病学研究数据分析存在两类意见,一是先进行单因素分析,筛选变量后将有意义变量纳入方程再进行多因素分析,进而考察应变量与自变量及自变量之间的关系;二是把所有因素均放到方程中,以矫正所有可能的混杂因素,直接探讨应变量及自变量之间的关系。应用第一种方法较为普遍,而第二种方法应用时出于拟合模型系数结果的稳定性考虑,一般都提及需要较大样本量(样本量为自变量数量的5~10倍)[7],但是因为自变量之间可能具有交互作用,分析单一自变量对应变量的贡献时可能会受其他未分析自变量的影响,故先用单因素筛选可能出现偏倚[8]。面对流行病学调查样本量和自变量均增多的情况,涌现出随机森林、树分析、贝叶斯上位效应关联等筛选变量的方法,即通过筛选减少自变量[9],接近于第二种方法。因此建议在针对当前大样本多变量的流行病学研究中,如计算机软硬件条件允许时,可采用本研究的方法将所有变量纳入方程分析;反之则应先进行变量筛选,再将筛选后的变量全部纳入方程分析。
复杂性状疾病(如肺癌)的发生发展受多因素作用,在多因素分析控制混杂因素干扰的基础上,需进一步探讨效应修饰因素的影响。Rothman认为效应修饰因素至少存在统计学、生物学和公共卫生学意义上的交互作用形式。在流行病学研究中,常常用相加模型探讨生物学和公共卫生学上的交互和联合作用[10]。本研究在环境危险因素与肺癌关系的多因素分析前,先用比数幂变换的方法探讨危险因素间的联合作用形式,结果显示无论是吸烟还是非吸烟人群,λ=0时,不仅偏差度最小,且模型的拟合优度检验均显示P>0.05,应注意当λ=-0.2或0.2时,偏差度也最小,且拟合优度检验结果也显示P>0.05,此时建议优先选择λ=0作为判断因素间联合作用形式的依据,毕竟相乘作用下使用的logistic回归模型属于成熟模型,而且便于解释结果。
复杂性状疾病各因素间的作用形式常常不清晰,在未预先判断因素之间作用形式时,直接选择logistic回归模型等相乘结构的统计模型进行分析,极易得到错误结论[11, 12]。目前认为当多个因素的共同效应等于每一因素单独效应的乘积时,因素之间联合作用的形式符合相乘模型,此时适宜使用统计学中的相乘模型(如logistic回归模型);当多个因素的共同效应等于每一因素单独效应相加之和减1时,因素间的联合作用形式符合相加模型,适宜使用统计学中的相加模型(如线性回归模型);此外如介于相乘和相加模型之间,即次相加至超相乘的中间状态[13],则推荐通过自定义不同连接函数的方法使用广义线性模型。
广义线性模型是常见的正态线性模型的直接推广[14, 15],可处理多种形式的应变量,而应变量通过连接函数g[E(Y)]与线性预测因子P建立联系,不仅确保线性关系,而且保证预测值落在应变量的各种变化内,可以解决数据过离散的问题。但也有局限性。如果自变量之间的关系可能混合存在相加和相乘时,模型无法进行处理,且模型本身的函数连接形式和参数模型的构建亦有限,尚不能完全涵盖可能出现的情况,反续又发展出广义可加模型。
Rothman等[5]认为,仅通过统计学模型中的相乘项判断交互作用,不能充分挖掘因素间作用的信息,因而提出了相加交互模型的评价指标:RERI、API和S。RERI描述归因交互作用对基础危险性的相对大小,S与其意义相同,绝对值越大,因素间的交互作用越强,两指标用于评价2个因素同时作用时的联合作用与单独作用之和的差别;API则表示因素共同存在时,发生疾病的危险归因于交互作用的比例。这些指标有利于描述因素间的协同或拮抗作用。本研究将变量两两相乘纳入方程后发现,在吸烟者中重度吸烟与肺部炎症性疾病史,非吸烟者中被动吸烟与少吃新鲜水果2个相乘项分别在方程中有统计学意义,进一步探讨该两组因素的相加交互作用,结果RERI分别为-0.56和0.38;API分别为-0.21和0.13;S分别为0.75和1.24(均P>0.05),并未发现存在因素间的协同或拮抗作用。有学者提出,分析交互作用时对样本量的要求较高,两因素联合作用的样本量至少是分析每个因素单独作用时样本量的2~4倍[16],本研究样本量为2 847例,但也未能观察到变量之间的联合作用,考虑与研究中仅分析方程中2×2交互作用项有统计学意义的因素有关,因此建议可将所有变量两两之间组合直接分析相加交互作用,而不经过相乘项进行先期判断,但增加了分析工作量。
综上分析,广义线性模型是筛选自变量与应变量关系的合适模型,并可用于研究自变量之间交互作用,有利于全面合理分析流行病学调查数据。
| [1] Wang LL, Chen CZ. Way of 'analytical thinking' on data from epidemiological studies[J]. Chin J Epidemiol, 2014, 35(6):745-748. (in Chinese) 王琳琳, 陈常中. 流行病学论文数据分析思路[J]. 中华流行病学杂志, 2014, 35(6):745-748. |
| [2] Guerrero VM, Jhonson RA. Use of the Box-Cox transformantion with binary response models[J]. Biometrika, 1982, 69:309-314. |
| [3] Moolgavker SH, Venzon DJ. General relative risk regression models for epidemiology studies[J]. Am J Epidemiol, 1987, 126:949-961. |
| [4] Tian J. The Box-Cox transform method of determining λ and SAS program[J]. J Mat Med, 2002, 15(6):481-484. (in Chinese) 田俊. 比数幂变换的λ确定方法及SAS程序[J]. 数理医药学杂志, 2002, 15(6):481-484. |
| [5] Rothman KJ, Greenland S, Walker AM. Concepts of interaction [J]. Am J Epidemiol, 1980, 112(4):467-470. |
| [6] Hosmer DW, Lemeshow S. Confidence interval estimation of interaction [J]. Epidemiology, 1992, 3(5):452-456. |
| [7] Kim PH, Chen F. Medical statistical methods[M]. 3rd ed. Shanghai:Fudan University Press, 2009. (in Chinese) 金丕焕, 陈峰. 医用统计方法[M]. 3版. 上海:复旦大学出版社, 2009. |
| [8] Hu LP, Li ZJ. Medical statistics and typical errors differentiation [M]. Beijing:Military Medical Science Press, 2003. (in Chinese) 胡良平, 李子健.医学统计学基础与典型错误辨析[M].北京:军事医学科学出版社, 2003. |
| [9] Zhang R, Chu M, Zhao Y, et al. A genome-wide gene-environment interaction analysis for tobacco smoke and lung cancer susceptibility[J]. Carcinogenesis, 2014, 35(7):1528-1535. |
| [10] Xu B. Epidemiological principles [M]. Shanghai:Fudan University Press, 2007. (in Chinese) 徐飚. 流行病学原理[M]. 上海:复旦大学出版社, 2007. |
| [11] Greenland S. Limitations of the logistic analysis of epidemiologic data [J]. Am J Epidemiol, 1979, 110(6):693-698. |
| [12] Liu DS. Comparison among logistic, log binomial and modified Poisson regression model in SAS software[D]. Zhengzhou:Zhengzhou University, 2013. (in Chinese) 刘东升. SAS软件中logistic、log-binomial及稳健Poisson回归模型的比较[D]. 郑州:郑州大学, 2013. |
| [13] Wang XD, Tian J. Generalized linear model analysis of the interaction of factors[J]. Mat Pract Theor, 2010, 40(7):112-118. (in Chinese) 王晓东, 田俊. 因素交互作用分析的广义线性模型[J]. 数学的实践与认识, 2010, 40(7):112-118. |
| [14] Fahrmeir L. Multivariate statistical modeling based on generalized linear models[M]. New York, Springer-Verlag, 1994. |
| [15] Chen XR. Generalized linear model(1)[J]. Mat Stat Manag, 2002, 21(5):54-61. (in Chinese) 陈希孺. 广义线性模型(一)[J]. 数理统计与管理, 2002, 21(5):54-61. |
| [16] Smith PG, Day NE. The design of case-control studies:the influence of confounding and interaction effects [J]. Int J Epidemiol, 1984, 13(3):356-365. |
 2015, Vol. 36
2015, Vol. 36