文章信息
- 张业武, 郭青, 王晓风, 于萌, 苏雪梅, 董言, 张春曦. 2014.
- Zhang Yewu, Guo Qing, Wang Xiaofeng, Yu Meng, Su Xuemei, Dong Yan, Zhang Chunxi. 2014.
- 空间相对危险度估计方法在传染病风险评估中的应用
- Application of spatial relative risk estimation in communicable disease risk evaluation
- 中华流行病学杂志, 2015, 36(5): 531-534
- Chinese Journal of Epidemiology, 2015, 36(5): 531-534
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2015.05.025
-
文章历史
- 投稿日期:2014-09-01
2. 新疆维吾尔自治区疾病预防控制中心信息科
2. Department of Information, Xinjiang Uygur Autonomous Regions Center for Disease Control and Prevention
疾病的发生经常受到当地自然环境和社会生活 条件的影响,因此研究疾病空间分布可为其病因及 流行因素等提供重要线索[1, 2]。而研究疾病空间分 布通常采用标点地图、疾病地区分布图和疾病传播 蔓延图等对疾病的发生、发展进行描述,并由此计算 出疾病空间分布密度、相对风险度或探测是否存在 空间聚集性等[3]。近年来疾病空间统计和推断方法 得到快速发展,而利用核密度平滑相对危险函数估 计空间相对危险度是方法之一[4, 5, 6]。为此本研究简要介绍可变带宽核密度算法在疾病空间相对危险度 估计应用原理,以及空间危险度统计学检验方法,并 结合实例说明该方法在传染病风险评估研究中的具 体应用。
基本原理
为估计疾病风险的空间变化,采用核密度平滑相对危险函数来估计其空间相对危险度。核密度估计方法为非参数估计方法,可根据给定的样本点集合,估计空间随机变量的分布密度函数。由于核密度估计从数据样本本身出发研究数据分布特征,而不必考虑数据分布先验知识,也无需对数据分布附加任何假定,因此在空间统计学理论和应用领域受到高度关注。空间相对危险度估计基本思想是采用可变带宽核密度平滑函数分别计算病例和对照空间分布的概率密度,通过比较病例和对照的密度,从而获得疾病空间分布的相对危险度,再对各空间格点的相对危险度进行统计学检验,获取各格点上的统计量及其对应的概率P值,绘制P值等值线,最终获得疾病高风险热点地图[5]。1. 可变带宽核密度平滑法:假设n个二维空间的观察点x1,x2,…,xn来自未知密度f,采用核密度平滑技术,该密度可通过公式进行估计
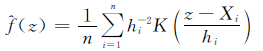
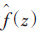 最关键环节,一般有固定带宽(fixed bandwidth)或可变带宽(adaptive bandwidth)两种选择。后者允许每个观测值有不同的带宽,较前者的估计量更具有弹性。本文采用Abramson建议的平方根法则(square-root law)选择局部带宽因子。其优点是对估计量局部偏差收敛的速度快[5, 7]。Abramson可变带宽计算公式
最关键环节,一般有固定带宽(fixed bandwidth)或可变带宽(adaptive bandwidth)两种选择。后者允许每个观测值有不同的带宽,较前者的估计量更具有弹性。本文采用Abramson建议的平方根法则(square-root law)选择局部带宽因子。其优点是对估计量局部偏差收敛的速度快[5, 7]。Abramson可变带宽计算公式
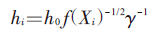
为保证结果的对称
性,Kelsall 和Diggle[6]建
议采用对数危险度函数
ρ代替原始值,即令ρ=
log(r)以便于计算或进行
统计学检验。利用样本
数据可获得总体的估计
值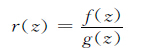 。
。
3. 空间危险度统计
学检验和P 值等值线:采
用Davies 和Hazelton[4]建
议的渐近正态法公式,计
算各空间格点上的可变
带宽危险函数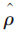 检验统计量Z(z),根据检验假设[如H0:ρ(z)=0;HA:
ρ(z)>0],获得各空间格点上统计量Z(z)所对应的
概率P 值。选择合适的P 值判断界值(如P=0.05),
绘制P值等值线,即可获得高风险热点区域地图。
检验统计量Z(z),根据检验假设[如H0:ρ(z)=0;HA:
ρ(z)>0],获得各空间格点上统计量Z(z)所对应的
概率P 值。选择合适的P 值判断界值(如P=0.05),
绘制P值等值线,即可获得高风险热点区域地图。
4. 统计学分析:使用R 软件maptools 包实现空 间随机抽样,SAS(版本9.3)软件surveryselect 过程 实现分层按比例抽样,R 软件sprr 包实现空间相 对危险度估计[5]。
实例分析 本研究数据源自中国疾病预防控制信息系统子 系统传染病报告信息管理系统中2013 年度云南省 鲁甸及周边地区其他感染性腹泻病例报告信息。其 中报告病例822 例,报告发病率为31.26/10 万,占法 定传染病报告发病总数的7.91%。1. 病例和对照的空间定位:根据病例登记的现 住址确定其空间坐标点。采用分层比例方法随机抽 取人口样本空间坐标点作为对照的空间位置,即首 先以乡镇为单位按人口数采用空间随机抽样方法, 生成同等数量的随机人口空间样本点数据库,然后 以乡镇为单位按人口比例,从空间样本点数据库中 随机抽取与病例数相等的样本点作为对照易感人群 样本点。病例和对照的空间分布见图 1
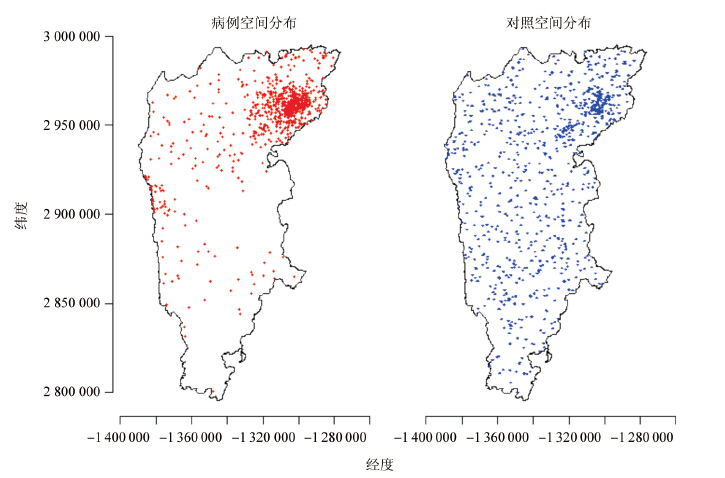 |
| 图 1 云南省鲁甸及周边地区其他感染性腹泻病例和对照人口的空间分布 |
2. 空间相对危险度估计:按照Davies 和 Hazelton[4]的方法,将病例和对照设置为相同的全局 带宽h0(global h0 ),并允许各自选择不同的平滑参 数。通过计算确定全局带宽为11 009.09,病例可变平滑参数hi( adaptive isotropic smoothing)为2 816.349, 对照可变平滑参数hi为1 944.444,以50×50 空间格 点为单位分别计算病例和对照各空间格点上的可变 带宽核密度估计值,以此估算空间格点上的对数风 险度,并绘制对数风险地图(图 2)。可见对数风险 值较高的区域主要分布在东北方位邵阳区内,其次 在中西部边缘区域,与单纯病例核密度图基本一致。
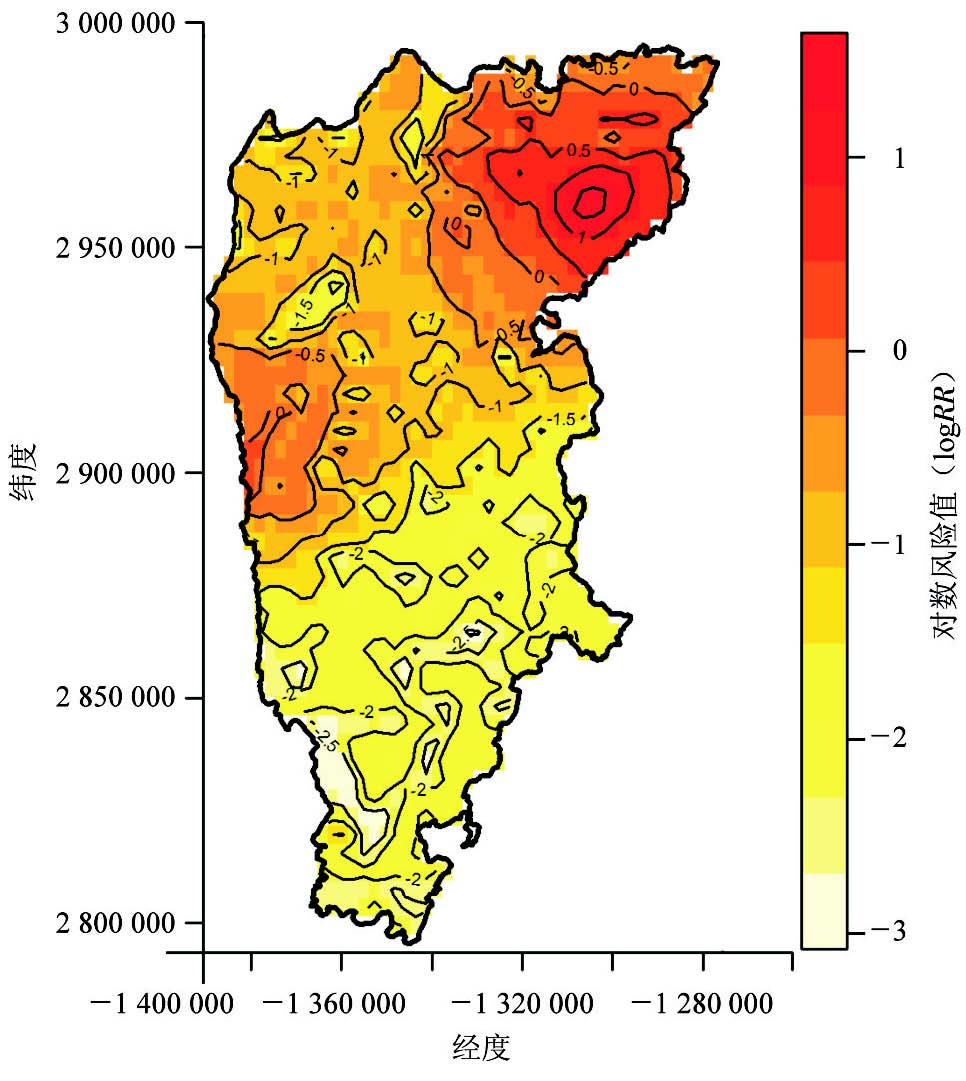 |
| 图 2 云南省鲁甸及周边地区其他感染性腹泻的可变带宽对数风险分布 |
对空间各位点的对数风险值RR>0 者采用渐近 正态法进行统计学检验,获得统计量Z(z)对应的概 率P值,以P=0.05 作为判断界值,在可变带宽对数 风险地图叠加绘制P值为0.05 等值线地图,即高风 险热点地图(图 3)。从图 3 可见,高风险区域仍集中 分布在邵阳区内。
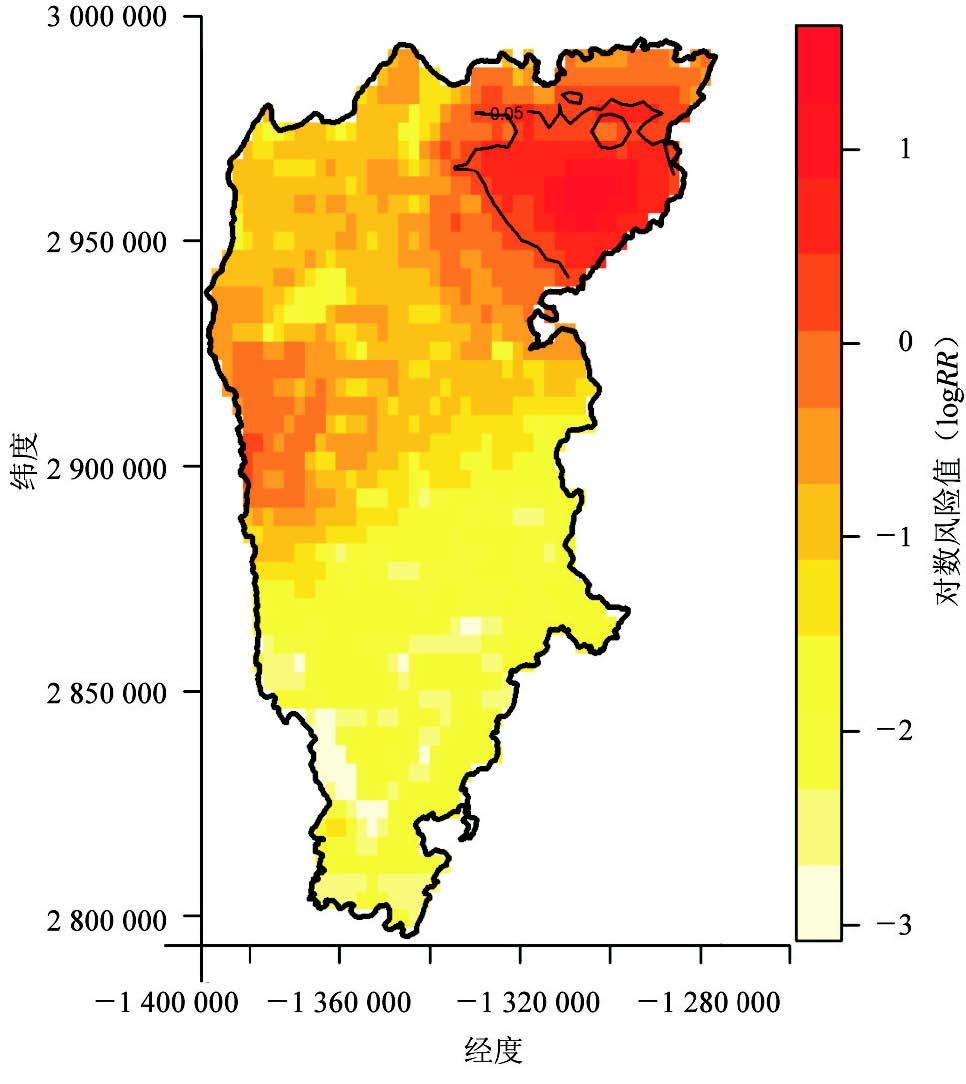 |
| 图 3 云南省鲁甸及周边地区其他感染性腹泻的对数风险热点及其合并概率等值线(P=0.05) |
空间相对危险度估计为非参数空间统计方法, 属于空间探索性分析范畴[9, 10, 11]。近年来空间相对 危险度估计方法在流行病学研究领域的应用逐渐 增多[8, 11, 12, 13]。本文将可变带宽的核密度估计方法应 用于空间相对危险度估计中,并对估计的风险区域 进行统计学检验,为确定疾病热点高发地区提供了 客观依据。
在空间统计研究领域中,如何估计密度函数至 关重要。对于核密度估计一般采用固定带宽或可变带宽。一般而言可变带宽较固定带宽的估计量更具 有弹性。在数据密集的区域,可选取较小的带宽以 降低估计的偏差;在数据稀疏的区域,可选取较大的 带宽以降低估计的方差[4]。在实际应用中, Benschop 等[12]研究发现与固定带宽比较,可变带宽 方法可矫正低密度区域中过度平滑和高密度区域中 平滑不足问题。Zhang 等[11]通过比较发现,可变带 宽方法在描述空间异质性方面能力更强,但对自定 义的平滑参数改变过于敏感,在可变带宽的算法中, 带宽对危险估计值和危险显著性检验P 值的影响 大,而对于危险估计值的标准差变化影响小。
与其他非空间流行病学研究类似,病例在空间 分布直接受到易感人群在空间分布的影响,而空间 相对危险度被认为可有效避免因易感人群空间分布 不均衡所造成的混杂因素的影响。因此,本文介绍 的相对危险函数已成为空间流行病学研究中描述疾 病分析空间变化较为常用的工具[6, 14]。
本文实例源自我国地震灾害后疾病风险评估研 究。2014 年8 月云南省鲁甸县发生6.5 级地震,为此 本研究利用2013 年度鲁甸及周边地区法定传染病 病例报告的历史信息,并获得地震灾区各相关传染 病高风险区域。高风险区域意味着某种病因或高危 险的流行因素的存在。这些危险因素可能会因为自 然灾害的原因而进一步恶化,因此本文结果提示应在所确定的高风险区域有针对性开展现场调查,找 出可能影响疾病暴发或流行的主要危险因素,有的 放矢地开展防控措施。
| [1] Rothman KJ. Epidemiology:an introduction[M]. 2nd ed. Oxford University Press, 2012. |
| [2] Li LM. Epidemiology[M]. 6nd ed. Beijing:People's Medical Publishing House, 2007. (in Chinese) 李立明. 流行病学[M]. 6版. 北京:人民卫生出版社, 2007. |
| [3] Waller LA, Gotway CA. Applied spatial statistics for public health data[M]. Hoboken, New Jersey: John Wiley & Sons, 2004. |
| [4] Davies TM, Hazelton ML. Adaptive kernel estimation of spatial relative risk[J]. Stat Med, 2010, 29(23):2423-2437. |
| [5] Davies TM, Hazelton ML, Marshall JC. Sparr:Analyzing spatial relative risk using fixed and adaptive kernel density estimation in R[J]. J Stat Softw, 2011, 39(1):1-14. |
| [6] Kelsall JE, Diggle PJ. Non-parametric estimation of spatial variation in relative risk[J]. Stat Med, 1995, 14(21/22):2335-2342. |
| [7] Abramson IS. On bandwidth variation in kernel estimates-a square root law[J]. Ann Statist, 1982, 10(4):1217-1223. |
| [8] Bithell JF. An application of density estimation to geographical epidemiology[J]. Stat Med, 1990, 9(6):691-701. |
| [9] Harpole JK, Woods CM, Rodebaugh TL, et al. How bandwidth selection algorithms impact exploratory data analysis using kernel density estimation[J]. Psychol Meth, 2014, 19(3):428- 443. |
| [10] Cislaghi C, Biggeri A, Braga M, et al. Exploratory tools for disease mapping in geographical epidemiology[J]. Stat Med, 1995, 14(21/22):2363-2381. |
| [11] Zhang ZJ, Davies TM, Gao J, et al. Identification of high-risk regions for schistosomiasis in the Guichi region of China:an adaptive kernel density estimation-based approach[J]. Parasitology, 2013, 140(7):868-875. |
| [12] Benschop J, Hazelton ML, Stevenson MA, et al. Descriptive spatial epidemiology of subclinical salmonella infection in finisher pig herds:application of a novel method of spatially adaptive smoothing[J]. Vet Res, 2008, 39(1):2. |
| [13] Carlos HA, Shi X, Sargent J, et al. Density estimation and adaptive bandwidths:a primer for public health practitioners[J]. Int J Health Geogr, 2010, 9:39. |
| [14] Clough HE, Fenton SE, French NP, et al. Evidence from the UK Zoonoses Action Plan in favour of localised anomalies of Salmonella infection on United Kingdom pig farms[J]. Prev Vet Med, 2009, 89(1/2):67-74 |
 2015, Vol. 36
2015, Vol. 36


