文章信息
- 陈金宝, 邱李斌, 王北琪, 曾洁, 陈征. 2014.
- Chen Jinbao, Qiu Libin, Wang Beiqi, Zeng Jie, Chen Zheng. 2014.
- 固定点处组间生存率比较的统计检验法
- Statistical methods for comparing survival rates at a fixed time point
- 中华流行病学杂志, 2015, 36(2): 186-188
- Chinese Journal of Epidemiology, 2015, 36(2): 186-188
- http://dx.doi.org/10.3760/cma.j.issn.0254-6450.2015.02.019
-
文章历史
- 投稿日期:2014-09-27
疾病预后分析是临床流行病学的重要研究内容,其中估计生存率常用的方法是寿命表或是Kaplan-Meier估计,如胃癌患者治疗后5年(t=5)的生存率为25%[S(t)=0.25]。同样,不同暴露环境/处理方式下两样本生存率的比较也是重要的研究问题,通常采用Log-rank检验推断两生存曲线整体间 (整个观察期间)是否有差异,如放疗组和放化疗联合组在预后5年生存率有无差异,若生存曲线出现交叉情况,由于不满足成比例假设,则Log-rank检验不适用[1, 2]。例如,在一项胃肠道肿瘤治疗法的8年随访研究中[1],对局部无法切除的胃癌患者分别进行单纯化疗和联合放化疗,由于两条生存曲线大约在第3年时交叉(图 1),并经Grambsch-Therneau检验[2],两组累积危险率不成比例(χ2=13.10,P<0.001),因此Log-rank检验结果(χ2=0.23,P=0.630)不可靠。在出现生存曲线交叉的情况下,李慧敏等[3]建议采用Two-stage检验可得到两组间生存率的差异有统计学意义(P=0.025)的结果,结合图 1,依旧很难给出在整体上哪种治疗法生存率更高的结论,并且在临床研究中更加感兴趣是第3、5年等某些特别/固定时间点上两种治疗法疗效的预后差异,如放疗和化疗在第1、3、5年的生存率是否有差异。
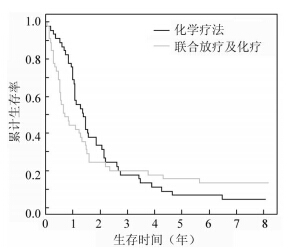 |
| 图 1 胃癌患者分别进行单纯化疗和联合放疗 及化疗的生存曲线 |
Weeda等[4]在生存曲线交叉时,使用Z检验比较第3年时的组间差异,但针对带右删失的生存数据采用Z检验并不适合。针对上述存在的问题,本文介绍5种在固定点比较生存率的统计推断方法,分别为经典法、对数转换法、cloglog转换法、反正弦法和logit转换法,并结合实例分析说明。 基本原理
这里主要考虑两条生存曲线在某个固定时间点的比较。假设第k组有样本量nk,其中k=1,2,tki表示第k组中的第i个事件发生的时间,且tk1<tk2<…<tkn,dki表示第k组中在时间tki发生事件数,Yki表示第k组在时间点tki风险人数。Kaplan-Meier估计及其方差分别表示为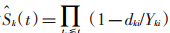 和
和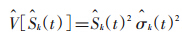 ,其中
,其中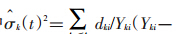 -dki),累积危险率及其方差估计值分别是
-dki),累积危险率及其方差估计值分别是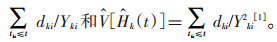
比较在时间点t的两组生存率,原假设H0是在某固定时间点t,两组生存率相等,即S1(t)=S2(t)。以下提供5种检验法[5]。
1. 经典法:
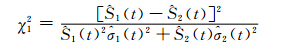
在原假设成立下,此检验的统计量近似服从自由度为1的χ2分布。类似的可基于危险率函数Nelson-Aalen估计,构建检验统计量为

检验统计量是基于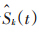 或
或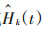 的某个恰当转换(或说函数)φ,因此通过delta法,可得
的某个恰当转换(或说函数)φ,因此通过delta法,可得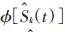 近似服从均值为
近似服从均值为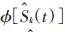 ,方差为
,方差为 的正态分布。通过危险率Nelson-Aalen估计的转换也可以得到类似结果。对于生存函数的Kaplan-Meier估计来说,基于方差的稳健转换被用来更好的呈现转换过后的生存函数的置信区间[6]。在此,可以认为在原假设成立下,以下一系列的转换得到的统计量都近似服从χ2分布。
的正态分布。通过危险率Nelson-Aalen估计的转换也可以得到类似结果。对于生存函数的Kaplan-Meier估计来说,基于方差的稳健转换被用来更好的呈现转换过后的生存函数的置信区间[6]。在此,可以认为在原假设成立下,以下一系列的转换得到的统计量都近似服从χ2分布。
2. 对数转换:基于Nelson-Aalen估计值,对生存函数进行对数转换后得到检验统计量
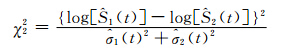
3. cloglog转换:即基于生存函数的log[-log(·)]转换,通常用于构建生存函数的置信区间[6]和置信带[7],在小样本量(如n=25),且删失率高(如50%)时,此转换法也可给出准确覆盖率作为95%CI。在原假设成立的条件下,检验统计量为
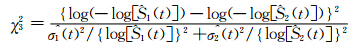
4. 反正弦转换:此统计量的构造是基于反正弦根(arcsine-square root)的转换法,同cloglog转换法也可给出小样本95%的覆盖率作为其CI[6]。统计量为
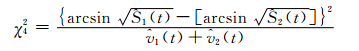

5. logit转换:生存率一般不服从正态分布,logit转换有助于调整数据的形态,且可以较好地处理非线性相关的指标与增长性的分析。统计量为

本文提供2个实例(其中例1表现为生存曲线交叉,例2为生存曲线前期基本重合,后期分开) 比较上述5种固定点生存率统计方法间的差异。
【例1】 一项胃肠道肿瘤治疗法的随访研究中共计90例胃癌患者,分别进行单纯化疗和联合放化疗,每组样本量为45例(右删失率分别为4.4%和13.3%),终点事件为死于胃癌,到研究截止时间为止未发生终点事件的胃癌患者为右删失(图 1)。两组的中位生存时间分别为499 d和254 d。表 1中5种检验方法对两条生存曲线几个时间点处的比较结果,均显示两组间第1年生存率的差异有统计学意义,在治疗胃肠道肿瘤上单纯化疗的生存率较联合放化疗的生存率高,而第3、5年生存率的差异无统计学意义。若用Log-rank检验或Two-stage检验均很难给出合理的结果。
【例2】 一项预防腺性息肉瘤的研究[8],对曾患结肠直肠腺瘤的患者分别服用万络和安慰剂,终点事件是发生心血管事件(如心脏病及中风),到研究截止时尚未发生终点事件的结肠直肠腺瘤患者为右删失,结果显示入组时两组患者出现心血管事件的概率基本一致,但18个月后服用万络的患者出现心血管事件的概率高于服安慰剂者。由于原文数据无法获得,因此参照Royston和Mahesh[9]的方法模拟 了Lagakos[8]文中的临床数据(图 2)。万络组和安慰剂组的样本量分别为132人和130人,对应右删失率为22.0%和37.7%,中位生存时间为9.71个月和10.04个月。Log-rank检验结果为两组间整体的差异无统计学意义(χ2=1.48,P=0.223),但由于Grambsch-Therneau检验显示两组不满足比例假设(χ2=4.45,P=0.035)[2],图 2同时显示两组短期(约18个月前)和长期(约18个月后)效应似乎不同,因此Log-rank检验结果不可靠。采用5种固定点生存率差别检验法可发现(表 2),两组间第12个月和第18个月生存率的差异均无统计学意义,而在第30个月时差异均有统计学意义。但是在长期中的第24个月时生存率的差异除对数转换法和logit转换法无统计学意义外,其他3种方法的结果均有统计学意义,其中cloglog转换法效果最好[6],已有模拟研究表明该法在第一类和第二类错误上综合效果最佳[5],本文以cloglog的检验效果为准,可以认为第24个月的结果有统计学意义。结果显示在第18个月前两组疗效无差异,而在第18个月后万络组的生存率相对较低,即服用万络患者短期内安全,但长期服用有风险。
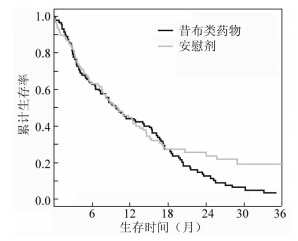 |
| 图 2 结肠直肠腺瘤患者分别服用昔布类药物 和安慰剂的生存曲线 |
结语:两条生存曲线比较时,在满足了两组累积危险率成比例假设的前提下,Log-rank检验为最佳选择,否则Two-stage检验法更合适,但有特殊,如前述2个实例,当难以选择两条生存曲线整体间比较的检验法时,或者仅需要比较某些固定点处组间生存率差异时,可使用本文以上介绍的固定点时刻生存率比较检验法。其中,如Klein等[5]通过Monte Carlo模拟研究表明,结合第一类和第二类错误的结果,cloglog转换的检验性能最好,其次是反正弦转换、对数转换和logit转换,经典法相对较差,与采用这5种转换方法计算生存率的CI值时分析结果类似[6],建议使用cloglog转换法。
| [1] Klein JP,Moeschberger ML. Survival analysis:techniques for censored and truncated data. 2nd ed[M]. New York(NY):Springer,2003. |
| [2] Grambsch P,Therneau T. Proportional hazards tests and diagnostics based on weighted residuals [J]. Biometrika,1994,81:515-526. |
| [3] Li HM,Han D,Chen Z,et al. Comparison and choice of statistical inference methods for two crossing survival curves [J]. Chin J Health Stat,2013,30(5):668-672. (in Chinese) 李慧敏,韩栋,陈征,等.生存曲线交叉时统计推断的比较和选择[J]. 中国卫生统计,2013,30(5):668-672. |
| [4] Weeda VB, Murawski M,McCabe AJ,et al. Fibrolamellar variant of hepato-cellular carcinoma does not have a better survival than conventional hepato-cellular carcinoma-Results and treatment recommendations from the Childhood Liver Tumour Strategy Group (SIOPEL) experience [J]. Eur J Cancer,2013,49(12):2698-2704. |
| [5] Klein JP,Logan B,Harhoff M,et al. Analyzing survival curves at a fixed point in time [J]. Stat Med,2007,26:4505-4519. |
| [6] Xiang YB,Gao YT,Jin F,et al. Five methods for the estimation of confidence intervals on survival rate [J]. Chin J Epidemiol,1995,16(5):306-309. (in Chinese) 项永兵,高玉堂,金凡,等.生存率置信区间的五种估计方法[J]. 中华流行病学杂志,1995,16(5):306-309. |
| [7] Borgan Ø,Liestøl K. A note on confidence intervals and bands for the survival curve based on transformations[J]. Scand J Stat,1990,17:35-41. |
| [8] Lagakos SW. Time-to event analyses for long-term treatments-the APPROVe trail [J]. N Engl J Med,2006,355:113-117. |
| [9] Royston P,Mahesh KBP. The use of restricted mean survival time to estimate the treatment effect in randomized clinical trials when the proportional hazards assumption is in doubt [J]. Stat Med,2011,30(19):2409-2421.. |
 2015, Vol. 36
2015, Vol. 36



