Citation

Zhou Yuhao, Wu Siyuan, Ren Xiaozhe, Li Hongjin, Li Shu, Yan Tianying. Effects of salt fraction on the Na⁺ transport in salt-in-ionic liquid electrolytes[J]. Chin. Chem. Lett., 2025, 36(6): 110048  

Yuhao Zhou, Siyuan Wu, Xiaozhe Ren, Hongjin Li, Shu Li^*, Tianying Yan^*     

The increasing demand of the high volume and mass energy density batteries for mobile applications like (hybrid) electric vehicles and laptops calls for the next-generation energy storage devices [1,2]. Sodium (Na) ion batteries (SIBs) are expected to be one of the most promising candidates due to Na’s high abundance in the earth’s crust, low cost, as well as its relatively negative standard potential (−2.71 V vs. SHE) and high theoretical capacity (1166 mAh/g) [3-7]. However, conventional organic electrolytes currently applied in SIBs, like carbonate esters and ethers, regardless of their good ionic conductivity, sufficient salt solubility and low viscosity [8-10], suffer from high flammability and low resistance to electrochemical reduction, which arise safety concern and constrain the coulombic efficiency of SIBs [11-13].

Ionic liquids (ILs), also named room-temperature molten salts, which typically consist of organic cations and anions and are generally in liquid phase at ambient temperature [14], possess the superiority of non-flammability, negligible volatility, designable nature, and high thermal stability [15-17]. Specifically, ILs doped with sodium salts have been extensively researched as electrolyte for SIBs [18-20]. Primarily, such salt-in-ionic liquid electrolytes (SILEs) can function stably and even possess better transport properties at high temperature that organic solvent reaching its ignition point, and thus guarantee the safety of SIBs under harsh conditions [21]. Besides, SILEs have wide electrochemical window, which provides well-behaved cycle stability even in direct contact with Na anode [22].

Despite these advantages, the ionic conductivity (σ) of SILEs is relatively low compared to organic electrolytes, originating from the strong coulombic interactions between cations and anions, especially at low temperature, which leads to large internal resistance in such electrolytes [23]. While some efforts have been put on to increase σ like substitution of functional groups thanks to the designing nature of ILs [24], adjusting the salt fraction of SILEs is considered another simple but feasible scheme [25]. Via molecular dynamics (MD) simulations, Molinari and coworkers [26] observed a low and even negative conductivity of Na⁺ in NaFSI−C₃C₁PyrrFSI (C₃C₁Pyrr⁺: N-methyl-N-propylpyrrolidinium, FSI⁻: bis(fluorosulfonyl)imide) at low molar fraction of NaFSI, i.e., x(NaFSI). They further demonstrated that the conductivity of Na⁺ increases with higher molar fraction of Na⁺ in the SILE, which is also supported both experimentally [27] and computationally [28]. It should be kept in mind that the higher ionic conductivity of Na⁺, i.e., σ_Na⁺ = σ × t_Na⁺, is desired, because other ions are electrochemical inert during SIB operation. A negative transference number of Na⁺ (t_Na⁺) means that Na⁺’s tend to migrate with anions during SIB operation, which increases internal resistance of such SILEs.

Generally, adding more salt will sacrifice σ of SILEs due to the stronger interaction between Na⁺ and anions, though accompanying with higher t_Na⁺. Matsumoto and coworkers found in NaFSI−C₃C₁PyrrFSI that σ_Na⁺ was highest when the molar fraction of NaFSI was in the range of 0.2–0.4 at temperature T=353 K [29], which was in agreement with their earlier observation that the highest rate performance was achieved with x(NaFSI)=0.4 at T = 363 K [30]. Indeed, the rate performance of the SIB is determined by σ_Na⁺, rather than σ, as only Na⁺’s shuttle rapidly between cathode and anode during the charge/discharge process. Thus, it is of interest to study how σ_Na⁺ varies with the molar fraction of Na salt in SILEs [31].

In this study, we use molecular dynamics (MD) simulations to investigate σ_Na⁺ in the SILE, (NaFSI)_x(EMIMFSI)_1-x (EMIM⁺: 1-ethyl-3-methylimidazolium), with various x from 0.1 to 0.7 at T = 298 K. The reason that we choose this specific SILE is that it was found ILs with imidazolium-based cations often possess higher ionic conductivity compared to other cations [32,33], while FSI⁻-based ILs also exhibit better transport properties than other anions [34]. MD simulations were carried out to calculate σ, t_Na⁺ and σ_Na⁺, and their correlations with the liquid structure at different x(NaFSI) are discussed. Methods and force field parameters are summarized in Supporting information.

Table 1 lists the ionic conductivities and the transference numbers of Na⁺ of the SILE (NaFSI)_x(EMIMFSI)_1-x with different molar fraction x at T = 298 K. It can be seen that the simulated ionic conductivities are in good agreement with the experimental measurements, demonstrating the reasonable force field applied in the MD simulations, which can also be seen from the good consistency between the simulated and experimental mass densities in Table S5 (Supporting information). Apart from that, Table 1 shows that t_Na⁺ increases monotonically, while σ decreases monotonically with higher x. At low x=0.1, t_Na⁺ is even negative. Recent study also demonstrated the improved t_Na⁺ in SILEs with higher Na⁺ concentration [28]. Such monotonically increasing t_Na⁺ with higher x is expected, because in the high x, Na⁺’s become the dominant cations that contribute to σ, while the center-of-mass of SILE remains static in the MD simulation [35].

Table 1

Table 1 Comparisons between simulated and experimental ionic conductivity (mS/cm), the simulated ionic conductivity of Na+ (σNa+), and the simulated transference number of Na+ (tNa+) of the SILE (NaFSI)x(EMIMFSI)1-x at T=298 K.

Table 1 Comparisons between simulated and experimental ionic conductivity (mS/cm), the simulated ionic conductivity of Na+ (σNa+), and the simulated transference number of Na+ (tNa+) of the SILE (NaFSI)x(EMIMFSI)1-x at T=298 K.

It can be seen from Table 1 that σNa+ is the balance between monotonically decreasing σ and monotonically increasing tNa+ with x, and peaks at x=0.5. For a SILE in SIB, it is desired to optimize σNa+ to improve the rate performance [38]. Thus, it is of interest to investigate the origin of the highest σNa+, which occurs at x=0.5. In order to detect the impact of x on the transport of Na+, we further partition the individual contribution of σNa+ to the self contribution σNa+s as the result of the displacement of the same Na+, the distinct contribution σNa+−Na+d for the cross correlations among different Na+’s, as well as the cross correlations σNa+−EMIM+ and σNa+−FSI− between Na+ and other ions, respectively. The above individual contributions to σNa+ at different x are shown as histograms in Fig. 1, which also presents σ and σNa+ as lines for comparison.

Figure 1

Download: JPG larger image

Fig. 1. Ionic conductivity σ (black line) of (NaFSI)x(EMIMFSI)1-x and individual contributions σNa+ind to σNa+ (red line) at various x, including self contribution of Na+ 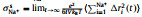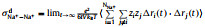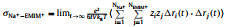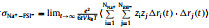(purple), distinct contribution of Na+-Na+ (yellow), and cross contributions of Na+-EMIM+ (orange) and Na+-FSI− (green), respectively, in which NEMIM+ and NFSI− denote the number of EMIM+ and FSI− in the PBC cell. The error bar denotes the standard deviation.

In the Nernst-Einstein limit, only σNa+s contributes to σNa+, i.e., σNa+ = σNa+s, because motions of different ions are independent and, thus, uncorrelated. Fig. 1 shows that σNa+s is peaked at x=0.3, as a balance between the number of specific charge carries, Na+’s, and the decreasing mobility with higher x. Apart from that, σNa+−Na+d, σNa+−EMIM+, and σNa+−FSI− are all negative for all the inspected x, and the resulting σNa+ is much smaller than σNa+s. Thus, there exist strong ionic correlations that deviate much from the Nernst-Einstein relation, as expected in SILEs solely composed of bare ions [39].

Generally, the negative σNa+−Na+d and σNa+−EMIM+ denote that different cations tend to migrate along opposite directions under external electric field, while the negative σNa+−FSI− denotes Na+ and FSI− tend to migrate together along the same direction under external electric field. Such strongly correlated ionic motion may be understood from the coordination structure, negatively charged cluster, such as [Li+(TFSI−)2]− in SILE of lithium salt, as discussed by Schonhoff [40], and also found in MD simulations [41].

Figs. 2a and b show a series of center-of-mass (cm) radial distribution functions between Na⁺ and FSI⁻ and atomistic site-site radial distribution functions between Na⁺ and O-atoms on FSI⁻, as well as corresponding cumulative distribution functions, for which x=0.1, 0.3, 0.5, and 0.7 respectively. It can be seen from Figs. 2a and b that while are similar for different x, the first peaks at 3.50 Å and 2.55 Å are both depressed from 8.9 to 4.1 and from 13.2 to 7.7, respectively. The difference is that increases at the second peak of with increased x, but is slightly reduced at the first minimum in of 3.75 Å. Such changes suggest that the average number of coordination O-atom per FSI⁻ decreases, i.e., the proportion of the monodentate coordinated Na⁺ by FSI⁻ increases with x [28], which can be also viewed from the isodensity spatial distribution of Na⁺’s around a central FSI⁻, as shown in Figs. 2c-f. Because the spatial distribution is highly anisotropic, the selected density of Na⁺ corresponds to 2 times the first peak values of of the individual x’s in Fig. 2a. It is clear that FSI⁻ tends to donate two oxygen atoms to coordinate with Na⁺ in a bidentate manner for all x’s, because the green cloud between two sulfonyl groups is the largest. With increasing x, the additional Na⁺’s start to coordinate with FSI⁻ in a monodentate manner, as small green clouds appear near one sulfonyl group of the central FSI⁻.

Figure 2

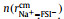
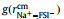
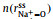
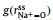
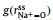
Download: JPG larger image

Fig. 2. (a) Center-of-mass radial distribution functions (solid lines) between Na+ and FSI−, 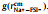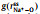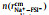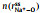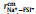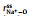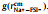. (b) Atomistic site-site radial distribution functions (solid lines) of between Na+ and O-atoms on FSI−, with x=0.1 (black), 0.3 (red), 0.5 (green), and 0.7 (blue), as well as corresponding cumulative distribution functions (dotted lines), and , in which and denote the center-of-mass distance between Na+and FSI− and the atomistic site-site distance between Na+ and O-atoms on FSI−, respectively. Isodensity spatial distributions of Na+ (green cloud) around a central FSI− for x=0.1 (c), 0.3 (d), 0.5 (e), and 0.7 (f), in which FSI−’s are represented by ball-and-stick model with O-atoms (red), N-atoms (blue), S-atoms (yellow), and F-atoms (pink), respectively. The selected densities of Na+ correspond to 2 times the first peak values of in (a) of the individual x’s.

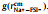
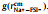
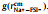
In order to further characterize the coordination structure of Na⁺ corresponding to the double-peak pattern of in Fig. 2a, we calculated two-dimensional probability distributions, P(, ), at x=0.1, 0.3, 0.5, and 0.7, respectively, as shown in Fig. 3. It is obvious from Figs. 3a-d, the first peaks of at 3.5 Å in Fig. 2a correspond to the SS vector from an S atom to the other S on an FSI⁻ coordinated with Na⁺ being almost perpendicular to the Na⁺cm⁻ vector from the cm of this FSI⁻ to its coordinating Na⁺. Such observation indicates that the cm of FSI⁻ is closer to Na⁺ when it donates two sulfonyl groups simultaneously to coordinate with Na⁺, i.e., the bidentate coordination manner, as shown in Fig. 3e (3.53 Å). Similar observation has been also found in SILE with lithium salt [42]. Such FSI⁻ in the bidentate manner has stronger bonding with Na⁺, which is unfavorable for the transport of Na⁺. The second peaks between 4.0 Å and 5.0 Å of in Fig. 2a correspond to the monodentate manner, where the angle between SS vector and Na⁺cm⁻ vector is about 30° to 60°. Although the interaction between an individual FSI⁻ and Na⁺ at this time is weaker than that of the bidentate coordination of FSI⁻ and Na⁺, FSI⁻ with the monodentate manner allows easy coordination with several Na⁺’s at the same time, so that the overall ionic network may be more compact.

Figure 3

Download: JPG larger image

Fig. 3. Two-dimensional probability distribution, P(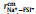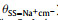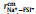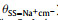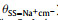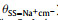, ), at x=0.1 (a), 0.3 (b), 0.5 (c) and 0.7 (d), in which denotes the distance between Na+and the cm of FSI−, and denotes the angle between the SS vector from an S atom to the other S on an FSI− coordinated with Na+ and the Na+cm− vector from the cm of this FSI− to its coordinating Na+. The value of P(, ) corresponds to the lower-left color bar; (e) Schematic coordination structure of Na+ and FSI−’s, taken from the system of x = 0.5, in which Na+ (purple), O-atoms (red), N-atoms (blue), S-atoms (yellow), F-atoms (pink) and the cm (white) of FSI− are represented by ball-and-stick model, respectively. and are shown with pink and green numbers.

As x increases from 0.1 to 0.7, the number ratio of FSI⁻ to Na⁺ decreases from 10:1 to 10:7. Intuitively, due to the strong electrostatic interaction, there should be more FSI⁻’s in the first solvation shell of Na⁺ at low x. In this case, coordinating FSI⁻’s tend to take the monodentate manner in order to reduce the mutual repulsion among them. However, it can be viewed vividly from Fig. 3 that the actual scenarios are counter-intuitive. At high x, the monodentate coordinating FSI⁻ with 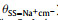from 30° to 60° increases, and such observation is consistent with Fig. 2. The effect is two-fold. On one hand, the increased monodentate coordination between Na⁺ and FSI⁻ improves Na⁺ transport due to the weaker coordination; On the other hand, the increased monodentate coordination also promotes the simultaneous association of an FSI⁻ with several Na⁺’s, which cause percolation among Na⁺’s and FSI⁻’s, thereby hindering Na⁺ transport. More severely, such arrangement may cause large aggregates (AGGs) that make the Na⁺ inside essentially immobile [23], due to the blockage of the Na⁺ pathway.

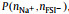
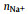
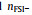
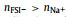
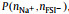
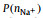
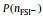
To clarify the influence of x on the distribution of AGGs in the SILEs, Fig. 4 shows the normalized two-dimensional probability distributions, , of the AGGs formed by Na⁺ and FSI⁻ at x = 0.1, 0.3, 0.5, and 0.7 respectively, in which and represents the number of Na⁺ and FSI⁻ in a specific aggregate. It can be seen from Fig. 4 that most AGGs are negatively charged, which are composed of more FSI⁻ than Na⁺ with . This is in agreement with the MD simulations by Molinari et al. [26]. The most probable AGG is [Na⁺(FSI⁻)₃]²⁻ for x = 0.1 and 0.3, for which are 0.456 and 0.279, respectively. This is reasonable because at low x there are much more FSI⁻’s than Na⁺’s, and FSI⁻’s compete to coordinate with Na⁺’s due to the strong electrostatic interaction among them. It is of interest to note that this is in contrast to [Li⁺(TFSI⁻)₂]⁻ in SILE of lithium salt [40], due to the bulkier Na⁺ comparing to Li⁺. At higher x, it can be seen from Figs. 4b and c that larger AGGs emerge. Specifically, for x = 0.3 and 0.5, the SILEs show bimodal distributions, which can be seen clearly in and . On the other hand, there is only a single peak at large AGGs for x=0.7 in Fig. 4d. Thus, at x = 0.7 the SILE consists of percolating ion network that essentially traps all the Na⁺’s. This change in the electrolytic structure can also be observed in the interference part of the X-ray scattering intensity, I(q), of the SILEs shown in Fig. S3 (Supporting information), in which there exists almost no pre-peak around scattering length q = 0.4 Å⁻¹ with x = 0.1, but such pre-peak becomes rather sharp with higher x. The existence of pre-peak indicates the inhomogeneous structure, manifested in the AGGs that cause uneven densities in the electrolyte with higher x (Fig. 4).

Figure 4

Download: JPG larger image

Fig. 4. Two-dimensional probability distributions, 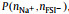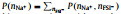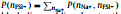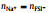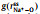, of the number of Na+ and the number of FSI− in the AGGs formed by Na+ and FSI− as heat map in x=0.1 (a), 0.3 (b), 0.5 (c), and 0.7 (d), respectively. The corresponding one-dimensional probability distributions of and are also shown as histograms in semi-log style. The black diagonal line denotes the AGGs with symmetric compositions, i.e., of equal number of Na+’s and FSI−’s. An AGG is defined to be the inter-connected Na+ and FSI−, in which the distance between Na+ and the oxygen atom on FSI− is smaller than the first minimum of in Fig. 2b.

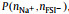
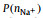
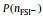
It is of interest to note that at x = 0.5, splits to two major distributions, one consisting of small AGGs with a few Na⁺’s, while most Na⁺’s are pulled in the large AGGs in which the transport of Na⁺’s is hindered. On the other hand, the small portion of Na⁺’s that drift away from the large AGGs can be considered to be more "free", according to the mean-field theory proposed by Kornyshev and co-workers [23]. This is because most of FSI⁻’s exist in the percolating ion network, as comparing and in Fig. 4c for higher n’s, so that the remaining "free" Na⁺’s transport with the overall reduced negative σ_{Na⁺−FSI⁻} in Fig. 1. Thus, the balance between the portion of "free" Na⁺ and the accumulation of FSI⁻’s in the percolating ion network is important to achieve high σ_Na⁺ in SILEs for SIBs.

In summary, we use MD simulations to investigate the SILE, (NaFSI)_x(EMIMFSI)_1-x, with various x from 0.1 to 0.7 at T = 298 K. MD simulations show that though σ decreases monotonically with increasing x, σ_Na⁺ peaks at x = 0.5. In the practical operation of SIBs, an appropriate molar fraction of Na salt is desired. Thanks to the wide electrochemical window and safety of ionic liquids electrolytes, it enables SIBs to be operated at higher voltage and, thus, high energy density can be stored and delivered. However, the application of SILEs is limited by its low ionic conductivity and thus it is difficult to be operated at high power density. The current study highlights the impact of molar fraction of Na⁺ in SILEs, and emphasizes the design of the electrolyte with high σ_Na⁺ because Na⁺ is the only electrochemically active species in SILEs. We hope this work will contribute on the optimization of SILEs with fast transport of Na⁺ to support high rate performance of SIBs.

The authors declare that they have no competing interests.

Yuhao Zhou: Data curation, Formal analysis, Investigation, Software, Validation, Visualization, Writing – original draft. Siyuan Wu: Data curation, Formal analysis, Methodology, Software, Validation. Xiaozhe Ren: Data curation, Formal analysis, Investigation, Software, Visualization, Writing – review & editing. Hongjin Li: Data curation, Software, Validation, Visualization. Shu Li: Formal analysis, Investigation, Methodology, Project administration, Supervision, Validation, Visualization, Writing – review & editing. Tianying Yan: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Software, Supervision, Validation, Writing – original draft, Writing – review & editing.

This study is supported by National Natural Science Foundation of China (No. 22273040).

Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.cclet.2024.110048.