b Key Laboratory of Computer Vision and Systems (Ministry of Education), School of Computer Science and Engineering, Tianjin University of Technology, Tianjin 300384, China;
c Hubei Key Laboratory of Low Dimensional Optoelectronic Materials and Devices, Hubei University of Arts and Science, Xiangyang 441053, China;
d ARC Centre of Excellence for Electromaterials Science, Intelligent Polymer Research Institute, Australia Institute for Innovative Materials (AIIM), Innovation Campus, University of Wollongong, Wollongong 2519, Australia
With the rapid development of society and economy, the exploration of advanced batteries with high performance remains a universal issue [1-3]. Due to the high power density, large reversible capacity and long cycle life, rechargeable Li-ion batteries have drawn much attention and achieved great success in various fields, such as portable electronic devices and electric vehicles [4-7]. However, the large-scale commercial manufacturing of Li-ion batteries is limited by the rare lithium resources and high cost in industrial production, thus the increasing energy demand cannot be meet [8]. It is desirable to develop other Alkali metal-ion batteries composed of abundant elements. Hence, Na- and K-ion batteries are emerged as two appealing alternatives to Li-ion batteries for application in electrochemical energy storage devices [9-14]. Compared with Li-ion batteries, although the intercalation/deintercalation mechanisms are similar, the Na/K-ion batteries have unique physical and chemical properties, including redox potential, ionic radius and weight [15, 16]. Many anode materials showing excellent Li-ion storage capability might no longer be suitable for Na/K-ion batteries.
In recent years, the discovery of graphene has stimulated enthusiasm toward the development of two-dimensional (2D) materials [17-20]. These exfoliated 2D materials are expected to offer new opportunities to design anode materials because of the planar structural features and large surface areas [21]. Until now, numerous 2D materials such as TMOs [22], TMDs [23-25] and MXenes [26-28] have been confirmed to be potential candidates for Na/K-based batteries. Nevertheless, the performance of Na/K-ion batteries still suffer from the drawback of energy density. Most of these 2D anodes show low theoretical capacities, ranging from 300 mAh/g to 1000 mAh/g. In this regard, metal-free 2D anode materials, composed of B, C, N, Si, P or S element, are particularly attractive in batteries [29-36]. For instance, Xu et al. [31] experimentally synthesized C3N sheets and explored their performances for anode materials in Li-ion batteries. Bhauriyal et al. [32] further found that C3N monolayer could serve as promising anode materials for Na/K-ion batteries. Other theoretical studies also reported that the BP [33], Si3C [34], PC3 [35] and B2S [36] anode materials exhibited both high storage capacity and fast ion diffusivity. Therefore, searching for new metal-free 2D anode materials with high capacity and fast kinetics is urgent for Na/K-ion batteries.
Recently, graphene-like BC3 sheet has been successfully fabricated on the NbB2 (0001) surface [37], showing good promise for applications as gas sensors, photocatalysts, thermoelectric and hydrogen storage materials [38-43]. Although few works have been carried out on the energy storage based on graphite-like BC3 electrode, which comprises of several layers [44], more attention should be paid to study whether graphene-like monolayer BC3 can be used a new promising electrode material for metal-ion batteries, especially Na/K-ion batteries. Besides, the lattice confinement and mismatch may bring about additional strain on 2D anode materials, which would affect the adsorption and diffusion behaviors of Li/Na/K ions. Therefore, exploring the influence of strain on the electrochemical performances of monolayer BC3 is critical. Thus, in the present study, we systematically investigate the electrochemical performance of graphene-like BC3 monolayer as the anode material for Li/Na/K-ion batteries based on first-principles calculations. According to the calculated structural stability, migration energy barriers, theoretical capacities, and average voltage, we suggest that BC3 monolayer can be utilized as high-performance anodes for Na/K-ion batteries.
Our first-principles calculations are carried out by using the frozen-core projector augmented wave approach [45] as implemented in the Vienna Ab initio Simulation Package (VASP) [46]. The generalized gradient approximation (GGA) in the form proposed by Perdew, Burke, and Ernzerhof (PBE) [47] is used for the exchange-correlation effect. The van der Waals interaction is described by using the semi-empirical correction scheme of Grimme (DFT-D2) [48]. The cutoff energy for the plane wave basis is 500 eV. The Brillouin zone is sampled with a 4×4 × 1 k-points mesh according to Monkhorst-Pack scheme [49]. The convergence criteria for the total energy and the maximum force on each atom are less than 10−5 eV and 0.02 eV/Å, respectively. To minimize the interlayer interactions under the periodic boundary condition, the vacuum spacing is set to be 20.0 Å. In addition, the climbing image nudged elastic band (CI-NEB) method [50] is used to determine the minimum energy diffusion pathways of Li/Na/K atoms and the corresponding energy barriers.
The optimized crystal structure (top and side views) of 3×3 monolayer are illustrated in Fig. 1a, which exhibits a planar configuration similar to that of graphene. In the hexagonal primitive cell highlighted by blue solid line, BC3 contains two B and six C atoms and belongs to P6/mmm space group. The optimized lattice parameters of BC3 are a=b = 5.17 Å, and the calculated bond lengths of C-C and B–C are 1.42 and 1.57 Å, respectively, which agrees well with prior theoretical results [51]. Figs. 1c and d depict the band structure of pristine BC3 monolayer and the corresponding density of state (DOS). It can be seen that BC3 is an indirect semiconductor with the valence band maximum (VBM) located at the Γ point and the conduction band minimum (CBM) lied at the M point. The band gap calculated by using the GGA-PBE and HSE06 functional are 0.66 and 1.81 eV, respectively, which is comparable to previously reported 2D anode materials, such as TMDs, graphitic carbon nitride and phosphorene [52-54]. Accordingly, BC3 monolayer can also be used as an anode despite the absence of metallic feature. The partial DOS shows that the dominant contribution to the CBM is 2p orbitals of the B and C atoms, while the VBM is mainly consist of B-2p and C-2p orbitals. Besides, the electron localization function (ELF), as shown in Fig. S1 (Supporting information), indicates that electron localization occurs around the center of all bonds in BC3 monolayer, revealing the dominance of covalent bonding.

|
Download:
|
| Fig. 1. (a) Top and side views of the optimized structure of BC3 monolayer. (b) The possible adsorption sites for alkali metal atoms that are considered. (c) Electronic band structures of BC3 monolayer at the GGA-PBE and HES06 levels. (d) Total and partial DOSs for BC3 monolayer. Here, the Fermi energy level is scaled to 0 and shown as a black dashed line. | |
Before exploring the potential application of BC3, its structural stability must be examined. On the basis of the finite-displacement method, the phonon band structure of BC3 monolayer is firstly calculated to investigate its dynamic stability. As shown in Fig. 2a, the highest frequency reaches up to 47 THz, demonstrating the robust B–C interaction in the monolayer structure. The acoustic and optic vibration frequencies near the Γ point are well separated from each other. More importantly, there are no any imaginary vibration frequencies along the high symmetric points in the irreducible Brillouin zone, confirming the high stability at 0 K. To further check the thermal stability of monolayer BC3, ab initio molecular-dynamics (AIMD) simulation with canonical ensemble (NVT) is performed at the temperature of 500 K for 10 ps using a 3×3 supercell. As shown in Fig. 2b, we find no obvious structural changes or broken bonds at the end of simulation except for some thermal fluctuations within a small range (< 0.1 eV/atom). This suggests that BC3 monolayer has good thermal stability.

|
Download:
|
| Fig. 2. (a) Phonon band dispersion of the BC3 monolayer. (b) The fluctuation of the total energy during 10 ps AIMD simulation at 500 K. The snapshot of the corresponding structure after the AIMD simulation is given in the inset. (c) Young's modulus and (d) Possion's ratio of the BC3 monolayer as a function of the angle θ. | |
Additionally, by using the finite distortion method, we systematically study the mechanical properties of monolayer BC3, including elastic constants, Young's modulus and Poisson's ratio. The calculated elastic constants in conventional cell are C11 = C22=269.04 N/m, C12=49.73 N/m and C66=109.66 N/m. These obtained values can meet the relationships: C11C22 - C122 > 0, C66 > 0, namely, the Born-Huang criteria are nicely satisfied, implying that the BC3 monolayer is mechanically stable. Based on the above elastic constants, we further calculate the Young's modulus Y(θ) and Poisson's ratio υ(θ) along the in-plane θ, which are expressed as follows:
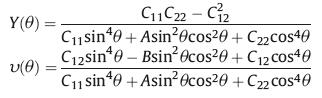
|
where A = (C11C22 - C122)/C66 - 2C12 and B=C11 + C12 - (C11C22 - C122)/C66. The calculated results are depicted in the polar diagrams, as shown in Figs. 2c and d. The diagrams show that both of Young's modulus Y(θ) and Poisson's ratio υ(θ) are remain as constants with changing θ, showing a strong mechanical isotropy. The Young's modulus and Poisson's ratio of the BC3 monolayer are about 259.85 N/m and 0.18, respectively, which are comparable to some common 2D materials such as graphene [55], BN [56] and MoS2 [57]. These results imply that the BC3 monolayer is stable enough for avoiding the curling and might has moderate structural response to external stress.
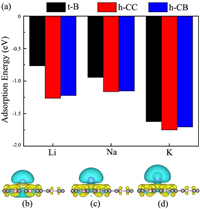
To be a good anode material for alkali-metals ion batteries, it is essential that the BC3 monolayer has relatively strong adsorption energy towards Li/Na/K atoms. In this regard, we therefore study the adsorption behavior of Li/Na/K atoms on a 3×3 BC3 supercell. According to the geometric symmetry of BC3 monolayer, six possible adsorption sites shown in Fig. 1b are considered: h−CC is at the hollow site of hexagon CC ring; h-CB is at the hollow site of hexagon CB ring; b−CC and b-CB are above the midpoints of the C-C bond and C-B bond, respectively; t-C and t-B are located at the top sites of carbon and boron atoms, respectively. To further identify the most favorable adsorption site for these alkali metal atoms, we calculate the corresponding adsorption energy (Ead) by using the following equation,
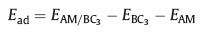
|
where EAM/BC3 and EBC3 are total energies of the BC3 system with and without alkali metal atoms, and EAM is the energy per atom in bulk phase. After full structure relaxation, only three adsorption sites (namely, h−CC, h-CB, and t-B) are stable, and others are transformed into either h−CC or h-CB. For each adsorbed Li/Na/K atoms, as observed from Fig. 3a, the h−CC site is always the most energetically favorable site, followed by the h-CB and t-B sites. At the h−CC site, the heights of the adsorbed Li, Na and K atoms from the monolayer are 1.77, 2.18 and 2.58 Å, respectively, and the corresponding maximum adsorption energies are -1.26, -1.16 and -1.75 eV, respectively. In general, negative adsorption energies means that these Li/Na/K atoms can reside on BC3 monolayer separately rather than forming the metal cluster.
|
Download:
|
| Fig. 3. (a) Adsorption energies of Li/Na/K atoms at the stable t-B, h−CC and h-CB sites of the BC3 monolayer. Differential change density for (b) Li, (c) Na and (d) K adsorbed on BC3 monolayer (isosurface=0.0015 |e|/Å3). Yellow and cyan colors represent charge accumulation and depletion, respectively. | |
To gain deeper insight into the interaction between the alkali metal atoms and BC3 monolayer during the insertion process, we calculate the charge density difference and the results are shown in Figs. 3b-d, with cyan and yellow colors representing △ρ < 0 and △ρ > 0. Because the electronegativities of Li/Na/K atoms are smaller than the C and B, the electron are found to accumulate near the BC3 surface and deplete around the Li/Na/K atoms, that is to say, there are significant charge transfer from the adsorbed atoms to BC3 monolayer. Further, the Bader charge analysis demonstrates that the amounts of transferred electrons are approximately 0.885 |e| for Li, 0.888 |e| for Na and 0.90 |e| for K, donating almost all outermost s electrons. Thus, we can deem that these alkali metal atoms are in the oxidation state and become alkali metal ion.
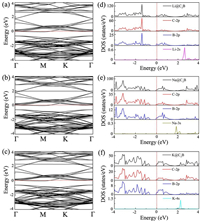
As we known, an anode material has semiconductor characteristic, usually associating with poor electrical conductivity, which is disadvantageous to the efficiency of the battery. However, the electronic properties of semiconductor material might be changed when the alkali metal ions are adsorbed. Consequently, the band structures, total and partial DOSs of Li/Na/K adsorbed BC3 monolayer systems are calculated and plotted in Fig. 4. It can be seen from Figs. 4a-c that all the BC3 systems after adsorption of alkali metals become metallic since their respective Fermi level are shifted into the conduction band. This suggests that the BC3 systems would have sufficient free-electron concentration during the charge/discharge process, ensuring the desired electrical conductivity. Noted that this feature is not sensitive to our chosen functional, and similar conclusion still can be obtained by the HSE06 functional, given in Fig. S2 (Supporting information). Moreover, as indicated in Figs. 4d-f, we find that the s orbitals of Li/Na/K atoms display some clearly discernible peaks in the conduction band, overlapping with the 2p orbitals of C and B. This s-p hybridization interactions in turn push the Fermi level to higher energies, resulting in the semiconductor to metal transition.
|
Download:
|
| Fig. 4. (a-c) Electronic band structures of BC3 monolayer systems after Li/Na/K adsorption. (d-f) Their corresponding total and partial DOSs. Here, the Fermi level is set to 0 and shown as red dashed lines. | |
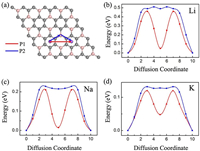
The charge and discharge rate, determined by the mobility of alkali metal atoms, is also critical for the battery's performance compared to electronic conductivity. Therefore, we shift our attention to the Li/Na/K migration process on a 3×3 supercell of BC3 monolayer. The corresponding diffusion energy barriers for different paths are calculated by using the NEB method. Based on our above discussion of the adsorption energy, two possible diffusion paths between the two neighboring most stable adsorption sites are selected, and marked as P1 and P2 in Fig. 5a. In the first path (P1), alkali metal atoms move directly from a h−CC site to another nearest h−CC site via h-CB site; in the second path (P2), they move first to t-B site and then to the neighboring h−CC site. As shown in Figs. 5b-d, all three Li/Na/K atoms prefer to diffuse along P1 since it always has smaller energy barrier than that of P2. This observation is well in accordance with the calculated adsorption energies of Li/Na/K atoms. The lowest diffusion barriers predicted for Li/Na/K atoms are found to be 0.46, 0.21 and 0.12 eV, respectively. These values decreases with increasing atomic radii in the order of Li < Na < K, which can ascribe to the different adsorption height and charge transfer amount that effectively smooths the potential on the BC3 monolayer. Furthermore, we note that Li has the highest diffusion barrier in the all systems, the value is larger than those of graphene (0.28 eV) [58], BP (0.36 eV) [33] and MoS2 (0.25 eV) [59]. To our surprise, the diffusion barriers of Na/K ions are as low as some widely known anode materials, such as graphene (0.13 eV for Na, 0.1 eV for K) [60], BSi3 (0.21 eV for Na, 0.12 eV for K) [61], BP (0.22 eV for Na, 0.16 eV for K) [33], Si3C (0.34 eV for Na, 0.18 eV for K) [62], and C3N (0.03 eV for Na, 0.07 eV for K) [32]. Therefore, BC3 monolayer can be utilized as promising anode materials for Na/K-ion batteries with excellent charge/discharge rate.
|
Download:
|
| Fig. 5. (a) Schematic representation of the possible ion diffusion paths on BC3 monolayer and the corresponding energy barrier profiles for (b) Li, (c) Na and (d) K. | |
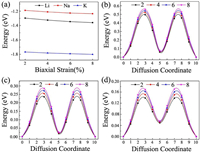
Considering the fact that an electrode material might work in strained states, we also examine the effect of strain on the adsorption and diffusion behaviors of Li/Na/K atoms. The results of adsorption energies and diffusion barriers as a function of strain are depicted in Fig. 6. Here, the in-plane biaxial tensile strains, ranging from 2% to 8% with the 2% increment, are applied on the BC3 monolayer, achieved by enlarging the lattice parameters. It should be noted that these monolayer BC3 structures under different tensile strains are still stable, as indicated by the phonon dispersion curves given in Fig. S3 (Supporting information). Besides, as shown in Fig. S4 (Supporting information), we observe that the band gaps increase in the region of tensile strain. Fig. 6a demonstrates that the values of adsorption energies for Li/Na/K atoms slightly decrease with rising strain, namely, the adsorption become stronger, indicating the continuous enhancement of the interactions between these alkali metal atoms and BC3 monolayer. In detail, under a strain of 8% the adsorption energies decrease to -1.36 eV for Li, -1.24 eV for Na, and -1.79 eV for K. The diffusion barrier profiles of Li/Na/K atoms on the strain engineered BC3 monolayer are given in Figs. 6b-d. In the region of strain, we can see that with an increasing tensile strain all the diffusion barriers also increase, but the increments are quite small. The maximum changes in the diffusion barriers are about 0.10 eV for Li, 0.08 eV for Na, and 0.05 eV for K. Therefore, Na/K still can diffuse easily on the strain engineered BC3 monolayer.
|
Download:
|
| Fig. 6. (a) The adsorption energies of Li, Na, and K on BC3 monolayer vs. biaxial tensile strain. The energy barrier profiles along the lowest energy migration paths under different tensile strains for (b) Li, (c) Na and (d) K. | |
Besides the electronic property and diffusion barrier, the storage capacity and average open-circuit voltage of alkali metal ions are also essential to practical applications in the field of battery technology. Thus, we further investigate the Na/K adsorption behaviors on both sides of the BC3 monolayer and evaluate their respective maximum storage capacities. Here, we adopt a 2×2 supercell of BC3 monolayer, and load the Na/K atoms layer by layer on both sides. For the first adsorption layer, all of the most favorable h−CC sites on both sides of BC3 monolayer are covered by Na/K atoms. For the second layer, we investigate all the possible sites for the successive Na/K atoms and find that both of them favor the h-CB sites. Finally, the t-B sites are occupied by Na/K atoms as the third layer. To compare the adsorption stability, the average adsorption energy (Eave) is calculated layer by layer using the following equation:

|
where EAMnBC3 and EAMn-1BC3 are the total energies of the BC3 monolayer adsorbed with n and n-1 layers, respectively. EAM represents the energy per atom of Na/K atoms in their bulks, and the number "8" corresponds to a total of eight adatoms for each layer. It should be noted that the Na/K atoms could be stably adsorbed on both sides of the BC3 monolayer until the calculated Eave becomes positive, where the highest storage capacity is achieved. After structure optimization, as shown in Fig. S5 (Supporting information), we find that the clustering of Na/K atoms will not occur after structure optimization except for the three-layer adsorbed configuration. Moreover, the average adsorption energies of Na atoms in the first and second layers are calculated to be -0.64 and -0.06 eV per atom, respectively, while the corresponding values for K atoms are -1.03 and -0.14 eV per atom, respectively. These relative negative adsorption energies indicate that our chosen BC3 supercell can accommodate up to 16 Na/K atoms, corresponding to the chemical compositions of Na2BC3 and K2BC3. To check the stability of fully charged anode material (Na2BC3 and K2BC3), we further perform AIMD simulations with the same supercell (2×2) at the temperature of 500 K for 6 ps. As shown in Fig. S6 (Supporting information), the variations of the total energy are quite small during the simulation. The snapshots after 6 ps of simulation show little deviation of Na/K atoms from their equilibrium positions and slight distortion of the BC3 monolayer. These results indicate good thermal stability of the BC3 monolayer at highest capacity.
Thus, the theoretical storage capacity (C) can be evaluated by the following formula:
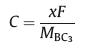
|
where x, F and MBC3 represent the number of electrons involved in the electrochemical process, the Faraday constant (26.8 mAh/g), and the molecular mass of BC3, respectively. The maximum theoretical storage capacity is estimated to be 1653 mAh/g when BC3 monolayer acts as anodes of Na/K-ion batteries. The high storage capacity in the BC3 monolayer mainly originates from its multilayered adsorption ability. These values predicted in the present study are among the highest ones in the experimental and theoretical reported anode materials, such as C3N (1072 mAh/g for Na and K) [32], Si3C (1115 mAh/g for Na, 836 mAh/g for K) [62] and B2S (2245 mAh/g for Na, 1167 mAh/g for K) [63], implying that BC3 monolayer possesses ultra-high Na/K storage capacity.
To further determine the electrode property, the open-circuit voltage (OCV) during the Na/K loading process is studied. In the event of neglecting the effects of volume and entropy, the average voltage of AMxBC3 in the concentration range of x1 < x < x2 can be estimated using

|
where EAMx2BC3 and EAMx1BC3 are the total energies of the AMxBC3 compound at two adjacent low-energy concentrations x2 and x1. e represents the electronic charge, and EAM represents the energy per atom of Na/K atoms in their bulks. Noted that we choose five values for the concentration x, which is 0.25, 0.50, 1.00, 1.50 and 2.00. For each adsorption concentration, we compare the energies of different structures, and adopt the one with the lowest energy to calculate the voltage. The concentration-dependent OCV profiles for Na/K ions are shown in Fig. 7. It can be clearly see that the OCVs of Na/K ions exhibit a decreasing trend as the concentration x increase. The calculated OCVs for NaxBC3 and KxBC3 are in the range of 0.89−0.07 V and 1.29−0.32 V, which are always positive during the entire adsorption process. This implies that the half-cell reactions can proceed spontaneously until their respective final conditions (Na2BC3 and K2BC3), resulting in a fully reversible capacity of 1653 mAh/g. Moreover, the corresponding average voltages are 0.38 and 0.66 V. Fortunately, both of them are within the desired potential ranges, ensuring to produce high cell voltages. These results suggest that BC3 monolayer can be a promising anode material for Na/K-ion batteries.

|
Download:
|
| Fig. 7. Calculated open-circuit voltage of the BC3 anode for Na/K adsorption at different concentrations. | |
In conclusion, based on first-principles calculations, we systematically investigate the potential of graphene-like BC3 monolayer as electrode materials for Li/Na/K-ion batteries. Our results show that BC3 monolayer is a small band gap semiconductor with high structural stabilities. The Li/Na/K atoms prefer to at the h−CC site of the BC3 monolayer with adequate negative adsorption energies and charge transfer. It is also found that the BC3 monolayer becomes metallic after adsorbing Li/Na/K, thus enhancing the electronic conductivity. Moreover, the diffusion energy barriers are estimated to be 0.46 eV for Li, 0.21 eV for Na, and 0.12 eV for K, indicating that BC3 monolayer would has high charge/discharge rates for Na/K-ion batteries. Besides, our further calculations show that the adsorption and diffusion performances of Li/Na/K atoms are almost unaffected by the tensile strains. More importantly, the maximum theoretical storage capacities for Na/K-ion batteries are as high as 1653 mAh/g, and the corresponding average open circuit voltages are 0.38 and 0.66V, respectively. Combining those advanced features, it is expected that the BC3 monolayer could be utilized as an excellent anode material for Na/K-ion batteries in the near future.
Declaration of competing interestThe authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
AcknowledgmentsThis work was partially supported by the National Natural Science Foundation of China (No. 21503149), by the Program for Innovative Research Teamin University of Tianjin (No. TD13-5074), by the Project of Hubei University of Arts and Science (No. 2020kypyfy015) and Hubei Superior and Distinctive Discipline Group of "Mechatronics and Automobiles" (No. XKQ2020021).
Appendix A. Supplementary dataSupplementary material related to this article can be found, in the online version, at doi:https://doi.org/10.1016/j.cclet.2020.07.016.
| [1] |
E. Pomerantseva, Y. Gogotsi, Nat. Energy 2 (2017) 17089. DOI:10.1038/nenergy.2017.89 |
| [2] |
Y. Dong, S. Li, S. Hong, et al., Chin. Chem. Lett. 31 (2020) 635-642. DOI:10.1016/j.cclet.2019.08.021 |
| [3] |
R. Rojaee, R. Shahbazian-Yassar, ACS Nano 14 (2020) 2628-2658. DOI:10.1021/acsnano.9b08396 |
| [4] |
G. Harper, R. Sommerville, E. Kendrick, et al., Nature 575 (2019) 75-86. DOI:10.1038/s41586-019-1682-5 |
| [5] |
F. Zhao, X. Zhao, B. Peng, et al., Chin. Chem. Lett. 29 (2018) 1692-1697. DOI:10.1016/j.cclet.2017.12.015 |
| [6] |
J.B. Goodenough, K.S. Park, J. Am. Chem. Soc. 135 (2013) 1167-1176. DOI:10.1021/ja3091438 |
| [7] |
X. Kong, J. Zhang, J. Huang, et al., Chin. Chem. Lett. 30 (2019) 771-774. DOI:10.1016/j.cclet.2018.10.006 |
| [8] |
D. Larcher, J.M. Tarascon, Nat. Chem. 7 (2015) 19-29. DOI:10.1038/nchem.2085 |
| [9] |
H. Tan, Y. Feng, X. Rui, et al., Small Methods 4 (2020) 1900563. DOI:10.1002/smtd.201900563 |
| [10] |
Y.H. Zhu, X. Yang, D. Bao, et al., Joule 2 (2018) 736-746. DOI:10.1016/j.joule.2018.01.010 |
| [11] |
Y. Wu, H.B. Huang, Y. Feng, et al., Adv. Mater. 31 (2019) 1901414. DOI:10.1002/adma.201901414 |
| [12] |
Y.X. Wang, W.H. Lai, Y.X. Wang, et al., Angew. Chem. Int. Ed. 58 (2019) 18324-18337. DOI:10.1002/anie.201902552 |
| [13] |
J. Xu, W. Wei, X. Zhang, et al., Chin. Chem. Lett. 30 (2019) 1341-1345. DOI:10.1016/j.cclet.2019.03.005 |
| [14] |
Z. Yan, Q.W. Yang, Q. Wang, et al., Chin. Chem. Lett. 31 (2020) 583-588. DOI:10.1016/j.cclet.2019.11.002 |
| [15] |
C. Vaalma, D. Buchholz, M. Weil, et al., Nat. Rev. Mater. 3 (2018) 18013. DOI:10.1038/natrevmats.2018.13 |
| [16] |
B. Xu, S. Qi, F. Li, et al., Chin. Chem. Lett. 31 (2020) 217-222. DOI:10.1016/j.cclet.2019.10.009 |
| [17] |
Y. Fang, X. Li, J. Li, et al., J. Mater. Chem. A 7 (2019) 25691-25711. DOI:10.1039/C9TA10487A |
| [18] |
J. Wang, M. Zhang, J. Meng, et al., RSC Adv. 7 (2017) 24446-24452. DOI:10.1039/C7RA01723E |
| [19] |
Y. Liu, X. Duan, Y. Huang, et al., Chem. Soc. Rev. 47 (2018) 6388-6409. DOI:10.1039/C8CS00318A |
| [20] |
J. Wang, X. Yang, J. Cao, et al., Comput. Mater. Sci. 150 (2018) 432-438. DOI:10.1016/j.commatsci.2018.04.049 |
| [21] |
J. Pang, R.G. Mendes, A. Bachmatiuk, et al., Chem. Soc. Rev. 48 (2019) 72-133. DOI:10.1039/C8CS00324F |
| [22] |
J. Mei, T. Liao, L. Kou, et al., Adv. Mater. 29 (2017) 1700176. DOI:10.1002/adma.201700176 |
| [23] |
Y. Shen, J. Liu, X. Li, et al., ACS Appl. Mater. Interfaces 11 (2019) 35661-35666. DOI:10.1021/acsami.9b09223 |
| [24] |
A. Samad, A. Shafique, Y.H. Shin, Nanotechnology 28 (2017) 175401. DOI:10.1088/1361-6528/aa6536 |
| [25] |
J. Zhu, H.N. Alshareef, U. Schwingenschlögl, Appl. Phys. Lett. 111 (2017) 043903. DOI:10.1063/1.4985694 |
| [26] |
Y. Yu, J. Zhou, Z. Sun, Nanoscale 11 (2019) 23092-23104. DOI:10.1039/C9NR08217D |
| [27] |
Y. Wang, M. Zhou, L.C. Xu, et al., J. Power Sources 451 (2020) 227791. DOI:10.1016/j.jpowsour.2020.227791 |
| [28] |
Q. Meng, A. Hu, C. Zhi, et al., Phys. Chem. Chem. Phys. 19 (2017) 29106-29113. DOI:10.1039/C7CP06171D |
| [29] |
H. Wang, M. Wu, X. Lei, et al., Nano Energy 49 (2018) 67-76. DOI:10.1016/j.nanoen.2018.04.038 |
| [30] |
S. Qi, F. Li, J. Wang, et al., Carbon 141 (2019) 444-450. DOI:10.1016/j.carbon.2018.09.031 |
| [31] |
J. Xu, J. Mahmood, Y. Dou, et al., Adv. Mater. 29 (2017) 1702007. DOI:10.1002/adma.201702007 |
| [32] |
P. Bhauriyal, A. Mahata, B. Pathak, J. Phys. Chem. C 122 (2018) 2481-2489. DOI:10.1021/acs.jpcc.7b09433 |
| [33] |
H.R. Jiang, W. Shyy, M. Liu, et al., J. Mater. Chem. A 5 (2017) 672-679. DOI:10.1039/C6TA09264K |
| [34] |
Y. Dong, W. Wei, X. Lv, et al., Appl. Surf. Sci. 479 (2019) 519-524. DOI:10.1016/j.apsusc.2019.02.123 |
| [35] |
Z. Zhao, T. Yu, S. Zhang, et al., J. Mater. Chem. A 7 (2019) 405-411. DOI:10.1039/C8TA09155B |
| [36] |
P. Li, Z. Li, J. Yang, J. Phys. Chem. Lett. 9 (2018) 4852-4856. DOI:10.1021/acs.jpclett.8b02035 |
| [37] |
H. Tanaka, Y. Kawamata, H. Simizu, et al., Solid State Commun. 136 (2005) 22-25. DOI:10.1016/j.ssc.2005.06.025 |
| [38] |
Aghaei S.Mehdi, M.M. Monshi, I. Torres, et al., Appl. Surf. Sci. 427 (2018) 326-333. DOI:10.1016/j.apsusc.2017.08.048 |
| [39] |
H. Zhang, Y. Liao, G. Yang, et al., ACS Omega 3 (2018) 10517-10525. DOI:10.1021/acsomega.8b01998 |
| [40] |
C. Zhang, Y. Jiao, T. He, et al., J. Phys. Chem. Lett. 9 (2018) 858-862. DOI:10.1021/acs.jpclett.7b03449 |
| [41] |
J. Song, Z. Xu, X. He, et al., Phys. Chem. Chem. Phys. 21 (2019) 12977-12985. DOI:10.1039/C9CP01943J |
| [42] |
S. Aydin, M. Şimşek, Int.J.Hydrogen Energy 44 (2019) 7354-7370. DOI:10.1016/j.ijhydene.2019.01.222 |
| [43] |
B. Mortazavi, M. Shahrokhi, M. Raeisi, et al., Carbon 149 (2019) 733-742. DOI:10.1016/j.carbon.2019.04.084 |
| [44] |
R.P. Joshi, B. Ozdemir, V. Barone, et al., J. Phys. Chem. Lett. 6 (2015) 2728-2732. DOI:10.1021/acs.jpclett.5b01110 |
| [45] |
P.E. Blöchl, Phys. Rev. B 50 (1994) 17953. DOI:10.1103/PhysRevB.50.17953 |
| [46] |
G. Kresse, J. Furthmüller, Phys. Rev. B 54 (1996) 11169. DOI:10.1103/PhysRevB.54.11169 |
| [47] |
J.P. Perdew, K. Burke, M. Ernzerhof, Phys. Rev. Lett. 77 (1996) 3865. DOI:10.1103/PhysRevLett.77.3865 |
| [48] |
S. Grimme, J. Comput. Chem. 27 (2006) 1787-1799. DOI:10.1002/jcc.20495 |
| [49] |
H.J. Monkhorst, J.D. Pack, Phys. Rev. B 13 (1976) 5188. DOI:10.1103/PhysRevB.13.5188 |
| [50] |
G. Henkelman, B.P. Uberuaga, H. Jonsson, J. Chem. Phys. 113 (2000) 9901-9904. DOI:10.1063/1.1329672 |
| [51] |
Y. Tang, H. Chai, H. Zhang, et al., Phys. Chem. Chem. Phys. 20 (2018) 14040-14052. DOI:10.1039/C8CP00772A |
| [52] |
J. Wang, Z. Guan, J. Huang, et al., J. Mater. Chem. A 2 (2014) 7960-7966. DOI:10.1039/C4TA00275J |
| [53] |
J. Guan, Z. Zhu, D. Tománek, Phys. Rev. Lett. 113 (2014) 046804. DOI:10.1103/PhysRevLett.113.046804 |
| [54] |
J. Wang, X. Li, Y. You, et al., Nanotechnology 29 (2018) 365401. DOI:10.1088/1361-6528/aace20 |
| [55] |
C. Lee, X. Wei, J.W. Kysar, et al., Science 321 (2008) 385-388. DOI:10.1126/science.1157996 |
| [56] |
L. Song, L. Ci, H. Lu, et al., Nano Lett. 10 (2010) 3209-3215. DOI:10.1021/nl1022139 |
| [57] |
R.C. Cooper, C. Lee, C.A. Marianetti, et al., Phys. Rev. B 87 (2013) 035423. DOI:10.1103/PhysRevB.87.035423 |
| [58] |
L. Zhou, Z.F. Hou, B. Gao, et al., J. Mater. Chem. A Mater. Energy Sustain. 4 (2016) 13407-13413. DOI:10.1039/C6TA04350J |
| [59] |
H. Shu, F. Li, C. Hu, et al., Nanoscale 8 (2016) 2918-2926. DOI:10.1039/C5NR07909H |
| [60] |
S. Gong, Q. Wang, J. Phys. Chem. C 121 (2017) 24418-24424. DOI:10.1021/acs.jpcc.7b07583 |
| [61] |
J. Zhu, A.N. Gandi, U. Schwingenschlögl, Adv. Theory Simul. 1 (2018) 1800017. DOI:10.1002/adts.201800017 |
| [62] |
Y. Wang, Y. Li, J. Mater. Chem. A 8 (2020) 4274-4282. DOI:10.1039/C9TA11589G |
| [63] |
S. Lei, X. Chen, B. Xiao, et al., ACS Appl. Mater. Interfaces 11 (2019) 28830-28840. DOI:10.1021/acsami.9b07219 |
 2021, Vol. 32
2021, Vol. 32 

