b State Key Laboratory of Precision Spectroscopy, School of Physics and Materials Science, East China Normal University, Shanghai 200062, China ;
c Center for Organic Photonics and Electronics Research(OPERA), Kyushu University, Fukuoka 819-0395, Japan
Metal-free, thermally activated delayed fluorescence (TADF) materials are characterized by luminescent molecules or complexes with small energy gap (ΔEST) between the lowest singlet (S1) and triplet (T1) excited states [1-4]. They can upconvert from the T1 to S1 by absorbing environmental thermal energy and then radiatively decay from the S1. TADF emitters can be employed in OLEDs to convert both singlet and triplet excitons into light with a theoretical yield up to 100% [5-17]. Because OLEDs containing TADF emitters can be up to four times more efficient than OLEDs containing fluorescent molecules, and cheaper than OLEDs containing noble metal-based phosphor, they have garnered considerable research attention in recent years [18-28].
Small ΔEST value is the key to realizing an efficient TADF. We now know that two conditions must be met to ensure a small ΔEST: The first is a small exchange integral for the S1 transition, which is roughly proportional to the degree of overlap between the initial and final state orbitals and is generally realized by an intermolecular or intramolecular charge-transfer (CT) [5-13]; the second is that the locally excited triplet state (3LE) be close to (or even exceed) the 3CT (Fig. 1) [15, 18, 21]. If theoretical calculations can accurately predict the transition energies of CT molecules, the time and cost of developing new TADF materials can be substantially reduced.

|
Download:
|
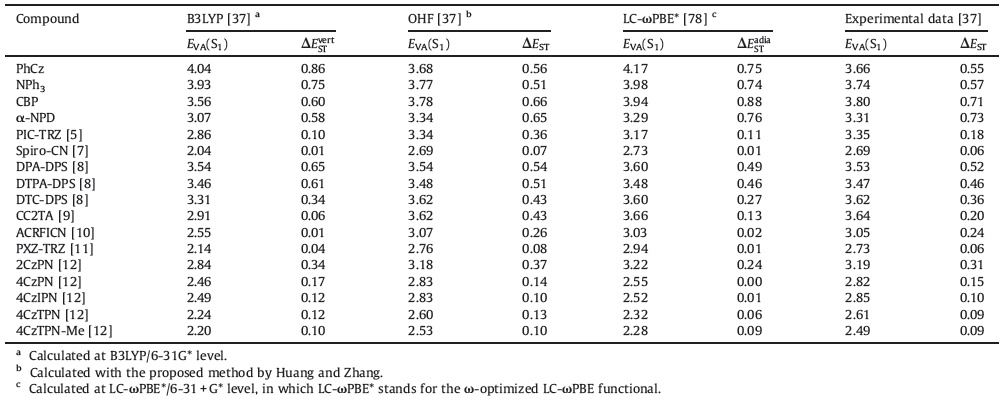
| Figure 1. Singlet and triplet energy levels of ICT molecules. The T1 of molecule A is an LE state, while that of molecule B is a CT state. The singlet-triplet splitting of a LE transition is generally larger than that of a CT transition. | |
Owing to its ability to balance accuracy and efficiency, the linear response time-dependent density functional theory (LR-TDDFT), which was developed based on density functional theory, has become the most widely used method for theoretical interpretation of excited-state electron structure and dynamics for medium to large molecular systems [29-31]. The resolution of the LR-TDDFT equations performed at optimized ground- and excited-state geometries can reproduce the vertical absorption and emission energies, as well as the adiabatic energy (approximate to the zero-zero transition energy) under the Franck-Condon principle (Fig. 2) [32-34]. However, the TDDFT results for CT states are highly dependent on the selected exchange-correlation (XC) - especially the Hartree-Fock (HF) percentage contained therein - when hybrid-functionals are used [31, 35-37]. Consequently, the transition energies of different molecules must be calculated by using different XC-functionals. Moreover, when the singlet-triplet pairs of low-lying excited states are crossed in a TADF molecule, as shown in Fig. 1a, the transitions of S1 and T1 involving different orbitals must also be reproduced by different XC-functionals [37]. The challenge for theoretical chemists, to this effect, is to secure a systemic and universal strategy for the selection or correction of XC-functionals to facilitate accurate prediction of the transition energies of various TADF (and even CT) systems.

|
Download:
|
| Figure 2. (a) Illustration of the Franck-Condon principle. Electronic transitions are from level to level. The vertical lines (EVA, EVE and E0-0) represent experimental values. (b) Theoretically computed energies of EVA, EVE, and EAD. The zero-point vibrational energy offsets the energy difference between the potential well and the vibrational level. Reproduced with permission from ref [37]. Copyright 2013 American Chemical Society. | |
This brief review begins by introducing the theoretical and experimental error sources in the studies of transition energies of CT-type TADF molecules, then goes on to summarize current efforts to overcome these problems.
2. Error sources in theoretical prediction of TADF molecule transition energy 2.1. Drawbacks to existing theoretical modelsThe TDDFT scheme derived from linear response formalism is necessary for solving any non-Hermitian eigenvalue equation [31, 35, 36]:
| $\left[ {\matrix{ A & B \cr {{B^ * }} & {{A^ * }} \cr } } \right]\left[ {\matrix{ X \cr Y \cr } } \right] = \omega \left[ {\matrix{ 1 & 0 \cr 0 & { - 1} \cr } } \right]\left[ {\matrix{ X \cr Y \cr } } \right]$ | (1) |
where A and B are the Hamiltonian matrix elements of the single (de)excitation determinants, X and Y are the single (de)excitation amplitudes, and ω is the excitation energy. When a hybrid- functional is used, matrices A and B can be expressed in Mulliken notation as follows:
| $\begin{align} & {{A}_{ia,jb}}={{\delta }_{ij}}{{\delta }_{ab}}\left( {{\varepsilon }_{a}}-{{\varepsilon }_{i}} \right)+\left( ia\left| jb \right. \right)- \\ & {{C}_{HF}}\left( ij\left| ab \right. \right)+\left( 1-{{C}_{HF}} \right)\left( ia\left| {{f}_{XC}} \right|jb \right) \\ \end{align}$ | (2) |
| ${{B}_{ia,jb}}=\left( ia\left| bj \right. \right)-{{C}_{HF}}\left( ib\left| aj \right. \right)+\left( 1-{{C}_{HF}} \right)\left( ia\left| {{f}_{XC}} \right|bj \right)$ | (3) |
where ij are used for ground state occupied orbitals, a, b for vitual orbitals, δ is the Kronecker delta, ε is the orbital energy, fxc is the exchange-correlation kernel, and CHF is the percentage of Hatree- Fock exchange in the hybrid functional.
For a long-range CT transition, the overlap between the original and final orbitals decreases to zero. Thus, A and B can be simplified to:
| ${{A}_{ia,jb}}={{\delta }_{ij}}{{\delta }_{ab}}\left( {{\varepsilon }_{a}}-{{\varepsilon }_{i}} \right)-{{C}_{HF}}\left( ij\left| ab \right. \right)$ | (4) |
| ${{B}_{ia,jb}}=0$ | (5) |
The neglect of matrix B for a CT transition is well known as the Tamm-Dancoff Approximation (TDA) [38, 39]. The first term in the expression of matrix A is the energy difference between the virtual and occupied orbitals, while the second is a Coulomb-like term that is essential in reproducing the 1/R fall-off condition that results from electrostatic attraction between the separated hole (orbitals that lose electrons) and electron (orbitals that obtain electrons). The absence of a selection rule on CHF generally prevents exact prediction of the transition energies. Additionally, the optimized geometries in excited states are generally more sensitive than those in ground state to CHF due to the relatively flatter potential energy surfaces in the excited states [33], which makes predicting the transition energies (e.g., Eve and EAD) even more difficult on the basis of the excited state geometries.
To theoretically interpret the excitation process in a given environment, the solvation model must be introduced to the TDDFT calculation. Recent studies have indicated that the solvation of some TADF molecules cannot be satisfactorily reproduced by employing a polarizable continuum model (PCM) [16, 40-42], while the effects of other solvation models such as CPCM [43, 44] SS [45, 46] COSMO [47], SCIPCM [48], SMD [49], or SM8 [50] remain unknown. In addition to the solvation model used, the size of the basis set [37, 40, 51] and weak interaction [40] also affect the TDDFT results (though the influence of either is relatively small).
2.2. Issues in spectrum analysisExperimental spectroscopic data is the primary evidence utilized to evaluate the reliability of calculated transition energies. Although the Eva(S1) , Eve(S1) , E0-0(S1) , E0-0(T1) , and ΔEST of TADF materials can be determined based on their adsorption, fluorescence, and low-temperature phosphorescence spectra in theory, the complicated experimental spectra do not readily provide reliable data - as discussed above, this makes developing a theoretical approach for the prediction of transition energies quite difficult.
The adsorption and emission spectra of organic molecules in gaseous state are narrow and sharp. Consequently, they allow level-to-level transitions to be easily identified (Fig. 3). In medium polar solvents (e.g. toluene) or organic semiconductor films, the spectrum of an LE transition may retain well-defined vibronic structures (e.g., anthracene and carbazole) while that of a CT transition is always broad and featureless (Fig. 3) [52]. According to the Franck-Condon principle, the maxima of CT adsorption and emission correspond to EVA and Eve, respectively, while the average of EVA and EVE or the crossing point between absorption and emission (normalized to the same height) corresponds approximately to the E0-0 of the CT transition [53, 54]. A CT transition with slight overlap of the involved orbitals exhibits a weak absorption band which is easily covered by other higher transitions (e.g., S2), making it difficult to determine Eva(S1). An assumed mirror-image relationship between the first absorption band and the fluorescence spectrum (mirror-image rule) was recently used to determine Eva(S1) from easily identified Eve(S1) [37], however, the premise of this rule is a small structure variation between the ground and excited state geometries, which cannot be guaranteed in CT transitions [55].
|
Download:
|
| Figure 3. Schematic representation of the absorption and fluorescence spectra of an ICT molecule. Smooth curves represent the spectra recorded in liquids or solids, while narrow lines in the spectra of dilute gases correspond to the energy diagram illustrated in Fig. 2a. | |
For the emission spectrum of a CT transition in medium polar medium, the intersection point (onset) between the base line and the tangent line of the high energy side (passing through the halfheight point) corresponds closely to the 0-0 energy (Fig. 3) [56]. In high polar solvents, however, there may be strong red-shift of the emission spectrum weakens the correspondence between the emission onset and the 0-0 energy.
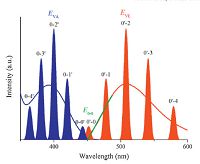
The determination of E0-0(T1) from low-temperature phosphorescence spectra is a bit more complicated. Theoretically, similar to fluorescence spectra, the onset of a broad emission band corresponds to the E0-0 of a 3CT transition while the highest energy peak of a vibrational emission band corresponds to the E0-0 of a 3LE transition. However, different to the room temperature fluorescence which is mainly attributed to the radiative S1→S0 transition, T2→S0 transition as well as the TADF can contribute to the delayed spectra measured at low temperatures (Fig. 4a). Rigid and low-temperature (usually 77 K) environments slow the T2→T1 internal conversion but cannot inhibit the T1→T2 or T1→S1 upconversion [12, 15, 56]. To liminate the influence of delayed fluorescence, the testing temperature for any emitters with very small ΔEST (<0.1 eV) should be extra low [12, 15, 56]. Comparison among the fluorescence and the phosphorescence spectra of molecular fragments enables us to judge the nature of the low temperature delayed spectra (Fig. 4b) [8, 15], but even so, it is difficult to reliably estimate the E0-0(T1) of certain molecules from the spectra due to their low phosphorescence yield at low temperatures [16, 57].

|
Download:
|
| Figure 4. (a) Time-resolved emission spectra of PPZ-DPO doped into a wide-band-gap host at 10 K, measured by a streak camera. Phosphorescence from two triplet excited states can be distinguished by the spectra. (b) Phosphorescence spectra of PPZ-DPO in doped film at 10 K (delayed 1 ms) and in toluene at 77 K (delayed 10 ms). The phosphorescence spectrum in toluene has been demonstrated to arise from a 3LE state located mostly on the 5-phenyl-5, 10-dihydrophenazine (PPZ) fragment. Although the phosphorescence spectrum of PPZ-DPO in the film has no vibronic structure, the profile of its phosphorescence spectrum is more similar to that of PPZ than its fluorescence spectrum, indicating a LE nature for the T1 of PPZ-DPO in the film. Reproduced with permission from ref [15]. Copyright 2014 Nature Publication Group. | |
Estimating ΔEST by a different approach than emission spectra is necessary. In 2012, Gousih et al. [6] deduced the following equation for the reverse intersystem crossing (RISC) rate constant (kRISC) of TADF molecules:
| ${{k}_{PISC}}=\left( \frac{{{k}_{p}}{{k}_{d}}}{{{k}_{ISC}}} \right)\left( \frac{{{\phi }_{d}}}{{{\phi }_{p}}} \right)$ | (6) |
where kp and kd are the rate constants of the prompt and delayed fluorescence components, respectively, kISC is the intersystem crossing (ISC) rate constant from S1 to T1, and φp and φd are the photoluminescence quantum efficiencies of the prompt and delayed components. Because ln(kRISC) is inversely proportional to ΔEST/T (where T is temperature, ) ΔEST can be obtained through linear fitting of ln(kRISC) with a series of T.
Meanwhile, Nakagawa et al. [7] suggested estimating ΔEST using a Berberan-Santos plot from the following equation:
| $\ln =\left[ \frac{\phi }{{{\phi }_{d}}}-\left( \frac{1}{{{\phi }_{T}}}-1 \right) \right]=\ln \left( \frac{{{k}_{p}}+{{k}_{nr}}}{{{k}_{RISC}}} \right)+\frac{\Delta {{E}_{ST}}}{RT}$ | (7) |
where φT is the triplet formation efficiency, kp is the phosphorescence rate constant, knr is the non-radiative rate constant from T1, and R is the ideal gas constant.
To estimate ΔEST using Eq. (6) or (7) , it is necessary to examine the quantum yields and emission decay characteristics of the samples at various temperatures between 140 K and 300 K, which is high cost and time-consuming. Very recently, Zhang et al. [15, 16] established a simple method for estimating the ΔEST of a TADF emitter at room temperature via the following approximate relationship:
| ${{k}_{d}}=\frac{1}{3}\left[ {{k}_{p}}\cdot \exp \left( -\frac{\Delta {{E}_{ST}}}{RT} \right) \right]$ | (8) |
This equation is simplified from a more general expression for the temperature dependence of the lifetimes of two excited states in thermal equilibrium when the gap between these two states ranges from 0.05 eV to 0.30 eV. According to this equation, if a molecule has a TADF lifetime as long as hundreds of microseconds, its ΔEST can be hardly lower than 0.1 eV.
3. Steps toward theoretical prediction of TADF 3.1. Traditional hybrid density functional methodsThe properties of TADF materials are mainly determined by ΔEST as well as the energy and oscillator strength of the S1→S0 transition [8, 12, 15]. As mentioned above, choosing the right functional to calculate these parameters within TDDFT remains a problem. The most popular functionals used in TDDFT are generally hybrids (e.g., B3LYP [58], PBE0 [59], and M06-2X [60]) that perform well in terms of ground state calculations. Range- separated functionals (e.g., CAM-B3LYP [61], LC-GGA [62, 63] and vB97X-D [64]) in which the Coulomb operator is divided into short-range and long-range parts are also good candidates. In comparison with the theoretical energy of an LE transition, that of a CT transition is more sensitive to the Hartree-Fock percentage (HF%) in the XC functional of TDDFT. Previous studies have indicated that traditional hybrid functionals with low HF% such as B3LYP (20%HF) and PBE0 (25%HF) inherently underestimate the vertical transition energies of TADF molecules (Fig. 5) [12, 65-70] with few exceptions [51] (Table 1). By contrast, high HF% in the long-range parts of CAM-B3LYP (19%HF in short-range and 65%HF in long-range) and ωB97X-D (22%HF in short-range and 100%HF in long-range) generally leads to excess transition energy [12, 41, 71, 72] although quite accurate results can be obtained sometimes via CAM-B3LYP [73, 74].

|
Download:
|
| Figure 5. Molecular structures of phenylcarbazole, triphenylamine, and various ICT compounds based on carbazole or diphenylamine donor. | |
Very recently, Moral et al. [40] found that the double-hybrid functional B2GP-PLYP [75] performs well in calculating EVA for several TADF molecules. For instance, the absolute difference between the theoretical and experimental values of EVA(S1) for ACRFLCN and 2CzPN are both smaller than 0.1 eV. The cost of a double-hybrid functional is typically one order of magnitude higher than that of a traditional hybrid functional, however, which limits the application of this method to further studies on TADF [76, 77].
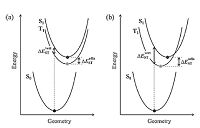
There are two main ways to calculate ΔEST: Taking the difference between EVA(S1) and EVA(T1) (ΔESTvert), or taking the energy difference between the optimized S1 and T1 states ΔESTadia [32, 34, 41]. As illustrated by the Franck-Condon principle energy diagram shown in Fig. 6, the first method is theoretically reliable only when S1 and T1 have nearly identical equilibrium geometries, i.e., the orbitals involved in S1 and T1 transitions are almost the same. Conversely, if the T1 of a CT molecule is in a locally excited state, the first method tends to overestimate ΔEST because the relaxation energy of a CT state is always larger than that of a LE state (Fig. 6b). The ΔESTvert calculated at the B3LYP level sometimes shows good agreement with the experimental ΔEST [8, 12, 41, 65] (Table 1) owing to an undervaluation of the S1 (CT) transition energies and an error cancellation. Although the second method seems more reasonable in theory, especially when the zero-point energy is considered, the selection of correct XC-fuctionals for S1 and T1 geometry optimization is problematic. For instance, the ΔESTadia of DTC-DPS, 2CzPN, 4CzIPN, and 4CzTPN calculated at the B3LYP level are all negative values representing a qualitative mistake [78].
|
Download:
|
| Figure 6. Potential energy surfaces of TADF molecules. The T1 surface in (a) corresponds to a 3CT state while that in (b) corresponds to a 3LE state. | |
3.2. Semiempirical descriptor-based optimal Hartree-Fock percentage (OHF) methods
There is most likely no exact and universal exchange- correlation kernel for predicting the energies of all transitions. In 2008, in effort to warn against possible TDDFT failures, Peach et al. adopted a descriptor ∧ to depict the degree of overlap between the initial and final orbitals in a transition and assess the suitability of B3LYP, PBE0, and CAM-B3LYP for transitions with different ∧ values [79]. A number of descriptors were then designed to depict the characteristics of various CT transitions [8084]. In 2013, Huang and Zhang et al. introduced the descriptor method to the TDDFT prediction of TADF and significantly improved the computational accuracy [37].
Huang and Zhang et al. calculated the EVA(S1) of all TADF molecules (Fig. 5) reported at that time via several different XC- functionals to find that the calculated EVA(S1) strongly depends on the HF%, almost regardless of the difference in the expression of said XC functionals. The continuous and monotonic dependence of Eva(S1) on HF% allows for an optimal HF% (OHF) in the EVA(S1) calculation (Fig. 7a). There appears to be a highly linear correlation between OHF and CT amount q (OHF = 42q), where q is defined as the quantity of the charge on un-overlapped HOMO or LUMO (Fig. 7b). Eva(S1) and Eve(S1), as well as the E0-0(S1) that approximates to their average, can be predicted according to this empirical correlation. Because it is not possible to judge the nature of T1 based on configuration interaction description, the EVA(T1) values points corresponding to a CT or LE excited state were determined according to the change in EVA(S1)-EVA(T1) compared to HF% (Fig. 7a). Two semi-empirical formulas were then derived to calculate E0-0(3CT) from E0-0(1CT), EVA(1CT), and EVA(3CT), and to calculate E0-0(3LE) from EVA(3LE). After calculating E0-0(S1)and E0-0(T1) independently, the ΔEST of various TADF molecules were accurately reproduced (Table 1).

|
Download:
|
| Figure 7. (a) Dependence of EVA(S1) and EVA(T1) of DTC-DPS and PhCz on HF% in TD-DFT functionals. (b) Dependence of the optimal HF% for calculating EVA(S1) on the CT amount calculated at the B3LYP/6-31G* level based on S0 geometry. The structures of the molecules in this figure are shown in Fig. 5. Reproduced with permission from ref [37]. Copyright 2013 American Chemical Society. | |
|
|
Table 1 Comparison of calculated EVA(S1) and ΔEST with experimental data. |
The corrected TDDFT method on the basis of OHF has been applied to the molecular design for TADF materials intended for OLED application. Highly efficient blue TADF emitters having extremely small ΔEST [15] and efficient red TADF emitters having both high transition rate (large f) and small ΔEST [16] have been successfully developed with the assistance of this method, in fact. Reducing the empirical content as well as number of processing steps would make the OHF method even more attractive.
In the last couple of years, more and more descriptors have been introduced into studies on TADF. For instance, Moral etal. observed a dependence of the experimental ΔEST on the calculated electron- hole distance Δr(NTO), an index defined as the distance between the centroids of the highest occupied and the lowest unoccupied natural transition orbitals (NTOs) [40]. Penfold pointed out that the traditional descriptor ∧ (marked O in his article) does not consider the (de)localization and spatial extent of related orbitals in a molecule and therefore fails to accurately indicate ΔEST; he suggested additionally using the HOMO-LUMO gap (εgap) to describe the orbital (de)localization degree and proposed a new descriptor ∧⋅εgap accordingly. The dependence of the experimental ΔEST on ∧⋅εgap has proven a better indicator than that on A [85]. Chen et al. established the following relationship regarding ΔEST:
| $\Delta {{E}_{ST}}\propto \frac{\Lambda _{S}^{2}}{\Delta {{r}_{S}}}+\frac{\Lambda _{T}^{2}}{\Delta {{r}_{T}}}$ | (9) |
where ∧S and ∧T are the overlap integral between the dominating orbital pairs of S1 and T1 transitions, while ΔrS and ΔrT are the corresponding transition distances [86]. Accordingly, localized T1 state may lead to large ΔEST. Like q, these recently proposed descriptors do have potential application terms of the proper selection of XC functionals for modeling ICT molecules.
3.3. Optimally tuned range-separated density functionalThe optimal "tuning" approach based on the range-separated (RS) density functionals has attracted increasing research attention as it has proven to efficiently provide reliable prediction for the band gaps and charge-transfer excitation energies of organic molecular systems [87-94].The "non-empirical" nature of this tuning method lies in the way that the range-separated parameter v is determined not by fitting a large number of experimental data, but by satisfying the Koopmans theory to the maximum extent, i.e. ensuring the negative HOMO energy equals the vertical ionization potential.
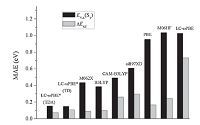
The parameter ω in RS functionals exhibits significant system- dependence characteristics. By employing RS methodology, Penfold [85] and Sun et al. [78] obtained optimal v values based on LC-BLYP and LC-ωPBE functionals, respectively, for a series of TADF molecules. Their results indicate that the tuned v values (0.14-0.20 bohr-1) decrease by half compared to their corresponding default values (0.33-0.40 bohr-1). The calculated mean absolute errors (MAE) between the theoretical and experimental data (Fig. 8) further shows that the corresponding optimally-tuned RS functionals can significantly reduce error by up to one order of magnitude, with MAEs of 0.15 eV for the lowest singlet excitation energies and 0.07 eV for the singlet-triplet gaps, compared to their non-tuned versions or other traditional functionals.
|
Download:
|
| Figure 8. Statistical analysis including mean absolute errors (MAE, eV) obtained via comparison between theoretical and experimental data for various density functionals. Reproduced with permission from ref [76]. Copyright 2015 American Chemical Society. | |
Although the tuning method returns very accurate results, tuned RS functionals have also been shown to overestimate the vertical excitation energies of PhCz, NPh3, and CBP (Fig. 5) possessing weak charge-transfer characteristics (Table 1). In addition, they may underestimate the significant charge-transfer molecules accompanying small CT transition distance, i.e., the excitation energies of 4CzIPN, 4CzPN, 4CzTPN, 4CzTPN-Me (Fig. 5), which were underestimated by roughly 0.3 eV (Table 1).
Although the universality of the tuning method needs further improvement, it is generally reliable and can simultaneously provide accurate predictions for lowest singlet and triplet excitation energies. To this effect, the prediction of singlet-triplet gaps is real instead of the result of error cancellation. Further, the success of optimally-tuned RS density functionals relies on a reasonable balance among the description of electronic localized and delocalized characteristics that are critically important for organic π-conjugated systems. The tuning approach can efficiently eliminate the so-called delocalization error [95, 96] and has correct asymptotic behavior within the long-range limit, which are not guaranteed for traditional density functionals. Finally, it is important to note that the traditional way to obtain optimal v value is based on a fitting approach and requires a large number of single-point calculations for cation, anion, and neutral systems. To further improve the efficiency of the tuning procedure, Sun et al. developed a "golden-ratio" method for searching the optimal ω parameters; their method can provide highly precise ω in relatively few steps [78, 94].
4. ConclusionsIn this review, we discussed several challenges and problemsolving strategies related to the TDDFT prediction of TADF. After excluding inappropriate ways of determining experimental and theoretical transition energies, the accurate prediction for vertical and zero-zero transition energies of TADF molecules appears to be highly dependent on the asymptotic behavior of the chosen XC- functionals. To a certain extent, the newly developed descriptor- OHF method and the optimally-tuned RS functionals eliminate the parameter selection problem in TDDFT, though their efficiency merits further improvement.
In addition to TADF materials for OLEDs, ICT compounds have shown considerable potential for application in organic photonics and electronics such as organic solar cells, sensors, probes, and nonlinear optics. A computer method that can accurately and rapidly predict the photophysical parameters of various ICT molecules would significantly promote innovative development in these fields.
Acknowledgment We are grateful to the Exploratory Research for Advanced Technology (ERATO) of Japan and the Key Special Program of the Ministry of Science and Technology of China (No. 2016YFB0401000) for financial support.| [1] | S. Boudin. Phosphorescence of glycerol solutions of eosin, influence of iodides. J. Chim. Phys. 27 (1930) 285–290. |
| [2] | G.N. Lewis, D. Lipkin, T.T. Magel. Reversible photochemical processes in rigid media. A study of the phosphorescent State. J. Am. Chem. Soc. 63 (1941) 3005–3018. DOI:10.1021/ja01856a043 |
| [3] | C. Parker, C. Hatchard. Triplet-singlet emission in fluid solutions. Phosphorescence of eosin. Trans. Faraday Soc. 57 (1961) 1894–1904. DOI:10.1039/tf9615701894 |
| [4] | J. Saltiel, H.C. Curtis, L. Metts, et al. Delayed fluroescence and phosphorescence of aromatic ketones in solution. J. Am. Chem. Soc. 92 (1970) 410–411. DOI:10.1021/ja00705a617 |
| [5] | A. Endo, K. Sato, K. Yoshimura, et al. Efficient up-conversion of triplet excitons into a singlet state and its application for organic light emitting diodes. Appl. Phys. Lett. 98 (2011) 083302. DOI:10.1063/1.3558906 |
| [6] | K. Goushi, K. Yoshida, K. Sato, et al. Organic light-emitting diodes employing efficient reverse intersystem crossing for triplet-to-singlet state conversion. Nat. Photon. 6 (2012) 253–258. DOI:10.1038/nphoton.2012.31 |
| [7] | T. Nakagawa, S.Y. Ku, K.T. Wong, et al. Electroluminescence based on thermally activated delayed fluorescence generated by a spirobifluorene donor-acceptor structure. Chem. Commun. 48 (2012) 9580–9582. DOI:10.1039/c2cc31468a |
| [8] | Q. Zhang, J. Li, K. Shizu, et al. Design of efficient thermally activated delayed fluorescence materials for pure blue organic light emitting diodes. J. Am. Chem. Soc. 134 (2012) 14706–14709. DOI:10.1021/ja306538w |
| [9] | S.Y. Lee, T. Yasuda, H. Nomura, et al. High-efficiency organic light-emitting diodes utilizing thermally activated delayed fluorescence from triazine-based donor-acceptor hybrid molecules. Appl. Phys. Lett. 101 (2012) 093306. DOI:10.1063/1.4749285 |
| [10] | G. Méhes, H. Nomura, Q. Zhang, et al. Enhanced electroluminescence efficiency in a spiro-acridine derivative through thermally activated delayed fluorescence. Angew Chem. Int. Ed. Engl. 51 (2012) 11311–11315. DOI:10.1002/anie.201206289 |
| [11] | H. Tanaka, K. Shizu, H. Miyazaki, et al. Efficient green thermally activated delayed fluorescence (TADF) from a phenoxazine-triphenyltriazine (PXZ-TRZ) derivative. Chem. Commun. 48 (2012) 11392–11394. DOI:10.1039/c2cc36237f |
| [12] | H. Uoyama, K. Goushi, K. Shizu, et al. Highly efficient organic light-emitting diodes from delayed fluorescence. Nature 492 (2012) 234–238. DOI:10.1038/nature11687 |
| [13] | K. Sato, K. Shizu, K. Yoshimura, et al. Organic luminescent molecule with energetically equivalent singlet and triplet excited states for organic light-emitting diodes. Phys. Rev. Lett. 110 (2013) 247401. DOI:10.1103/PhysRevLett.110.247401 |
| [14] | J. Li, T. Nakagawa, J. MacDonald, et al. Highly efficient organic light-emitting diode based on a hidden thermally activated delayed fluorescence channel in a heptazine derivative. Adv. Mater. 25 (2013) 3319–3323. DOI:10.1002/adma.v25.24 |
| [15] | Q. Zhang, B. Li, S. Huang, et al. Efficient blue organic light-emitting diodes employing thermally activated delayed fluorescence. Nat. Photon. 8 (2014) 326–332. DOI:10.1038/nphoton.2014.12 |
| [16] | Q. Zhang, H. Kuwabara, W.J. Potscavage Jr., et al. Anthraquinone-based intramolecular charge-transfer compounds: computational molecular design, thermally activated delayed fluorescence, and highlyefficientred electroluminescence. J. Am. Chem. Soc. 136 (2014) 18070–18081. DOI:10.1021/ja510144h |
| [17] | S. Hirata, Y. Sakai, K. Masui, et al. Highly efficient blue electroluminescence based on thermally activated delayed fluorescence. Nat. Mater. 14 (2015) 330–336. |
| [18] | Y. Tao, K. Yuan, T. Chen, et al. Thermally activated delayed fluorescence materials towards the breakthrough of organoelectronics. Adv. Mater. 26 (2014) 7931–7958. DOI:10.1002/adma.v26.47 |
| [19] | F.B. Dias, K.N. Bourdakos, V. Jankus, et al. Triplet harvesting with 100% efficiency by way of thermally activated delayed fluorescence in charge transfer OLED emitters. Adv. Mater. 25 (2013) 3707–3714. DOI:10.1002/adma.v25.27 |
| [20] | H. Wang, L. Xie, Q. Peng, et al. Novel Thermally activated delayed fluorescence materials-thioxanthone derivatives and their applications for highly efficient OLEDs. Adv. Mater. 26 (2014) 5198–5204. DOI:10.1002/adma.201401393 |
| [21] | X.-K. Liu, Z. Chen, C.-J. Zheng, et al. Prediction and design of efficient exciplex emitters for high-efficiency, thermally activated delayed-fluorescence organic light-emitting diodes. Adv. Mater. 27 (2015) 2378–2383. DOI:10.1002/adma.v27.14 |
| [22] | M. Kim, S.K. Jeon, S.-H. Hwang, et al. Stable blue thermally activated delayed fluorescent organic light-emitting diodes with three times longer lifetime than phosphorescent organic light-emitting diodes. Adv. Mater. 27 (2015) 2515–2520. DOI:10.1002/adma.201500267 |
| [23] | L. Mei, J. Hu, X. Cao, et al. The inductive-effect of electron withdrawing trifluoromethyl for thermally activated delayed fluorescence: tunable emission from tetra- to penta-carbazole in solution processed blue OLEDs. Chem. Commun. 51 (2015) 13024–13027. DOI:10.1039/C5CC04126K |
| [24] | T. Hatakeyama, K. Shiren, K. Nakajima, et al. Ultrapure blue thermally activated delayed fluorescence molecules: Efficient HOMO-LUMO separation by the multiple resonance effect. Adv. Mater. 28 (2016) 2777–2781. DOI:10.1002/adma.v28.14 |
| [25] | P. Rajamalli, N. Senthilkumar, P. Gandeepan, et al. A thermally activated delayed blue fluorescent emitter with reversible externally tunable emission. J. Mater. Chem. C 4 (2016) 900–904. DOI:10.1039/C5TC03943F |
| [26] | S. Feuillastre, M. Pauton, L. Gao, et al. Design and synthesis of new circularly polarized thermally activated delayed fluorescence emitters. J. Am. Chem. Soc. 138 (2016) 3990–3993. DOI:10.1021/jacs.6b00850 |
| [27] | D. Zhang, M. Cai, Y. Zhang, et al. Sterically shielded blue thermally activated delayed fluorescence emitters with improved efficiency and stability. Mater. Horizons 3 (2016) 145–151. DOI:10.1039/C5MH00258C |
| [28] | G. Xie, X. Li, D. Chen, et al. Evaporation- and solution-process-feasible highly efficient thianthrene-9,90,10,100-tetraoxide-based thermally activated delayed fluorescence emitters with reduced efficiency roll-off. Adv. Mater. 28 (2016) 181–187. DOI:10.1002/adma.201503225 |
| [29] | M.E. Casida, Response Theory for Molecules, Recent Advances in Density Functional Methods: (Part I), vol. 1, 1995, p. 155. |
| [30] | E. Gross, J. Dobson, M. Petersilka, Density functional theory of time-dependent phenomena, in: Density Functional Theory II, Springer, 1996, pp. 81-172. |
| [31] | A. Dreuw, M. Head-Gordon. Single-reference ab initio methods for the calculation of excited states of large molecules. Chem. Rev. 105 (2005) 4009–4037. DOI:10.1021/cr0505627 |
| [32] | L. Serrano-Andrés, J.J. Serrano-Pérez, Calculation of excited states: molecular photophysics and photochemistry on display, in: Handbook of Computational Chemistry, Springer, 2012, pp. 483-560. |
| [33] | D. Jacquemin, A. Planchat, C. Adamo, et al. TD-DFT assessment of functionals for optical 0-0 transitions in solvated dyes. J. Chem. Theory Comput. 8 (2012) 2359–2372. DOI:10.1021/ct300326f |
| [34] | C. Adamo, D. Jacquemin. The calculations of excited-state properties with timedependent density functional theory. Chem. Soc. Rev. 42 (2013) 845–856. DOI:10.1039/C2CS35394F |
| [35] | S. Grimme, Calculation of the electronic spectra of large molecules, in: Reviews in Computational Chemistry, John Wiley & Sons, Inc., 2004, pp. 153-218. |
| [36] | A. Dreuw, M. Head-Gordon. Failure of time-dependent density functional theory for long-range charge-transfer excited states: the zincbacteriochlorin-bacteriochlorin and bacteriochlorophyll-spheroidene complexes. J. Am. Chem. Soc. 126 (2004) 4007–4016. DOI:10.1021/ja039556n |
| [37] | S. Huang, Q. Zhang, Y. Shiota, et al. Computational prediction for singlet- and triplet-transition energies of charge-transfer compounds. J. Chem. Theory Comput. 9 (2013) 3872–3877. DOI:10.1021/ct400415r |
| [38] | S. Hirata, M. Head-Gordon. Time-dependent density functional theory within the Tamm-Dancoff approximation. Chem. Phys. Lett. 314 (1999) 291–299. DOI:10.1016/S0009-2614(99)01149-5 |
| [39] | M.J.G. Peach, M.J. Williamson, D.J. Tozer. Influence of triplet instabilities in TDDFT. J. Chem. Theory Comput. 7 (2011) 3578–3585. DOI:10.1021/ct200651r |
| [40] | M. Moral, L. Muccioli, W.J. Son, et al. Theoretical rationalization of the singlet-triplet gap in OLEDs materials: Impact of charge-transfer character. J. Chem. Theory Comput. 11 (2015) 168–177. DOI:10.1021/ct500957s |
| [41] | B. Milián-Medina, J. Gierschner. Computational design of low singlet-triplet gap all-organic molecules for OLED application. Org. Electron. 13 (2012) 985–991. DOI:10.1016/j.orgel.2012.02.010 |
| [42] | G. Scalmani, M.J. Frisch. Continuous surface charge polarizable continuum models of solvation. I. General formalism. J. Chem. Phys. 132 (2010) 114110. DOI:10.1063/1.3359469 |
| [43] | V. Barone, M. Cossi. Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model. J. Phys. Chem. A 102 (1998) 1995–2001. DOI:10.1021/jp9716997 |
| [44] | M. Cossi, N. Rega, G. Scalmani, etal.. Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. J. Comput. Chem. 24 (2003) 669–681. DOI:10.1002/jcc.10189 |
| [45] | R. Improta, V. Barone, G. Scalmani, et al. A state-specific polarizable continuum model time dependent density functional theory method for excited state calculations in solution. J. Chem. Phys. 125 (2006) 054103. DOI:10.1063/1.2222364 |
| [46] | R.Improta, G.Scalmani, M.J.Frisch, etal.. Toward effective andreliable fluorescence energies in solution by a new state specific polarizable continuum model time dependent density functional theory approach. J. Chem. Phys. 127 (2007) 074504. DOI:10.1063/1.2757168 |
| [47] | A. Klamt. The COSMO and COSMO-RS solvation models. WIRES Comput. Mol. Sci. 1 (2011) 699–709. DOI:10.1002/wcms.56 |
| [48] | J. Tomasi, R. Bonaccorsi. Methodological aspects of the solvation models based on continuous solvent distributions. Croat. Chem. Acta 65 (1992) 29–54. |
| [49] | A.V. Marenich, C.J. Cramer, D.G. Truhlar. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 113 (2009) 6378–6396. DOI:10.1021/jp810292n |
| [50] | A. Nicholls, D.L. Mobley, J.P. Guthrie, et al. Predicting small-molecule solvation free energies: an informal blind test for computational chemistry. J. Med. Chem. 51 (2008) 769–779. DOI:10.1021/jm070549+ |
| [51] | J. Lu, Y. Zheng, J. Zhang. Tuning the color of thermally activated delayed fluorescent properties for spiro-acridine derivatives by structural modification of the acceptor fragment: a DFT study. RSC Adv. 5 (2015) 18588–18592. DOI:10.1039/C4RA15155K |
| [52] | M. Klessinger, J. Michl, Excited States and Photochemistry of Organic Molecules, 1995, p. 124. |
| [53] | D.J. Casadonte, D.R. McMillin. Hindered internal conversion in rigid media. Thermally nonequilibrated 3IL and 3CT emissions from[Cu(5-X-phen)(PPh3)2]+ and[Cu(4,7-X2-phen)(PPh3)2]+ systems in a glass at 77 K. J. Am. Chem. Soc. 109 (1987) 331–337. DOI:10.1021/ja00236a006 |
| [54] | P. Klán, J. Wirz, Photochemistry of Organic Compounds: From Concepts to Practice, John Wiley & Sons, 2009, p. 43. |
| [55] | B. Wardle, Principles and Applications of Photochemistry, John Wiley & Sons, 2009, p. 61. |
| [56] | Q. Zhang, T. Komino, S. Huang, et al. Triplet exciton confinement in green organic light-emitting diodes containing luminescent charge-transfer Cu(I) complexes. Adv. Funct. Mater. 22 (2012) 2327–2336. DOI:10.1002/adfm.v22.11 |
| [57] | J. Li, Q. Zhang, H. Nomura, et al. Thermally activated delayed fluorescence from 3nπ* to 1nπ* up-conversion and its application to organic light-emitting diodes. Appl. Phys. Lett. 105 (2014) 013301. DOI:10.1063/1.4887346 |
| [58] | A.D. Becke. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98 (1993) 5648. DOI:10.1063/1.464913 |
| [59] | C. Adamo, V. Barone. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 110 (1999) 6158–6170. DOI:10.1063/1.478522 |
| [60] | Y. Zhao, D.G. Truhlar. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 120 (2008) 215–241. DOI:10.1007/s00214-007-0310-x |
| [61] | T. Yanai, D.P. Tew, N.C. Handy. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 393 (2004) 51–57. DOI:10.1016/j.cplett.2004.06.011 |
| [62] | H. Iikura, T. Tsuneda, T. Yanai, et al. A long-range correction scheme for generalized-gradient-approximation exchange functionals. J. Chem. Phys. 115 (2001) 3540–3544. DOI:10.1063/1.1383587 |
| [63] | O.A. Vydrov, G.E. Scuseria. Assessment of a long-range corrected hybrid functional. J. Chem. Phys. 125 (2006) 234109. DOI:10.1063/1.2409292 |
| [64] | J.-D. Chai, M. Head-Gordon. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 10 (2008) 6615–6620. DOI:10.1039/b810189b |
| [65] | S.Y. Lee, T. Yasuda, Y.S. Yang, et al. Luminous butterflies: Efficient exciton harvesting by benzophenone derivatives for full-color delayed fluorescence OLEDs. Angew Chem. Int. Ed. Engl. 53 (2014) 6402–6406. DOI:10.1002/anie.201402992 |
| [66] | K. Kawasumi, T. Wu, T. Zhu, et al. Thermally activated delayed fluorescence materials based on homoconjugation effect of donor-acceptor triptycenes. J. Am. Chem. Soc. 137 (2015) 11908–11911. DOI:10.1021/jacs.5b07932 |
| [67] | Y. Sagara, K. Shizu, H. Tanaka, et al. Highly efficient thermally activated delayed fluorescence emitters with small singlet-triplet energy gap and large oscillator strength. Chem. Lett. 44 (2015) 360–362. DOI:10.1246/cl.141054 |
| [68] | S. Wang, X. Yan, Z. Cheng, et al. Highly Efficient near-infrared delayed fluorescence organic light emitting diodes using a phenanthrene-based charge-transfer compound. Angew Chem. Int. Ed. Engl. 54 (2015) 13068–13072. DOI:10.1002/anie.v54.44 |
| [69] | P. Rajamalli, N. Senthilkumar, P. Gandeepan, et al. A new molecular design based on thermally activated delayed fluorescence for highly efficient organic light emitting diodes. J. Am. Chem. Soc. 138 (2015) 628–634. |
| [70] | X. Zhang, W. Shen, D. Zhang, et al. Theoretical investigation of dihydroacridine and diphenylsulphone derivatives as thermally activated delayed fluorescence emitters for organic light-emitting diodes. RSC Adv. 5 (2015) 51586–51591. DOI:10.1039/C5RA04929F |
| [71] | K. Shizu, H. Noda, H. Tanaka, et al. Highly efficient blue electroluminescence using delayed-fluorescence emitters with large overlap density between luminescent and ground states. J. Phys. Chem. C 119 (2015) 26283–26289. DOI:10.1021/acs.jpcc.5b07798 |
| [72] | K. Shizu, M. Uejima, H. Nomura, et al. Enhanced electroluminescence from a thermally activated delayed-fluorescence emitter by suppressing nonradiative decay. Phy. Rev. Appl. 3 (2015) 014001. DOI:10.1103/PhysRevApplied.3.014001 |
| [73] | J. Lee, K. Shizu, H. Tanaka, et al. Oxadiazole- and triazole-based highly-efficient thermally activated delayed fluorescence emitters for organic light-emitting diodes. J. Mater. Chem. C 1 (2013) 4599–4604. |
| [74] | J. Lee, K. Shizu, H. Tanaka, et al. Controlled emission colors and singlet-triplet energy gaps of dihydrophenazine-based thermally activated delayed fluorescence emitters. J. Mater. Chem. C 3 (2015) 2175–2181. DOI:10.1039/C4TC02530J |
| [75] | A. Karton, A. Tarnopolsky, J.-F. Lamère, et al. Highly accurate first-principles benchmark data sets for the parametrization and validation of density functional and other approximate methods. derivation of a robust, generally applicable, double-hybrid functional for thermochemistry and thermochemical kinetics. J. Phys. Chem. A 112 (2008) 12868–12886. DOI:10.1021/jp801805p |
| [76] | L. Goerigk, S. Grimme. Efficient and accurate double-hybrid-meta-GGA density functionals-evaluation with the extended GMTKN30 database for general main group thermochemistry, kinetics, and noncovalent interactions. J. Chem. Theory Comput. 7 (2011) 291–309. DOI:10.1021/ct100466k |
| [77] | A.D. Becke. Perspective: fifty years of density-functional theory in chemical physics. J. Chem. Phys. 140 (2014) 18A. |
| [78] | H. Sun, C. Zhong, J.-L. Brédas. Reliable prediction with tuned range-separated functionals of the singlet-triplet gap in organic emitters for thermally activated delayed fluorescence. J. Chem. Theory Comput. 11 (2015) 3851–3858. DOI:10.1021/acs.jctc.5b00431 |
| [79] | M.J.G. Peach, P. Benfield, T. Helgaker, et al. Excitation energies in density functional theory: an evaluation and a diagnostic test. J. Chem. Phys. 128 (2008) 044118. DOI:10.1063/1.2831900 |
| [80] | T. Le Bahers, C. Adamo, I. Ciofini. A qualitative index of spatial extent in chargetransfer excitations. J. Chem. Theory Comput. 7 (2011) 2498–2506. DOI:10.1021/ct200308m |
| [81] | C.A. Guido, P. Cortona, B. Mennucci, et al. On the metric of charge transfer molecular excitations: a simple chemical descriptor. J. Chem. Theory Comput. 9 (2013) 3118–3126. DOI:10.1021/ct400337e |
| [82] | T. Etienne, X. Assfeld, A. Monari. Toward a quantitative assessment of electronic transitions' charge-transfer character. J. Chem. Theory Comput. 10 (2014) 3896–3905. DOI:10.1021/ct5003994 |
| [83] | C.A. Guido, P. Cortona, C. Adamo. Effective electron displacements: a tool for timedependent density functional theory computational spectroscopy. J. Chem. Phys. 140 (2014) 104101. DOI:10.1063/1.4867007 |
| [84] | T. Etienne. Transition matrices and orbitals from reduced density matrix theory. J. Chem. Phys. 142 (2015) 244103. DOI:10.1063/1.4922780 |
| [85] | T.J. Penfold. On predicting the excited-state properties of thermally activated delayed fluorescence emitters. J. Phys. Chem. C 119 (2015) 13535–13544. DOI:10.1021/acs.jpcc.5b03530 |
| [86] | T. Chen, L. Zheng, J. Yuan, et al. Understanding the control of singlet-triplet splitting for organic exciton manipulating: a combined theoretical and experimental approach. Sci. Rep. 5 (2015) 10923. DOI:10.1038/srep10923 |
| [87] | R. Baer, E. Livshits, U. Salzner. Tuned range-separated hybrids in density functional theory. Annu. Rev. Phys. Chem. 61 (2010) 85–109. DOI:10.1146/annurev.physchem.012809.103321 |
| [88] | T. Stein, H. Eisenberg, L. Kronik, et al. Fundamental gaps in finite systems from eigenvalues of a generalized Kohn-Sham method. Phys. Rev. Lett. 105 (2010) 266802. DOI:10.1103/PhysRevLett.105.266802 |
| [89] | J. Autschbach, M. Srebro. Delocalization error and "functional tuning" in Kohn-Sham calculations of molecular properties. Acc. Chem. Res. 47 (2014) 2592–2602. DOI:10.1021/ar500171t |
| [90] | L. Kronik, T. Stein, S. Refaely-Abramson, et al. Excitation gaps of finite-sized systems from optimally tuned range-separated hybrid functionals. J. Chem. Theory Comput. 8 (2012) 1515–1531. DOI:10.1021/ct2009363 |
| [91] | H. Sun, J. Autschbach. Electronic energy gaps for p-conjugated oligomers and polymers calculated with density functional theory. J. Chem. Theory Comput. 10 (2014) 1035–1047. DOI:10.1021/ct4009975 |
| [92] | H. Sun, Z. Hu, C. Zhong, et al. Quantitative estimation of exciton binding energy of polythiophene-derived polymers using polarizable continuum model tuned range-separated density functional. J. Phys. Chem. C 120 (2016) 8048–8055. DOI:10.1021/acs.jpcc.6b01975 |
| [93] | H. Sun, S. Zhang, Z. Sun. Applicability of optimal functional tuning in density functional calculations of ionization potentials and electron affinities of adeninethymine nucleobase pairs and clusters. Phys. Chem. Chem. Phys. 17 (2015) 4337–4345. DOI:10.1039/C4CP05470A |
| [94] | H. Sun, S. Zhang, C. Zhong, et al. Theoretical study of excited states of DNA base dimers and tetramers using optimally tuned range-separated density functional theory. J. Comput. Chem. 37 (2016) 684–693. DOI:10.1002/jcc.v37.7 |
| [95] | M.A. Rohrdanz, J.M. Herbert. Simultaneous benchmarking of ground- and excitedstate properties with long-range-corrected density functional theory. J. Chem. Phys. 129 (2008) 034107. DOI:10.1063/1.2954017 |
| [96] | P. Mori-Sánchez, A.J. Cohen, W. Yang. Localization and delocalization errors in density functional theory and implications for band-gap prediction. Phys. Rev. Lett. 100 (2008) 146401. DOI:10.1103/PhysRevLett.100.146401 |
 2016, Vol. 27
2016, Vol. 27