Two-dimensional (2D) correlation spectroscopy [1] is a versatile analytical technique which has become popular in the last several decades. It initially started as an obscure data sorting technique for rheo-optical study of polymer films undergoing small amplitude repetitive deformation [1a, 1c]. With the introduction of the generalized correlation concept in 1993 [1d] and subsequent development of an efficient numerical algorithm to compute 2D spectra [1e, 1f],this technique has gained remarkable popularity in a broad area of analytical science as one of the mainstream spectral data analysis methods [1g].
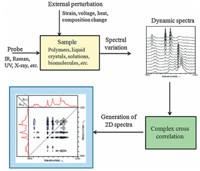
Fig. 1 shows the general description of 2D correlation analysis scheme. In 2D correlation spectroscopy,a sample under the spectroscopic observation is stimulated by applying an external perturbation,which induces systematic changes in the spectral intensity of the sample system. The observed spectrum thus becomes a function not only of the standard spectral variable,such as infrared wavenumber or Raman shift,but also of other physical variable representing the effect of the applied perturbation,such as time,temperature,and composition. A new set of spectra defined by two independent spectral axes are then generated by applying a form of cross correlation analysis to the spectral intensity changes along the perturbation variable.
|
Download:
|
| Fig. 1. Schematic representation of generalized 2D correlation spectroscopy. Complex cross correlation analysis of the variation of spectral intensities induced by external perturbations generates 2D correlation spectra. | |
Notable features of 2D correlation spectroscopy are: simplification of complex spectra consisting of many overlapped peaks,enhancement of apparent spectral resolution by spreading peaks over the second dimension,establishment of unambiguous assignment through correlation of bands selectively coupled by various interaction mechanisms,and determination of the sequence of events represented by the variations of spectral intensities. A wide scope of fundamental and practical spectroscopic research work has been conducted by taking advantages of unique and advantageous features of 2D correlation spectra [2]. In this review,some of the key developments in this field are highlighted.
2. Diverse applications and opportunitiesAs already implied in the generic scheme depicted in Fig. 1, there is no intrinsic limitation in 2D correlation analysis for the selection of specific spectroscopic or analytical probes,nature of external perturbations applied to the sample,and type and state of the sample systems to be studied. This flexibility makes 2D correlation spectroscopy a truly general and extremely versatile analytical tool. A broad range of applications of 2D correlation spectroscopy techniques have been well documented by a series of review articles compiled in the past [2].
For example,a comprehensive review [2h] on various perturbation methods,analytical probes and specific areas of applications has recently been compiled. Types of perturbation methods found in the published literature are amazingly diverse, encompassing both dynamic and static effects. Flexibility in the type of analytical probes used in 2D correlation is also noted. Aside from IR spectroscopy,which is the most commonly used tool in the field today,many other spectroscopic and analytical probes are used in 2D correlation analysis. Fields of applications covered by the literature are also very broad,ranging from fundamental research to practical applications in a number of physical,chemical and biological systems.
Dynamic perturbations used in 2D correlation spectroscopy may be time-dependent physical processes,such as acoustic effect or pulsed mechanical deformation,sorption,penetration,diffusion and evaporation of molecules,crystallization,and many other transient physical phenomena. They also include chemical reactions,like polymerization and crosslinking,and a number of biological processes,as well as duration of exposure to various stimuli,such as radiation dose. Static perturbations are much more commonly employed today in 2D correlation spectroscopy than dynamic counterpart. The most popular is the effect of temperature, which includes many different phenomena,such as conformational changes of proteins,molecular associations,selfassembly and gelation,hydrogen bonding interactions,melting, crystallization,and glass transition,and other transition phenomena, various structural changes,and various temperature-induced chemical reactions. Aside from temperature,the influence of concentration,such as pH effect,compositions of solution mixtures,electrolytes and ionic liquid solutions,dissolved gasses, blends and composites,and the use of designed concentration series,are also reported. Other static perturbations often used include various electro-magnetic effects,mechanical deformation, pressure and compression,and even spatial distributions.
Analytical probes employed are currently dominated by infrared (IR),but other probes are also used,such as Raman,near infrared (NIR),UV-visible,THz and fluorescence,NMR,X-ray spectroscopy and scattering techniques,and other analytical methods,like mass spectrometry and chromatography. Combined use of different analytical probes leads to the powerful technique of hetero-spectral correlation analysis,such as IR-NIR correlation. This topic will be separately discussed later. The ever expanding depth,breadth and versatility of 2D correlation spectroscopy and its applications all point to the robust and healthy state of the field.
Among the type of applications,polymers are most often extensively studied,including bio-based and biodegradable polymers,thermo-responsive polymers,water-soluble polymers, liquid crystalline polymers,thermosetting polymers,block copolymers and blends,a number of conventional polymers,as well as polymer matrices incorporating small molecules within. Other materials studied by 2D correlation spectroscopy include nanoparticles and nano-composites,proteins,and peptides,and other biomolecules,bio-based materials and actual living cells,food products,and environmental samples. 2D correlation spectroscopy is used in medical,physiological,and pharmaceutical applications, authentication of traditional Chinese medicines,analyses of liquids and solution mixtures,colloids,interfaces,and electrode surfaces, inorganic-organic hybrids and ionic species,industrial chemicals, and various reaction systems. Specific literature citations related to these areas are found in the recent comprehensive review [2h].
3. Noteworthy developments in 2D correlation spectroscopyIn recent years,a number of unique and different types of 2D correlation spectroscopy techniques have been introduced. In this review,several noteworthy forms of 2D correlation spectroscopy techniques are highlighted. More specifically,hetero-spectral correlation [3, 4, 5] and multiple perturbation correlation techniques [6],including orthogonal sample design [7],will be discussed in some detail. Other equally important and interesting forms of 2D correction spectroscopy techniques are also briefly discussed with pertinent literature citations [8].
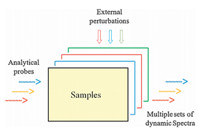
3.1. Hetero-correlation analysisHetero-correlation analysis [3, 4, 5] is a unique and powerful feature of generalized 2D correlation spectroscopy with a large potential of utility for various scientific applications. In heterocorrelation studies,2D correlation spectra are obtained from two distinct sets of spectral data arising from different conditions. The degree of correlation is then examined between two different types of spectroscopic data. There are actually three distinct types of hetero-correlation techniques: hetero-spectral correlation,hetero- perturbation correlation,and hetero-sample correlation. Fig. 2 shows the schematic representations of various hetero-correlation techniques.
|
Download:
|
| Fig. 2. Three types of 2D hetero-correlation analysis. 2D spectra are generated by comparing a pair of dynamic spectra arising from different probes (hetero-spectral correlation),different perturbations (hetero-perturbation or hybrid correlation),or different samples (hetero-sample correlation). | |
By far the most commonly used form of hetero-correlation analysis is the hetero-spectral correlation [3]. In hetero-spectral correlation analysis,two distinct spectroscopic probes,such as IR and Raman,are used. Systematic variations of different spectral signals are observed for the same sample,or at least very similar samples,under the similar perturbation condition for comparison. One of the earliest known examples of such hetero-spectral correlation analysis was reported for the combined measurement of IR dichroism and small-angle X-ray scattering signals of a block copolymer sample under periodic deformation [3a]. Nowadays, many other types of hetero-correlation studies are reported. In contrast,hetero-sample correlation [4] utilizes dynamic spectra collected from two different samples under a common perturbation by using the same analytical probe. Finally,in heteroperturbation correlation [5],a sample is stimulated by two different perturbation methods,leading to the so-called hybrid correlation analysis. Some examples of hetero-correlation studies are discussed below.
Hetero-spectral correlation between mid IR and NIR signals [3b, 3g] offers an interesting opportunity to combine the advantages of the two vibrational spectroscopy techniques. The experimental ease of NIR spectroscopy makes this technique a preferred analytical probe for many practical applications. Mid IR spectra,on the other hand,have much better resolved spectral features and consequently well-established band assignments. It is natural to combine the strength of IR and NIR spectroscopy by using 2D correlation technique. The first 2D correlation analysis between IR and NIR spectra was reported by Barton et al. [3b]. Since then many other IR and NIR hetero-spectral correlation studies have been reported. Some of the recent reports include diverse data analyses,such as rehydration process of amylopectin starch extracted from glutinous rice flour [3c],ethanol content determination during a fermentation process [3d],monitoring of epoxy resin curing reaction [3e],and botanical biomass changes under roasting process [3f].
Other types of spectroscopic probes are also combined with IR to generate hetero-correlation spectra. For example,IR-Raman hetero-spectral correlation [3g] to investigate thermal dynamics of natural killer cell receptor proteins was reported. The possibility of comparing and relating IR and CD spectra [3h] was also considered for the hetero-spectral correlation analysis. The correlation between XPS and IR spectra [3i] was used to study semi-crystalline copolymers under increasing temperature by taking advantage of the different sensitivities of the two probes to molecular environment. 2D hetero-spectral correlation between IR and UV-visible spectra [3j] was reported for the study of aggregate formation process of marine mucilage as a function of incubation period. The correlation between IR and NMR [3k] for free radical polymerization process was also reported to gain unambiguous band assignments.
The application of 2D hetero-spectral correlation technique is not limited to the comparison of molecular spectra. For example, hetero-correlation between small angle X-ray scattering (SAXS) and wide-angle X-ray diffraction (WAXD) was reported for nonisothermal crystallization of hydrogenated polybutadiene with varying time and temperature [3l] and for the study of multiplestep isothermal crystallization of a biodegradable polymer [3m]. Hetero-correlation was applied between charge and mass [3n] for cyclic voltammetry study. Hetero-chromatographic correlation [3o] was reported between two detection systems used in HPLC study of valorization of olive stones employed to increase sugar content.
Hetero-sample or hetero-system correlation [4] is an interesting variant form of hetero-correlation analysis,where the existence or lack of correlation is examined among spectral intensity variations of different samples by using the same analytical probe and perturbation condition. In certain cases, explicit constraint imposed by using the common perturbation conditions is utilized [4a, 4c]. Such a constraint makes the technique distinct from simple covariance [4d],correlation coefficient [3b],or conventional statistical correlation analysis [4e] applied for spectra collected from different samples. This technique encompasses the so-called cross spectral correlation analysis proposed by Dai and coworkers [4a, 4b],which is a clever use of hetero-sample correlation analysis for time-resolved emission spectra of transient radicals from different of samples. Hetero-system correlation was recently applied for the timedependent evaporation of ethanol mixed with oleic acid or linoleic acid [4c].
The concept of hybrid correlation was originally proposed by Wu et al. [5a] to explore the implicit relationship between two different perturbation effects influencing the sample. It can be viewed as a form of more general class of hetero-correlation technique called hetero-perturbation correlation analysis [5]. In hetero-perturbation correlation,spectral intensity variations to be correlated are induced by applying different types of external perturbations to the same sample. Unlike the multiple perturbation 2D correlation analysis to be discussed later,different perturbations are applied one perturbation at a time. Hybrid correlation explores the underlying similarity or differences of the effect of applied perturbations through correlation analysis.
Recent examples include the hybrid 2D correlation study of coil-to-globule phase transition of poly(N-isopropylacrylamide) induced by both temperature and pressure [5b]. In another study, time evolutions under different pH for the H/D exchange study of immunoglobulin G were analyzed by hybrid correlation to probe the flexibility and dynamics of different region of the protein at different pH levels [5c]. Hybrid correlation was also used for the study of growth process of a plant pathogen by comparing NMR spectra obtained with and without phosphonate [5d] and for the analysis of concentration and temperature effects on solution mixtures [5e].
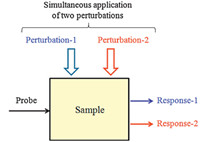
3.2. Multiple perturbation 2D correlation2D correlation analysis is traditionally carried out under a single perturbation applied to a system of interest. An interesting possibility arises when more than one type of external perturbations are simultaneously applied to the sample [6, 7]. This situation is different from the case for the previously mentioned heteroperturbation correlation study,where different type of perturbation, like temperature and pressure,is applied to the system one perturbation at a time. Fig. 3 shows the schematic representation of a multiple perturbation experiment. Here the effect of perturbation-1 on the response-1 may actually be influenced by the presence of additional perturbation-2,and vice versa. The possible existence of the interplay between two perturbation effects will lead to nonlinear responses of the system,which can be effectively detected by 2D correlation spectroscopy. This approach also greatly expands the design flexibility and diversity of 2D correlation analyses.
|
Download:
|
| Fig. 3. Multiple perturbation 2D correlation analysis. Two different perturbations are simultaneously applied to the sample to induce spectral intensity changes affected by both effects. | |
Shinzawa et al. [6a] studied Raman imaging data for the spatial distribution of actives in pharmaceutical tablets by 2D correlation. Instead of a single 2D spectrum,the evolution of a series of 2D spectra was obtained as a function of processing time spent for grinding. This work led to the development of multiple 2D correlation spectra generated under multiple perturbations of process conditions [6b]. Finely ground microcrystalline cellulose was observed by ATR IR under different evaporation time,which changes the water content of the sample,and also under different grinding time,which changes the morphology,crystallinity,and consequently the evaporation rate. A new set of formulae for calculating a number of different types of synchronous 2D spectra under multiple perturbation condition was proposed.
Multiple 2D correlation analysis of a system under the simultaneous influence of different perturbations has been further explored [6c, 6e]. Self-assembly of oleic acid under the combined double perturbation conditions consisting of both pressure and temperature variations generated three-way dataset [6c]. To manage the complexity of analysis,so-called partial 2D correlation was proposed by keeping the influence of one perturbation effect constant. In the NMR study of a nano-composite material containing clay particles under multiple perturbation of both temperature and clay composition,the concept of parallel factor (PARAFAC) kernel analysis was also introduced [6d]. Multiple perturbation 2D NIR correlation analysis was recently reported for pressure-induced variations of cellulose affecting the packing and crystallinity along with the effect of compositional changes by water absorption [6e].
3.3. Orthogonal sample designOrthogonal sample design (OSD) is an intriguing form of multiple perturbation correlation analysis [7]. The idea was originally forwarded by Xu of Peking University [7a, 7c]. In this scheme,a series of samples with carefully designed concentration profiles are prepared to maximize the pertinent information content of the resulting 2D correlation spectra. OSD utilizes a set of mixture samples,such that the dynamic concentration variations of two components are designed to become mathematically orthogonal to each other. Such a sample design effectively eliminates interfering cross peaks due exclusively to the linear dependence on concentration variation,i.e.,the Beer-Lambert law dependence.
Since two independent concentration variations (e.g.,of solutes P and Q in a solution) are simultaneously applied as perturbations to the system,OSD may be viewed as a form of multiple perturbation 2D correlation spectroscopy technique. In the scheme of Fig. 3,perturbation-1 and perturbation-2 are now designed to be orthogonal to each other. If response-1 (spectral band intensity change for species P) is proportional to perturbation-1 (concentration variation of species P) according to the Beer-Lambert law,and vice versa for species Q in terms of perturbation-2 and response-2, then the response-1 and response-2 must also become orthogonal to each other. But do they? If there is specific intermolecular interaction between species P and Q,their concentrations will be modified from the initial state,and their spectral intensity responses may no longer be strictly orthogonal.
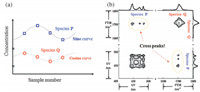
Fig. 4 shows the graphic representation showing how an OSD scheme with even a very simple concentration series design can be used for the detection of subtle intermolecular interaction. In this example,only four solution mixture samples containing the two solutes of interest are prepared (Fig. 4a). The concentration of solute P varies in a pattern similar to a sine function around a fixed value along the sequence of this solution mixture series. Meanwhile,that of the other solute Q is designed to follow the pattern of a cosine function. Since sine and cosine signals are mathematically orthogonal to each other, the correlation of the spectral intensities of P and Q along the mixture series should become zero,if the intensities are strictly proportional to the original solute concentrations. No cross peak should be observed in that case in synchronous 2D correlation spectrum.
|
Download:
|
| Fig. 4. (a) Orthogonal sample design (OSD) concentration series with the initial solute P concentration (before mixing with Q) varying as a sine function,while the solute Q as cosine function. (b) Presence of cross peaks between bands for solutes P and Q indicates that spectral intensity variations for P and Q are no longer orthogonal to each other due to intermolecular interactions. | |
On the other hand,if there is any specific intermolecular interaction which can modify the state of the solutes,e.g.,by association compound formation,the actual concentrations of P and Q after mixing are no longer the same as the initial concentrations without any interaction. In that case,the actual solute concentrations of P and Q in the mixture are no longer orthogonal to each other,and cross peak will be generated in the synchronous 2D spectrum as shown in Fig. 4b. In other words,OSD is a highly sensitive detection method for very subtle modification of the initial concentrations of two solutes caused by specific intermolecular interactions. Many other forms of concentration series have been designed to suppress the appearance of uninformative cross peaks from both synchronous and asynchronous spectra.
In practice,OSD was used first for simulated and experimental concentration-dependent UV-visible spectra of mixed solutions of NdCl3 and PrCl3 [7a]. Portion of spectra proportional to the solute content is effectively removed by the application of OSD scheme to reveal the apparent deviation from the Beer-Lambert law caused by the intermolecular interaction. Similarly,the application of OSD to the 2D UV and UV-IR hetero-spectral correlation was reported to detect the interaction between lanthanide (III) ions and organic ligands [7b]. This specific work was the basis for the example used in Fig. 4. The original OSD was modified [7c] to address the possibility of fortuitous cancellation of cross peaks,when there is real intermolecular interaction. The modified OSD takes advantages of the effect of measurement under different path lengths to provide unambiguous determination of an interaction. 2D UV- visible spectra of NdCl3/PrCl3 aqueous solution mixtures show no cross peaks under OSD regardless of path length change,indicating the lack of interaction.
In the recent years,the concept of OSD has been further refined to address some of the limitations of the original OSD scheme. In double orthogonal sample design (DOSD) [7d],concentrations of two components are set such that one series is not only simply orthogonal to but also strictly quadrature to (i.e.,90 degrees out of phase with) the other concentration series. In their first DOSD study,IR and UV-visible hetero-spectral correlation of benzene/I2/ CCl4 system was analyzed,and various peak cluster patterns were identified by an extensive simulation study reflecting the effects of frequency shift and band width changes.
Asynchronous orthogonal sample design (AOSD) further extends the OSD analysis to 2D asynchronous spectrum [7e]. Concentration series of butanone and dimethyl formamide in CCl4 were designed to eliminate peaks due to the uninformative effect not related to specific intermolecular interactions. Finally,double asynchronous orthogonal sample design (DAOSD) [7f] based on another set of concentration series eliminate interfering peaks and identify specific molecular interactions. It was used for 2D UV- visible and 2D IR study of iodine-benzene/CCl4 system. AOSD analysis based on concentration series of DMF and butanone in CCl4 was used [7g] to find that the sequence of concentration with four or more samples dramatically affects asynchronous spectra. The potential of AOSD was extended in their study of acetone- butanone interactions in CCl4 with varying concentration [7h]. A modified reference spectrum,which was derived from average of virtual mixture without intermolecular interactions,was used to improve the signal-to-noise ratio and to make the detection of weak signals possible.
3.4. Other noteworthy developmentsSome of the other important new concepts [8] in the field of 2D correlation spectroscopy are described in the recent comprehensive surveys [2f, 2g],so they are only briefly discussed here. Interested readers are referred to the original publications cited here for additional information.
Projection 2D correlation [8a] is a technique to attenuate or amplify particular features of 2D spectra by a vector projection operation to simplify their interpretation. Concatenated 2D correlation [8b, 8c] is a sensitive tool to detect deviation from reversible process. Moving window analyses [8d, 8f] provide the visual representation of spectral intensity variation patterns along the perturbation axis. They are especially useful in choosing the region of interest along the perturbation axis for the subsequent detailed 2D correlation analysis. Determination of sequential order of spectral intensity variations is an important topic in the field of 2D correlation spectroscopy [8g]. 2D codistribution analysis [8h] is a newly introduced tool useful for determining the sequential order of presence of species in a dynamic reaction process.
Sample-sample correlation [8i] brings out the similarity of spectra at different perturbation points. 2D correlation based on principal component analysis (PCA) combined with eigenvalue manipulation transformation [8j] is a powerful technique for noise reduction and feature enhancement. Peak position shift effect in 2D correlation analysis was investigated [8g, 8f]. Non-uniform increment sampling [8k] is sometimes necessary but rather straightforward. Pareto scaling [8l] is a useful technique to enhance subtle feature of 2D correlation spectra obscured by strong signals. Quadrature orthogonal signal correction [8m] focuses on the analysis on signals pertinent only to the perturbation variable. Coherence and global phase angles [8n, 8o] are semi-quantitative metrics generated from 2D correlation analysis. Kernel analysis [8p] represents 2D correlation spectra in terms of a compact matrix consisting of a few parameters.
4. Concluding remarks2D correlation spectroscopy has become a very popular tool in the field of analytical science due to its versatility and relative ease of use. The technique can be utilized with a number of spectroscopic and other analytical probes for a very broad range of sample systems by employing different types of external perturbations to induce spectral variations. In the recent years,a number of new types of 2D correlation spectroscopy techniques have been introduced. In this review,2D hetero-correlation and multiple perturbation correlation analyses,including orthogonal sample design scheme,were specifically discussed in detail. References to other important developments in the field of 2D correlation spectroscopy,such as projection correlation and codistribution analysis,were also provided.
| [1] | (a) I. Noda, Two-dimensional infrared (2D IR) spectroscopy of synthetic and biopolymers, Bull. Am. Phys. Soc. 31 (1986) 520; (b) I. Noda, Two-dimensional infrared (2D IR) spectroscopy, J. Am. Chem. Soc. 111 (1989) 8116-8120; (c) I. Noda, Two-dimensional infrared (2D IR) spectroscopy: theory and applications, Appl. Spectrosc. 44 (1990) 550-561; (d) I. Noda, Generalized two-dimensional correlation method applicable to infrared, Raman, and other types of spectroscopy, Appl. Spectrosc. 47 (1993) 1329-1336; (e) I. Noda, Determination of two-dimensional correlation spectra using the Hilbert transform, Appl. Spectrosc. 54 (2000) 994-999; (f) I. Noda, A.E. Dowrey, C. Marcott, G.M. Story, Y. Ozaki, Generalized two-dimensional correlation spectroscopy, Appl. Spectrosc. 54 (2000) 236A-248A; (g) I. Noda, Y. Ozaki, Two-dimensional Correlation Spectroscopy—Applications in Vibrational and Optical Spectroscopy, Wiley, Chichester, 2004. |
| [2] | (a) I. Noda, A.E. Dowrey, C. Marcott, Recent developments in two-dimensional infrared (2D IR) correlation spectroscopy, Appl. Spectrosc. 47 (1993) 1317-1323; (b) I. Noda, Progress in 2D correlation spectroscopy, in: Y. Ozaki, I. Noda (Eds.), Two-Dimensional Correlation Spectroscopy, AIP Press, Melville, 2000, pp. 3-17; (c) I. Noda, Advances in two-dimensional correlation spectroscopy, Viv. Spectrosc. 36 (2004) 143-165; (d) I. Noda, Progress in two-dimensional (2D) correlation spectroscopy, J. Mol. Struct. 799 (2006) 2-15; (e) I. Noda, Recent advancement in the field of two-dimensional correlation spectroscopy, J. Mol. Struct. 883-884 (2008) 2-26; (f) I. Noda, Two-dimensional correlation spectroscopy—biannual survey 2007-2009, J. Mol. Struct. 974 (2010) 3-24; (g) I. Noda, Frontiers of two-dimensional correlation spectroscopy. Part 1. New concepts and noteworthy developments, J. Mol. Struct. 1069 (2014) 3-22; (h) I. Noda, Frontiers of two-dimensional correlation spectroscopy. Part 2. Perturbation methods, fields of applications, and types of analytical probes, J. Mol. Struct. 1069 (2014) 23-49. |
| [3] | (a) I. Noda, Two-dimensional correlation approach to the dynamic rheooptical characterization of polymers, Chemtracts Macromol. Chem. 1 (1990) 89-105; (b) F.E. Barton II, D.S. Himmersbach, J.H. Duckworth, M.J. Smith, Two-dimensional vibrational spectroscopy: correlation of mid-and near-infrared regions, Appl. Spectrosc. 46 (1992) 420-429; (c) N. Katayama, M. Kondo, M. Miyazawa, Study on molecular structure and hydration mechanism of Domyouji-ko starch by IE and NIR hetero 2D analysis, J. Mol. Struct. 974 (2010) 179-182; (d) T. Nishi, T. Genkawa, M. Watari, Y. Ozaki, Selection of NIR region for a regression model of the ethanol concentration in fermentation process by an online NIR and mid-IR dual-region spectrometer and 2D heterospectral correlation spectroscopy, Anal. Sci. 28 (2012) 1165-1170; (e) H. Yamasaki, S. Morita, Epoxy curing reaction studied by using two-dimensional correlation infrared and near-infrared spectroscopy, J. Appl. Polym. Sci. 119 (2011) 871-881; (f) B.K. Via, S. Adhikari, S. Taylor, Modeling for proximate analysis and heating value of torrefied biomass with vibrational spectroscopy, Bioresour. Technol. 133 (2013) 1-8;(g) Ž. Sovová, V. Kopecký Jr., T. Pazderka, et al., Structural analysis of natural killer cell receptor protein 1 (NKR-P1) extracellular domains suggests a conserved long loop region involved in ligand specificity, J. Mol. Model. 17 (2011) 1353-1370; (h) T.R. Rudd, E.A. Yates, M. Hricovíni, Spectroscopic and theoretical approaches for the determination of heparin saccharide structure and the study of protein-glycosaminoglycan complexes in solution, Curr. Med. Chem. 16 (2009) 4750-4766; (i) H.C. Choi, S.R. Ryu, H. Ji, et al., Two-dimensional hetero-spectral correlation analysis of X-ray photoelectron spectra and infrared spectra for spin-coated films of biodegradable poly(3-hydroxubutyrate-co-3-hydroxyhexanoate) copolymers, J. Phys. Chem. B 114 (2010) 10979-10985; (j) M. Mecozzi, M. Pietroletti, V. Gallo, M.E. Conti, Formation of incubated marine mucilages investigated by FTIR and UV-vis spectroscopy and supported by twodimensional correlation analysis, Marine Chem. 116 (2009) 18-35; (k) S.R. Ryu, W.M. Bae, W.J. Hong, K.J. Ihn, Y.M. Jung, Characterization of chain transfer reaction during radical polymerization of silver nanocomposite polyvinylpyrrolidone by using 2D hetero-spectral IR/NMR correlation spectroscopy, Vib. Spectrosc. 60 (2012) 168-172; (l) D.S. Smirnova, J.A. Kornfield, D.J. Lohshe, Morphology development in model polyethylene via two-dimensional correlation analysis, Macromolecules 44 (2011) 6836-6848; (m) L. Guo, N. Spegazzini, H. Sato, et al., Multistep crystallization process involving sequential formations of density fluctuations, “intermediate structures”, and lamellar crystallites: poly(3-hydroxybutyrate) as investigated by time-resolved synchrotron SAXS and WAXD, Macromolecules 45 (2012) 313-328; (n) L.R. Whitman, K.P. Bork, Y. Tang, Two-dimensional correlation in cyclic voltammetry and electrochemical quartz crystal microbalance: a complementary tool to conventional techniques, J. Electroanal. Chem. 661 (2011) 100-105; (o) J. Andary, J. Maalouly, R. Quaini, et al., Application of 2D correlation spectroscopy on olive stones acid hydrolysates: effect of overliming, Chemom. Intell. Lab. Syst. 113 (2012) 58-67. |
| [4] | (a) L.T. Letendre, W. McNavage, C. Pibel, D.K. Kuo, H.L. Dai, Time-resolved FTIR emission spectroscopy of transient radicals, J. Chin. Chem. Soc. 52 (2005) 677-686; (b) W. McNavage, H.L. Dai, Two-dimensional cross-spectral correlation analysis and its application to time-resolved Fourier transform emission spectra of transient radicals, J. Chem. Phys. 123 (2005) 184104; (c) F. Pi, H. Shinzawa, M.A. Czarnecki, M. Iwahashi, M. Suzuki, Y. Ozaki, Selfassembling of oleic acid (cis-9,cis-12-octadecalienoic acid) in ethanol studied by time-dependent attenuated total reflectance (ATR) infrared (IR) and two-dimensional (2D) correlation spectroscopy, J. Mol. Struct. 974 (2010) 40-45; (d) C. Marcott, G.M. Story, A.E. Dowrey, I. Noda, in: C.L. Wilkins (Ed.), Enhancement of Chemical Information through Computer-Assisted Examination of Spectral Variations, vol. 4, Computer-Enhanced Analytical Spectroscopy, Plenum, New York, 1993, pp. 237-255; (e) J. Xu, S. Cai, X. Li, J. Dong, J. Ding, Z. Chen, Statistical two-dimensional correlation spectroscopy of urine and serum from metabolomics data, Chemom. Intell. Lab. Syst. 112 (2012) 33-40. |
| [5] | (a) Y. Wu, J.H. Jiang, Y. Ozaki, A new possibility of generalized two-dimensional correlation spectroscopy: hybrid two-dimensional correlation spectroscopy, J. Phys. Chem. A 106 (2002) 2422-2429; (b) Y. Wu, F. Meersman, Y. Ozaki, A novel application of hybrid two-dimensional correlation infrared spectroscopy: exploration of the reversibility of the pressureand temperature-induced phase separation of poly(N-isopropylacrylamide) and poly(N-isopropylmethacrylamide) in aqueous solution, Macromolecules 39 (2006) 1182-1188; (c) T.J. Kamerzell, C.R. Middaugh, Two-dimensional correlation spectroscopy reveals coupled immunoglobulin regions of differential flexibility that influence stability, Biochemistry 46 (2007) 9762-9773; (d) G.M. Kirwan, D.I. Fernandez, J.O. Niere, M.J. Adams, General and hybrid correlation nuclear magnetic resonance analysis of phosphorous in Phytophthora palmivora, Anal. Biochem. 429 (2012) 1-7; (e) W. Zhang, R. Liu, W. Zhang, H. Jia, K. Xu, Discussion on the validity of NIR spectral data in non-invasive blood glucose sensing, Biomed. Opt. Expr. 4 (2013) 789-803. |
| [6] | (a) H. Shinzawa, K. Awa, T. Okumura, S. Morita, M. Otsuka, Y. Ozaki, H. Sato, Raman imaging analysis of pharmaceutical tablets by two-dimensional (2D) correlation spectroscopy, Vib. Spectrosc. 51 (2009) 125-131; (b) H. Shinzawa, S. Morita, K. Awa, et al., Multiple perturbation two-dimensional correlation analysis of cellulose by attenuated total reflection infrared spectroscopy, Appl. Spectrosc. 63 (2009) 501-506; (c) H. Shinzawa, T. Genkawa, W. Kanematsu, Pressure-induced association of oleic acid (OA) under varying temperature studied by multiple-perturbation two-dimensional (2D) IR correlation spectroscopy, J. Mol. Struct. 1028 (2012) 164-169; (d) H. Shinzawa, M. Nishida, W. Kanematsu, et al., Parallel factor (PARAFAC) kernel analysis of temperature-and composition-dependent NMR spectra of poly(lactic acid) nanocomposites, Analyst 137 (2012) 1913-1921; (e) H. Shinzawa, K. Awa, I. Noda, Y. Ozaki, Multiple-perturbation two-dimensional near-infrared correlation study of time-dependent water absorption behavior of cellulose affected by pressure, Appl. Spectrosc. 67 (2013) 163-170. |
| [7] | (a) J. Qi, H. Li, K. Huang, et al., Orthogonal sample design scheme for twodimensional synchronous spectroscopy and its application in probing intermolecular interactions, Appl. Spectrosc. 61 (2007) 1359-1365; (b) J. Qi, K. Huang, X. Gao, et al., Orthogonal sample design scheme for twodimensional synchronous spectroscopy: application in probing lanthanide ions interactions with organic ligands in solution mixture, J. Mol. Struct. 883-884 (2008) 116-123; (c) Y. Liu, C. Zhang, S. Liu, et al., Modified orthogonal sample design scheme to probe intermolecular interactions, J. Mol. Struct. 883-884 (2008) 124-128; (d) C. Zhang, K. Huang, H. Li, et al., Double orthogonal sample design scheme and corresponding basic patterns in two-dimensional correlation spectra for probing subtle spectral variations caused by intermolecular interactions, J. Phys. Chem. A 113 (2009) 12142-12156; (e) X. Li, Q. Pan, J. Chen, et al., Asynchronous orthogonal sample design scheme for two-dimensional correlation spectroscopy (2D-COS) and its application in probing intermolecular interactions from overlapping infrared (IR) bands, Appl. Spectrosc. 65 (2011) 901-917; (f) J. Chen, Q. Bi, S. Liu, et al., Double asynchronous sample design scheme for probing intermolecular interactions, J. Phys. Chem. A 116 (2012) 10904-10916; (g) X. Li, S. Liu, J. Chen, et al., The influence of changing the sequence of concentration series on the 2D asynchronous spectroscopy generated by the asynchronous orthogonal sample design (AOSD) approach, Vib. Spectrosc. 60 (2012) 212-216; (h) X. Li, Q. Bi, S. Liu, et al., Improvement of the sensitivity of the twodimensional asynchronous spectroscopy based on the ASOD approach by using a modified reference spectrum, J. Mol. Struct. 1034 (2013) 101-111. |
| [8] | (a) I. Noda, Projection two-dimensional correlation analysis, J. Mol. Struct. 974 (2010) 116-126; (b) L. Zhang, I. Noda, Y. Wu, Concatenated two-dimensional correlation analysis: a new possibility for generalized two-dimensional correlation spectroscopy and its application to the examination of process reversibility, Appl. Spectrosc. 64 (2010) 343-350; (c) L. Zhang, I. Noda, Y. Wu, An application of concatenated 2D correlation spectroscopy: exploration of the reversibility of the temperature-induced hydration variation of poly(N-isopropylmethacrylamide) in aqueous solution, J. Mol. Struct. 974 (2010) 80-87; (d) M. Thomas, H. Richardson, Two-dimensional FT-IR correlation analysis of the phase transitions in a liquid crystal 40-n-octyl-cyanobiphenyl (8CB), Vib. Spectrosc. 24 (2000) 137-146; (e) S. Morita, H. Shinzawa, I. Noda, Y. Ozaki, Perturbation-correlation movingwindow two-dimensional correlation spectroscopy, Appl. Spectrosc. 60 (2006) 398-406; (f) S.R. Ryu, I. Noda, C.H. Lee, et al., Two-dimensional correlation analysis and waterfall plots for detecting positional fluctuations of spectral changes, Appl. Spectrosc. 65 (2011) 359-368; (g) I. Noda, Close-up view on the inner workings of two-dimensional correlation spectroscopy, Vib. Spectrosc. 60 (2012) 146-153; (h) I. Noda, Two-dimensional codistribution spectroscopy to determine the sequential order of distributed presence of species, J. Mol. Struct. 1069 (2014) 60-72; (i) S. Š ašić, A. Muszynski, Y. Ozaki, A new possibility of the generalized twodimensional correlation spectroscopy. 1. Sample-sample correlation spectroscopy, J. Phys. Chem. A 104 (2000) 6380-6387; (j) Y.M. Jung, S.B. Kim, I. Noda, New approach to generalized two-dimensional correlation spectroscopy. II: Eigenvalue manipulation transformation (EMT) for noise suppression, Appl. Spectrosc. 57 (2003) 557-563; (k) I. Noda, Two-dimensional correlation analysis of unevenly spaced spectral data, Appl. Spectrosc. 57 (2003) 1049-1051; (l) I. Noda, Scaling techniques to enhance two-dimensional correlation spectra, J. Mol. Struct. 883-884 (2008) 216-227; (m) Y. Wu, I. Noda, Extension of quadrature orthogonal signal corrected twodimensional (QOSC 2D) correlation spectroscopy I: principal component analysis based QOSC 2D, Appl. Spectrosc. 61 (2007) 1040-1044; (m) I. Noda, Recent mathematical developments in 2D correlation spectroscopy, in: Y. Ozaki, I. Noda (Eds.), Two-Dimensional Correlation Spectroscopy, AIP Press, Melville, 2000, pp. 201-204; (o) S. Morita, Y. Ozaki, I. Noda, Global phase angle description of generalized twodimensional correlation spectroscopy: 1. theory and its simulation for practical use, Appl. Spectrosc. 55 (2001) 1618-1621; (p) I. Noda, Kernel analysis for two-dimensional (2D) correlation spectroscopy, J. Mol. Struct. 799 (2006) 34-40. |




