Polymers in solution exposed to shear flow exhibit large conformational changes due to tumbling motion,i.e.,they stretch and collapse with a characteristic frequency depending on shear rate. This behavior has intensively been studied experimentally and numerically [1, 2, 3, 4, 5, 6, 7]. In contrast,the flow-induced dynamical behavior of polymers absorbed on a surface has received far less attention [8]. Insight into the behavior of such systems is of fundamental importance in a wide spectrum of systems ranging from the separation of macromolecules using microcircuit devices to the gene therapy in which DNA is transported to a desired target site [9, 10, 11, 12, 13].
The dynamic behavior of an absorbed polymer in shear flow is governed by various parameters; aside from the shear rate,the properties of surfaces are of major importance. Since the tumbling dynamics is usually observed at high shear rates close to the critical shear rate at which chains desorb,hydrodynamic interactions (HI) are also believed to play an important role in this behavior.
In this letter,we investigate the tumbling dynamics of individual absorbed polymers by a hybrid mesoscale simulation approach,which combining molecular dynamics for the polymer molecules with the multiparticle collision dynamics describing the solvent [14]. As has been shown,this hybrid method is very well suited to study the properties of polymer solutions,where both thermal fluctuations and hydrodynamics are important [15, 16].
2. ExperimentalIn our model,a flexible polymer chain in an explicit solvent consistsofN = 20monomersofmassMeach.Theexcluded-volume interactions between monomers are described by the truncated- shift purely repulsive Lennard-Jones (LJ) potential with the parameter s characterizing the monomer size and e the energy. A finite extensible nonlinear elastic potential (FENE),with the maximum bond length 1.5 s and the spring constant 30 e/s2,is used to model the connectivity between adjacent monomers of the chain. The monomer dynamics is determined by Newton’s equations of motion,which are integrated by the velocity Verlet algorithm with time step hp. The multiparticle collision dynamics method is used to describe the solvent. It is composed of Nspoint- like particles of mass m. The algorithm consists of alternating streaming and collision steps. In the streaming step,the solvent particles move ballistically for a time h. In the collision steps, particles are sorted into cubic cells of side length and their relative velocities,with respect to the center-of-mass velocity of their cell, are rotated around a randomly oriented axis by a fixed anglea. The solvent-polymer coupling is achieved by taking the monomers into account in the collision step. The system is confined between two parallel walls as shown in Fig. 1. Shear flow is imposed by sliding the upper wall relative to the lower wall at a constant rate and periodic boundary conditions are applied parallel to the walls.We impose no-slip boundary conditions at walls for solvent particles. The chain is absorbed on the lower wall by the LJ potential with the interaction strength εw and the cutoff distance 2.5 s,Uadsorb. Two types of walls are considered. The first is a smoothsurface for monomers; the second is atomically corrugated and the interactions between monomers and the surface are U = Uadsorb [1 + A cos(2px/q) sin(2py/q)] with q = 1 and A = 0.2 consistent with previous works [17]. The energy of interaction of the chain with the lower wall includes repulsive and attractive parts,the attractivepart makesthechainadsorb onthesurfaceand the repulsive part avoids monomer moving outside the wall. Periodic boundary conditions are applied in the directions parallel to the walls. The shear flow with shear rate = Vwall/Lz is introduced into the system by the motion of the upper wall and bounce-back boundary condition being applied simultaneously,which means the solvent particles reverse their direction of velocity butkeep the magnitude constant. The system is in the canonical ensemble (NVT) and the viscous friction of particles with the walls of the simulation box creates heat that result in temperature rising, which can influence the velocity of particles,therefore thermo- stattingisrequiredinthenonequilibriumMPCDsimulation.Alocal Maxwellian thermostat is used to keep the temperature at the desired value [18].

|
Download:
|
| Fig. 1. Schematic depiction of an absorbed polymer chain under shear flow. | |
All simulations are performed with σ = ε = α = 1,α = 1308,the average number of solvent particles per cell ρ = 10,M = rm, h = 0.1s(m/kBT)1/2 (where kB is the Boltzmann constant and T the temperature),hp/h = 20,m = 1,and kBT = 1. A simulation box with size 30 × 20 × 20 is applied. More than 50 parallel samples with different initial conditions for each data to improve the quality of the results.
3. Results and discussionWhen polymer fluids are subjected to a simple shear flow,the
velocity across the chain is substantial,and hence it may undergo
large conformational changes; i.e.,a polymer chain stretches and
recoilsinthecourseoftime[1, 2, 3, 4, 5].Theinstantaneousconformation
of polymers can be quantitatively characterized by the gyration
tensor,which is defined as Gab¼PN
i¼1Dri;aDri;b=N,where Dri,ais
the position of monomer i in the center of mass reference frame of
the polymer anda,b 2 x,y,z denote Cartesian components[16]. The
average gyration tensor is denoted as 〈Gαβ〉,where h?i denotes
ensemble average. It is noticed that Gabcan be directly accessed in
single molecule experiments and 〈Gαβ〉 in scattering experiments.
At infinite dilution,the flow strength is characterized by the
Weissenberg number Wi ¼ ![]() · t,where
· t,where ![]() is the shear rate and t0
the longest relaxation time obtained at equilibrium.
is the shear rate and t0
the longest relaxation time obtained at equilibrium.
The tumbling dynamics of polymers absorbed on surfaces is observed for Wi ? 1 where the chains are not able to relax back to the equilibrium conformation. The time traces of relative deformation of chains along the flow and gradient directions are shown in Fig. 2. It is clear that in the tumbling process,the extension of a chain along the flow direction always follows the shrinkage of its gradient thickness,or a chain stretching along the gradient direction follows the retraction in the flow direction. Furthermore,the maximum extension in the flow (gradient) direction always relates to the shrinkage in the gradient (flow) direction.
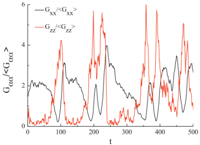
|
Download:
|
| Fig. 2. Time trajectories of the extensions of the radius of gyration along the flow and gradient directions for Wi = 617.7 with εw= 4.0. | |
In order to obtain the characteristic time for the tumbling dynamics,we determine the cross-correlation function between the conformational changes in flow and gradient directions, calculated as [3, 6, 15, 19]
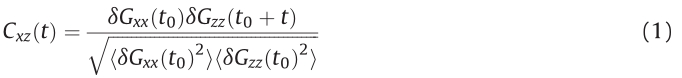
Here δGaa= Gaa? hGaai. Fig. 3 shows cross-correlation func- tions for several Weissenberg numbers for εw= 4.0. Similarly to unconstrained linear polymers, the tumbling dynamics of absorbed polymers is not perfectly periodic because the autocor- relation,Cxz,decays to zero at large time-lags. Cxzexhibits the maximum at t?,indicating that positive values of dGxx are correlated with positive values dGzz,or a collapsed state along the x-direction is correlated with a previous collapsed sated in y-direction. The minimum of Cxzat t+reveals that positive values of dGaaare linked with negative ones of the orthogonal directions;i.e.,polymer compresses in the z-direction is linked with its extension in x-direction. Hence,the difference t+? t?is related to conformational changes of polymers due to tumbling. Here,the characteristicoftumblingmotionisdefinedastt= 2(t+? t?),where the factor two is attributed to two non-equivalent conformations leading to a maximum and a minimum,respectively.

|
Download:
|
| Fig. 3. Cross-correlation functions for a polymer absorbed on the smooth surface with εw= 4.0 for various Weissenberg numbers as indicated. | |
Normalized tumbling frequencies ft= t0/tt,scaled by the relaxation time t0,as a function of the Weissenberg number are shown in Fig. 4. Data for various absorption strengthscollapse onto a universal curve,which can be described by a power law ft? Wim with m = 0.80. Lo¨wen and his co-workers reported a larger exponent m = 0.90 obtained by Brownian dynamics simulations [8]. In their work,the characteristic time is calculated from the Fourier transform of the autocorrelation of the radius of gyration [8]. However,Delgado-Buscalionipointedout that the morenature measure of the tumbling motion is the cross correlation between the chain extension along flow and gradient directions,namely, Eq. (1) [19]. This scaling behavioris practically consistent with that of a polymer with one end tethered on a surface,for which ft? Wi0.78is observed [19]. For unconstrained individual polymers in dilute solution,a somewhat smaller exponent m = 0.67 was obtained in Refs. [2, 3, 6]. Furthermore,Fig. 4 also shows that the corrugation of surfaces has no effect on the shear dependence of ft.

|
Download:
|
| Fig. 4. The normalized tumbling frequencies ft,scaled withtherelaxationtimet0for various ewas indicated. | |
In summary,we study the tumbling dynamics of individual absorbed polymer chains in shear flow. The cross-correlation betweenthechainextensionalongflowandgradientdirectionsare used to characterize the tumbling motion. The results show that the normalized tumbling frequencies follow the power law ft ≈ Wi0.80. We find that both adsorptive strength and surface corrugation have no influence on the scaling behavior of tumbling dynamics.
AcknowledgmentsThis work is supported by the National Natural Science FoundationofChina(No.21274153).WearegratefultoComputing Center of Jilin Province for essential support.
| [1] | S. Gerashchenko, V. Steinberg, Statistics of tumbling of a single polymer molecule in shear flow, Phys. Rev. Lett. 96 (2006) 038304. |
| [2] | C.M. Schroeder, R.E. Teixeira, E.S.G. Shaqfeh, S. Chu, Characteristic periodic motion of polymers in shear flow, Phys. Rev. Lett. 95 (2005) 018301. |
| [3] | C.C. Huang, G. Sutmann, G. Gompper, Tumbling of polymers in semidilute solution under shear flow, Europhys. Lett. 93 (2011) 54004. |
| [4] | C. Aust, S. Hess, M. Kröer, Rotation and deformation of a finitely extendable flexible polymer molecule in a steady shear flow, Macromolecules 35 (2002) 8621-8630. |
| [5] | S. Liu, B. Ashok, M. Muthukumar, Brownian dynamics simulations of bead-rodchain simple shear flow and elongational flow, Polymer 45 (2004) 1383-1389. |
| [6] | R.E. Teixeira, H.P. Babcock, E.S.G. Shaqfeh, S. Chu, Shear thinning and tumbling dynamics of single polymers in the flow-gradient plane, Macromolecules 38 (2005) 581-592. |
| [7] | C.M. Schroeder, R.E. Teixeira, E.S.G. Shaqfeh, S. Chu, Dynamics of DNA in the flowgradient plane of steady shear flow: observations and simulations, Macromolecules 38 (2005) 1967-1978. |
| [8] | G.L. He, R. Messina, H. Löwen, Statistics of polymer adsorption under shear flow, J. Chem. Phys. 132 (2010) 124903. |
| [9] | B.D. Ratner, S.J. Bryant, Biomaterials: where we have been and where we are going, Annu. Rev. Biomed. Eng. 6 (2004) 41-75. |
| [10] | F. Rusmini, Z.Y. Zhong, J. Feijen, Protein immobilization strategies for protein biochips, Biomacromolecules 8 (2007) 1775-1789. |
| [11] | M. Chopra, R.G. Larson, Brownian dynamics simulations of isolated polymer molecules in shear flow near adsorbing and nonadsorbing surfaces, J. Rheol. 46 (2002) 831-862. |
| [12] | C. Zhang, J. Xu, W. Ma, W. Zheng, PCR microfluidic devices for DNA amplification, Biotechnol. Adv. 24 (2006) 243-284. |
| [13] | M. Hashimoto, F. Barany, S.A. Soper, Polymerase chain reaction/ligase detection reaction/hybridization assays using flow-through microfluidic devices for the detection of low-abundant DNA point mutations, Biosens. Bioelectron. 21 (2006) 1915-1923. |
| [14] | A. Malevanets, R. Kapral, Mesoscopic model for solvent dynamics, J. Chem. Phys. 110 (1999) 8605-8613. |
| [15] | W.D. Chen, J.Z. Chen, L.J. An, Tumbling and tank-treading dynamics of individual ring polymers in shear flow, Soft Matter 9 (2013) 4312-4318. |
| [16] | W.D. Chen, J.Z. Chen, L.J. Liu, X.L. Xu, L.J. An, Effects of chain stiffness on conformational and dynamical properties of individual ring polymers in shear flow, Macromolecules 46 (2013) 7542-7549. |
| [17] | T.G. Desai, P. Keblinski, S.K. Kumar, S. Granick, Modeling diffusion of adsorbed polymer with explicit solvent, Phys. Rev. Lett. 98 (2007) 218301. |
| [18] | C.C. Huang, A. Chatterji, G. Sutmann, G. Gompper, R.G. Winkler, Cell-level canonical sampling by velocity scaling for multiparticle collision dynamics simulations, J. Comput. Phys. 229 (2010) 168-177. |
| [19] | R. Delgado-Buscalioni, Cyclic motion of a grafted polymer under shear flow, Phys. Rev. Lett. 96 (2006) 088303. |




