2. 中国人民解放军 93811部队86分队, 兰州 730020;
3. 中国气象局兰州干旱气象研究所, 甘肃省干旱气候变化与减灾重点实验室, 中国气象局干旱气候变化与减灾重点开放实验室, 兰州 730020;
4. 中国气象局数值预报中心, 北京 100081;
5. 中国气象科学研究院灾害天气国家重点实验室, 北京 100081;
6. 中国人民解放军 95920部队气象台, 衡水 253801
2. Unit 86 of No. 93811 PLA, Lanzhou 730020;
3. Key Laboratory of Arid Climatic Change and Reducing Disaster of Gansu Province, Key Open Laboratory of Arid Climatic Change and Disaster Reduction of CMA, Institute of Arid Meteorology, CMA, Lanzhou 730020;
4. Center for Numerical Prediction, China Meteorological Administration, Beijing 100081;
5. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081;
6. Meteorological Observatory of No. 95920 PLA, Hengshui 253801
数值预报是以大气运动方程组为骨架,加入了各种物理过程和参数化方案的模式预报系统,是对真实大气运动的近似描述[1-2]。由于大气是一个连续、复杂的混沌系统[3],具有非线性特征[4],而数值模式只能描述真实大气运动的有限过程,因此,不可避免地会产生模式误差[5-7]。数值模式的预报误差来源可以分为系统误差和非系统误差两大类[8-9],系统误差主要反映模式对于实际气候态的漂移程度,一般是模式自身的缺陷所致,可以通过系统订正的方法有效减少[10]。而非系统误差是依赖于大气状态变量的预报误差,其主要来源有两个:一是初始误差场的非线性增长,二是模式本身的缺陷[11]。研究表明:系统误差约占总误差的20%,而非系统误差则占总误差的80%左右[8]。对于系统误差来讲,模式模拟误差的大小与所选取的样本量密切相关,误差会随着样本量的增加不断减小,但对于非系统误差,样本的选取比样本量的增加更为重要[12-13]。因此,非系统误差的订正重要性更强、订正难度也更大。
非系统误差对总误差的贡献巨大,随着预报时效的增长,预报场与真实大气的偏离程度在很大程度上反映在非系统误差的增长速率上,而这种偏离与预报时效内出现的复杂天气现象密不可分。因此,系统深入地研究非系统误差,分析其时空演变规律,有助于剖析所发生天气过程的内在物理机制,加深对复杂天气预报误差的理解[14]。
全球/区域一体化同化预报系统GRAPES(Global/Regional Assimilation and Prediction System)是我国自主研发的多尺度通用资料同化和数值预报系统。经过对模式物理过程的完善、三维变分同化系统的改进和卫星资料同化应用的补充[15-16],GRAPES_GFS 2.0于2016年正式投入业务应用。对GRAPES_GFS 2.0模式系统误差评估发现,误差大值集中在中高纬度地区且在南、北半球各自的冬季最大、夏季最小,并呈明显季节变化特征[17]。本文则以非系统误差为研究对象。
本文将利用经验正交函数分解等预报诊断方法[18],对各等压面、不同预报时效下的非系统误差进行详细评估,寻找GRAPES_GFS 2.0非系统误差的普遍规律。本研究中,所选取试验时间指2014年具有季节代表性的1月、4月、7月、10月。
1 资料与方法本文采用GRAPES_GFS 2.0进行数值模拟,利用地基和探空观测资料及卫星遥感资料并通过三维变分同化得到的位势高度场、温度场和风场作为初始场;以全可压、非静力平衡的动力方程组作为模式动力框架,利用两时间层半隐式-半拉格朗日方法进行时空离散化;水平方向为Arakawa-C交错网格分布的全球经纬网格模式、垂直方向为Charney-Phillips分层设置[16],采用高度地形追随坐标,垂直分层为非均匀分层,模式低层的垂直层间隔较密、垂直层厚度可调。对于物理过程,辐射方案选用RR- TMG LW(V4.71)/SW(V3.61)方案[19],陆面过程选用通用陆面模式CoLM[20-21],微物理过程选用CMA双参数方案,积云对流参数化方案则是简化的Arakawa-Schubert(SAS)方案[22],使用了基于双参数云物理方案的micro-cloud方案,引入了次网格尺度地形重力波参数化[23-25]。
本文选取了GRAPES_GFS 2.0模式预报所选取试验时间的资料,与对应时刻NCEP FNL分析资料进行对比。预报初始场采用的是GRAPES模式本身的每6 h输出1次的同化循环产品,积分时间为8 d,每6 h输出1次预报结果,水平分辨率为0.25°×0.25°。
位势高度、温度和纬向风是主要数值预报产品,本文主要对这3种产品的非系统误差进行评估。为区分系统误差和非系统误差,这里将预报场和分析场分解为平均态和扰动态,预报场平均态是指GRAPES_GFS 2.0模式所选取试验时间每月样本在同一预报时刻的平均值,分析场的平均态是指所选取试验时间每月对应预报时刻NCEP FNL分析资料平均值。将预报场的平均态记为 
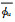
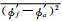
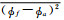
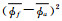

|
(1) |
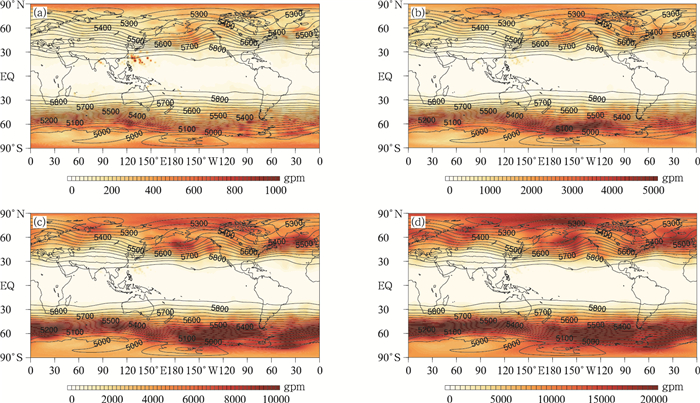
500 hPa位势高度场平均非系统误差可以表征对流层中部位势高度场误差的平均状态,具有很好的代表性。由图 1可知,北半球全年平均位势高度场基本呈弱的两槽两脊型分布态势,槽区位于北太平洋和北大西洋地区,脊区位于欧亚大陆和北美大陆。由于南半球中纬度地区下垫面相对均一平坦,因此,等位势高度线在南半球较为平直。从非系统误差的空间分布情况看,北半球的误差大值主要分布在北太平洋和北大西洋,南半球则以中纬度等位势高度线密集区为中心呈条带状分布,大体与西风急流带重合。总体上,误差大值集中在中高纬度地区,低纬度地区误差相对较小。这可能是由于中高纬度地区斜压性较强、非系统误差易增长,GRA- PES_GFS 2.0模式本身缺陷是造成非系统误差的部分原因[26-27]。从误差随时间变化看,误差大值区域基本不随预报时效增长发生变化,而误差增速明显大于线性增速。
|
|
| 图1 所选取试验时间平均的GRAPES_GFS 2.0模式预报时效为1 d(a), 3 d(b), 5 d(c), 8 d(d)时500 hPa位势高度场非系统误差(填色) (实线为NCEP FNL分析资料对应的平均场,单位:gpm) Fig.1 Forecast unsystematic errors of 500 hPa geopotential height field by GRAPES_GFS 2.0 with lead time of 1 d(a), 3 d(b), 5 d(c), 8 d(d) based on the average of selected time(the shaded) (solid lines denote mean field by NCEP FNL, unit:gpm) | |
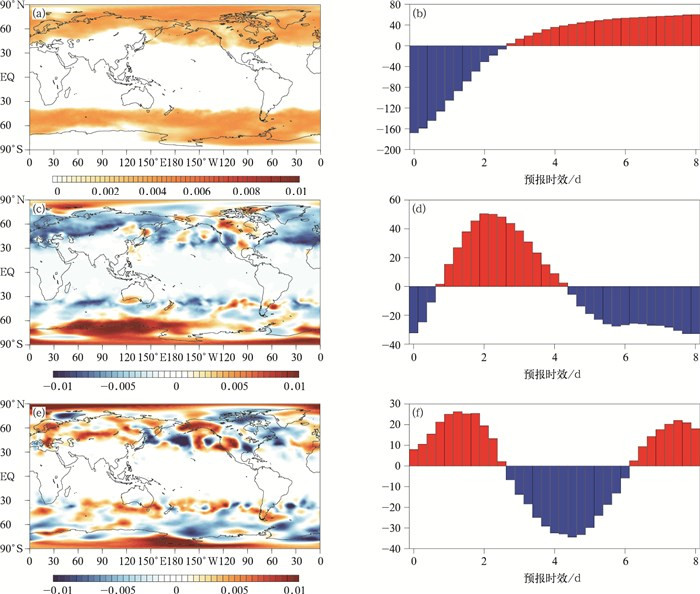
经验正交函数分解能够将随时间变化的变量场分解为不随时间变化的空间函数部分以及只依赖于时间变化的时间函数部分,可以将原场的主要信息浓缩在几个主要分量上,并通过该结果解释原场的物理特征。图 2是对500 hPa位势高度场非系统误差进行标准化后得到的经验正交函数分解前3个模态的空间分布和时间演变情况。前3个模态分别占总解释方差的65.4%,13.0%和6.2%,方差累积量占总解释方差的84.6%。第1空间模态偏离典型态的大值区主要集中在中高纬度地区,这与图 1所得结果互相印证;第1空间模态对应的时间系数呈单调上升趋势,上升速率先快后慢。第2空间模态中南、北半球中高纬度地区偏离典型场的方向相反,南半球中高纬度地区为正位相偏离,北半球则为负位相偏离;第2空间模态对应的时间系数呈正弦曲线变化,在预报时效约为2 d时出现极大值。第3空间模态正负位相交错,对应的时间系数也呈正弦曲线形式,周期约为6 d。
|
|
|
图2 所选取试验时间平均的500 hPa位势高度场非系统误差经验正交函数分解
(a)第1空间模态,(b)第1模态对应的时间系数,(c)第2空间模态,(d)第2模态对应的时间系数, (e)第3空间模态,(f)第3模态对应的时间系数 Fig.2 Empirical orthogonal function(EOF) analysis of unsystematic errors in 500 hPa geopotential height field based on the average of selected time (a)the first spatial mode, (b)the first mode corresponding to the time coefficient, (c)the second spatial mode, (d)the second mode corresponding to the time coefficient, (e)the third spatial mode, (f)the third mode corresponding to the time coefficient |
|
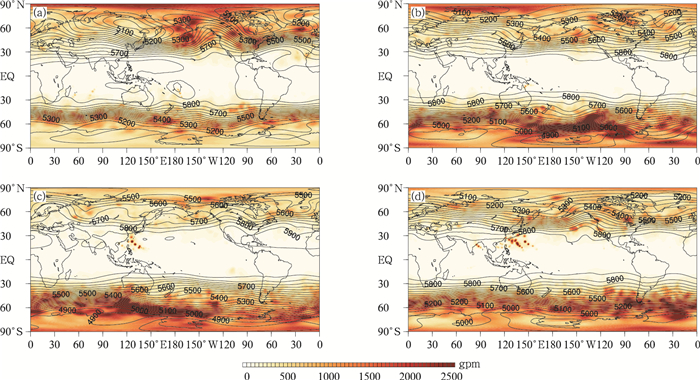
图 3为所选取试验时间500 hPa位势高度场预报时效为2 d时的平均非系统误差,代表了短时预报各季节非系统误差的空间分布状况。由图 2可以看到,4个季节的非系统误差大值都分布在中高纬度地区,与全年平均情况下的误差分布大体一致。南半球误差大值区域的面积更大、误差极值也更大,极大值位于南大洋区域,中心区随着季节的变化略有东西移动。北半球误差在1月达到极盛,大值位于白令海峡和北大西洋海域,与脊区基本重合。总体来说,可能是由于冬季位势高度的梯度最大,斜压性最强,因此,南、北半球的非系统误差面积和数值均为各自冬季最大、夏季最小,春、秋两季误差分布状况类似,介于冬季和夏季之间,呈过渡态。误差分布大致以1年为周期呈周期性变化。
|
|
|
图3 GRAPES_GFS 2.0模式预报时效为2 d时500 hPa位势高度场平均非系统误差(填色)
(实线为NCEP FNL分析资料对应的平均场,单位:gpm) (a)2014年1月,(b)2014年4月,(c)2014年7月,(d)2014年10月 Fig.3 Mean unsystematic errors(the shaded) of 500 hPa geopotential height field by GRAPES_GFS 2.0 with lead time of 2 days (solid lines denote mean field by NCEP FNL, unit:gpm) (a)January 2014, (b)April 2014, (c)July 2014, (d)October 2014 |
|
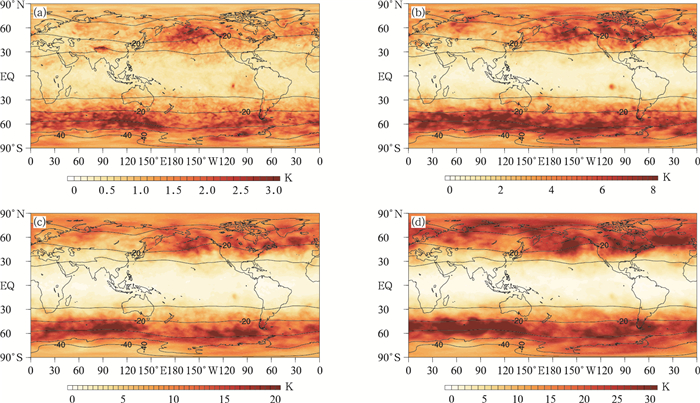
与位势高度相同,温度和纬向风也是业务预报中非常重要的气象要素。图 4~图 8为500 hPa温度场和200 hPa,850 hPa纬向风场及两者纬向平均场的误差分布和随预报时效的演变情况。与位势高度场类似,500 hPa温度场全年平均非系统误差的大值区也以中高纬度地区为主,南半球中纬度地区呈条带状均匀分布,北半球主要分布在白令海峡、北大西洋和二者中间的北美地区。误差空间分布的南、北半球差异较为明显。预报时效较短时,青藏高原地区误差较大,预报时效增加后,误差分布的海陆差异和地形差异变得并不显著,这可能是因为青藏高原地区初始场误差较大而增速较慢。误差随着预报时效的增加而增长,增速呈先快后慢的变化态势,这与位势高度场的误差增长曲线类似。
|
|
| 图4 所选取试验时间平均的GRAPES_GFS 2.0模式预报时效为1 d(a), 3 d(b), 5 d(c), 8 d(d)时500 hPa温度场的平均非系统误差(填色) (实线为NCEP FNL分析资料对应的平均场) Fig.4 Forecast unsystematic errors(the shaded) of 500 hPa temperature field by GRAPES_GFS 2.0 with the lead time of 1 day(a), 3 days(b), 5 days(c), 8 days(d) based on the average of selected time (solid lines denote mean field by NCEP FNL, unit:K) | |

|
|
| 图5 所选取试验时间平均的GRAPES_GFS 2.0模式预报时效为1 d(a),3 d(b),5 d(c),8 d(d)时纬向平均温度场的平均非系统误差(填色) (实线为NCEP FNL分析资料对应的平均场,单位:K) Fig.5 Forecast unsystematic errors(the shaded) in zonal average temperature field by GRAPES_GFS 2.0 with lead time of 1 day(a), 3 days(b), 5 days(c), 8 days(d) based on the average of selected time (solid lines denote mean field by NCEP FNL, unit:K) | |
|
|
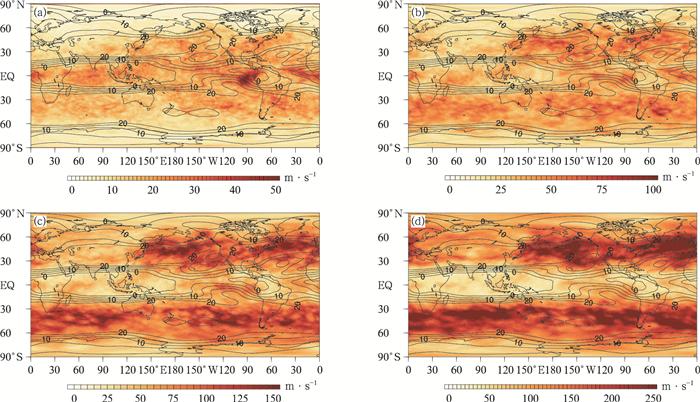
| 图6 所选取试验时间平均的GRAPES_GFS 2.0模式预报时效为1 d(a),3 d(b),5 d(c),8 d(d)时200 hPa纬向风场的平均非系统误差(填色) (实线为NCEP FNL分析资料对应的平均场,单位:m·s-1) Fig.6 Forecast unsystematic errors(the shaded) of 200 hPa zonal wind field by GRAPES_GFS 2.0 with lead time of 1 day(a), 3 days(b), 5 days(c), 8 days(d) based on the average of selected time (solid lines denote mean field by NCEP FNL, unit:m·s-1) | |
|
|
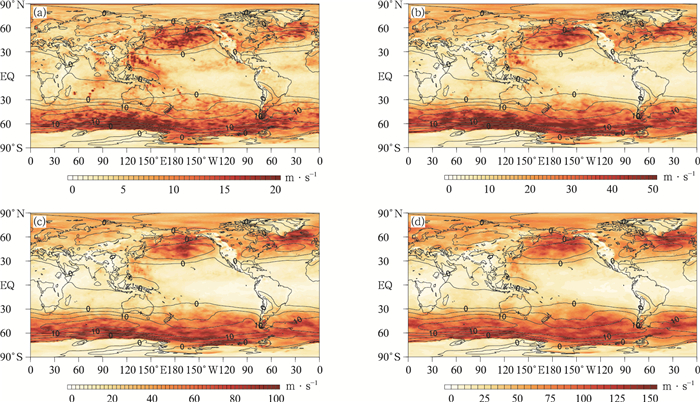
| 图7 所选取试验时间平均的GRAPES_GFS 2.0模式预报时效为1 d(a), 3 d(b), 5 d(c), 8 d(d)时850 hPa纬向风场的平均非系统误差(填色) (实线为NCEP FNL分析资料对应的平均场,单位:m·s-1) Fig.7 Forecast unsystematic errors(the shaded) of 850 hPa zonal wind field by GRAPES_GFS 2.0 with lead time of 1 day(a), 3 days(b), 5 days(c), 8 days(d) based on the average of selected time (solid lines denote mean field by NCEP FNL, unit:m·s-1) | |

|
|
| 图8 所选取试验时间平均的GRAPES_GFS 2.0模式预报时效为1 d(a), 3 d(b), 5 d(c), 8 d(d)时纬向平均风场的平均非系统误差(填色) (实线为NCEP FNL分析资料对应的平均场,单位:m·s-1) Fig.8 Forecast unsystematic errors(the shaded) of zonal average wind field by GRAPES_GFS 2.0 with lead time of 1 day(a), 3 days(b), 5 days(c), 8 days(d) based on the average of selected time (solid lines denote mean field by NCEP FNL, unit:m·s-1) | |
本文选择200~1000 hPa共16个等压面代表整个对流层和对流层与平流层交界面大约12 km高度(图 5)。纬向平均后发现,温度场非系统误差呈现出4个极大值区相互对称的空间分布特征,这与位势高度场的误差空间分布显著不同。4个极大值区分别位于50°~70°N和50°~70°S的200~300 hPa,500 hPa以下,以海洋为主的低纬度地区温度梯度较小,温度场误差也很小。从总体误差分布看,500 hPa温度场可以较好地反映整个对流层非系统误差分布特征。在高纬度地区中低层出现非系统误差大值区可能是由于初始场误差在误差来源中占比较高,极地地区的大值可能与GRAPES_GFS 2.0自身的缺陷有关。相较于位势高度场,温度场的非系统误差大值范围随预报时效的增加变化明显,增速也高于线性增速。
200 hPa和850 hPa分别对应高低空急流,是风场预报中的关注重点。由图 6可知,200 hPa纬向风场的非系统风速误差基本沿纬向分布。在预报时效为1 d时,误差大值位于赤道附近。随着预报时效增加,误差大值逐渐向南、北半球的中纬度地区,特别是海洋地区转移,这与NCEP FNL分析资料的风速大值分布基本一致。图 7所示850 hPa风场NCEP FNL分析资料对应的纬向风平均场在北太平洋、北大西洋、南大洋地区存在闭合高值中心,南半球的纬向风场较为平直。与此对应的是,北半球纬向风风速高值中心区域和南半球的中纬度地区误差较大。而且随预报时效增加,整个预报时段内这些区域的非系统误差增速均高于线性增速。
由图 8可知,纬向平均风场的非系统误差分布以60°N和60°S的300 hPa附近为中心向四周递减,大值区域大致分布在40°~80°N和40°~80°S的200~500 hPa,误差大值与NCEP FNL分析资料对应的纬向风平均场风速大值区相吻合,呈双中心结构,且具有很好的南、北半球对称性。北半球误差中心位于急流轴北侧,南半球误差中心则位于急流轴南侧,从急流轴到误差核心区的气旋性切变有可能对误差的变化产生影响。在预报时效为1 d时,赤道地区在对流层顶附近有1个小的误差中心区,随着预报时效的增加逐渐消失。该现象说明赤道地区纬向风场在对流层顶附近的初始误差较大而增速较缓慢,这也与200 hPa纬向风场的误差演变情况类似。由此可以大致推断,低纬度地区的误差增速在整个对流层小于中高纬度地区。
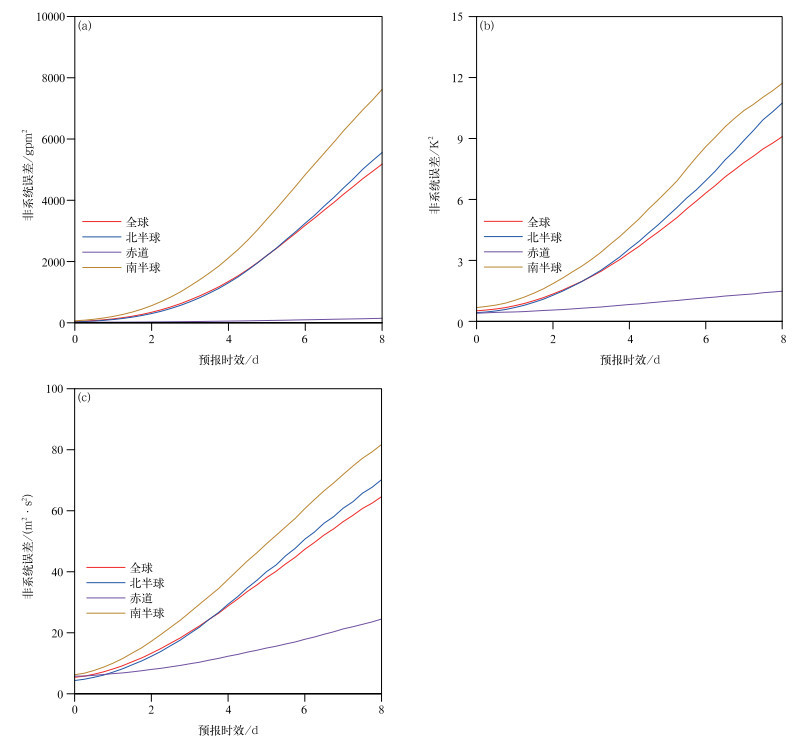
由以上分析可以看到,GRAPES_GFS 2.0模式的非系统误差空间分布不均匀,为了更加清晰地展现各空间区域的误差随预报时效的增长情况,绘制了500 hPa位势高度场、温度场、纬向风场的平均非系统误差图(图 9)。全球和南、北半球的位势高度场误差随时间增长的曲线走势基本相似,先呈指数函数增长、后呈线性增长的态势,误差数值也大体一致。赤道地区的误差相对较小,与其他3条曲线有一个数量级的差距,且预报误差一直呈线性增长,增幅较小。总体来说,位势高度场全球非系统误差随时间的演变趋势主要由南、北半球的中高纬度地区主导。与位势高度场类似,温度场的误差从大到小排序也是南半球、北半球、全球、赤道地区,但4条曲线大体呈线性增长,并在第8天有达到饱和态的趋势。这可能是由于温度场初始误差的非线性增长较弱,模式缺陷所造成的内部误差占比较高所致。纬向风场的曲线走势与温度场类似,但误差数值明显大于温度场。
|
|
| 图9 所选取试验时间平均的GRAPES_GFS 2.0模式平均500 hPa位势高度场(a)、温度场(b)、纬向风场(c)预报非系统误差随时间演变 Fig.9 Unsystematic error of geopotential height field(a), temperature field(b), zonal wind field(c) at 500 hPa by GRAPES_GFS 2.0 along with lead time based on the average of selected time | |
非系统误差先呈指数函数增长,后呈线性增长,最后趋于可预报上限的随时间演变态势可以由式(2)[8]表示:

|
(2) |
式(2)中,ε为非系统误差,α为内部误差增长率,S为外部误差,ε∞为可预报上限。该式充分考虑了初始场误差和模式本身缺陷对非系统误差的贡献,并设置了可预报上限防止误差的无限制增长。由所选取试验时间不同区域的位势高度场非系统误差参数反演结果(表略)可知,全球、北半球、南半球的内部误差增长率均约为0.5~0.6,随季节变化略有浮动。全球的外部误差和可预报上限在4月和10月较大,1月和7月较小,而南、北半球则在各自的冬季达到最大。同时,在相同季节时南半球在全球误差中的比例略大于北半球。外部误差与可预报上限之比在所选4个月从大到小依次为南半球、全球、北半球,这说明南半球外部误差占比较高,模式相对于实际气候态的漂移比北半球严重。赤道地区的误差变化规律与其他所选区域不同,这与图 9所示的误差增长曲线相吻合。选取200,500,850 hPa位势高度场的参数反演结果可以更加全面地了解位势高度场的参数分布特征(表略)。随着高度的增加,内部误差增长率、外部误差、可预报上限均逐渐增大,这一现象可能是因为对流层上层位势高度误差数值较大导致误差绝对值也相应较大。但值得注意的是,外部误差与可预报上限的比值反而减小,这表明随着高度的增加,位势高度场的水平均一性越来越好,模式缺陷在非系统误差中的占比逐渐减少。
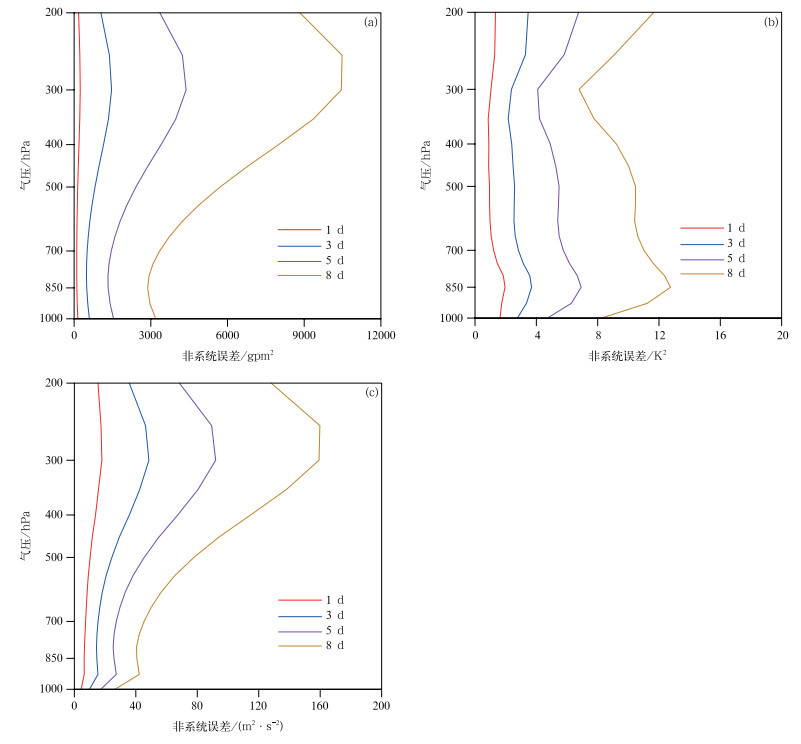
图 10为不同预报时效下误差随高度演变。由图 10a可见,位势高度场误差随高度的变化呈明显的单峰分布,峰值位于300 hPa附近。在300 hPa以下,随预报时效的增加误差持续增长,呈非线性增长态势,且在300 hPa拐点处的误差变化幅度与预报时效成正比。由图 10b可见,温度场的误差走势呈锯齿状,误差大值所在高度位于边界层顶附近区域,低值区在300 hPa附近,在边界层顶至对流层顶误差随高度增加而下降,在300 hPa以上误差随高度增加反而上升。由图 10c可见,不同预报时效下纬向风场误差随高度变化趋势与位势高度场相似,拐点也是在300 hPa附近。非系统误差在300~400 hPa高空急流区急剧增长,随后减小,高度上升到200 hPa附近时,误差值与400 hPa处基本一致。因此,对高空急流区的误差订正是GRAPES_GFS 2.0亟需解决的问题之一。
|
|
| 图10 所选取试验时间平均的GRAPES_GFS 2.0模式的平均位势高度场(a)、温度场(b)、纬向风场(c)在不同预报时效下非系统误差随高度变化 Fig.10 Unsystematic error of geopotential height field(a), temperature field(b), zonal wind field(c) by GRAPES_GFS 2.0 along with height based on the average of selected time | |
3 结论与讨论
非系统误差是模式模拟误差的主要来源之一,主要由初始场误差(外部误差)和模式自身缺陷(内部误差)组成。本文对GRAPES_GFS 2.0位势高度场、温度场和纬向风场的非系统误差的空间分布和时间演变特征进行了详细分析,得到以下主要结论:
1) 非系统误差大值区域主要分布在南、北半球的中高纬度地区,特别是以60°N和60°S为中心的带状区域中。由于南半球下垫面更加均一平坦,等高线相较北半球更为平直且更为密集,因此,南半球条带状分布特征更加明显,误差也基本高于北半球同纬度地区。从季节分布看,南、北半球的非系统误差均在各自冬季达到极盛,且误差呈周期性变化。
2) 在200~1000 hPa各等压面上,不同高度上非系统误差的空间分布态势均大体一致。位势高度场和纬向风场的误差大值均出现在对流层顶附近,温度场误差大值则出现在边界层顶。温度场在对流层中高层随位势高度的增长误差一直下降。随着预报时效的增加,位势高度场的非系统误差先呈指数增长, 后呈线性增长,最终趋于可预报上限,温度场和纬向风场则呈线性增长且增速缓慢。
3) 对位势高度场非系统误差随预报时效增长的曲线进行参数化后发现,在空间区域分布上,南半球的外部误差、可预报上限和外部误差占比均高于北半球,说明GRAPES_GFS 2.0对南半球中纬度地区模拟的模式缺陷较大。随着高度增加,外部误差占比减小,但绝对误差值大于下层,因此,GRA- PES_GFS 2.0在整个对流层均有预报精度提升空间。
通过对GRAPES_GFS 2.0模式模拟的位势高度场、温度场和纬向风场进行误差评估分析,得到误差大值区域和时空分布特征,一方面能够帮助模式研发人员有针对性地增加误差敏感区域地基、探空和卫星遥感观测的资料同化种类和频率。如可以增加误差增长较显著的冬季中高纬度地区卫星资料的使用,并通过加大误差敏感地区观测资料的使用频率,抑制初始误差的非线性增长,从而提高预报准确性。对流层顶和边界层顶附近则需要增加探空和卫星资料进一步提高预报精度。另一方面,GRAPES_GFS 2.0模式对这些误差大值区的模拟也可以采取提高局地模式分辨率、调整物理过程和参数化方案等手段,在不大幅增加运算时长的前提下,尽可能减少误差。因此,对GRAPES_GFS 2.0模式的误差进行详细分析,可以为今后模式的改进提供参考。
致谢: 感谢中国气象局数值预报模式研发中心和业务全体工作人员为本研究提供GRAPES_GFS模拟资料集。
| [1] |
陈德辉, 薛纪善. 数值天气预报业务模式现状与展望. 气象学报, 2004, 62(5): 623-633. |
| [2] |
潘留杰, 张宏芳, 王建鹏. 数值天气预报检验方法研究进展. 地球科学进展, 2014, 29(3): 327-335. |
| [3] |
Lorenz E N. Atmospheric predictability experiments with a large numerical model. Tellus, 1982, 34: 505-513. |
| [4] |
丑纪范, 郑志海, 孙树鹏. 10~30 d延伸期数值天气预报的策略思考——直面混沌. 气象科学, 2010, 30(5): 569-573. DOI:10.3969/j.issn.1009-0827.2010.05.001 |
| [5] |
陈静, 陈德辉. 集合数值预报发展与研究进展. 应用气象学报, 2002, 13(4): 497-507. |
| [6] |
达朝究, 穆帅, 马德山. 基于Lorenz系统的数值天气转折期预报理论探索. 物理学报, 2014, 63(2): 029201. |
| [7] |
于海鹏, 黄建平, 李维京, 等. 数值预报误差订正技术中相似-动力方法的发展. 气象学报, 2014, 72(5): 1012-1022. |
| [8] |
Dalcher A, Kalnay E. Error growth and predictability in operational ECMWF forecasts. Tellus A, 1987, 39: 474-491. DOI:10.3402/tellusa.v39i5.11774 |
| [9] |
邵爱梅, 希爽, 邱崇践. 修正数值天气预报的非系统性误差的变分方法. 中国科学(D辑), 2009, 39(2): 235-244. |
| [10] |
Danforth C M, Kalnay E, Miyoshi T. Estimating and correcting global weather model error. Mon Wea Rev, 2007, 135: 281-299. DOI:10.1175/MWR3289.1 |
| [11] |
Hu S J, Qiu C Y, Zhang L Y, et al. An approach to estimating and extrapolating model error based on inverse problem methods:Towards accurate numerical weather prediction. Chin Phys B, 2014, 23(8): 089201. DOI:10.1088/1674-1056/23/8/089201 |
| [12] |
丑纪范, 任宏利. 数值天气预报——另类途径的必要性和可行性. 应用气象学报, 2006, 17(2): 240-244. |
| [13] |
Yu H P, Huang J P, Chou J F. Improvement of medium-range forecasts using the analog-dynamical method. Mon Wea Rev, 2014, 142(4): 1570-1587. DOI:10.1175/MWR-D-13-00250.1 |
| [14] |
Reynolds C A, Webster P J, Kalnay E. Random error growth in NMC's global forecasts. Mon Wea Rev, 1994, 122: 1281-1305. DOI:10.1175/1520-0493(1994)122<1281:REGING>2.0.CO;2 |
| [15] |
陈德辉, 沈学顺. 新一代数值预报系统GRAPES研究进展. 应用气象学报, 2006, 17(6): 773-777. |
| [16] |
胡江林, 沈学顺, 张红亮, 等. GRAPES模式动力框架的长期积分特征. 应用气象学报, 2007, 18(3): 276-284. |
| [17] |
张萌, 于海鹏, 黄建平, 等. GRAPES_GFS 2.0模式系统误差评估. 应用气象学报, 2018, 29(5): 571-583. |
| [18] |
施晓晖, 徐祥德, 谢立安. NCEP/NCAR再分析风速、表面气温距平在中国区域气候变化研究中的可信度分析. 气象学报, 2006, 64(6): 709-722. DOI:10.3321/j.issn:0577-6619.2006.06.004 |
| [19] |
沈学顺, 苏勇, 胡江林, 等. GRAPES_GFS全球中期预报系统的研发和业务化. 应用气象学报, 2017, 28(1): 1-10. |
| [20] |
Dai Y J, and Coauthors. The common land model. Bull Amer Meteor Soc, 2003, 84(8): 1013-1023. DOI:10.1175/BAMS-84-8-1013 |
| [21] |
Dai Y J, Dickinson R E, Wang Y P. A two-big-leaf model for canopy temperature, photosynthesis, and stomatal conductance. J Climate, 2004, 17(12): 2281-2299. DOI:10.1175/1520-0442(2004)017<2281:ATMFCT>2.0.CO;2 |
| [22] |
Han J, Pan H L. Revision of convection and vertical diffusion schemes in the NCEP global forecast system. Wea Forecasting, 2011, 26(4): 520-533. DOI:10.1175/WAF-D-10-05038.1 |
| [23] |
Lott F, Miller M J. A new subgrid-scale orographic drag parametrization:Its formulation and testing. Q J R Meteorol Soc, 1997, 123(537): 101-127. DOI:10.1002/(ISSN)1477-870X |
| [24] |
McFarlane N A. The effects of orographically excited gravity waves on the general circulation of the lower stratosphere and troposphere. J Atmos Sci, 1987, 44: 1775-1800. DOI:10.1175/1520-0469(1987)044<1775:TEOOEG>2.0.CO;2 |
| [25] |
Palmer T, Shutts G J, Swinbank R. Alleviation of a systematic westerly bias in general circulation and numerical weather prediction models through an orographic gravity wave drag parameterization. Q J R Meteorol Soc, 1986, 112: 1001-1039. DOI:10.1002/(ISSN)1477-870X |
| [26] |
王金成, 陆慧娟, 韩威, 等. GRAPES全球三维变分同化业务系统性能. 应用气象学报, 2017, 28(1): 11-24. |
| [27] |
刘艳, 薛纪善, 张林, 等. GRAPES全球三维变分同化系统的检验与诊断. 应用气象学报, 2016, 27(1): 1-15. |
 2019, 30 (3): 332-344
2019, 30 (3): 332-344



