2. 中国气象局风能太阳能资源中心,北京100081;
3. 中国气象局气象探测中心,北京 100081
2. Wind and Solar Energy Resources Center, CMA, Beijing 100081;
3. Meteorological Observation Center of CMA, Beijing 100081
太阳能作为气候资源的一种,其大规模利用会受到各种气象因素的影响。对于光伏发电,温度是影响其发电效率的重要因素之一。晶体硅太阳电池是光伏发电的主要设备,由于硅材料自身的物理特性,温度上升会引起开路电压和填充因子下降,进而导致输出电功率的下降。根据实验室测定,对于一般晶体硅太阳电池,温度影响系数γ在-0.35%/℃与-0.5%/℃之间,即在标准测试温度以上,温度每升高1℃,太阳电池的发电效率下降0.35%~0.5%[1-3]。
太阳电池发电时其温度会随着外界气象条件,尤其是气温和太阳辐射的变化而变化。在光伏电站的设计中,通常采用温度折减系数cT来定量描述实际气象条件下温度变化对光伏发电量的影响,该系数可表示为
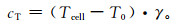
|
(1) |
式 (1) 中,Tcell为电池板温度,T0为标准测试温度 (即25℃)。由于我国气候特征多样,高温区域面积很广[4-8],温度对光伏发电的影响显著,cT成为光伏电站设计中的必要参数之一。
由式 (1) 可知,确定合理的温度折减系数,只需知道Tcell。而我国目前并没有充足的外场实测电池板温度数据,从而为cT的定量化带来很大不确定性。在不同地区光伏电站的设计中,该系数往往依据经验甚至随意设定,取值范围为1%~6%,差别较大,且对气候背景的考虑很不充分。
本文针对该问题,利用北京南郊太阳能试验站实测数据,分析气象要素对太阳能电池板温度的影响,并建立相关关系,尝试得到由气象要素推算电池板温度的方法,从而为温度折减系数的合理设定提供依据。
1 资料与方法 1.1 资料北京南郊太阳能试验站 (以下简称试验站) 位于北京市观象台内 (39.93°N,116.28°E),海拔高度为54.8 m。试验站由中国气象局气象探测中心于2009年7月建成,主要为分析研究光伏发电与气象要素的关系提供第一手实测数据,测量项目包括常规气象要素、多种斜面上的太阳辐射和光伏电池发电功率以及电池板温度等。
本文所用数据分为两类:试验站2010年逐时实测数据,包括以纬度角倾斜放置的单晶硅电池板温度 (以下简称板温,记为Tcell) 和以纬度角倾斜放置的总辐射表测量数据 (以下简称斜面辐照度,记为IGS);与试验站相邻的北京市观象站 (区站号为54511) 同期数据,包括1.5 m高度的气温 (百叶箱温度,记为Tair)、下垫面温度 (0 cm地表温度,简称地表温度,记为Tground) 和水平放置的总辐射表测量数据 (简称水平面辐照度,记为IGH),来源于国家气象信息中心。
试验站由于仪器故障、维修以及增添设备等原因,于2010年8月5—11日、8月29—30日、9月13—27日缺测,数据完整率约94%,满足研究需要。
1.2 数据处理方法考虑到太阳能电池仅在白天发电,而温度对其效率的影响也只在发电时才有体现,因此研究中挑选白天数据进行分析。根据《地面气象观测规范》中的方法和附表[9],确定试验站每日的日出和日落时间,由此挑选出白天数据,共4222个样本进行分析,约占全年有效数据的51%。文中所用的温度日平均值是对每日白天的数据求平均得到。
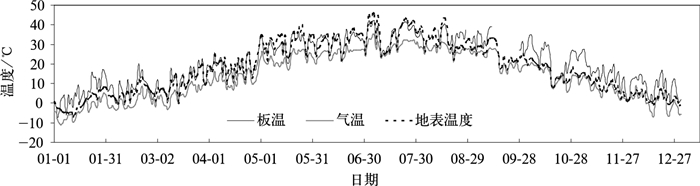
2 时间变化 2.1 年变化图 1给出了2010年板温、气温和地表温度白天日平均值随时间的变化曲线,白天逐时值在4个季节和全年的统计结果列于表 1。由图 1和表 1可知,3种温度年变化趋势基本一致,近似呈正态分布;春、夏季 (3—8月) 板温和地表温度数值相近 (平均值相差不到1℃),均明显高于气温 (高6℃以上);秋、冬季 (9—12月、1—2月) 地表温度和气温比较接近 (平均值相差约2℃),而板温则明显高于两者 (高6℃以上);从全年看,3条曲线最高值是地表温度,为46.2℃(7月5日),最低值是气温,为-11.1℃(1月5日),而板温则是年平均值最高。
|
|
| 图 1. 试验站2010年板温、气温和地表温度白天日平均值随时间变化曲线 Fig 1. Variation of daytime average solar cell temperature, air temperature and ground temperature in 2010 at experiment station | |
|
|
表 1 试验站2010年白天板温、气温和地表温度统计结果 (单位:℃) Table 1 Statistics of daytime solar cell temperature, air temperature and ground temperature in 2010 at experiment station (unit:℃) |
3种温度的年变化与北京地区不同季节的气候特点密切相关,如春季多大风、夏季多降雨、秋季凉爽、冬季干冷等,但由于温度变化的复杂性,气温主要受气象因素 (辐照、风速、湿度、空气质量等) 影响,地表温度受气象要素和地表覆盖共同影响,而板温除了与气象要素有关外,还受其自身工作状态下发热的影响,因此难于应用某一种或几种因素同时解释上述变化特点,有关这方面的机理研究将通过对多种气象要素逐时数据的细致分析进一步开展。
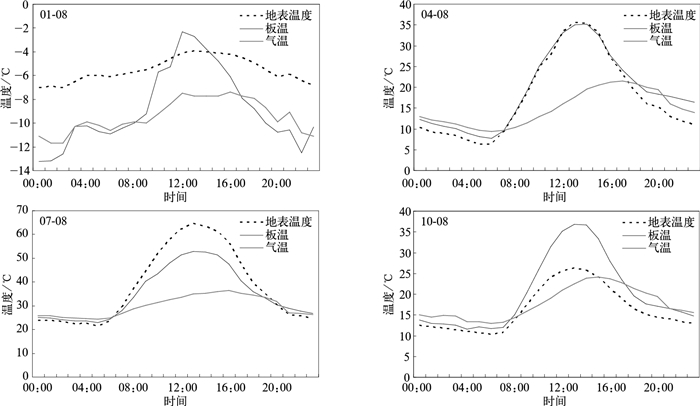
2.2 日变化图 2是从2010年4个季节中分别挑选一日 (1月8日、4月8日、7月8日、10月8日) 得到的板温、气温和地表温度的日变化曲线,相应的天气状况如表 2所示。
|
|
| 图 2. 试验站2010年典型日板温、气温和地表温度的日变化曲线 Fig 2. Diurnal variation of solar cell temperature, air temperature and ground temperature of typical days in 2010 at experiment station | |
|
|
表 2 试验站2010年典型日的天气状况 Table 2 Weather conditions of typical daytime in 2010 at experiment station |
1月8日,阴天,有雾霾,14:00(北京时,下同) 的能见度仅12 km。气温和地表温度变化趋势基本一致,均较为平缓,而单晶硅电池的板温则波动较大。从具体数值看,全天气温在-11.7~-7.4℃之间变化,地表温度比气温平均高5℃左右;全天板温在-13.3~-2.3℃之间变化,呈现出迅速升高、又迅速下降的特征,中午的板温高于地表温度,上午和下午的板温介于地表温度和气温之间,夜间的板温则低于气温,这一方面与冬季的气候特点有关[10],另一方面也受当天天气状况的影响。
4月8日,多云天气,全天的平均总云量达到90%,风速较大,能见度较好。板温与地表温度的大小和变化趋势均几乎完全一致,气温则完全不同。夜间气温最高,板温次之,地表温度最低,06:00以后板温和地表温度迅速升高,并于中午达到峰值,而后又迅速下降,且地表温度比板温下降更快,气温在早上06:00以后缓慢升高,直到下午才达到峰值,此后的下降也相对较缓。从具体数值来看,全天气温在9.4~21.5℃之间变化,最高值出现在17:00,全天地表温度在6.3~35.6℃之间变化,最高值出现在13:00,全天板温在7.8~35.2℃之间变化,最高值出现在14:00,三者的最低值均出现在06:00。
7月8日,晴间多云,能见度达到30 km。三者变化趋势之间的关系与4月8日相似,但地表温度要明显高于板温。从具体数值来看,全天气温在24.3~36.4℃之间变化,最高值出现在16:00,全天地表温度在21.5~64.6℃之间变化,最高值出现在13:00,全天板温在23.0~53.0℃之间变化,最高值出现在13:00,三者的最低温度均出现在05:00。
10月8日,晴间多云,有雾霾,能见度仅8 km。三者变化趋势之间的关系与4月8日相似,但板温要明显高于地表温度,气温和地表温度大小相当。从具体数值来看,全天气温在13.0~24.2℃之间变化,最高值出现在15:00,全天地表温度在10.4~26.4℃之间变化,最高值出现在13:00,全天板温在11.6~36.8℃之间变化,最高值出现在13:00,三者的最低温度均出现在06:00。
综合以上分析,虽然在不同的季节和天气条件下,板温的变化有其自身特点,但从全年来看,它与气温和地表温度在变化趋势上存在一致性,这使得由气象要素推算板温成为可能。
3 相关分析根据Ross等[11]的试验研究,板温不仅与气温相关,还与太阳电池的性能和辐照度有关:
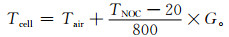
|
(2) |
式 (2) 中,TNOC是光伏电池额定工作温度,指在辐照度为800 W·m-2、气温为20℃、风速为1 m·s-1的外部环境条件下光伏电池的温度;性能最佳的组件为33℃,性能最差的组件为58℃,典型组件为48℃;G是太阳电池板上的辐照度,单位为W·m-2;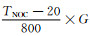
式 (2) 是在特定试验条件下测定的板温与气象要素的关系,在现实条件下,气温数据比较容易从气象站获得,而太阳电池板上的辐照度数据却不易从现有的数据中获取,需要特定的测量。因此,实际气象条件下的温度折减系数仍然难以确定。为此,参照式 (2) 思路分析了板温与气温和斜面辐照度的综合相关,给出了板温与气温和水平面辐照度的综合相关关系、板温与地表温度的相关关系、板温与气温的相关关系等,以便根据不同的数据储备推算合理的板温和温度折减系数。
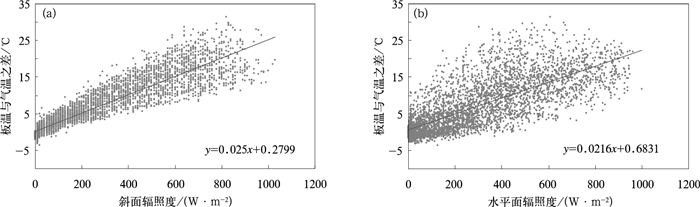
3.1 板温与气温和辐照度综合相关分析图 3a是2010年全年白天逐时的板温与气温之差和斜面辐照度的相关关系,两者相关系数达0.92。由图 3a可以看出,当辐照度较低时,数据点比较集中,而当辐照度较高时,则相对离散,这说明板温的变化可能还会受到其他气象要素,如风速、湿度、降水等的影响。将图 3a中的趋势线方程转换成类似式 (2) 的关系,得
|
|
| 图 3. 板温与气温之差和辐照度的相关关系 (a) 斜面辐照度, (b) 水平面辐照度 Fig 3. Correlation of the difference between solar cell temperature and air temperature to solar irradiance (a) slope solar irradiance, (b) horizontal solar irradiance | |
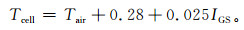
|
(3) |
气象站的辐射观测并没有斜面辐照度,只有水平面辐照度,图 3b给出了板温与气温之差和水平面辐照度的相关关系,两者相关系数仅为0.75。由图 3b可以看出,数据点比较离散,说明水平面辐照度与斜面辐照度随时间的变化趋势并不完全一致。将图 3b中的趋势线方程转换成类似式 (2) 的关系,得
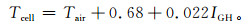
|
(4) |
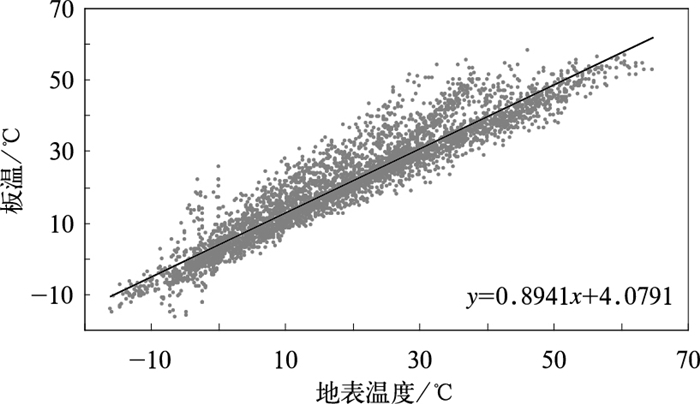
由于我国目前仅有98个气象站开展辐射观测,辐照度的数据并不充足,因此,根据前面时间变化分析,图 4给出了板温与地表温度之间的相关关系, 两者的相关系数达到0.94。由图 4可以看出,板温与地表温度的相关系数甚至超过了板温与气温和斜面辐照度的综合相关,数据点的离散程度也明显较低,由于两种温度的变化原理类似,地表温度的变化不仅与气温和辐射有关,还可能受风速、湿度和降水等气象要素的影响。将图 4中的趋势线方程转换成板温的推算方程,得
|
|
| 图 4. 板温与地表温度的相关关系 Fig 4. Correlation between solar cell temperature and ground temperature | |
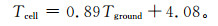
|
(5) |
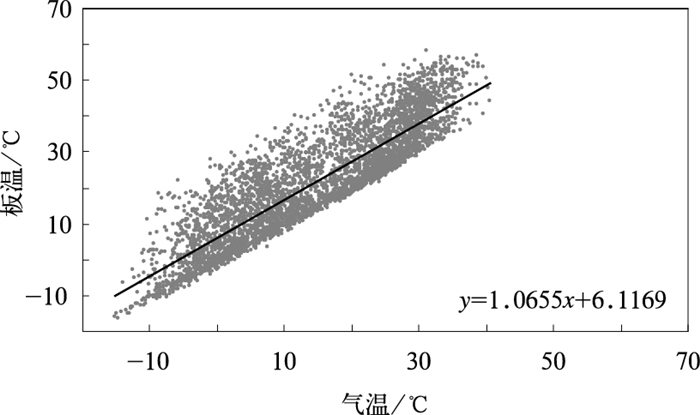
虽然地表温度是气象站的基本观测要素之一,但其观测方法和要求相对复杂,观测数据的质量也有待提高[12-15],图 5给出了板温与气温之间的相关关系,两者之间的相关系数为0.88,由图 5可以看出,数据点的下边缘比较平齐,可视为气温转换板温时的边界条件。将图 5中的趋势线方程转换成板温的推算方程,得
|
|
| 图 5. 板温与气温的相关关系 Fig 5. Correlation between solar cell temperature and air temperature | |
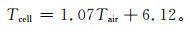
|
(6) |
为检验上述相关方程的计算效果,将各相关关系用于推算2009年8—10月的板温,并与同期的实测板温进行对比 (表 3)。由表 3可以看出,式 (3),即由气温和斜面辐照度推算的板温与实测值最接近,3个月的综合相关系数超过0.97;式 (4),即由气温和水平辐照度推算的板温与实测值也很接近,3个月的相关系数明显高于该式自身的相关系数,这主要是由于在这3个月期间,斜面辐照度和水平辐照度比较接近 (两者的差异主要体现在冬季);式 (5),即由地表温度推算的板温与实测值的相关系数也超过0.95;式 (6),即由气温推算的板温与实测值相差最大,相关系数为0.86。
|
|
表 3 2009年8—10月的板温实测值与推算值及其相关系数 Table 3 Comparison of calculated Tcell with observed Tcell in Aug, Sep and Oct of 2009 with their correlation coefficients |
综合以上分析,板温与气温和斜面辐照度的综合相关以及与地表温度的线性相关最好,也更符合温度变化的内在联系,在数据充足且质量有保证的情况下,是推算板温和温度折减系数的最佳选择;板温与气温的线性相关较好,但由于两者的影响因素不完全相同,内在联系不密切,只可作为仅有气温实测数据时的替代选择;板温与气温和水平辐照度的综合相关最差,但可用于极端板温推算。
3.4 高温条件下的相关分析在以上相关分析中,板温与气象要素之间均存在一定程度的离散,所建立的板温推算方程主要反映趋势线附近的状况,通过将高值拉低和低值拔高使所得结果的平均值与实测值比较接近 (如表 3所示),但却因此而不能反映极端高温或低温的情形。如利用式 (6) 进行气温到板温的转换,得到试验站2010年的最高板温为49.4℃,比实测值低近9℃,极端高温的情形被掩盖了。
为了能够在没有斜面辐照度或地表温度的情况下,仍可根据气温推算高温情形下的板温,这里挑选白天气温35℃以上的数据 (共67个样本) 进行分析 (图 6)。由图 6可以看出,气温高于35℃,板温与气温之差和水平辐照度的综合相关性明显变好,相关系数提高到0.87,数据点的离散程度也比图 3b明显降低。将图 6中的趋势方程转换成极端板温的推算方程,得
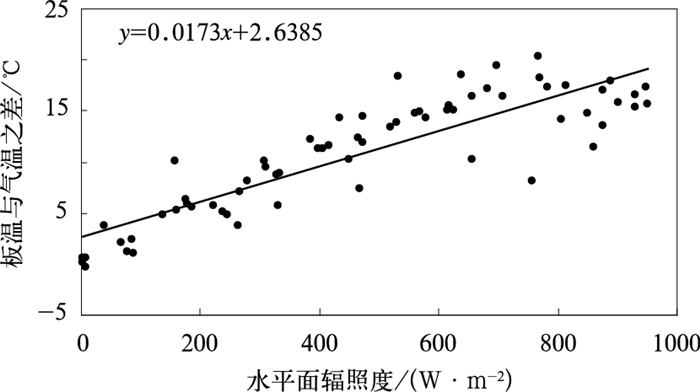
|
|
| 图 6. 气温高于35℃时,板温与气温之差和水平辐照度的相关关系 Fig 6. Correlation of the difference between solar cell temperature and air temperature to horizontal solar irradiance, when air temperature higher than 35℃ | |
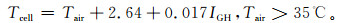
|
(7) |
根据式 (7) 计算试验站最高板温为57.2℃,与实测值接近。
需要特别指出的是,以上均是基于1年逐时实测数据所建立的相关方程,因此在用于推算板温时,输入数据也应是逐时的气温、辐照度或地表温度。
4 北京地区的温度折减系数利用试验站全年逐时板温数据,在式 (1) 的基础上,采用加权计算的方法,近似确定年平均的光伏发电温度折减系数cT,其中假定板温在25℃以下时,晶体硅电池的效率为100%。
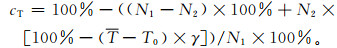
|
(8) |
式 (8) 中,N1为一年中白天的总时次,N2为白天板温大于25℃的时次,T为N2条件下的平均板温,T0为太阳能电池板实验室标准测试温度 (即25℃),γ为太阳能电池板的温度系数,本文对晶体硅电池取0.4%/℃。式 (8) 中所用温度均为板温,若无实测数据,则需根据式 (3)~式 (7) 由气象要素推算。
表 4是2010年试验站白天逐时板温实测数据的统计结果,据此利用式 (8) 计算得到年平均温度折减系数为1.82%,最高温度折减系数达到13.3%。
|
|
表 4 试验站2010年白天逐时实测板温统计 Table 4 Statistic of hourly real-time solar cell temperature at daytime in 2010 of experiment station |
由于气温是变化的,以上计算结果的气候代表性如何,还需具体分析。图 7给出了北京市观象台近30年的气温距平变化。由图 7可以看出,北京地区近30年平均气温显著升高,但2010年的平均气温 (12.6℃) 比30年平均值 (12.9℃) 偏低0.3℃,因此,上述温度折减系数可能略低于多年平均值。同时,考虑到试验站数据缺测时段分布在温度较高的8月、9月,也可能使温度折减系数偏低。综合考虑,北京地区的光伏发电温度折减系数可近似取2%。
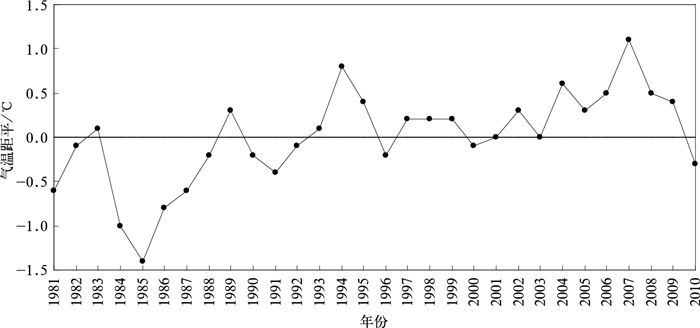
|
|
| 图 7. 1981—2010年北京市观象台近30年年平均气温距平变化 Fig 7. Variation of air temperature anomaly at Beijing Weather Observatory during 1981—2010 | |
5 结论与讨论
利用北京南郊太阳能试验站2010年实测数据,分析了板温随时间的变化及其与各气象要素的关系,主要结论如下:
1) 板温的年变化趋势与气温和地表温度基本一致,但数值大小在不同季节有变化,春、夏季 (3—8月) 板温和地表温度数值相近,均明显高于气温,秋、冬季 (9—12月、1—2月) 地表温度和气温比较接近,而板温则明显高于两者。
2) 从相关关系来看,板温与气温和斜面辐照度的综合相关以及板温与地表温度的线性相关系数都在0.90以上,也更符合温度变化的内在联系,是推算板温和温度折减系数的最佳选择;板温与气温的线性相关系数为0.88,可作为仅有气温实测数据时的替代选择;板温与气温和水平辐照度的综合相关系数仅有0.75,但当气温为35℃以上时,相关系数提高到0.87,该关系可用于推算极端板温和相应的温度折减系数。
3) 根据2010年实测的板温数据,综合考虑气候变化和数据缺测因素,得到北京地区年平均的光伏发电温度折减系数约为2%,极端最高达到13.3%。
文中给出了板温与气象要素的多种相关方程,从温度变化的内在联系看,板温与气温和斜面辐照度的综合相关或与地表温度的线性相关是最佳选择,但斜面辐照度一般没有逐时实测数据,而地表温度实测数据可能存在质量问题;从现实可行性考虑,气温是气象站最基本的观测要素,容易获得且数据质量有保证,水平辐照度在有辐射观测的台站也可获得,因此板温与气温的线性相关方程可能是最实用的,而板温与气温和水平辐照度的综合相关则可以作为辅助方程,用于推算气温较高情况下的板温。
由于北京南郊太阳能试验站的实测数据有缺测情况,且主要分布在8月、9月气温较高的时段,对上述相关方程会有一定影响。另外,从相关方程的稳定性来看,1年的数据仍显不足,这些问题的解决都需要更长时间、更多地点实测数据的积累和分析。
| [1] | 杨金焕. 太阳能光伏发电应用技术. 北京: 电子工业出版社, 2009. |
| [2] | Wenham S R, Green M A, Watt M E, 等. 应用光伏学. 狄大卫, 高兆利, 韩见殊, 等译. 上海: 上海交通大学出版社, 2008. |
| [3] | Roger A M, Jerry V. 光伏系统工程: 第3版. 王一波, 廖华, 伍春生, 译. 北京: 机械工业出版社, 2012. |
| [4] | 杨萍, 刘伟东, 王启光, 等. 近40年我国极端温度变化趋势和季节特征. 应用气象学报, 2010, 21, (1): 29–36. DOI:10.11898/1001-7313.20100104 |
| [5] | 于淑秋. 近50年我国日平均温度的气候变化. 应用气象学报, 2005, 16, (6): 787–793. DOI:10.11898/1001-7313.20050603 |
| [6] | 周国华, 王盘兴, 罗小莉, 等. 基于160站资料的我国表面气温异常特征. 应用气象学报, 2011, 22, (3): 283–291. DOI:10.11898/1001-7313.20110304 |
| [7] | 周云, 钱忠华, 何文平, 等. 我国夏季高温极值的概率分布特征及其演变. 应用气象学报, 2011, 22, (2): 145–151. DOI:10.11898/1001-7313.20110203 |
| [8] | 董立新, 杨虎, 张鹏, 等. FY-3A陆表温度反演及高温天气过程动态监测. 应用气象学报, 2012, 23, (2): 214–222. DOI:10.11898/1001-7313.20120210 |
| [9] | 中国气象局. 地面气象观测规范. 北京: 气象出版社, 2003. |
| [10] | 李维京, 李怡, 陈丽娟, 等. 我国冬季气温与影响因子关系的年代际变化. 应用气象学报, 2013, 24, (4): 385–396. DOI:10.11898/1001-7313.20130401 |
| [11] | Ross R G Jnr, Smokler M I.Flat-Plate Solar Array Project-Final Report, Vol.Ⅵ: Engineering Sciences and Reliability.JPL Pub No.86-31, 1986. |
| [12] | 李耀宁, 李艳, 李珊珊. 地温观测常见问题及报表数据处理方法. 气象科技, 2011, (3): 348–351. |
| [13] | 张慧智, 史学正, 于东升, 等. 中国土壤温度的空间插值方法比较. 地理研究, 2008, 27, (6): 1299–1307. |
| [14] | 邵全琴, 孙朝阳, 刘纪远, 等. 中国城市扩展对气温观测的影响及其高估程度. 地理学报, 2009, 64, (11): 1292–1302. DOI:10.3321/j.issn:0375-5444.2009.11.002 |
| [15] | 马柱国, 符淙斌, 任小波, 等. 中国北方年极端温度的变化趋势与区域增暖的联系. 地理学报, 2003, 58, (增刊): 11–20. |
 2014, 25 (2): 150-157
2014, 25 (2): 150-157



