气温要素表征气候的热量指标[1], 也是气候变化研究的最基本要素。文献[2]指出, “在过去的130年中全球平均的地面年平均气温有0.6 ℃的增温趋势”。我国许多气候研究人员也以气温为指标, 得出了气候变暖的结论[3~7]。
对于气温要素的平均值, 我国气候研究人员大部分使用的是近50年的观测资料。导致长期资料序列非均一的因子有观测台站位置迁移、观测时次变化、平均方法改变、仪器变化、台站邻近环境变化等[8]。我国在1961年后在观测规范中对气温要素的观测从观测时制、观测时次、统计方法上均有改变。观测时制从1960年前的地方平均太阳时改为全国统一的北京时 (即120°E的地方平均太阳时); 4次的观测时次由01 :00、07 :00、13 :00、19 :00改为02 :00、08 :00、14 :00、20 :00;3次观测统计日平均气温的方法也由3次加权法 (即07 :00、07 :00、13 :00、19 :00的平均) 改为目前规范规定使用的方法。目前我国699个基本 (准) 站中有36个站原为3次观测的气候站 (占基本站的5%), 同时我国2435个气象台站中, 约有1736个气候站是3次观测。因此目前在我国使用的近50年平均气温的资料中, 大约有71%的站是利用3次观测实测值和替代值统计的平均, 只有29%的站是4次实测值平均。气温的4次观测的算术平均值, 是均匀地选取了一日中的4个时次, 基本代表了台站气温的日变化, 因此, 4次观测的算术平均值可以认为是反映了台站的真实气温状况。但是, 由3次观测实测值和替代值计算得出的日平均气温值, 与4次观测的平均值是否存在差异, 差异有多大, 差异是否有变化, 其差异值是否会影响到使用平均气温要素对气候的分析, 譬如对城市热岛的分析等等问题, 国外气候研究人员很重视, 如Karl等对资料的观测时间影响进行了研究, 并做了订正[9]。
本文试图利用我国最全面的基本 (准) 站资料, 探讨由不同计算方法计算的气温平均值的差异, 为研究人员在使用平均气温进行气候分析时提供帮助。
1 资料及计算方法为了显露不同方法计算气温平均值的差异, 采用“地面气象观测规范”[10]规定的计算方法, 即目前我国计算气温平均值的方法。1961年后气温序列的观测时制、观测时次是统一的。为了只揭示1961年后气温平均值统计方法的差异, 本文选取了我国699个基本 (准) 站自1961年到2002年的4次观测资料及逐日最低气温观测资料, 即采用4次观测值计算平均和同一个站同日3次观测值计算平均的方法, 以期比较其差异。资料均经过了国家气象中心气象资料室的质量检验。
统计的项目有:利用各站4次观测记录, 用4次算术平均方法计算每日平均气温值; 根据“地面气象观测规范”规定, 3次观测站当配备有温度计时, 用20 :00和08 :00的自记值内插值代替02 :00观测值; 在未配备自记温度计时, 利用各站逐日最低气温及3次 (08 :00、14 :00、20 :00) 观测记录计算每日平均气温。其中02 :00气温用当日最低气温与前一天20 :00气温之和的算术平均值代替, 再利用02 :00、08 :00、14 :00、20 :00的算术平均方法求得该日平均气温。计算各站逐日4次平均值与3次加权平均值的差值 (简称4次与3次差值); 计算各站历年各月及年的4次与3次差值的平均值及累年4次与3次差值的平均月、年值; 计算各站累年4次与3次差值平均月值的最大值及出现的月份; 计算4次与3次差值年平均值的线性趋势, 并进行了相关系数的显著性检验。
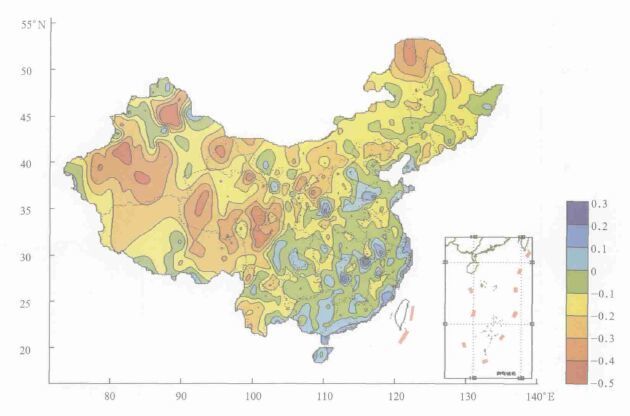
2 结果分析 2.1 4次与3次差值年平均的空间分布特征4次与3次差值年平均图 (彩图1) 反映了明显的空间分布特征。由图可见, 我国平均气温4次与3次差值的年平均存在明显的东南地区与西部、北部地区差异。
|
|
| 图 1. 我国平均气温4次与3次差值的年平均分布图 (单位:℃) | |
(1) 在东南部地区 (110°E以东、40°N以南的区域内), 4次与3次差值的年平均值除局部地区外, 数值大于-0.1 ℃, 是正偏差 (即差值大于0.0) 分布的主要地区。在广东, 广西, 湖南、湖北、江西的连接处, 东部沿海地区, 其正偏差达到0.2 ℃以上。
(2) 在我国西部、北部地区, 100°E以西、40°N以北区域内, 4次与3次差值的年平均基本呈负偏差, 而且经度愈西其负偏差愈大。在青藏高原西部、新疆西北部最大年差值达-0.4 ℃以上。在东北地区, 也基本呈负偏差。在东北的最北部, 存在一个最大负偏差的地区。
我们更关注的是年差值大的台站, 从4次与3次差值的年平均值大的台站分布更清楚地反映其空间分布特征。
4次与3次差值年平均绝对值在0.3 ℃的站点分布图 (图2) 也可以明显看出, 共有66个站4次与3次差值年平均绝对值达0.3 ℃, 其中西部和最北部有64个站年平均差值为-0.3 ℃(用
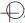
|
|
| 图 2. 我国平均气温4次与3次差值年平均绝对值为0.3 ℃的站点分布图 | |
4次与3次差值的年平均绝对值在0.4 ℃的站点分布图 (图略) 表明, 4次与3次差值的年平均在-0.4 ℃的站点共30个站, 除我国最北部有两个站外, 其余全部分布在110°E以西地区。
4次与3次差值的年平均绝对值在0.5 ℃的站点为51633(新疆拜城41°47′N, 81°54′E)、52645(青海野牛沟38°25′N, 99°35′E)、56043(青海果洛34°28′N, 100°15′E)、56152(四川色达32°17′N, 100°20′E)4个站, 是年平均绝对值最大值的站, 全部在101°E以西的地区。
从总的情况看, 共有100个台站, 其4次与3次差值的年平均绝对值大于等于0.3 ℃, 占总台站数的14.3%, 而其中98%的站分布在西部地区。这个较大的数值和不小的比例, 应该引起我们的关注。
2.2 4次与3次差值月平均最大值的空间分布特征从4次与3次差值月平均的最大值图 (图略) 也可以明显看出, 存在着显著的东南部与西部、北部差异, 其分布状况与年平均分布类似。
在西部地区, 4次与3次差值的月平均最大值为负偏差, 而且偏差幅度比年偏差更大。在青藏高原西部, 偏差达到-0.6~-0.8 ℃以上, 新疆北部达到-0.8 ℃以上。在我国东北的最北部, 差值达到-0.8 ℃以上, 负偏差相当大。而在东南部地区基本为正偏差, 尤其是东南部沿海地区, 正偏差达0.2~0.4 ℃以上。
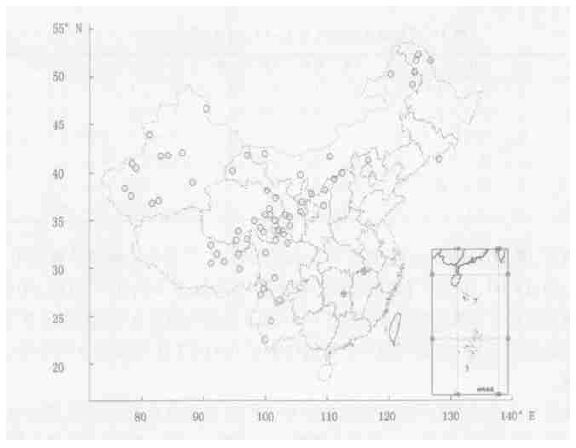
从4次与3次差值月平均的最大值出现月份图 (彩图3) 中可以看出, 我国大部地区4次与3次差值月平均的最大值出现在春、夏季。在东北、西北、西部地区, 最大差值大多出现在春、夏季。在东南、南部地区最大差值大多出现在冬季。
|
|
| 图 3. 我国平均气温4次与3次差值的月平均最大值出现月分布图 | |
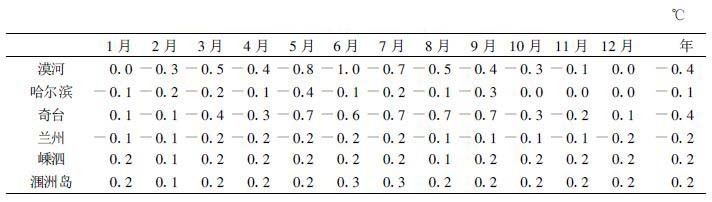
4次与3次月平均差值各地区有着季节变化的差异。表1中各站分别代表东北、西北、西部、东南、南部地区。从中可以看出:4次与3次月平均差值在东北和西北部地区冬季均比较小, 而春、夏季是差值最大的季节, 东南、南部地区季节变化不明显。
|
|
表 1 代表站4次与3次1~12月 (年) 平均差值 |
如前所述, 我国自1961年后, 对于4次观测的台站, 气温平均值的计算采用了4次 (02 :00、08 :00、14 :00、20 :00) 气温观测值的算术平均方法, 对于只有3次 (08 :00、14 :00、20 :00) 观测的台站。如果未配备自记温度计, 采用了观测气温值3次加权的计算方法, 用该日最低气温和前日20 :00的气温的平均值代替02 :00的气温, 再进行4次平均, 即本文模拟的方法。
造成4次与3次差值的因素可能有各地天气系统、地形差异等, 但是从反映出的主要特点, 不同的计算方法是差异产生的主要因素。从计算方法可以看出, 两者的数值差异由两个因子决定, 其一是20 :00的观测气温值, 其二是最低气温观测值。
(1) 20 :00的观测气温值
自1961年后我国气温观测统一使用北京时的时制, 北京时为120°E地方平均太阳时。时制是产生差异的重要原因之一。
在我国西部地区, 由于地方平均太阳时差, 在北京时为20 :00的时刻, 西部地区未到地方平均太阳时20 :00, 最西部地区要相差近3个小时, 当地的地方平均太阳时还未到20 :00, 在气温日变化的情况下, 温度尚未明显下降, 北京时20 :00与最低气温的平均值大于02 :00的气温, 即3次加权平均值加大了20 :00观测气温 (温度值较高) 的权重, 因此要比用4次算术平均计算值偏高。
在我国东北地区, 分析其原因主要是纬度造成的影响。如在东北地区最北部的夏季, 太阳日落时间较南部地区要晚近2个小时。如北纬53°的漠河7月日落时间为地方时20 :30, 而北纬23°的广州7月日落时间为18 :49。在温度日变化的情况下, 20 :00的温度尚未明显下降。北京时20 :00与最低气温的平均值大于02 :00的气温, 即3次加权平均值加大了20 :00观测气温 (温度值较高) 的权重。同时如表1所示, 根据各月4次与3次的差值来看, 东北地区春夏季差值的影响是最大的。如在漠河, 6月份4次与3次的差值为-1.0, 7月份为-0.7, 而1月份为0.0, 2月份为-0.3(由彩图3也可看到, 东北地区最大差值月出现在春季)。因此, 造成我国东北部地区也出现3次观测计算偏高。
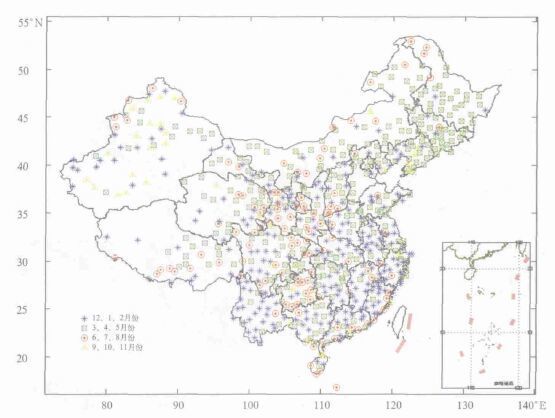
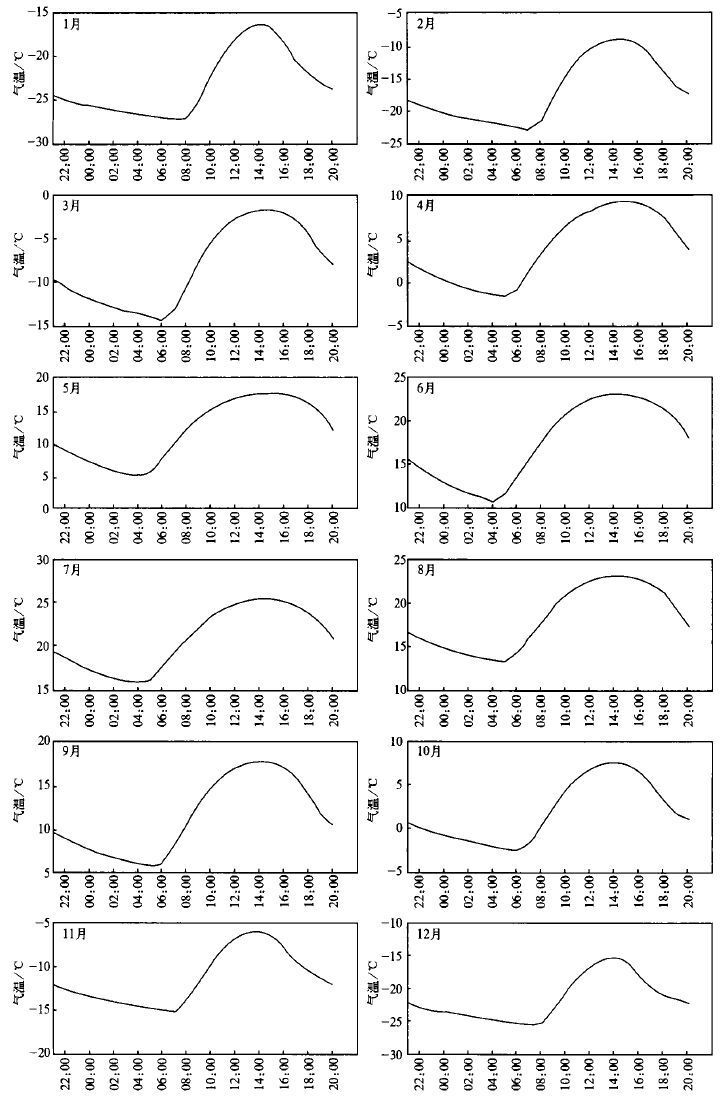
图4、图5分别为位于44°N, 89°E的奇台站 (代表西部地区) 和位于49°N, 127°E的孙吴站 (代表东北地区) 多年平均所得到的各月气温日变化图。图中所标示时间为北京时。从图中可以明显看到, 由于时制的影响, 在西部、北部地区的春、夏季, 20 :00气温和最低点气温的平均值比02 :00气温偏高。而冬季, 20 :00气温和最低点气温的平均值与02 :00相差不大。
|
|
| 图 4. 奇台站各月气温日变化图 | |
|
|
| 图 5. 孙吴站各月气温日变化图 | |
同理, 由于经度的关系, 在东南部地区, 地方平均太阳时20 :00实际上已经超过北京时20 :00, 在气温日变化的情况下, 气温已经为下降趋势, 因为北京时20 :00与最低气温的平均值小于02 :00的气温, 即3次加权平均值加大了20 :00观测气温 (温度值较低) 的权重, 因此要比用4次算术平均计算值偏低。
由于各地区是固定不变的, 其引起偏高的数值应该是一个固定的值。
(2) 最低气温观测值
最低气温有随时间变化的趋势特征。如果最低气温升高的趋势大于平均温度升高的趋势, 则用其作为因子计算出的气温平均值就会随时间变化产生更高的值, 4次与3次差值也就会更大。
在东南部地区如果最低气温不如西部的上升趋势明显, 则用3次加权平均计算得出的值小于4次平均计算值, 因此4次与3次差值呈正值。
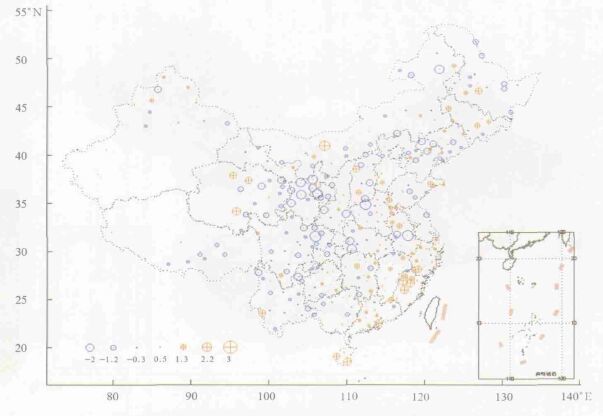
2.3 4次与3次差值历年平均值的趋势分布特征4次与3次差值的年平均具有明显的空间分布特征, 那么这种差值的变化趋势如何呢?为此, 计算了时间长度在25年以上台站4次与3次差值历年平均值的线性倾向趋势。共有466个台站通过了相关系数的显著性检验。由于4次与3次年平均的数值很小, 在计算中将其扩大了1000倍, 以便清晰地显示趋势。从4次与3次差值趋势分布图 (彩图6) 可以看出, 我国绝大部分地区呈负趋势。在我国的中部、西部大部分地区负趋势明显, 尤其是东北的黑龙江、辽宁及山西、甘肃, 青海东部地区, 内蒙古、陕西的大部分也为负趋势。最大负趋势达-2, 也就是-0.002 ℃/a, 相当于50年-0.1 ℃。在江西、福建、广东、海南地区为明显的正趋势, 最大达+3, 也就是+0.003 ℃/a, 相当于50年0.15 ℃。在新疆北部大部分、河南东部地区为正趋势。
|
|
| 图 6. 我国平均气温4次与3次差值的年平均线性趋势分布图 (单位:0.001℃/a) | |
中西部地区负趋势表明, 4次与3次差值的年平均是一个“负值更负”的趋势, 也就是呈现3次计算平均值更高的趋势。产生负趋势是由于最低气温上升所造成的。反映了在这些地区最低气温上升的影响。
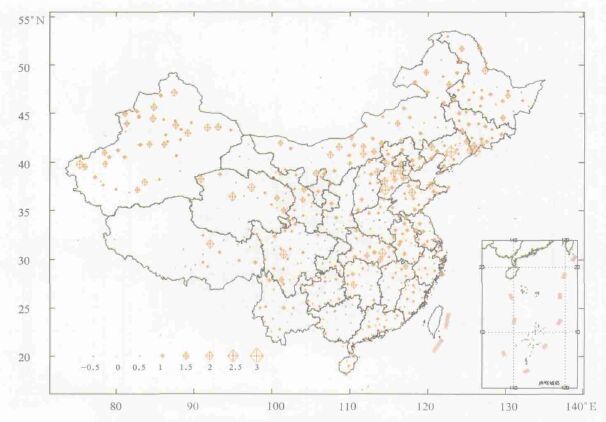
我们制作了我国年平均最低气温线性趋势值分布图 (彩图7)。从图中可以看到, 除极个别台站外, 我国年平均最低气温均呈上升趋势。尤其在黑龙江北部、吉林、辽宁、河北、内蒙古中部、新疆北部地区, 个别地区达到0.15 ℃/a以上。
|
|
| 图 7. 我国年平均最低气温线性趋势分布图 (单位:0.1℃/a) | |
在我国东北、西北、北部最低气温上升已经为许多气候研究人员所证实[11~12]。这一结论与图中的分布是一致的。由于最低气温升高的趋势大于平均温度升高的趋势, 则用其作为因子计算出的气温平均值就会随时间变化产生更高的值, 因此造成了计算出的4次与3次差值在中西部地区负趋势明显。
在江西、福建、广东、海南地区4次与3次差值为明显的正趋势, 也可以看到这一地区年平均最低气温虽然上升, 但相比其他地区, 幅度要小得多。最低气温升高的趋势小于平均温度升高的趋势, 因此, 其4次与3次差值为正值。在新疆北部地区年平均最低气温上升明显, 但最低气温升高的趋势仍然小于平均温度升高的趋势, 因此4次与3次差值为正值。
3 不同方法计算的气温平均值的差异对使用的影响由上文分析中可以看出, 平均气温数据由于计算方法的不同, 差异还是相当明显的。因此, 在使用平均气温资料中应该注意不同观测次数计算气温平均值的差异影响。
(1) 由于台站观测次数不同, 计算气温平均值的计算方法的差异, 会对平均气温的计算值产生影响。这一差异在气候分析中是应该引起重视的。因为在气候变化研究中, 如果某时段使用的气温资料是采用3次加权计算的平均值, 在西部地区, 其数据是偏高的; 在东部地区, 其数值偏低。如果不进行一定的序列订正, 则会产生一定的误差。因此应根据研究的目的, 对使用的平均气温精度要求的不同, 注意序列是否需要做一定的订正, 尤其对原气候站改变为基本 (准) 站的气温资料 (占基本站资料的5%) 的使用时, 更需关注。
在城市热岛效应的研究中, 往往采用城市中心站与郊区站的平均气温差值作为热岛强度指标[13~15], 我国一般城市中心站多为4次观测, 其气温平均值为4次观测的平均, 郊区站多为一般气候站, 其气温平均值多为3次的加权平均值。在西部地区, 如果不加订正的混合使用, 由于3次平均值偏高, 则城市中心站与郊区站的平均气温差值则偏小; 而在东部地区, 由于3次平均值偏低, 则城市中心站与郊区站的平均气温差值则偏大, 会影响城市热岛强度的评估数值。因此, 要特别注意郊区站在计算日平均气温时的计算方法。如果是用3次加权平均值, 而且各站各月差值不同, 在分析热岛强度指标时要注意订正。
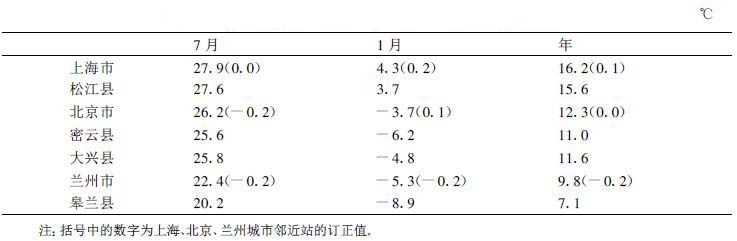
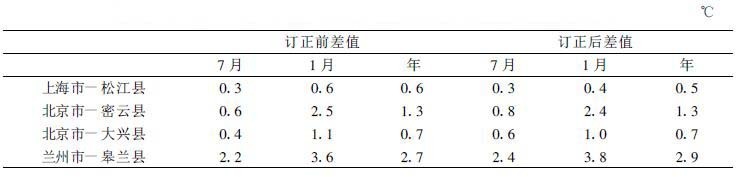
表2列出了上海、北京、兰州3市与周围郊区站 (兰州为邻近站)1971~2000年累年7月、1月及年平均气温值及其邻近站的订正值; 表3为上海等城市与邻近站7月、1月、年平均气温订正前后的差值, 从中看出订正值的影响, 差值反映了热岛强度指标。在上海站1月其热岛强度的评估值从0.6 ℃订正到0.4 ℃, 年热岛强度指标由0.6 ℃订正到0.5 ℃, 分别为原评估值的67%和83%, 热岛强度比原评估值减小比较多, 去除了3次观测站误差的影响, 反映了真实的热岛强度; 北京与密云、北京与大兴的情况也如此。7月份北京与密云的热岛强度原评估值为0.6 ℃, 经订正后为0.8 ℃, 热岛强度比原评估值大, 为原评估值的133%, 增大比较多, 年的热岛强度订正前后无变化; 北京与大兴的情况也相似。兰州市热岛强度经订正后7月、1月、年均比原评估值大0.2 ℃, 分别为2.4 ℃、3.8 ℃、2.9 ℃, 为原评估值的109%、106%、107%。
|
|
表 2 上海等城市7月、1月、年平均气温观测统计值 |
|
|
表 3 上海等城市与邻近站7月、1月、年平均气温订正前后的差值 |
(2) 在气温资料混合使用时, 要了解气温不同计算方法导致的差异, 并分析混合使用是否会使分析产生误差。一般情况下, 研究人员使用平均气温资料时往往认为资料的空间密度愈密愈好, 能更清晰地反映不同地形对气温的影响。但是如果忽略了平均气温资料计算方法不同造成的资料之间的差异, 则可能会在一些分析中产生偏差。如混合使用资料来求取气温网格平均时, 如果不注意偏差的订正, 则计算出的数值在西部可能会偏高, 而东部可能偏低。因此对于资料的空间密度, 要根据实际分析的需要掌握, 如果必须混合使用, 应该对资料之间的差异有所了解, 避免其引起的误差。
(3) 以上分析进一步表明, 在使用气温资料时, 我们要充分重视资料的来源、计算方法、质量状况、台站情况等重要的说明资料的背景资料, 即metadata [16~17]资料。目前国外气候研究人员在使用平均气温资料时, 十分重视metadata资料的情况。由于我国近50年许多站在日平均气温资料计算时方法上有变化, 因此, 在使用我国平均气温资料进行气候分析研究中应该对其给予极大的关注。
4 小结(1) 我国日平均气温的计算值由于4次观测、3次观测不同的计算方法, 造成4次、3次平均值产生一定差异。
(2) 我国平均气温4次与3次差值的平均值在空间分布中具有明显的特征, 西部、北部地区3次平均值偏高; 东南部地区3次平均值偏低。
(3) 平均气温4次与3次差值的年平均值在中西部地区具有扩大的趋势, 是由于最低气温的升高引起的。
(4) 在使用气温平均值时, 要充分重视平均气温值的计算方法, 避免误差。
| [1] | 高国栋, 陆渝蓉编著. 气候学. 北京:气象出版社, 1988. |
| [2] | 章基嘉编著. 气候变化的证据、原因及其器对生态系统的影响. 北京:气象出版社, 1995. |
| [3] | 丁一汇主编.中国的气候变化与气候影响研究.北京:气象出版社,1997.187~191,199~205. |
| [4] | 叶笃正, 曾庆存, 郭裕福主编. 当代气候研究. 气象出版社, 1991: 186–233. |
| [5] | 陈隆勋, 邵永宁, 张清芬, 等. 近四十年我国气候变化的初步分析. 应用气象学报, 1991, 2, (2): 164–173. |
| [6] | 魏凤英, 曹鸿兴, 王丽萍. 20世纪80—90年代我国气候增暖进程的统计事实. 应用气象学报, 2003, 14, (1): 79–86. |
| [7] | 王馥棠. 近十年我国气候变暖影响研究的若干进展. 应用气象学报, 2000, 13, (6): 755–766. |
| [8] | Raino Heino. Metadata and Their Role in Homogendeity.In:Proceedings of the first seminar for homogenization of surface climatological data.1997.5~8. |
| [9] | Karl T R, Williams C N, Young Jr P J, et al. A model to estimate the time of observation bias associated with monthly mean maximum, minimum, and mean temperature for the United States. J Climate Appl Meteor, 1986, 25: 145–160. DOI:10.1175/1520-0450(1986)025<0145:AMTETT>2.0.CO;2 |
| [10] | 中央气象局编定.地面气象观测规范.北京:气象出版社,1979.26~27. |
| [11] | 翟盘茂,任福民.我国最高、最低温度变化规律研究.丁一汇主编.中国的气候变化与气候影响研究.北京:气象出版社,1997.199~206. |
| [12] | 任福民. 1951—1990年中国极端气温变化分析. 大气科学, 1998, 22, (2): 217–227. |
| [13] | 周淑贞,束炯.城市气候学.北京:气象出版社,1994.244~262,418~455. |
| [14] | 张光智王继志, 等. 北京及周边地区城市尺度热岛特征及其演变. 应用气象学报, 2002, 13, (U01): 43–50. |
| [15] | 徐祥德汤绪. 城市化环境气象学引论. 北京: 气象出版社, 2002. |
| [16] | GCOS. Guide to the GCOS Surface and Upper-Air Networks:GSN and GUAN (Version1.0), GCOS Report No. 73. Geneva:WMO, 2002. |
| [17] | WMO. Proposal for a Discovery-level. WMO Metadata Standard. Meeting of expert team on integrated data management. Geneva, 2001. |
 2005, 16 (3): 345-356
2005, 16 (3): 345-356