根据《室外排水设计规范 (GBJ14-87)》 [1]规定, 在进行城市排水管网设计时, 雨水管网和合流制管网的设计排水量, 均应通过本地的城市暴雨强度公式计算, 排水工程的可靠性与采用的暴雨强度公式有直接的关系, 暴雨强度公式是城市雨水排水设计流量的根本依据.
瑞安市位于浙江省东南沿海地区, 地处亚热带季风气候区, 暴雨是该市主要气候灾害之一.据统计, 瑞安市平均每年暴雨日数5.7 d.近年来, 随着沿海经济的腾飞, 瑞安市市政建设迅猛发展, 科学地规划城市发展, 合理地设计市政工程, 是建设部门面临的实际问题.为了配合市政建设的需要, 使市政工程建立在科学的基础上, 本文对瑞安市暴雨强度概率分布及其强度公式进行了研究, 为该市建立科学的城市雨、污分流的管渠系统提供可靠的依据.
1 瑞安市暴雨抽样资料的采样瑞安市气象站成立于1960年, 位于瑞安市城镇范围之内, 配有自记雨量计, 常年进行雨量观测, 迄今共积累了38年的自记雨量记录.本文根据《室外排水设计规范》 [1]和《给水排水设计手册》 [2]中有关编制暴雨强度公式规定, 从瑞安市气象局1965~1997年逐日降水自记曲线上, 按5、10、15、20、30、45、60、90、120 min 9个降水历时挑选并摘录历年最大的若干组雨量数据.
在资料采集过程中, 为了不遗漏历史资料中一些大的降雨强度样本, 同时也为了规范资料采集工作, 规定每年各历时挑选最大的8组雨量数据.本文从瑞安市历史降水自记曲线上共摘录264组数据, 通过计算机信息化处理, 将选出的资料按从大到小顺序排列 (各历时分别进行), 并取前132组数据 (年数的4倍) 构成暴雨抽样基本数据.
2 瑞安市暴雨强度抽样概率分布模式在气象要素概率分布的应用中, 通常根据不同要素特点采用不同的分布模式进行概率曲线的拟合.本文运用耿贝尔 (Gumbel) 分布、指数分布、韦伯 (Weibull) 分布、皮尔逊Ⅲ型分布等概率模式对瑞安市暴雨强度抽样的分布进行讨论, 并根据这些分布模式对暴雨强度资料的拟合情况, 通过对比分析确定用于描述瑞安市暴雨强度抽样分布的概率模式.
2.1 概率分布模式[3](1) 耿贝尔 (Gumbel) 分布
耿贝尔分布的概率密度函数和分布函数分别为:

|
(1) |

|
(2) |
式中y为抽样xi (i=1, 2, ……, N) 的函数, N为抽样数.耿贝尔推得: y=a (xi-b), 其中a > 0, 为尺度参数, b是分布密度的众数.通过积分, 可以求得y的数学期望值和均方差分别为:

|
(3) |

|
(4) |
因此, 由y=a (xi-b), 可以得到:

|
(5) |

|
(6) |
这里mx和ex分别为xi的数学期望和均方差.
分布函数参数确定以后, 通过下式求对应于重现期T的分位数:

|
(7) |
(2) 指数分布
指数分布的概率密度函数和分布函数分别为:

|
(8) |

|
(9) |
式中xi (i=1, 2, ……, N) 为抽样资料, N为抽样数.a表示分布曲线离散程度的参数, r为分布曲线的下限.故对应于重现期T的分位数:

|
(10) |
令1/a=T, 利用抽样的经验概率分布和最小二乘法, 可以计算出系数T、r的估计, 并通过式 (10) 计算各重现期的分位数.
(3) 皮尔逊 (Pearson) Ⅲ型分布
皮尔逊Ⅲ型分布密度函数和分布函数为:

|
(11) |

|
(12) |
式中抽样变量x ≥ 0, 参数T、U ≥ 0分别表示概率曲线的形状和尺度参数, a为概率曲线起点与序列零点的距离.用皮尔逊Ⅲ型分布拟合暴雨强度抽样资料, 首先要对参数T、U、a作估计.根据矩法得到皮尔逊Ⅲ型的数学期望、方差和偏差系数分别为: 



|
(13) |
由于高阶矩误差较大, 因此, 矩法对皮尔逊Ⅲ型参数的估计被认为误差偏大.为了提高估计精度, 可用权函数对参数进行修正, 即:
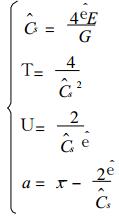
|
(14) |
其中x和



皮尔逊Ⅲ型概率分布模式参数确定后, 则可根据达到某一精度要求的拟合曲线进行各概率或重现期对应的分位数的估算.可以证明皮尔逊Ⅲ型分布曲线某一概率或重现期对应的分位数只依赖于参数T或偏度系数Cs.因此, 给定一个参数T或Cs值后, 就可通过曲线离均系数表, 查算出概率P或重现期T对应的分位数.若对Cs作适当调整, 使拟合误差达到最小, 这便是所谓的“适线法”.
(4) 韦伯 (Weibull) 分布
三参数韦伯分布的概率密度函数和分布函数为:

|
(15) |

|
(16) |
式中b、c > 0及a分别为尺度参数、形状参数和位置参数.当a=0时, 即为二参数Weibull分布.当a=0, c=1时, 即为指数分布.因此, 指数分布可看作韦伯分布的一个特例.这里选用矩法对参数a、b、c作估计.
假设x、e、Cs分别为抽样的平均值、均方差和偏度系数.利用前三阶矩, 通过积分可以求得:

|
(17) |
令

|
(18) |
故重现期T所对应的分位数为:

|
(19) |
暴雨强度抽样分布曲线的拟合是构造暴雨强度公式的一个重要环节, 过去对暴雨强度抽样的拟合常局限于指数分布和皮尔逊Ⅲ型分布.这里利用前述讨论的各概率分布模式及有关模式参数估计方法对瑞安市暴雨抽样进行拟合, 并通过拟合结果的对比分析来评判各种分布模式的适用性, 最终确定暴雨强度公式编制采用的概率模式.对于拟合效果的评判采用均方根误差、相对均方根误差和绝对值误差等最优化准则, 即:

|
(20) |
式中e、f、g分别表示均方根误差、相对均方根误差和绝对值误差; XIi为理论概率模式对应于某一观测经验概率i/(1+N) 的估计值.
表 1为瑞安市暴雨强度抽样各种概率分布模式时的参数估计.表 2为各概率分布模式对暴雨强度抽样拟合指标.从各模式的计算结果来看, 耿贝尔分布对各历时拟合效果不佳, 误差偏大, 该分布模式未被用于暴雨强度公式的构造.指数分布、皮尔逊Ⅲ型分布和韦伯分布的拟合情况较好, 均方根误差和相对均方根误差均小于0.05 mm/min和5%.故认为指数分布、皮尔逊Ⅲ型分布和韦伯分布合适抽样的描述.其中指数分布和皮尔逊Ⅲ型分布对历时抽样的拟合均方根误差, 平均值小于0.03 mm/min, 可见这两种分布模式对暴雨强度抽样的拟合达到了很高的精度.
|
|
表 1 各种概率分布模式的参数估计 |
|
|
表 2 暴雨强度抽样各概率分布模式拟合指标 |
模式参数求出后, 即可确定暴雨强度抽样各概率模式的分布函数, 从而利用分布函数求解各个重现期或某一概率对应的暴雨强度.制作反映暴雨强度、历时、重现期这三者关系的i-t-T表.表 3为暴雨强度抽样指数分布的i-t-T表.
|
|
表 3 指数分布i-t-T表 |
3 瑞安市暴雨强度公式的构造 3.1 非线性模型参数估计
线性模型的参数求解是根据最小二乘法作估计.假设yi、

|
(21) |
由于该式是b0, b1, b2, …, bm的二次函数, 又是非负的, 故其最小值总存在.根据微分学的极值定理, b0, b1, b2, …, bm应是下列联立方程组的解:

|
(22) |
若回归方程是非线性, 则需要根据给出的几组记录值 (xk, yk) (k=1, 2, 3, …, m), 在最小二乘法意义下确定各参数b1, b2, …, bm, 这就要用非线性二乘法来求解, 也即确定参数b1, b2, …, bm, 使f (xk, b1, b2, …, bm) 与yk之间的残差平方和

|
(23) |
为最小.令

|
(24) |
此处bi(0) 是bi的一个初始值.
将f (xk, b1, b2, …, bm) 在点b1(0), b2(0), …, bm(0) 展开为泰勒 (Taylor) 级数, 并略去2次以上的展开项, 得:

|
(25) |
其中

|
(26) |
令

|
(27) |
为了使Q在最小二乘法意义下达到极小, 对上式Δi取偏导数, 并令其等于零, 则有:

|
(28) |

|
(29) |
当近似值bi(0) 及记录值给定后, 根据式 (28) 和 (25) 可确定方程 (27) 的系数矩阵及右端各项.由此可解出Δi, 再按式 (24) 求出bi.当|Δi|值未满足精度要求时, 可用当前的bi代替原来的近似值bi(0), 再重复以上计算, 通过反复迭代, 直到|Δi|值满足预置的允许误差, 此时所获得的bi即为所求的参数.
在计算操作中, 我们采用直接解式 (27) 和最速下降法相结合的方法[4], 即在确定Δi的方程组时, 将式 (27) 改为:

|
(30) |
其中d ≥ 0.当d=0时, 退化为高斯-牛顿法.随着d的增加, Δ的长度趋近于零, 并向ay的方向逼近.由于ay就是Q的最速下降方向, 沿这个方向要求步长不太长, 残差平方和总是减少, 除非Q已经达到极小值.实际计算时, 随迭代过程变化.令d=cTd(0) (T=-1, 0, 1, 2, …), 其中d(0) 表示初值, 通常取d(0)=0.01, c为指定常数 (如取10), T值应尽可能取小, 只需保证解出式 (28)Δi相应的残差平方和有所减少即可.如此反复, 直至Δi的最大值小于允许误差.
3.2 暴雨强度公式的构造现行规范给出的暴雨强度公式形式为:
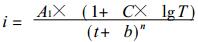
|
(31) |
式中i为暴雨强度 (mm/min), t为降水历时, T为重现期, A1、C、b、n为地方性参数.构造暴雨强度公式, 也就是对式 (31) 中的地方性参数做估计.通常将式 (31) 称做暴雨强度总公式.给定某一重现期, 即式 (31) 分子部分为一参数 (假定为A), 此时公式称做暴雨强度分公式.根据韦伯分布、指数分布、皮尔逊Ⅲ型分布 (模式参数估计采用适线法和权函数法) 得到的瑞安暴雨强度i-t-T表, 利用前述非线性参数估计方法, 求得4套公式的参数估计值.表 4为总公式参数估计值.
|
|
表 4 总公式参数估计值 |
指数分布虽然对暴雨抽样分布的拟合算不上最好, 但通过其编制的暴雨强度公式的精度往往好于其它的分布模式.可见, 某个概率模式对暴雨强度抽样拟合精度的提高, 并不说明其对应的暴雨强度公式拟合的精度也会得到相应提高.从总公式拟合的均方根误差来看, 由适线法、权函数法作参数估计的皮尔逊Ⅲ型分布所对应的公式拟合误差分别为0.0673和0.0790;韦伯分布、指数分布的公式误差分别为0.0748和0.0507.因此, 指数分布对构造瑞安市暴雨强度公式不仅适用, 而且拟合精度明显高于其它分布, 故被选为最终用于构造公式的分布模式.表 5和式 (32) 分别为通过指数分布i-t-T表得到的暴雨强度分公式和总公式, 其中总公式的均方根误差为0.0507 (见表 4).
|
|
表 5 瑞安市暴雨强度分公式 |
瑞安市暴雨强度总公式:

|
(32) |
暴雨强度公式编制首先是选择适当的概率模式对抽样资料进行拟合并计算出i-t-T表; 然后在i-t-T表基础上, 利用非线性模型参数估计确定暴雨强度公式中的参数, 即构造各重现期与暴雨强度之间的经验公式.关于暴雨公式中的参数估计, 常用回归法、摆试法、线性最小二乘法等方法.本文在制定非线性模型的参数估计算法中, 为提高参数迭代求解的效率利用了最速下降法, 对计算步骤和算式做了精心设计与编程.在采用差商方法求偏导数时, 利用计算机语言中具有高位精度的扩展型实数来处理, 以使误差控制在很小的范围内, 保证公式参数估计的精度.因此瑞安市暴雨强度公式达到了较高的精度.
| [1] | 中华人民共和国国家标准.室外排水设计规范, GBJ14-87, 1988. |
| [2] | 给水排水设计手册 (第五册).北京:中国建筑工业出版社, 1985, 48~87. |
| [3] | 马开玉, 丁裕国, 屠其璞, 等. 气候统计原理与方法. 北京: 气象出版社, 1993: 391-419. |
| [4] | 钱焕延. 计算方法. 上海: 上海交通大学出版社, 1988: 297-312. |
 2000, 11 (3): 355-363
2000, 11 (3): 355-363






