2. 海军驻上海地区第四代表室,上海 201108
2. Fourth Representative Office of the Navy in Shanghai, Shanghai 201108, China
发动机的配气过程对发动机缸内的燃烧工作过程有较大影响。为了保证和提高配气质量,配气阀应适当地调节开启及关闭的时刻,以实现最佳配气正时,提高充量系数,减少将泵气损失[1]。全可变配气技术打破传统柴油机受凸轮型线制约的瓶颈[2],可以柔性调节气阀配气参数,实现全可变配气,改善柴油机任意工况下的性能[3]。本文搭建缸内配气充量模型对柴油机不同工况下的最佳配气充量以及最佳配气充量下的气阀运动最优配气参数进行计算,以此来提高柴油机的做功能力和效率[4]。
1 缸内配气充量数学模型对于全可变配气柴油机可变配气过程来说,配气过程的动力学方程是在质量守恒定律和理想气体状态方程的基础上得到的[5]。新鲜空气在配气管内的流动可以视为作稳定流动。稳定流动中,任意一截面的一切参数都不随时间的变化而改变,因此,流过某一截面的质量流量为常数[6]。由于空气的密度较小,进气管的位置变化也不大,因此,新鲜空气位能变化极小,可以忽略不计。并且新鲜空气在流动过程中,由于进气时间相对较短,空气与进气管的热量交换也可以忽略不计,可视为绝热流动。空气在进气管也不对外做功[7],任意截面上空气的焓值与其动能之和保持不变,服从稳定流动的能量方程:
| $ {h}_{\text{0}}={h}_{1}+\frac{{c}_{1}{}^{2}}{2}={h}_{2}+\frac{{c}_{2}{}^{2}}{2}={\text{C}} $ | (1) |
式中:
由式(1)整理可得任意一截面空气的流速方程为
| $ {c_1} = {\left( {2\left( {{h_0} - {h_1}} \right)} \right)^{\frac{1}{2}}} $ | (2) |
依据理想气体状态方程:
| $ p \cdot v = R \cdot T $ | (3) |
以及绝热过程方程:
| $ p\cdot {v}^{\gamma }={\text{C}} $ | (4) |
式中:
将初态和终态的压力、比体积、温度及理想气体状态方程式(3)代入式(4),得出初态和终态温度比与其压力比之间的关系:
| $ \frac{{{T_1}}}{{{T_0}}} = {\left( {\frac{{{p_1}}}{{{p_0}}}} \right)^{\frac{{\gamma - 1}}{\gamma }}} $ | (5) |
在绝热过程中,初态和终态的焓差可以用温度差方程来表示:
| $ {h_0} - {h_1} = {c_p}\left( {{T_0} - {T_1}} \right) $ | (6) |
因此,任意一截面的流速方程还可以表示为
| $ {c_1} = {\left( {2\left( {{h_0} - {h_1}} \right)} \right)^{\frac{1}{2}}} = {\left( {2{c_p}\left( {{T_0} - {T_1}} \right)} \right)^{\frac{1}{2}}} $ | (7) |
由于理想气体满足:
| $ {c_p} = \frac{{\gamma \cdot R}}{{\gamma - 1}} $ | (8) |
最终,气体的流速可以用初、终态的相关参数表达:
| $ \begin{aligned} & {c_1} = {\left( {2\frac{{\gamma \cdot R}}{{\gamma - 1}}\left( {{T_0} - {T_1}} \right)} \right)^{\frac{1}{2}}} \hfill= \\ & {\left( {{\text{2}}\frac{{\gamma \cdot R \cdot {T_0}}}{{\gamma - 1}}\left( {1 - {{\left( {\frac{{{p_1}}}{{{p_0}}}} \right)}^{\frac{{\gamma - 1}}{\gamma }}}} \right)} \right)^{\frac{1}{2}}} \hfill \\ \end{aligned} $ | (9) |
稳定流动中,根据质量守恒定律,任意一截面的质量流量方程为
| $ {m_1} = \frac{{{A_1} \cdot {c_1}}}{{{V_1}}} $ | (10) |
将
| $ {m_1} = {A_1}{\left( {2\frac{\gamma }{{\gamma - 1}}\frac{{{p_0}}}{{{V_0}}}\left[ {{{\left( {\frac{{{p_1}}}{{{p_0}}}} \right)}^{\frac{2}{\gamma }}} - {{\left( {\frac{{{p_1}}}{{{p_0}}}} \right)}^{\frac{{\gamma + 1}}{\gamma }}}} \right]} \right)^{\frac{1}{2}}} $ | (11) |
式中:
由质量流量方程可以看出某一截面的质量流量与初态、终态的状态参数和气体的流通面积有关。
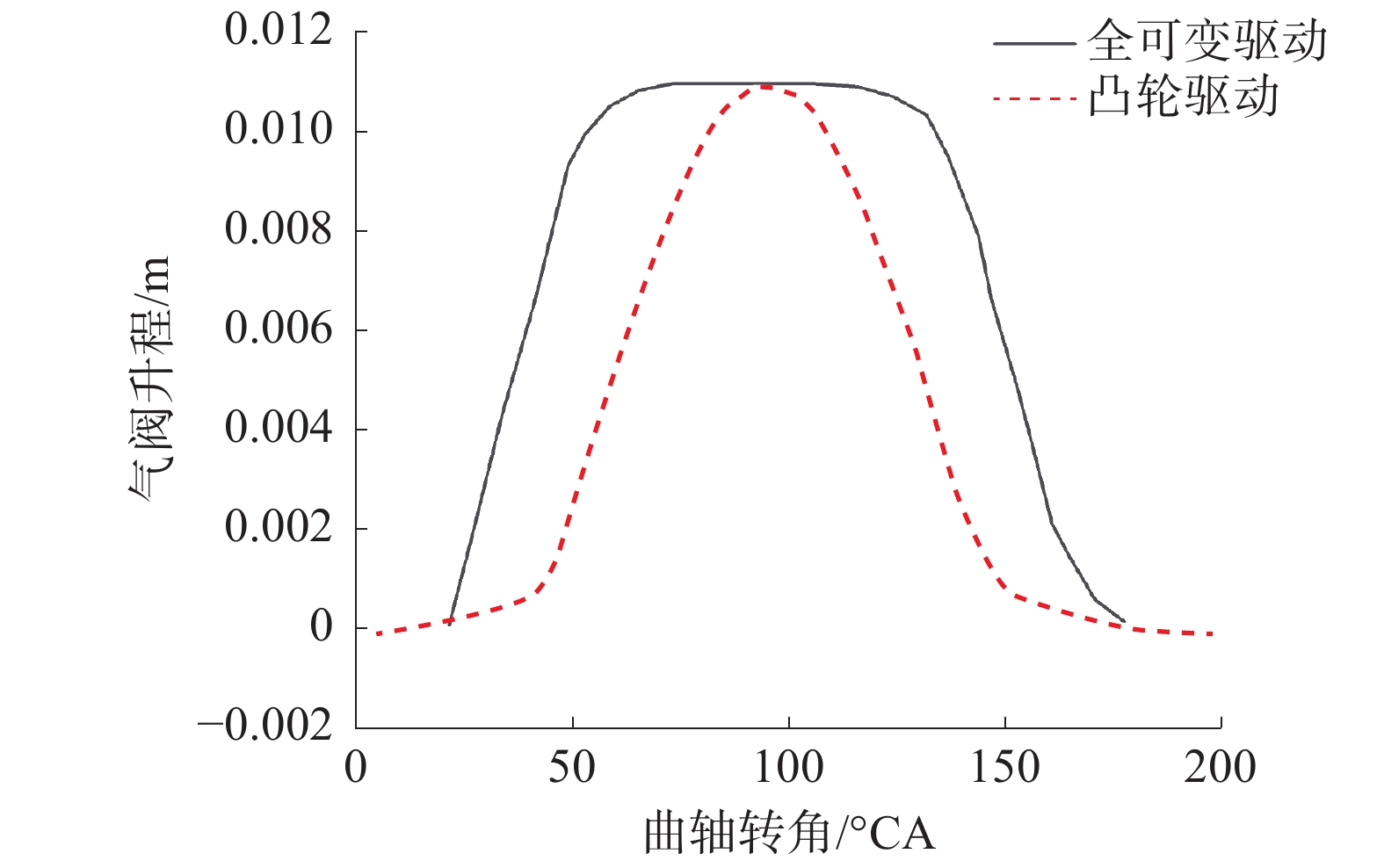
图1为凸轮驱动配气机构与全可变驱动配气机构的气阀升程曲线图。
|
Download:
|
| 图 1 气阀升程曲线 | |
通过图1可看出电液全可变配气机构的充气效率明显优于凸轮驱动配气机构[8]。柴油机配气过程中配气充量的数学模型建立在质量守恒定律和理想气体状态方程的基础上。在配气过程中,配气管的温度和新鲜空气温度的差异可以忽略[9]。根据理想气体状态方程,将气缸内的压力对时间求导获得气缸内压力方程:
| $ \frac{{{\rm{d}}{p_{\rm{c}}}}}{{{\rm{d}}t}} = \frac{1}{{{V_{\rm{c}}}}}\left[ {R \cdot T\mathop {\mathop { \cdot {m_{\rm{c}}}}\limits^ \bullet - \mathop {\mathop {{V_{\rm{c}}} \cdot }\limits^ \bullet {p_{\rm{c}}}} } } \right] $ | (12) |
式中:
对于自然吸气柴油机来说,气缸内初始压力等于排气背压,气缸内的体积随曲轴转角变化的表达式为
| $ {V_{\rm{c}}}\left( \theta \right) = \frac{{{V_{\rm{d}}}}}{2}\left( {1 - \cos \theta } \right) + {V_{\rm{u}}} $ | (13) |
| $ \theta = \left( {\int_0^t {\frac{N}{{60}} \cdot 360 \cdot {\rm{d}}t} } \right)\boldsymbolod {720^ \circ } $ | (14) |
式中:
配气阀开启过程中,新鲜空气理想的质量流量可根据稳定流动的流量计算式(11)获得[10]:
| $\dot m = {A_{\rm{v}}} \cdot {d_0}\left( {{p_{\rm{c}}},{p_{\rm{m}}},{T_{\rm{c}}},{T_{\rm{m}}}} \right)$ | (15) |
式中:
气阀某一时刻的有效流通面积与气阀升程有关,它们之间的函数关系为
| $ {A_{\rm{v}}}\left( {{L_{\rm{v}}}} \right) = Z \cdot {\text π} \cdot {L_{\rm{v}}}\cos \beta \left[ {{d_{\rm{v}}} + {L_{\rm{v}}} \cdot \sin \beta \cdot \cos \beta } \right] $ | (16) |
式中:
气阀流量函数可根据稳定流动的流量计算式(11)表达为[11]
| $ {d_0}\left( {{p_{\rm{c}}},{p_{\rm{m}}},{T_{\rm{c}}},{T_{\rm{m}}}} \right) = \left\{ \begin{aligned} & \frac{{{p_{\rm{m}}}}}{{{{\left( {R \cdot {T_{\rm{m}}}} \right)}^{\frac{1}{2}}}}} \cdot {\psi _{\text{0}}} \cdot \left( {\frac{{{p_{\rm{c}}}}}{{{p_{\rm{m}}}}}} \right),{p_{\rm{c}}} \leqslant {p_{\rm{m}}} \hfill \\ & \frac{{{p_{\rm{c}}}}}{{{{\left( {R \cdot {T_{\rm{c}}}} \right)}^{\frac{1}{2}}}}} \cdot {\psi _{\text{0}}} \cdot \left( {\frac{{{p_{\rm{m}}}}}{{{p_{\rm{c}}}}}} \right),{p_{\rm{c}}} > {p_{\rm{m}}} \end{aligned} \right. $ | (17) |
| $ {\psi _{\text{0}}}\left( x \right) = \left\{ \begin{aligned} & {\gamma ^{\frac{{\text{1}}}{{\text{2}}}}}{\left( {\frac{2}{{\gamma + 1}}} \right)^{\frac{{\gamma + 1}}{{2\left( {\gamma - 1} \right)}}}},x \leqslant {\gamma _{\rm{c}}} \hfill \\ & {x^{\frac{1}{2}}}{\left( {\frac{{2\gamma }}{{\gamma - 1}}\left( {1 - {x^{\frac{{\gamma - 1}}{\gamma }}}} \right)} \right)^{\frac{1}{2}}},x > {\gamma _{\rm{c}}} \end{aligned} \right. $ | (18) |
| $ {\gamma _{\rm{c}}} = {\left( {\frac{2}{{\gamma + 1}}} \right)^{\frac{\gamma }{{\gamma - 1}}}} $ | (19) |
式中:
由于进气管的压力近似等于标准大气压,将上述配气模型作进一步简化:进气管内的压力为
传统凸轮轴驱动气阀机构的气阀升程曲线取决于凸轮型线,而全可变驱动的柴油机的气阀升程曲线可以由进气阀开启时刻、气阀升程、气阀开启持续期及气阀开启速度来表达,其气阀升程曲线方程组[12]如式(20):
| $ \begin{aligned} &\qquad\qquad\qquad {{{L}}_{\rm{v}}}\left( {{t_{{\rm{IVO}}}},{\rm{IVL}},{t_{{\rm{IVD}}}},t} \right) = \\ & \left\{ \begin{aligned} & {{\rm{s}}_r}\left( {t - {t_1}} \right),\quad\quad{t_1} \leqslant t < {t_2}\\ & L - {L_s}\exp \left( { - \frac{{{s_r}}}{{{L_s}}}\left( {t - {t_2}} \right)} \right),\quad\quad{t_2} \leqslant t < {t_3}\\ & L - {L_s}\exp \left( { - \frac{{{s_c}}}{{{L_s}}}\left( {\frac{s}{2} - \left( {t - {t_3}} \right)} \right)} \right),\quad\quad{t_3} \leqslant t < {t_4}\\ & {\rm{ - }}{s_c}\left( {t - t_4^{}} \right) + \left( {1 - \lambda } \right){\rm{IVL}},\quad\quad{t_4} \leqslant t < {t_5}\\ & {s_s}\left( {t - {t_5}} \right) + {s_s}{d_s},\quad\quad{t_5} \leqslant t < {t_6}\\ & 0,\quad\quad{\rm{其他}} \end{aligned} \right. \end{aligned} $ | (20) |
式中:
实际新鲜空气的质量流量
| $ {{\mathop m\limits^ \bullet} _c} = \mu \mathop m\limits^ \bullet $ | (21) |
许多类型的的发动机,流量系数
| $ \mu = f\left( {{L_v}} \right) $ | (22) |
由于发动机的结构千差万别,导致流量系数
| $ \mu = 0.98 - 0.33{\left( {\frac{{{L_v}}}{{{d_v}}}} \right)^2} $ | (23) |
因此进入气缸内新鲜充量是质量流量在气阀开启持续期内的积分,表达式为
| $ m = \int_{{t_{{\rm{IVO}}}}}^{{t_{{\rm{IVO}} + {\rm{IVD}}}}} {{{\mathop m\limits^ \bullet }_c}} {\rm{d}}t $ | (24) |
式(12)~(24)是发动机气缸内配气充量的数学模型,根据此模型可以获得发动机在不同转速情况下的配气充量。
2 配气充量模型模块化实现基于Simulink仿真软件搭建全可变驱动气阀柴油机缸内配气充量数学模型,并开展仿真研究。
2.1 配气充量数学模型的搭建本文以东风朝阳柴油机厂4102系列柴油机为研究对象,开展全可变配气背景下的缸内充量研究。此系列柴油机为四缸柴油机,缸径为102 mm,行程为118 mm,额定功率为49/2 300 kW/(r·min−1),最大扭矩/转速为235/1 600 N·m/(r·min−1),全负荷最低燃油消耗率为238 g/(kW·h),配气门提前开启位置上止点前 14 °CA,配气门延迟关闭位置下止点后 50°CA,排气门提前开启位置下止点前 56°CA,排气门延迟关闭位置上止点后 16°CA,压缩比为17.5∶1,气阀座喉口直径为40 mm,气阀座锥角为45°,配气阀阀杆直径危机10 mm,每缸配气阀1个。
利用Simulink模块化设计功能[13],全可变配气模型分为缸内体积模型、缸内压力模型、气阀升程模型、气阀有效流通面积模型、气阀流量函数模型、气阀质量流量模型[14]。搭建后的全可变配气充量计算整体模型如图2所示。

|
Download:
|
| 图 2 全可变配气模型 | |
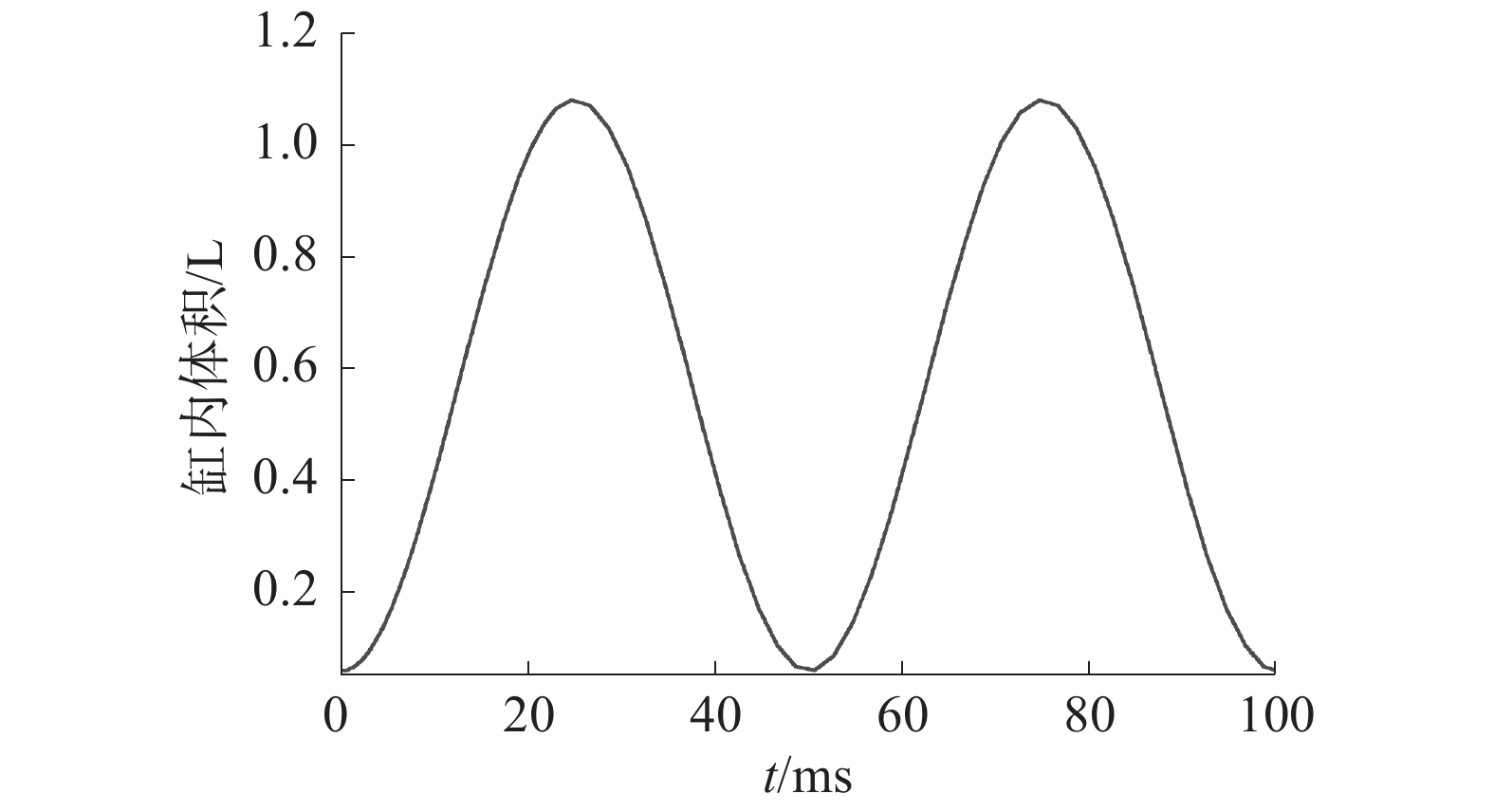
在1 200 r/min工况下,仿真得到模型曲线如图3,可以看出缸内体积变化的范围是从活塞上止点到活塞下止点。
|
Download:
|
| 图 3 体积变化曲线 | |
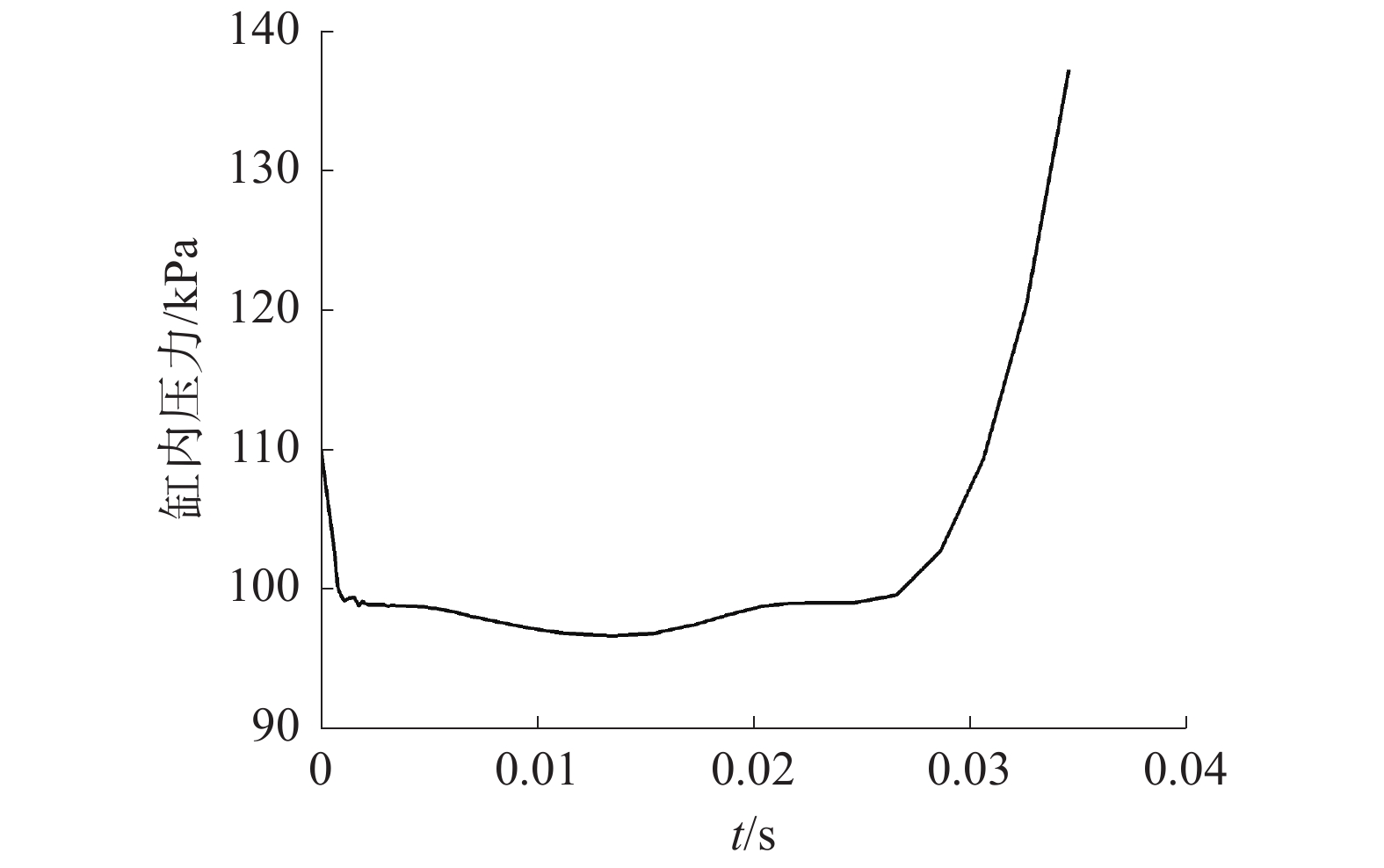
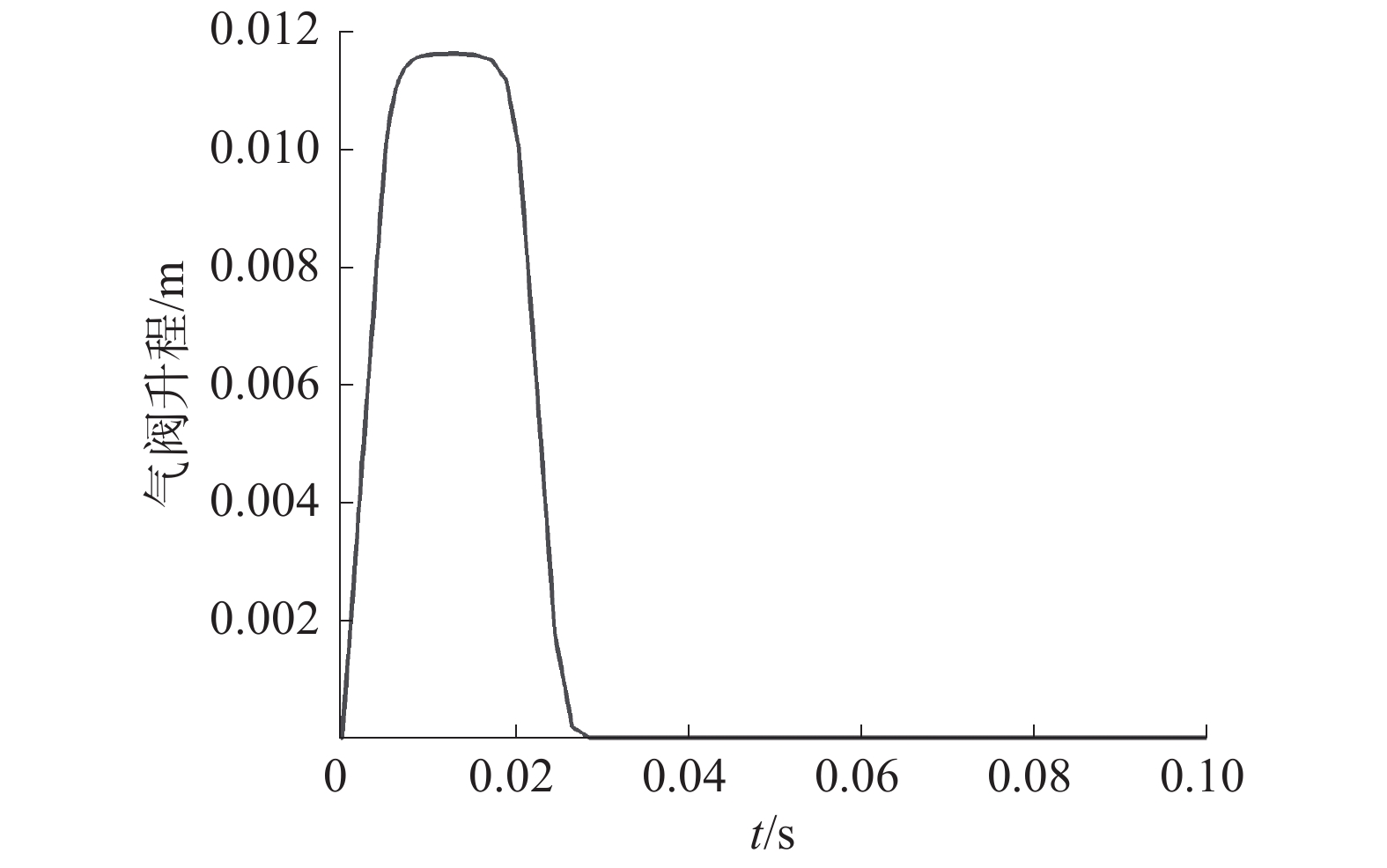
由图4缸内压力变化曲线可以看出,进气阀开启时刻缸内压力由于体积变大迅速降低。新鲜空气吸入时,缸内压力有一段平稳状态,近似等于外界大气压,随着压缩冲程的开始,缸内气压极速上升。由图5气阀升程变化曲线可以看出,该模型输出的气阀运动曲线符合全可变配气机构的气阀升程曲线变化规律。
|
Download:
|
| 图 4 配气过程缸内压力变化曲线 | |
|
Download:
|
| 图 5 气阀升程曲线 | |
由图6可以看出,在进气阀开启初期,质量流量是负值,说明缸内气体倒流入进气管中。因为进气阀开启时,缸内的压力大于进气管内的压力,在压力差的作用下,缸内气体流入进气管内。随着气阀升程逐渐增大,空气的质量流量也缓慢变大,到达峰值后,进气阀关闭,气阀升程逐渐减小,空气质量流量也变小,气阀关闭后质量流量变为零。

|
Download:
|
| 图 6 气阀质量流量变化曲线 | |
图7是全可变配气柴油机同一转速下,升程可变的质量流量曲线。可以看出随着气阀升程逐渐增大,流过气阀的空气质量流量也随之增大。说明在气阀升程未达到饱和值11.6 mm时,随着升程变大,气阀有效流通面积增大,为新鲜空气进入气缸提供了较好的流通条件,促使质量流量增加。
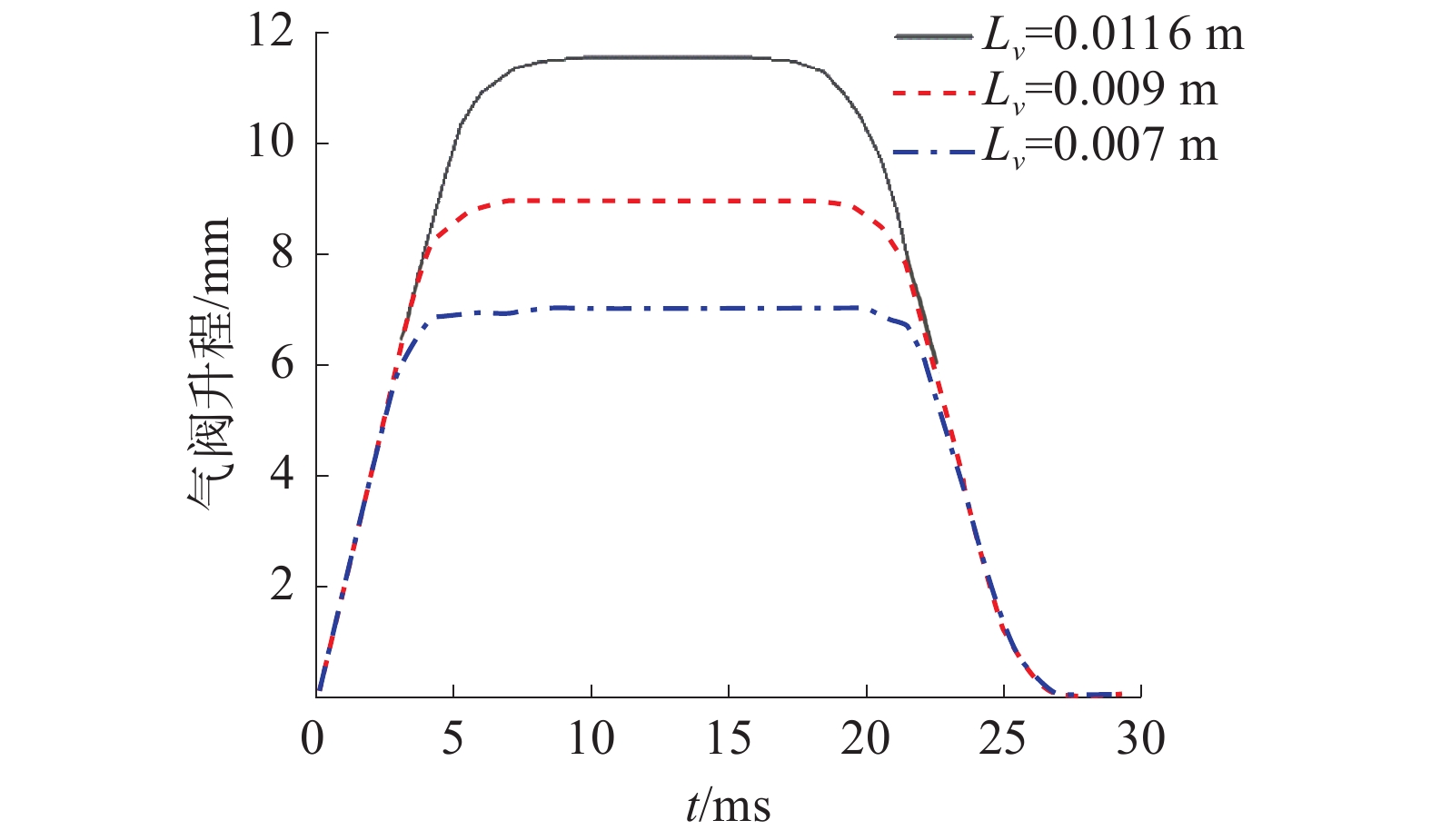
|
Download:
|
| 图 7 升程可变的气阀曲线 | |
图8是全可变配气柴油机同一转速下,升程可变的气阀升程曲线。可以看出气阀升程增大,气阀有效流通面积随之增大。这样有利于更多的新鲜空气流入柴油机气缸内,提高柴油机的充气效率,为缸内燃油的燃烧提供充足的新鲜空气,改善柴油机的燃烧。由表1可知,对计算结果进行了分析,得到的结论是随着柴油机转速逐渐增大,柴油机缸内配气充量先缓慢增大在2000 r/min附近达到峰值,随后缓慢减小。柴油机每一工作循环,新鲜空气充入气缸内的质量约为1.11 g,充量系数约为1.06,在最低喷油量的情况下,过量空气系数约为1.80。
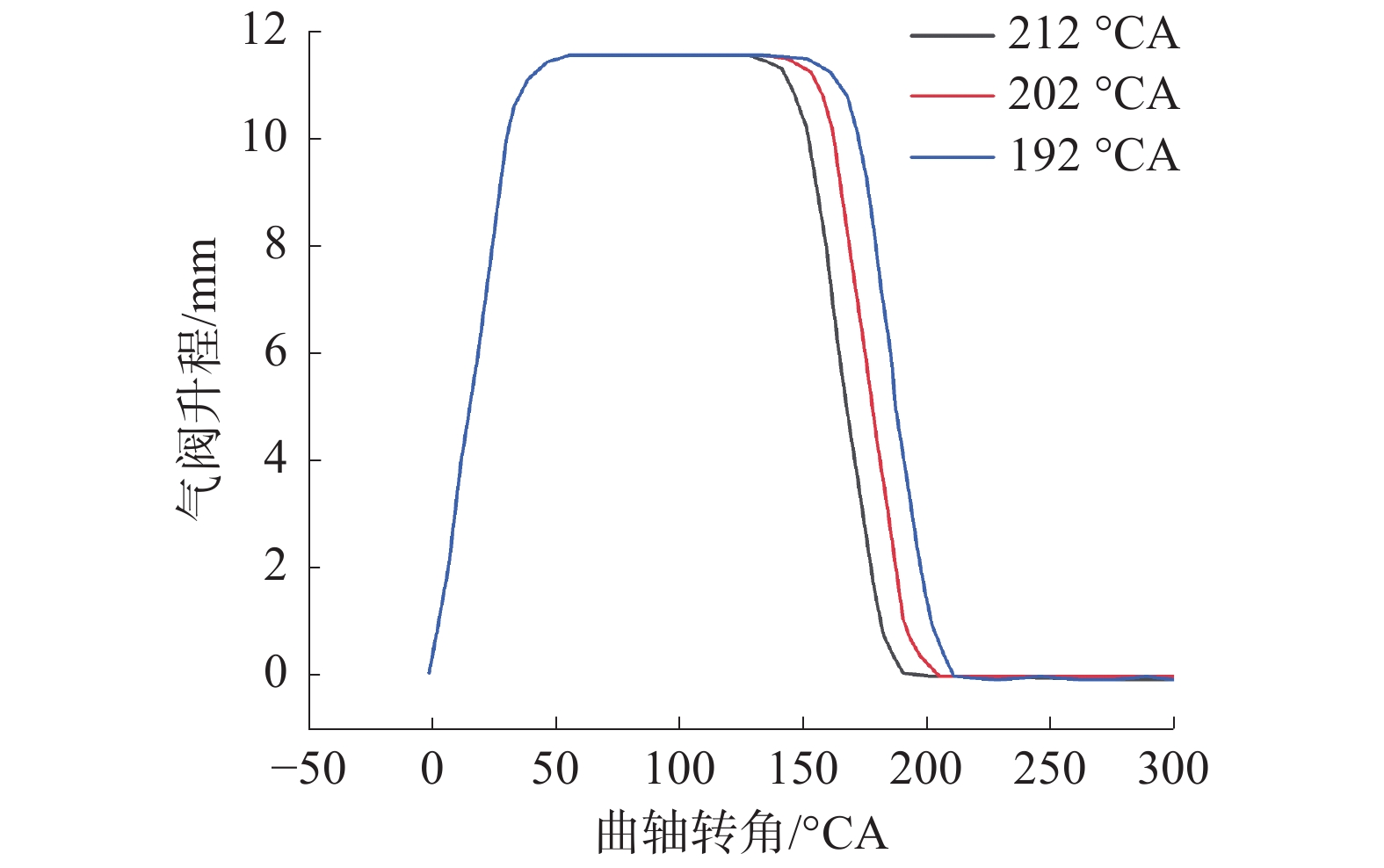
|
Download:
|
| 图 8 气阀开启持续期可变的气阀升程曲线 | |
|
|
表 1 不同转速下柴油机配气充量、配气参数及结果分析 |
在4102系列柴油机的相关参数基础上利用GT-power软件建立模型,以此模型对上节中Simulink仿真结果进行验证分析[15]。CY4102BG柴油机的GT-power模型见图9。

|
Download:
|
| 图 9 4102系列柴油机的GT-power模型 | |
柴油机转速为700~2 400 r/min,步长为100 r/min,设置为18个工况,并选取了其中的5个工况,得到缸内进气质量情况变化如图10、11。如图11,转速从700 r/min到2 400 r/min增大的过程中除个别点外,气缸内每循环流入的空气质量先逐步增大,到2 000 r/min时达到峰值,随后逐渐减小。通过表2 GT-power模型的验证结果也可以得出先前搭建的Simulink模型具有良好的准确度,可以作为柴油机参数优化的模型依据。
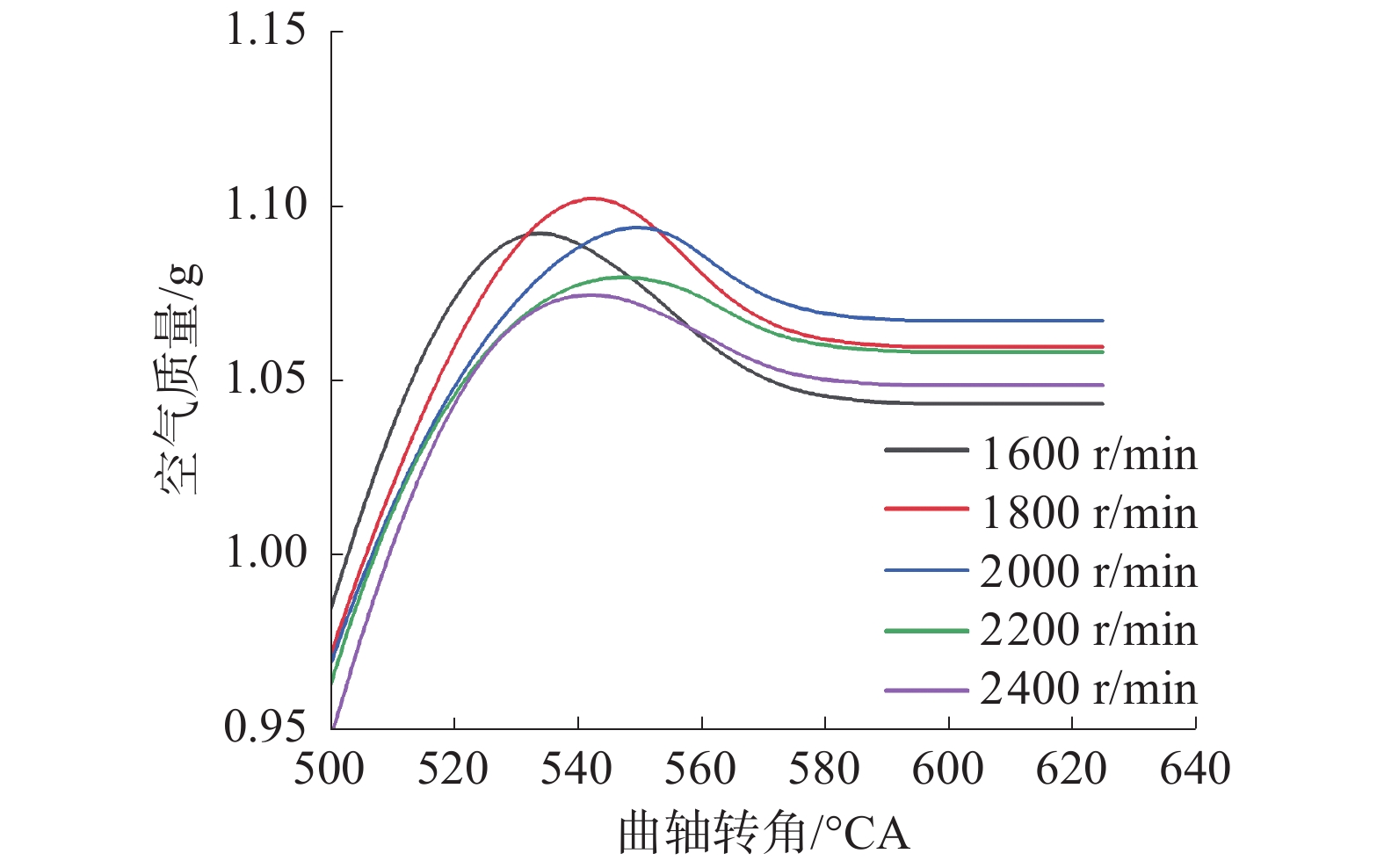
|
Download:
|
| 图 10 气缸每循环流入空气总质量曲线 | |
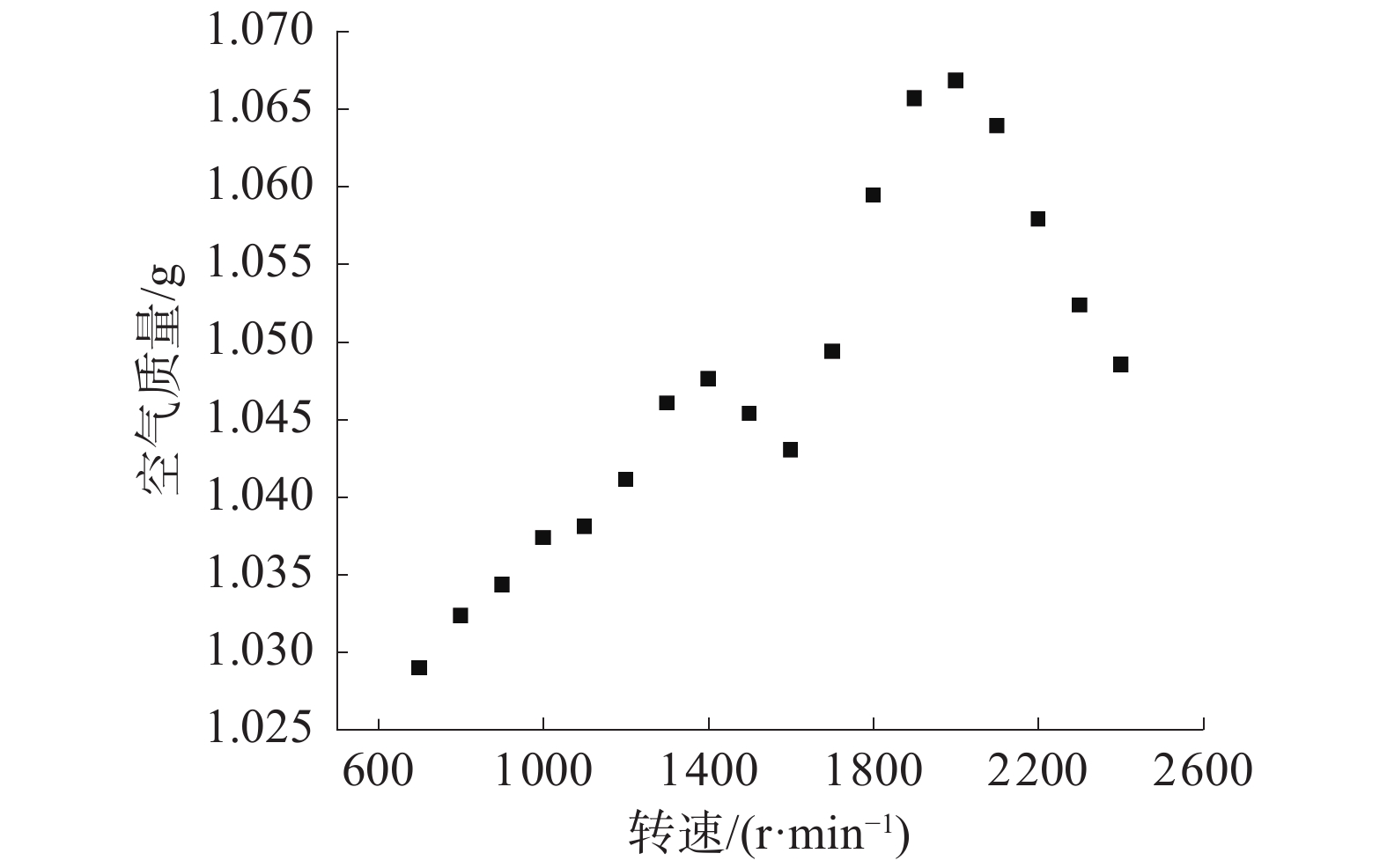
|
Download:
|
| 图 11 不同case下气缸内每循环流入空气质量 | |
|
|
表 2 不同转速下模型误差分析 |
1)在4102柴油机相关参数的基础上,建立了全可变配气柴油机缸内配气充量的数学模型,相关模型和方法为柴油机缸内充量优化提供参考。
2)利用Simulink搭建了全可变配气柴油机缸内配气充量的数学模型,计算了不同转速下的最大配气充量,结果分析表明:随着柴油机转速逐渐增大,柴油机缸内配气充量先缓慢增大在2000 r/min附近达到峰值,随后缓慢减小。柴油机每一工作循环,新鲜空气充入气缸内的质量约为1.11 g,充量系数约为1.05,在最低喷油量的情况下,过量空气数约为1.80。
3)利用GT-power软件建立模型,对Simulink仿真结果进行验证分析,从验证结果中可知,搭建的Simulink模型具有较好的准确度,为全可变配气柴油机气阀参数优化及增大缸内充量系数提供了理论依据。
| [1] |
苏岩, 李理光, 肖敏, 等. 可变配气相位对发动机性能的影响[J]. 汽车技术, 2000(10): 10-14. DOI:10.3969/j.issn.1000-3703.2000.10.004 ( 0) 0)
|
| [2] |
哈菲, 史楠. 发动机可变配气技术及发展[J]. 湖北农机化, 2019(24): 64. DOI:10.3969/j.issn.1009-1440.2019.24.059 ( 0) 0)
|
| [3] |
路勇, 李建, 李博, 等. 发动机电液全可变配气系统建模与同步仿真[J]. 哈尔滨工程大学学报, 2017, 38(7): 1129-1134. ( 0) 0)
|
| [4] |
郑宇, 孟凡旺, 张强. 配气正时对增压发动机性能影响综述[J]. 内燃机与配件, 2019(15): 52-55. DOI:10.3969/j.issn.1674-957X.2019.15.025 ( 0) 0)
|
| [5] |
刘树臣. 车用发动机连续可变配气系统的设计与动力学分析[D]. 济南: 山东大学, 2009.
( 0) 0)
|
| [6] |
GILLELLA P, SUN Zongxuan. Design, modeling, and control of a camless valve actuation system with internal feedback[J]. IEEE/ASME transactions on mechatronics, 2011, 16(3): 527-539. DOI:10.1109/TMECH.2010.2045656 ( 0) 0)
|
| [7] |
刘威. 柴油机连续可变气门驱动系统研究[D]. 大连: 大连理工大学, 2018.
( 0) 0)
|
| [8] |
杨靖, 王子昌, 王毅, 等. 电控液压全可变气门驱动系统的设计与分析[J]. 湖南大学学报(自然科学版), 2017, 44(2): 9-15. ( 0) 0)
|
| [9] |
刘波澜, 余锡洋, 王晓刚, 等. 凸轮驱动的液压全可变气门机构研究[J]. 北京理工大学学报, 2020, 40(9): 935-940. ( 0) 0)
|
| [10] |
LI Huan, HUANG Ying, ZHU G G, et al. Profile tracking for an electro-hydraulic variable valve actuator using receding horizon LQT[J]. IEEE/ASME transactions on mechatronics, 2019, 24(1): 338-349. DOI:10.1109/TMECH.2019.2892038 ( 0) 0)
|
| [11] |
BEHRE L, MERCORELLI P. Sensing of the engine cylinder valves motion[J]. Proceedings, 2017, 1(2): 26. ( 0) 0)
|
| [12] |
王丁, 陈新记, 王胜. 电液无凸轮发动机气门结构设计与研究[J]. 机床与液压, 2019, 47(20): 160-163. DOI:10.3969/j.issn.1001-3881.2019.20.037 ( 0) 0)
|
| [13] |
乔英志. 4190型柴油机工作过程仿真与性能优化[D]. 厦门: 集美大学, 2013.
( 0) 0)
|
| [14] |
王纪元. 柴油机工作过程的Simulink建模仿真研究[D]. 大连: 大连理工大学, 2008.
( 0) 0)
|
| [15] |
韩伟强, 李博仑, 潘锁柱, 等. 电液全可变气门工作周期的划分及特征时间与占比变化规律的研究[J]. 机械工程学报, 2017, 53(12): 201-208. ( 0) 0)
|
 2021, Vol. 48
2021, Vol. 48


