水下航行器所受流体阻力的大小直接影响其航速以及能源消耗速度。目前主要的流体减阻技术有沟槽表面减阻技术^[1]、低表面能减阻技术^[2]、微气泡减阻技术^[3]和外加射流减阻技术^[4]等。但是从水下航行器的实际工程应用角度来看，很多减阻技术因为减阻机理不明确、使用维护困难等制约因素而不适合用于航行器的流体减阻上。因此提出一种新型而有效的减阻结构具有重要意义。

柔性表面减阻技术起源于研究人员对海豚皮肤的仿生研究^[5]，指的是在水下航行器外壳上敷设一层柔性蒙皮，柔性蒙皮会随着来流产生相应的形貌变化，进而产生减阻效果。值得注意的是，柔性表面减阻技术虽然能起到一定的减阻效果，但由于其表面减阻的结构参数通常来源于自然界中动植物表面特定的连续性几何形貌，导致减阻表面抽象度低、在实际工程中应用难度大以及结构参数设定具有一定盲目性等问题，不便于对研究对象进行减阻特性的深入研究。

近年来，双层隔振系统广泛应用于舱室内的减振研究中^[6]，双层隔振系统是在单层隔振系统的基础上增加一个中间质量块及一层弹性支撑形成的，即双层隔振系统由2层弹簧阻尼隔振器和隔振器之间的中间质量块组成。相比于单层隔振系统，双层隔振系统能在较宽的频率范围内发挥更好的减振效果，现已被广泛应用在汽车、航天和船舶等领域，是振动控制系统研究的重点领域。

本文针对减小水下航行器阻力问题，考虑到当前表面减阻技术的局限性以及双层隔振系统的广泛应用，将柔性表面减阻技术和微小化、阵列化的双层隔振系统相结合，提出一种新型的双层柔性蒙皮结构。针对此结构复杂且具有大变形的特点，本文通过基于浸入边界法的程序框架IB2d^[7-8]建立仿真模型，并对其进行数值计算，以研究双层柔性蒙皮各结构参数对减阻性能的影响。

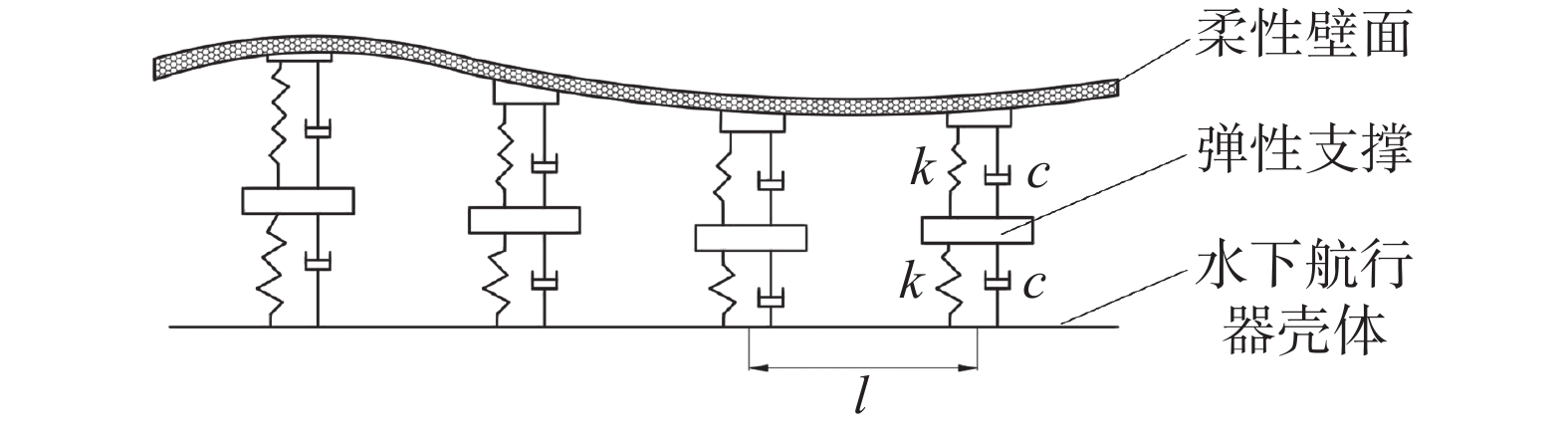
1 双层柔性蒙皮模型及控制方程 1.1 双层柔性蒙皮物理模型

本文设计的柔性蒙皮结构由柔性壁面和弹性支撑组成，弹性支撑则是由中间质量块和上下层弹簧及阻尼构成，其物理模型如图1所示。

双层柔性蒙皮外层的柔性壁面一方面作为传统柔性蒙皮发挥流体减阻作用，另一方面发挥约束作用，用以固定弹性支撑。

1.2 浸入边界法的控制方程

双层柔性蒙皮结构复杂且存在大变形问题，常规的数值方法在处理这类问题时，需要生成复杂的贴体网格，且需要不断在新旧网格上交换各种数据。这两方面不但加大了计算量，而且降低了仿真计算的精度和稳定性。浸入边界法通过在N-S方程上附加一个体积力项来表示固体对流体的影响，无需生成复杂的贴体网格，大大简化了计算过程，适合对双层柔性蒙皮进行仿真计算。

浸入边界法控制方程以N-S方程为出发点，描述了具有惯性的牛顿流体的运动。包括双层柔性蒙皮和流体在内的整个物理区域，都假定为不可压缩牛顿流体的黏性流动，其连续性和动量方程可分别表示为

$ \begin{split} & \rho \left(\dfrac{{\partial {{u}}({{x}},t)}}{{\partial t}} + {{u}}({{x}},t) \cdot \nabla {{u}}({{x}},t)\right) = -\nabla p({{x}},t)+\\ & \quad\quad\quad\quad\quad\quad \mu \Delta {{u}}({{x}},t) + {{f}}({{x}},t) \end{split} $

(1)

$ \nabla \cdot {{u}}({{x}},t) = 0 $

(2)

式中： $\rho $ 为流体的密度； ${{u}}({{x}},t) = (u({{x}},t),v({{x}},t))$ 为欧拉描述下的流体速度矢量； $p({{x}},t)$ 为流体压力； ${{f}}({{x}},t)$ 为双层柔性蒙皮的单位力浸入边界施加到流体上的体积力；自变量是位置 ${{x}} = (x,y)$ 和时间 $t$ 。

式(1)等价于流体的动量守恒，而式(2)则是要求流体不可压缩的条件。

流体与双层柔性蒙皮浸入边界之间的相互作用方程为

$\begin{array}{l} {{f}}({{x}},t) = \displaystyle\int {{{F}}(r,t)\delta ({{x}} - {{X}}(r,t)){\rm{d}}r} \end{array} $

(3)

$ \begin{array}{l} {{U}}({{X}}(r,t),t) = \dfrac{{\partial {{X}}(r,t)}}{{\partial t}} = \displaystyle\int {{{u}}({{x}},t)\delta ({{x}} - {{X}}(r,t)){\rm{d}}{{x}}} \end{array}$

式中： ${{X}}(r,t)$ 为拉格朗日参数 $r$ 标记的材料点在时间 $t$ 的笛卡尔坐标； ${{F}}(r,t)$ 为双层柔性蒙皮浸入边界中的弹性变形对函数施加到流体上的每单位面积的力的拉格朗日位置 $r$ 和时间 $t$ 的乘积。式(3)中的欧拉力 ${{f}}({{x}},t)$ 定义在整个流体域 $\varOmega $ 上，而拉格朗日力 ${{F}}(r,t)$ 定义在双层柔性蒙皮浸入边界上。

正则化的增量函数为

$ {\delta _h}({{x}}) = \frac{1}{{{h^3}}} \phi \left(\frac{{{x_1}}}{h}\right) \phi \left(\frac{{{x_2}}}{h}\right) $

式中：h为流体网格宽度； $\mathop {\phi (r)}\limits^{} $ 的表达式为

$ \mathop {\phi (r)}\limits^{} = \left\{ \begin{array}{l} \dfrac{1}{4}\left(1 + \cos \left(\dfrac{{{\rm{ {\text{π}} }}r}}{2}\right)\right),\;\;\;\;\left| r \right| \leqslant 2 \\ 0,\;\;\;\;{\rm{{\text{其他}}}} \end{array} \right. $

基于浸入边界法控制方程的离散空间上采用的是有限差分法，时间上采用的是基于中点规则的二阶龙格–库塔方法，具体离散过程参见文献[9]。

1.3 双层柔性蒙皮仿真模型

本文利用基于浸入边界法的IB2d软件包，通过修改相应的代码程序来建立仿真模型、设置边界约束和仿真参数等。

1)柔性壁面仿真模型

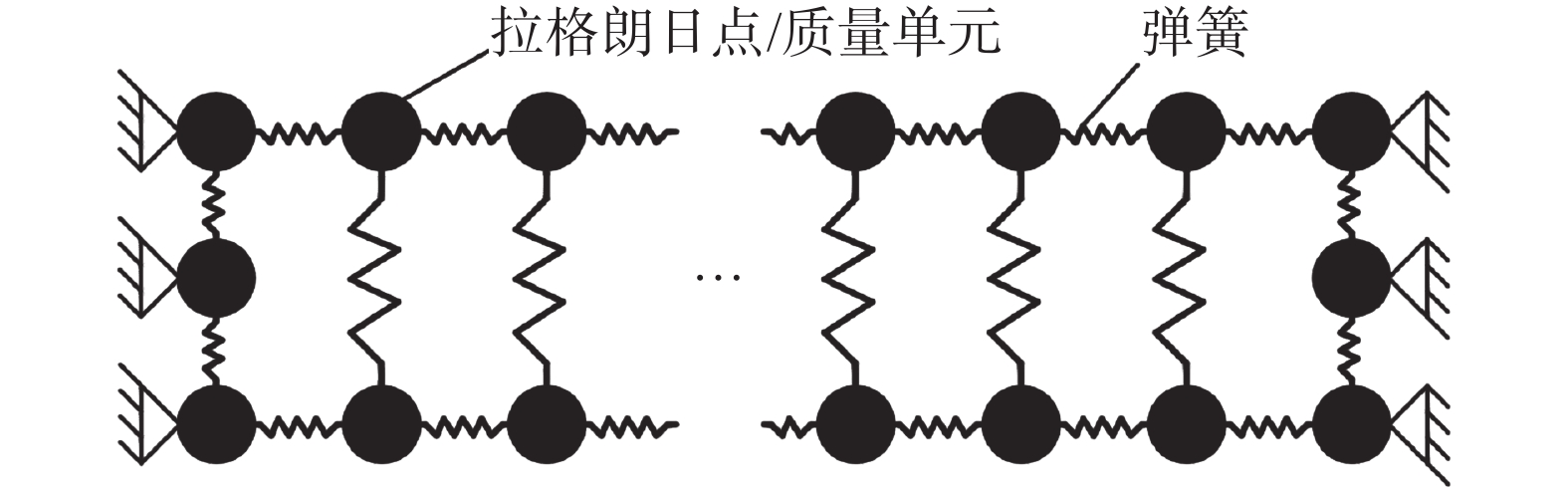
柔性蒙皮外层柔性壁面的材料为聚氨酯弹性体的柔韧薄膜，其尺寸为 $1\;{\rm{ m}} \times 1\;{\rm{ m}} \times 4\;{\rm{ mm}}$ ，使用建模单元中的拉格朗日点、弹簧和质量单元建立柔性壁面仿真模型，如图2所示。

由图2可知，柔性壁面的浸入边界由若干拉格朗日点组成，其上、下两面为浸入边界，左、右两侧面为边界约束。模型中每2个相邻点的距离为2 mm，柔性壁面x方向长为1 m，沿x方向的上、下2个浸入边界各由501个拉格朗日点组成；默认z方向为单位长度；y方向厚4 mm，左右两侧设置3个拉格朗日点作为固定约束，在每个拉格朗日点上附加相同质量单元，模拟柔性壁面本身的质量。每2个相邻拉格朗日点之间连接弹簧单元，模拟柔性壁面x和y方向上的刚度。

2)弹性支撑仿真模型

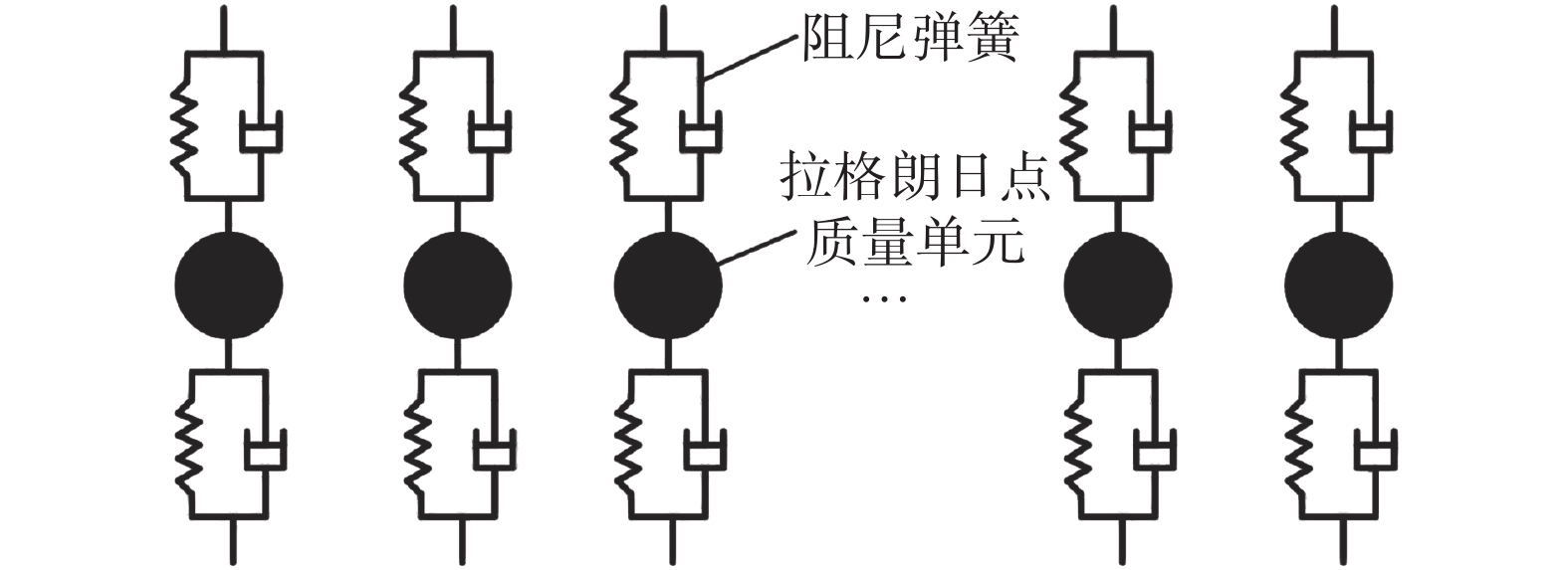
柔性蒙皮内层的弹性支撑是分布式双层隔振系统。使用建模单元中的拉格朗日点、阻尼弹簧和质量单元建立弹性支撑，如图3所示。

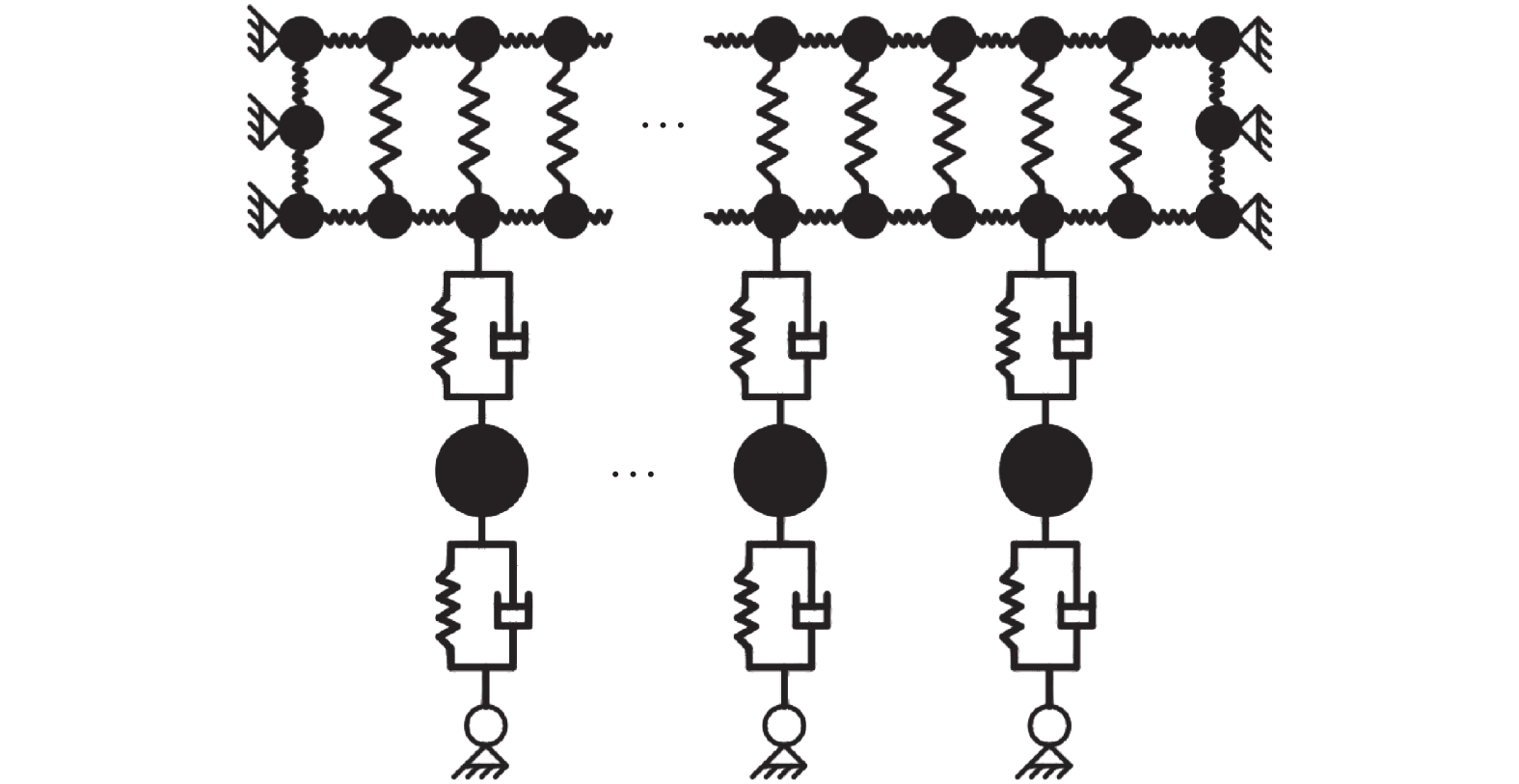
根据上述建模过程，建立的双层柔性蒙皮仿真模型如图4所示。

2 算例验证 2.1 圆柱绕流

圆柱绕流是流体力学中的经典问题，对其有许多的理论以及实验研究^[10-12]，方便对仿真结果进行验证。因此，本文按照文献[10-12]中的圆柱绕流试验参数进行了圆柱绕流仿真计算，在仿真与试验参数一致的情况下，验证了IB2d数值计算结果的准确性。

设置计算域尺寸为1 m×0.25 m，选择直径为D=0.08 m的圆柱，以计算域左下角为原点，圆柱中心位于(0.1 m，0.125 m)。流体密度 $\;\rho $ 设定为100 kg/m³，流场速度v=1 m/s。取网格为512×128，时间步长为5×10⁻⁵ s。确定上述的参数后，设定计算时间为27 s，即无量纲时间T=180，测量涡脱落时间并计算涡脱落频率，最后求得斯特劳哈尔数、阻力系数、升力系数。按上述的参数设置并完成仿真计算，得到雷诺数分别为100、150和200时的斯特劳哈尔数，并与其他研究人员实验测量数据^[10-12]进行对比，如表1所示。由表可知，基于浸入边界法数值计算得到的斯特劳哈尔数与实验测量数据具有很好的一致性。

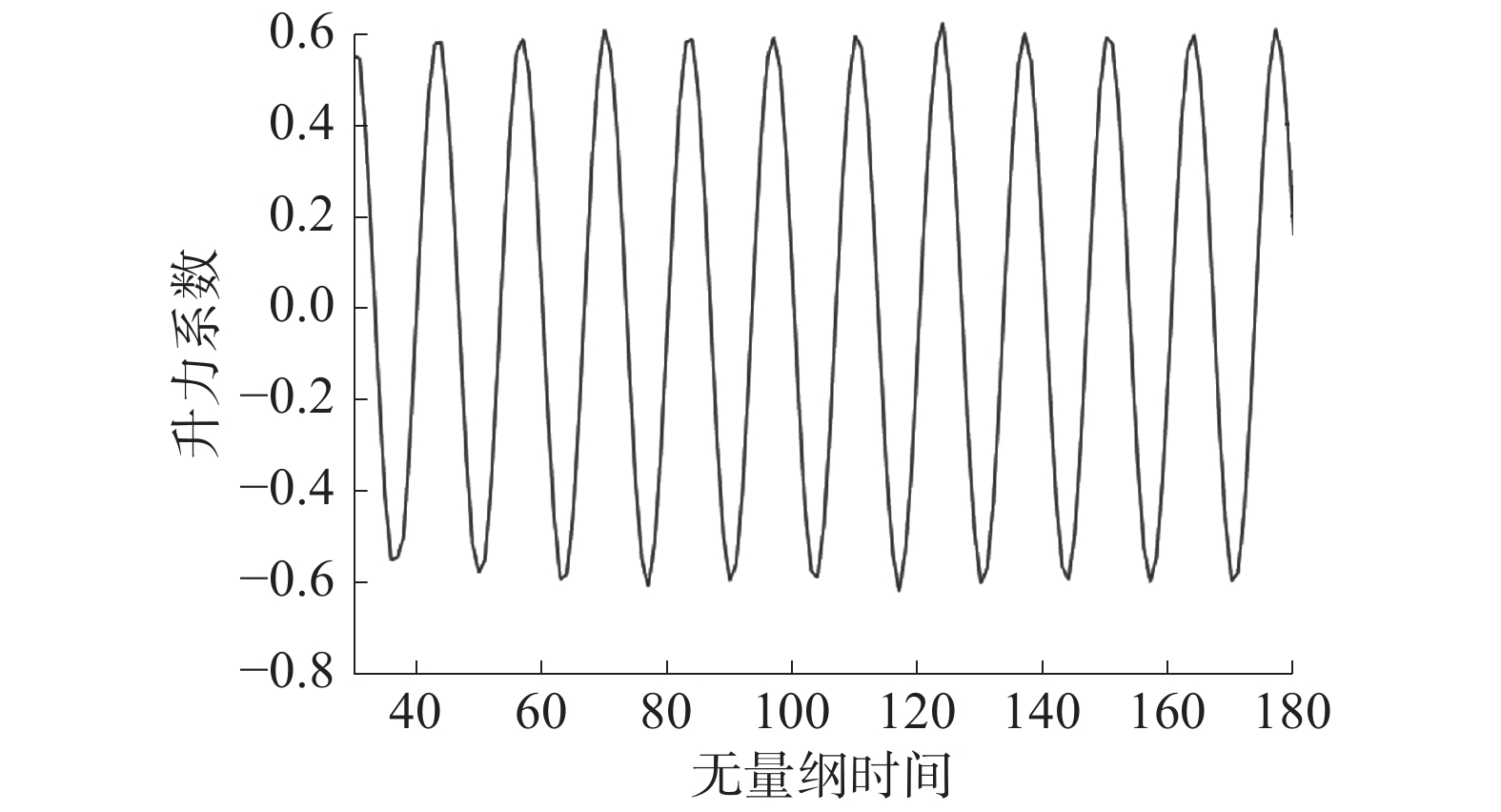
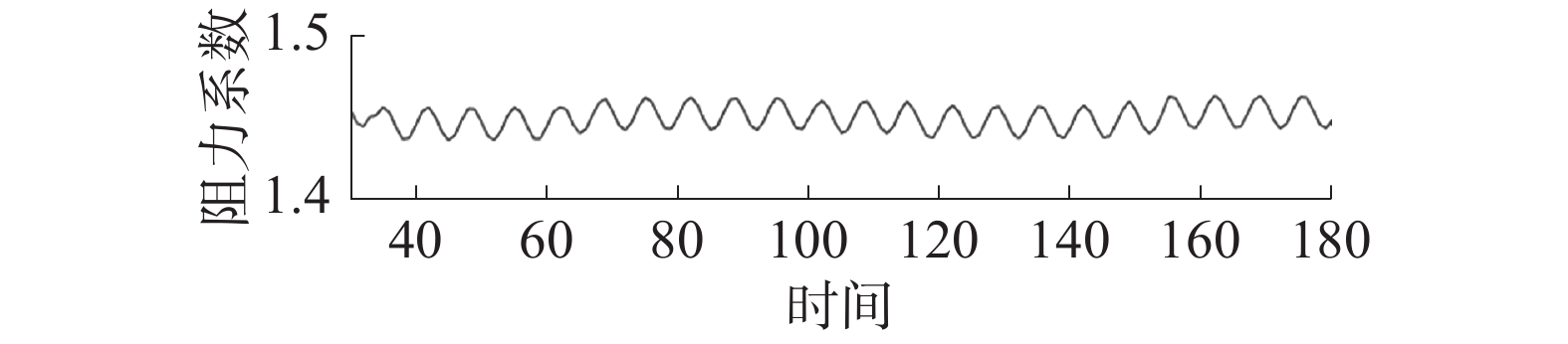
Re=150时圆柱绕流的升力系数和阻力系数曲线分别如图5和图 6所示。

将本文得到的平均升力和阻力系数与Lai等^[10]的结果进行对比，结果如表2所示。由表可知，本文计算结果与其计算结果吻合良好。

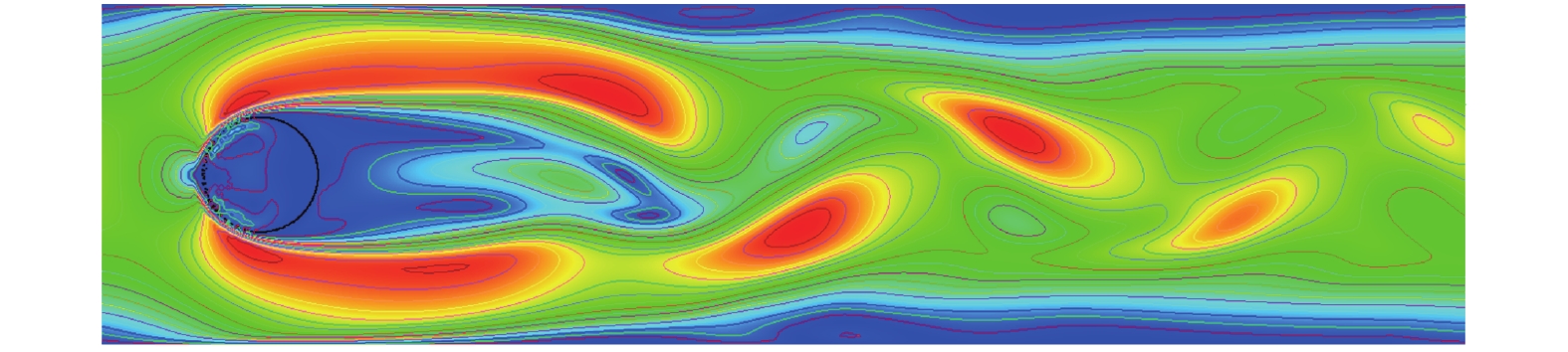
本文在Re=150、计算时间T=180时，根据数值计算结果绘制涡脱落的瞬时涡度等值线，得到圆柱尾涡状态如图7所示。由图可知，沿圆柱表面分布的边界层、分离剪切层的卷起以及圆柱后侧的分离区域都清晰可见。圆柱尾涡出现明显正、负交替向下游发展的卡门涡街现象。

综上，根据圆柱绕流算例中的升力系数、阻力系数、斯特劳哈尔数以及圆柱绕流尾涡状态，验证了IB2d数值计算结果的准确性。

2.2 柔性丝线

为进一步说明IB2d软件包解决柔性大变形流固耦合问题的准确性和有效性，本文利用柔性丝线案例对其进行了验证。

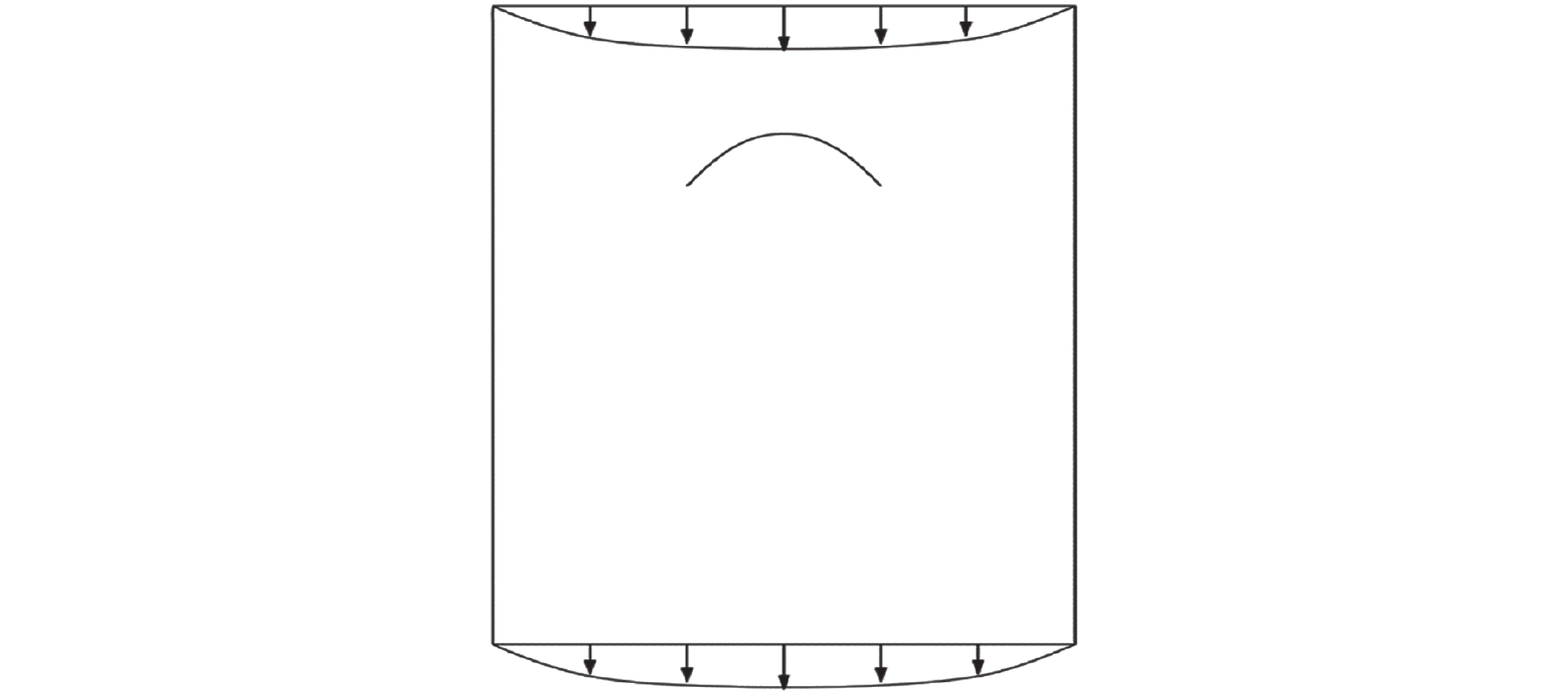
本算例来源于Zhu^[13]的数值仿真。考虑一种不可压缩黏性流体在重力驱动下的二维垂直流动，弹性纤维最初水平放置在实验通道中心，中点固定在顶部边界附近。通道的2个侧壁是刚性的，侧壁上的速度采用无滑移边界条件。其计算模型示意图如图8所示。仿真参数设置如表3所示。

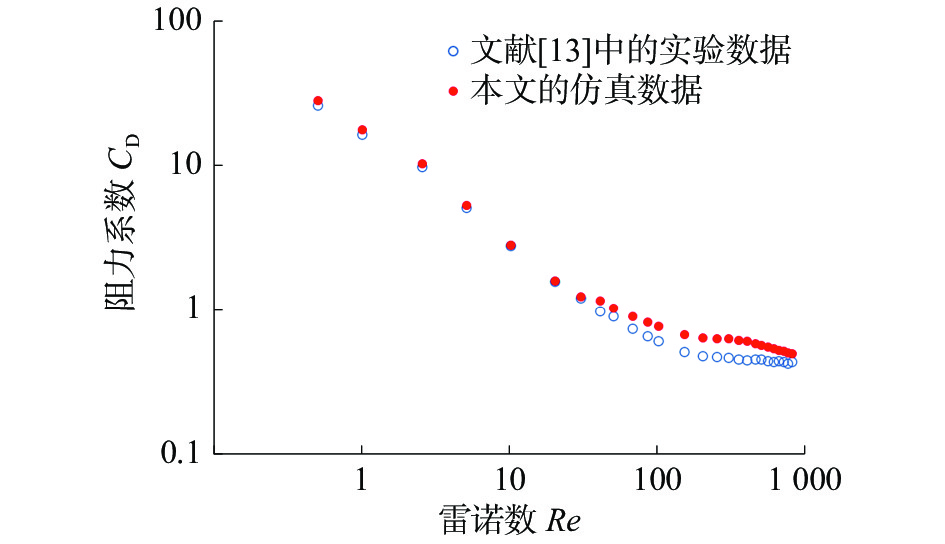
按照表3的参数进行仿真计算，所得到的计算结果如图9所示。由图可知，仿真结果与文献[13]中的实验结果相吻合，进一步说明了IB2d软件包能够处理大变形问题，且具有较好的精度。

3 双层柔性蒙皮仿真结果分析 3.1 仿真参数设置

仿真模型边界约束为柔性壁面左、右两侧面以及各弹性支撑底端，边界约束的虚拟弹簧刚度取2×10⁹ N/m。在流体域尺寸为1.6 m×0.6 m，网格密度为400×150时，满足了刚性边界条件。同理，质量单元虚拟弹簧刚度也设置为2×10⁹ N/m。流体密度 $\rho $ 设置为100 kg/m³，动力黏度为0.001 N·s/m²，背景流速u分别设置为2、5、10、20 m/s，则蒙皮中点处的雷诺数分别为1×10⁵、2.5×10⁵、5×10⁵、1×10⁶。

3.2 仿真参数可行性验证

为了验证本文中的网格密度的可行性，取时间步长为5×10⁻⁵ s，流速为5 m/s，网格密度分别取400×150、400×300、800×300以及800×600时进行仿真计算，并以网格密度为800×600时对应的平均阻力系数为基准，计算了另外3种网格密度相对于800×600时平均阻力系数的误差，结果如表4所示。

由表4可知，网格密度为800×600时的平均阻力系数相对于800×300时不发生变化，并且平均阻力系数在网格密度为400×150时相对于网格密度为800×600时的误差仅为1.8%，满足仿真计算要求。为了提高计算效率，选择400×150的网格密度。

为了验证本文中时间步长的取值合理，在网格密度为400×150的情况下，取流速为5 m/s，时间步长分别取5×10⁻⁵、2.5×10⁻⁵、1×10⁻⁵ s进行仿真计算，并以1×10⁻⁵ s对应的平均阻力系数为基准，计算了另外2种时间步长相对于1×10⁻⁵ s时平均阻力系数的误差，结果如表5所示。

由表5可知，随着时间步长的增加，误差不发生变化，并且随着时间步长的增加平均阻力系数相差较小，即3种时间步长都满足仿真计算要求。为提高计算效率，本文选择时间步长为5×10⁻⁵ s对双层柔性蒙皮进行仿真计算。

3.3 不同参数下双层柔性蒙皮减阻性能分析

本文以阻力系数衡量双层柔性蒙皮的减阻性能。柔性蒙皮在流体作用下所受的阻力来自2个方面，即剪切应力和分布在柔性蒙皮浸入边界上的压力。根据蒙皮浸入边界对流体网格施加的力的x分量，即仿真结果中x方向的欧拉力f₁，计算柔性蒙皮的阻力。柔性蒙皮阻力F_R的计算公式为

$ {F_{\rm{R}}} = - \int_{\varOmega} {{f_1}{\rm{d}}x = - \sum\limits_x {{f_1}(x){h^2}} } $

式中 $h$ 为欧拉网格宽度。

$ {C_{\rm{R}}} = \frac{{{F_{\rm{R}}}}}{{\rho {u^2}L}} $

通过以下物理量包括来流速度 $U_\infty ^*$ ，流体密度 $\;{\rho ^*}$ ，柔性壁厚度 $b_{}^*$ ，柔性壁质量 $m_1^*$ ，中间质量 $m_2^*$ ，上、下层弹簧刚度 $k_1^*$ 、 $k_2^*$ ，支撑间距 ${l^*}$ (上标*代表有量纲值)，可以得到柔性壁质量 ${m_1}$ ，中间质量 $m_2^{}$ ，上、下层弹簧刚度 $k_1^{}$ 、 $k_2^{}$ ，支撑间距 $l$ 的无量纲化表达式分别为

$ \begin{array}{l} {m_1} = \dfrac{{m_1^*}}{{{\rho ^*}{b^*}}} \\ {m_2} = \dfrac{{m_2^*}}{{{\rho ^*}{b^*}}} \\ {k_1} = \dfrac{{k_{^1}^*{b^*}}}{{{\rho ^*}U_\infty ^{{*^2}}}} \\ {k_2} = \dfrac{{k_2^*{b^*}}}{{{\rho ^*}U_\infty ^{{*^2}}}} \\ l = \dfrac{{{l^*}}}{{{b^*}}} \end{array} $

3.3.1 弹性支撑间距对蒙皮减阻性能的影响

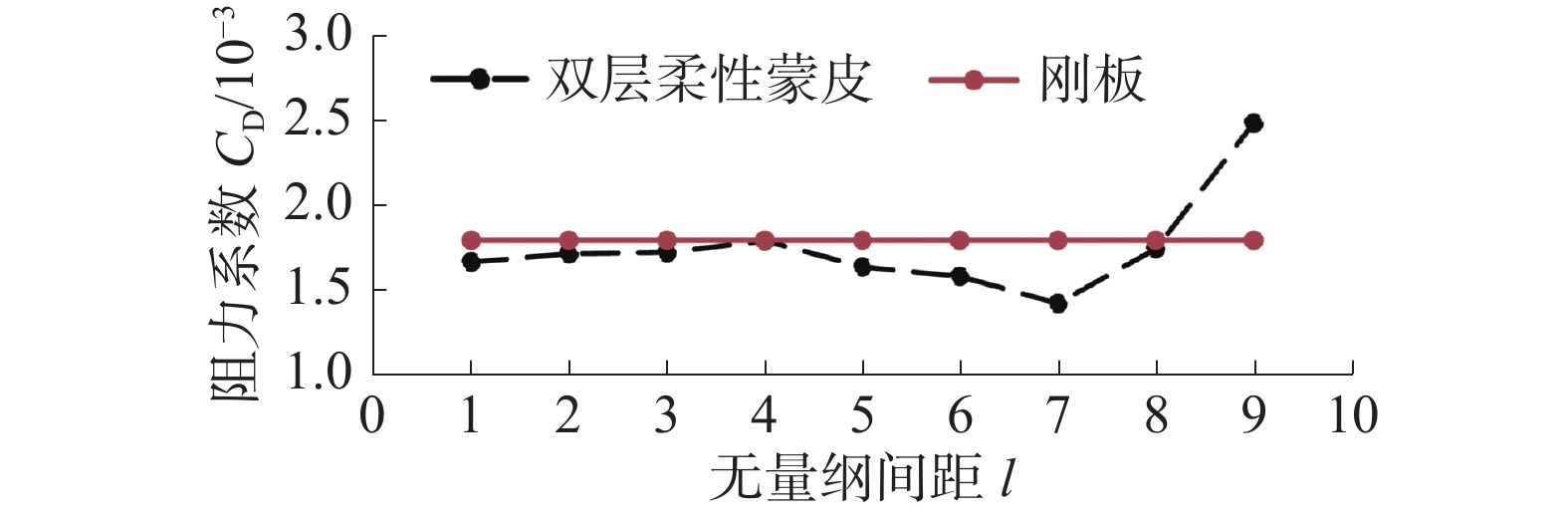
设置蒙皮无量纲结构参数为：m₁=0.4、m₂=0.4、k₁=0.4、k₂=0.4，对双层柔性蒙皮模型进行了数值计算，得到不同间距l下蒙皮的阻力系数C_D如图10所示。同时，为更加直观地反映蒙皮的减阻效果，在相同流场环境下对刚性平板的阻力系数进行了数值计算。由图可知，l=1~4时，双层柔性蒙皮的阻力系数C_D随间距l的增大而增大，且l=7时的阻力系数最小，l=9时的阻力系数最大。值得注意的是，l=1~8时，双层柔性蒙皮的阻力系数C_D均小于刚性平板，表明蒙皮在此间距范围内具备减阻效果。

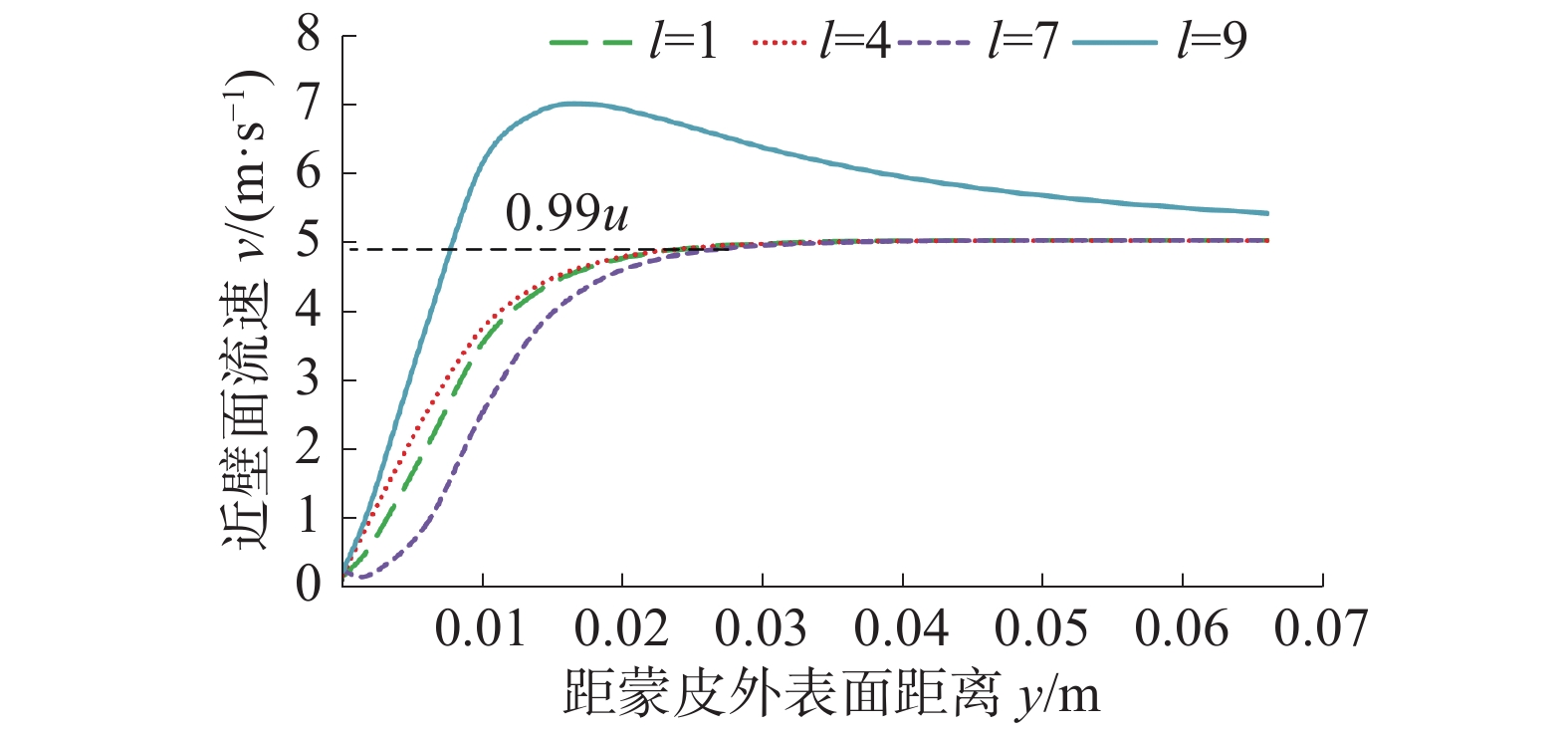
为探究间距l对阻力系数C_D的影响机理，给出双层柔性蒙皮近壁面速度分布曲线如图11所示。由图可知，l=4时的近壁面流速比l=1时的要大，且l=7时近壁面流速最小，l=9时近壁面流速最大。而近壁面流速降低会使黏性阻力减小，进而印证了图10所示的蒙皮阻力系数C_D随间距l变化的规律。

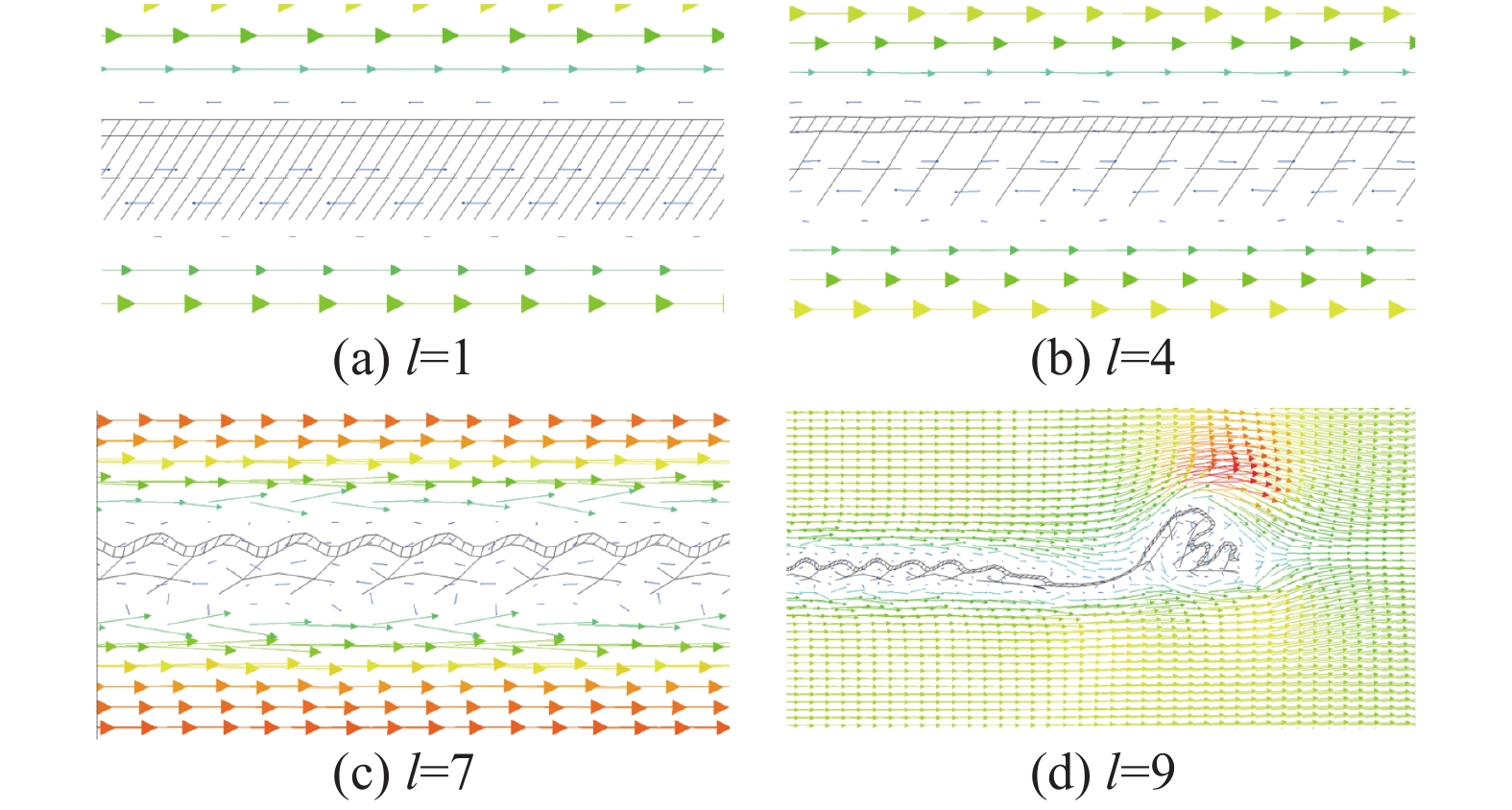
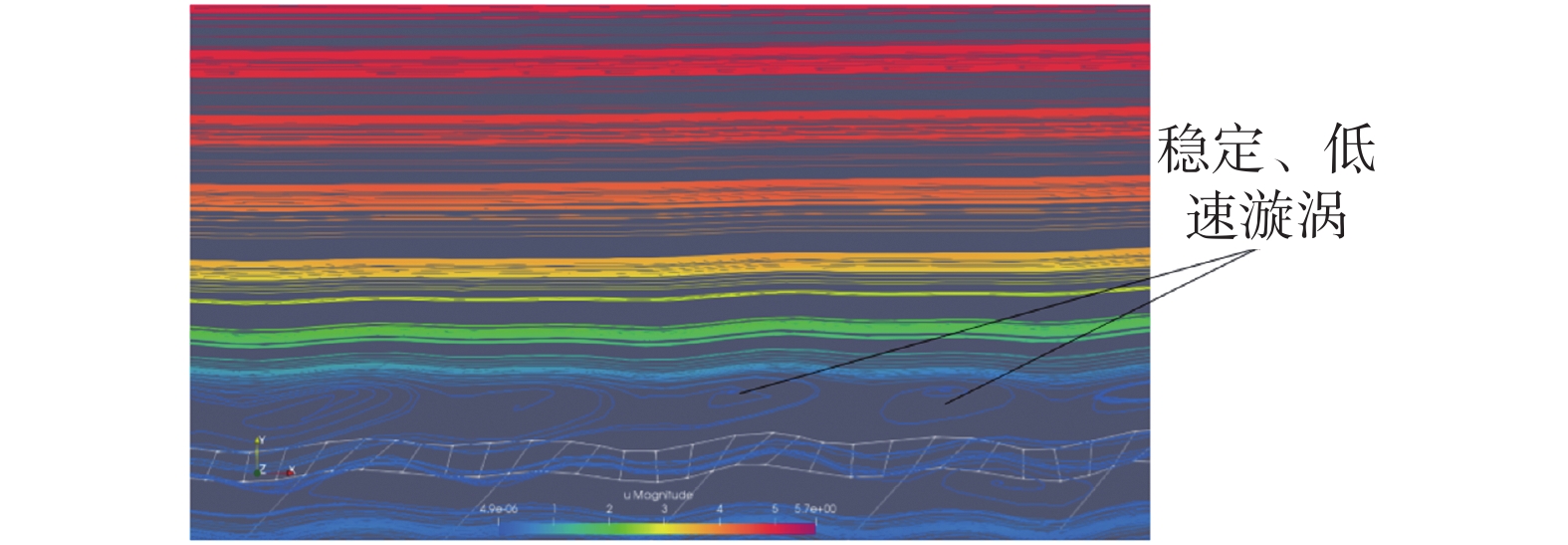
下面从结构变形的角度探究蒙皮阻力系数C_D随间距l变化的规律。给出双层柔性蒙皮表面流速矢量图以及速度流线如图12和图13所示。由图12可知，l=1、4时，双层柔性蒙皮几乎不产生明显的变形。l=7时，双层柔性蒙皮发生类似于波浪型的变形，且在其下凹处存在着稳定、低速的漩涡(图13)。根据胡海豹等^[14]的研究结果表明，稳定、低速的漩涡可以起到类似于滚动轴承的作用，将流体之间的滑动摩擦转变为滚动摩擦，从而减小了蒙皮受到的摩擦阻力。l=9时，由于支撑间距较大，双层柔性蒙皮结构在流体的作用下被破坏，因而使其阻力系数急剧增大。

3.3.2 弹性支撑刚度比对蒙皮减阻性能的影响

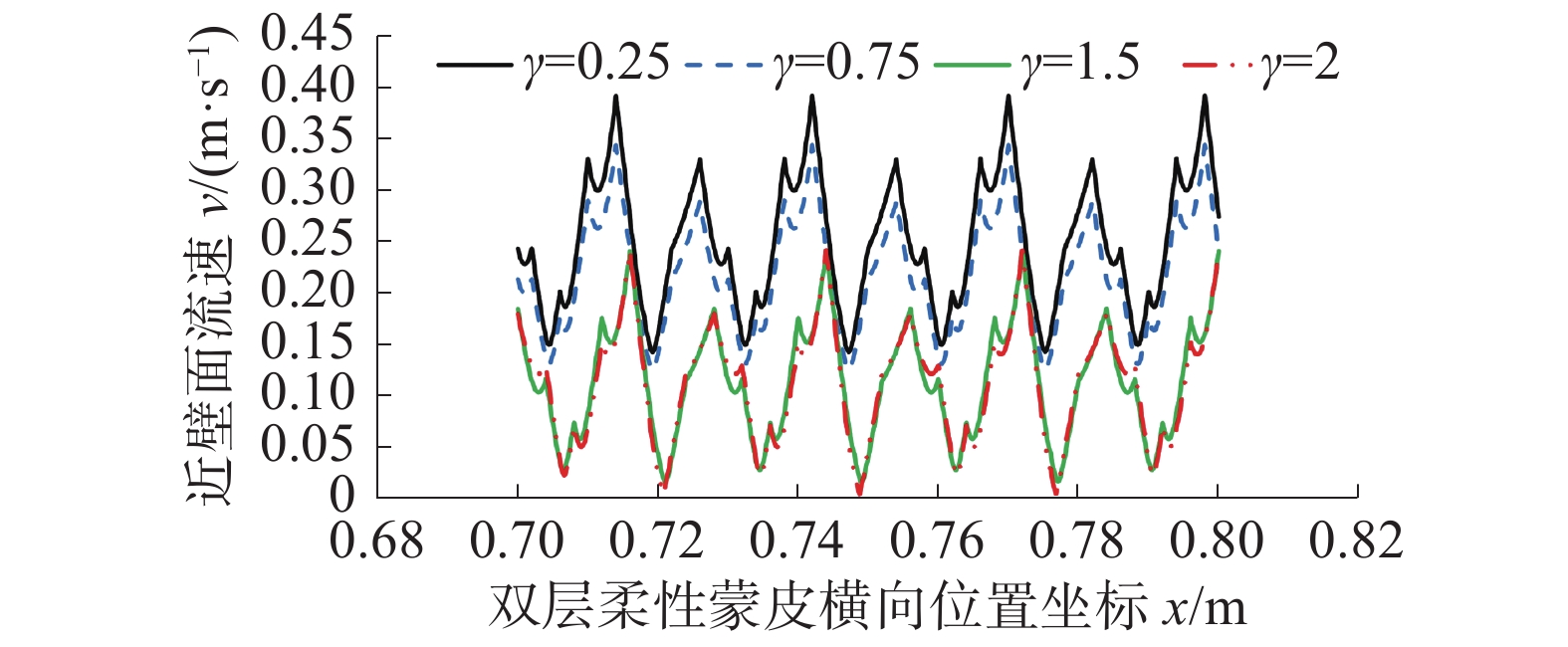
设置蒙皮无量纲结构参数为l=7、m₁=0.4、m₂=0.4、k₂=0.4，对双层柔性蒙皮模型进行了数值计算。得到不同刚度比γ下蒙皮的阻力系数C_D如图14所示。由图可知，γ=0.25~1.5时，阻力系数C_D随着刚度比γ的增大逐渐减小，而继续增大刚度比γ=2时，双层柔性蒙皮的阻力系数几乎未发生变化。为探究刚度比γ对阻力系数C_D影响的内在机理，给出图15所示的双层柔性蒙皮近壁面流速图。由图可知，γ=0.25~1.5时，双层柔性蒙皮近壁面流速随刚度比的增大而减小；而继续增大刚度比γ=2时，蒙皮近壁面流速几乎不变。这与图14所示的蒙皮阻力系数C_D随刚度比γ的变化规律一致。进而说明了在一定范围内增大刚度比可以减小蒙皮近壁面流速，从而使阻力系数减小。

3.3.3 流速对蒙皮减阻性能的影响

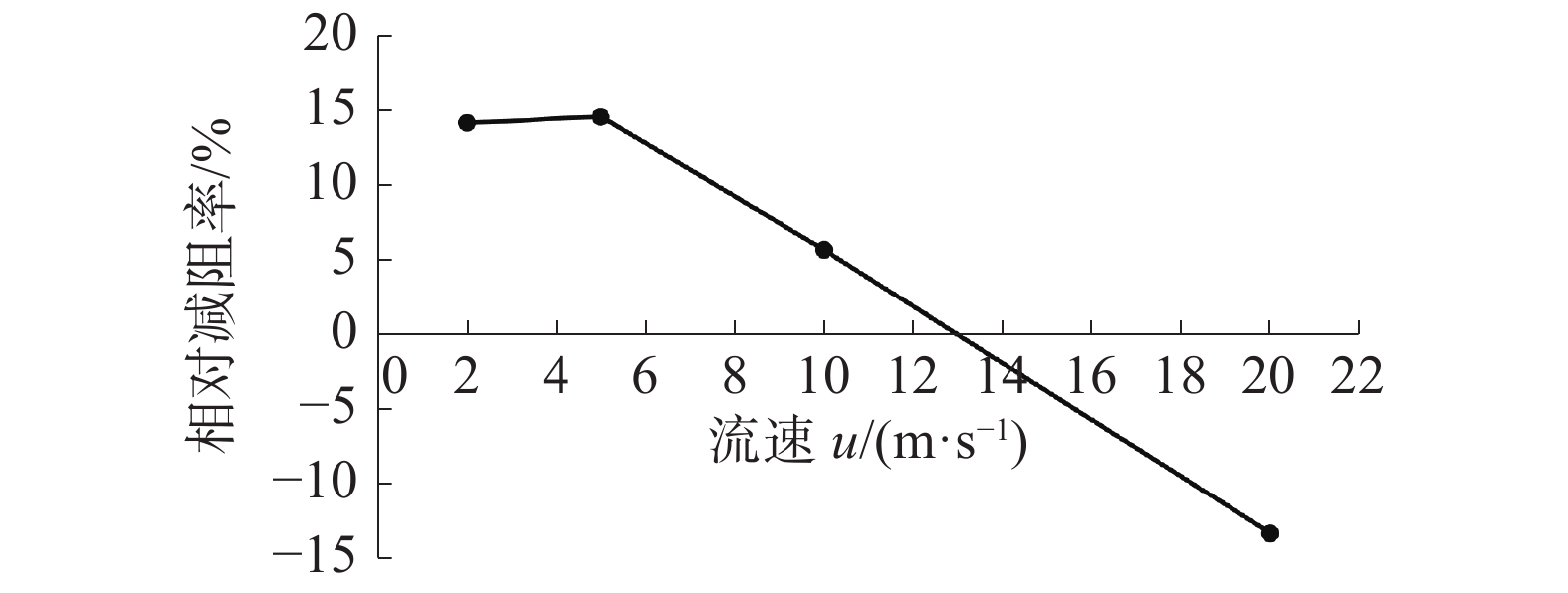
设置蒙皮无量纲结构参数为l=7、m₁=0.4、m₂=0.4、k₁=0.4，k₂=0.4，分别在流速为2、5、10、20 m/s情况下，对双层柔性蒙皮进行建模以及仿真计算。得到相对减阻率η随流速u的变化情况如图16所示。由图可知，u=2、5 m/s时，蒙皮的相对减阻率随流速的增大而增大，且最大相对减阻率可达14.48%。当流速u增大到10 m/s时，蒙皮的相对减阻率降低至5.61%，而继续增大流速u至20 m/s时，相对减阻率为−13.36%，表明蒙皮在此流速下不具备减阻性能。

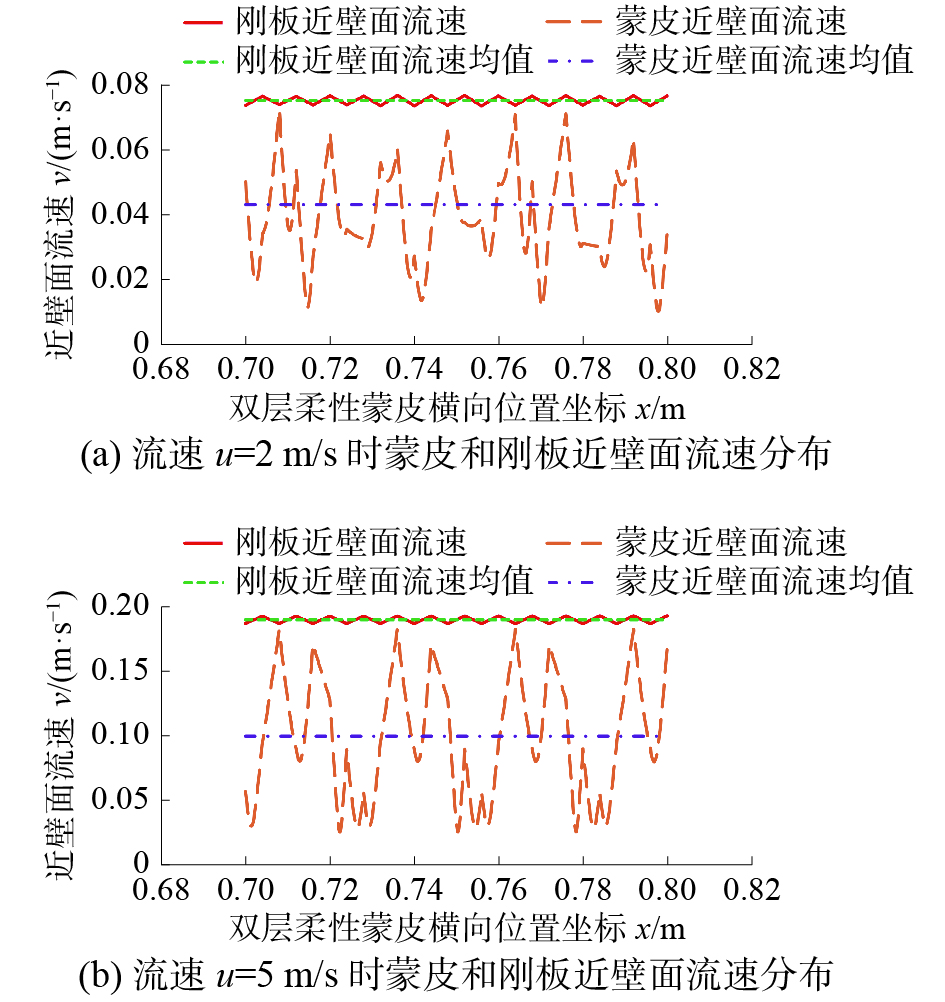
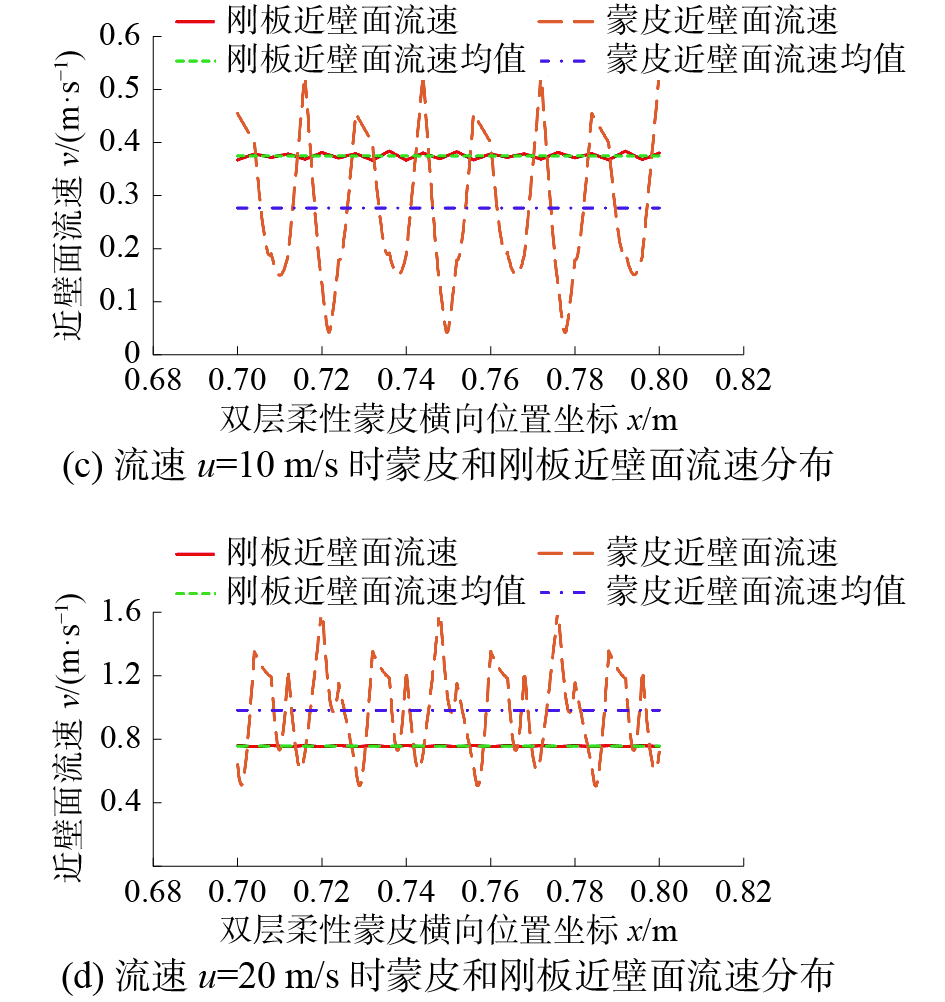
为探究流速对蒙皮相对减阻率影响的内在机理，给出不同流速下的近壁面流速曲线如图17所示。由图可知，u为2、5 m/s时，双层柔性蒙皮近壁面流速均值小于刚板近壁面流速均值，表明双层柔性蒙皮在此流速下具备减阻效果，且蒙皮近壁面平均流速减小率随外加流场流速的增大而增大；外加流场流速增大至u=10 m/s时，平均流速减小率降低；而增大外加流场流速至u=20 m/s时，刚板近壁面流速均值小于双层柔性蒙皮流速均值，说明此时双层柔性蒙皮不具备减阻效果。这与图16所示的相对减阻率随流速的变化规律一致。进而说明了在一定范围内增大流速会使双层柔性蒙皮的减阻性能先提高后降低。

4 结论

本文从水下航行器流体减阻的设计需求出发，将双层隔振系统微小化、阵列化，结合柔性壁面减阻技术构建出了一种双层柔性蒙皮结构，并基于浸入边界法对其减阻性能进行了仿真计算，结论如下：

1）间距l=1~8时，双层柔性蒙皮的阻力系数小于刚板的阻力系数，表明双层柔性蒙皮结构在特定的间距下具备减阻效果。

2）在一定范围内增大刚度比会使近壁面流速降低，从而起到减小黏性阻力、提高蒙皮减阻性能的作用。

3）特定结构参数的双层柔性蒙皮在13 m/s的流速范围内具备减阻效果，对于更高流速下的减阻性能还有待对其结构参数优化后进一步的探究。