盲源分离问题最早起源于“鸡尾酒会”，目的是在源信号与混合矩阵均未知的情况下，从观测到的若干个混合信号中分离出有用的信号^[1]。盲源分离技术经过多年的发展，已经在众多领域得到了广泛的应用。近些年随着图像处理和神经网络等学科领域的不断兴起，盲源分离技术又具有了新的研究价值和实用意义^[2-3]。当观测信号数量小于源信号时，这一问题可具体为欠定盲源分离问题，欠定盲源分离在工程运用中更具实用价值，但同时技术难度更大，因此欠定盲源分离问题在未来有待进一步的发展。目前解决欠定盲源分离的主流方法是稀疏分量分析法，这一方法要求先对混合矩阵进行估计，再进一步恢复出源信号，因此估计出一个高精度的混合矩阵对最终的恢复效果至关重要，直接影响最终的重构效果^[4-5]。近些年来，随着对各种聚类算法的研究，FCM算法成为解决混合矩阵估计的主流算法之一。FCM算法相比K-means、K-Hough等算法^[6-7]有数据划分详细、归类精准的优点，但这一算法也存在诸多缺陷。FCM算法需要预先设定聚类数目，且存在对初始聚类中心敏感的问题，初始聚类中心的设置不当有时会对聚类产生灾难性的后果^[8]。此外，噪点的存在也会使聚类中心发生偏移，影响最终的聚类结果。本文针对这些问题提出了基于密度结构分析的改进FCM算法，并以此为基础实现混合矩阵估计。

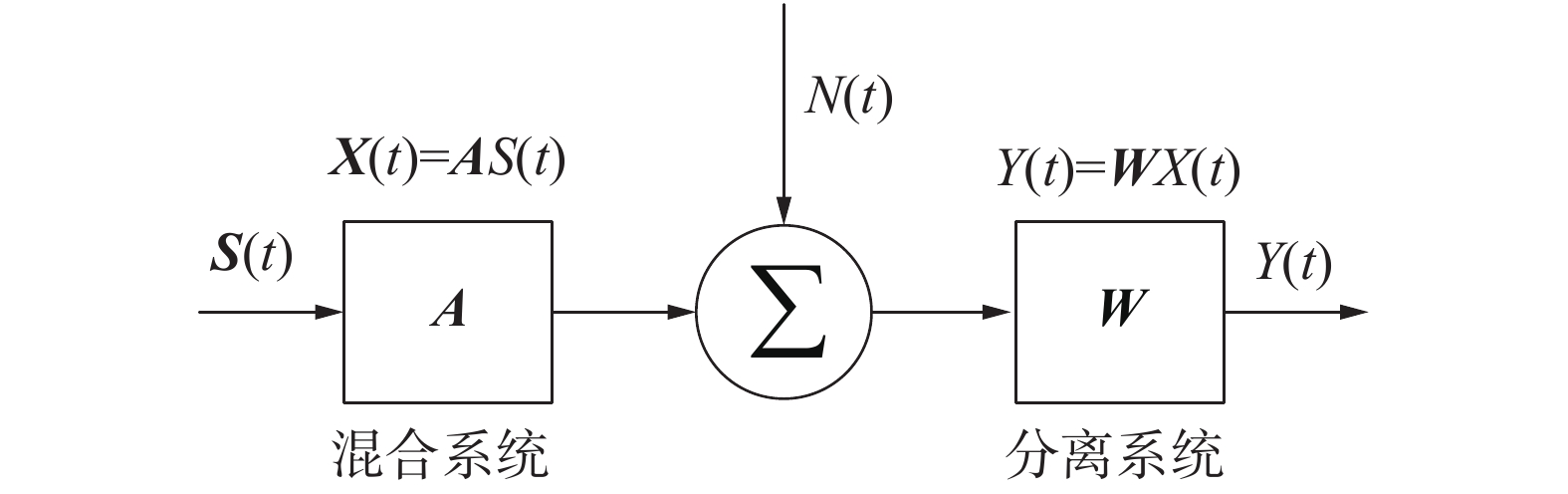
1 盲源分离问题 1.1 盲源分离模型

通用的盲源分离模型如图1所示。

盲源分离模型主要分为混合系统和分离系统2部分。混合系统的数学模型可表示为

${{X}}(t) = {{A}}{{S}}(t) + N(t){\text{}}$

(1)

式中： $X(t) = \left[ {{x_1}(t),{x_2}(t), \cdots ,{x_M}(t)} \right]$ 为在t时刻接收到的M维观测信号；混合矩阵 ${{A}}$ 为 $M \times N$ 维矩阵； ${{S}}(t) = \left[ {{s_1}(t),{s_2}(t), \cdots ,{s_M}(t)} \right]$ 为维度为 $N$ 的源信号； $N(t)$ 为传输过程中的噪声信号。

分离模型对应的数学公式为

${{Y}}(t) = {{W}}X(t){\text{}}$

(2)

式中： ${{Y}}(t) = \left[ {{y_1}(t),{y_2}(t), \cdots ,{y_N}(t)} \right]$ 为分离之后最终估计出来的源信号；W为分离矩阵。一般来说，当分离矩阵 ${{W}} = {{{A}}^{ - 1}}$ 估计出来的源信号精度最高。

实际应用中，根据盲源分离源信号数目n和观测信号数目m的不同，可分为不同的情况：当m ${\rm{ = }}n$ 时，属于正定盲源分离；当m ${\rm{}} > n$ 时，属于超定盲源分离；当m ${\rm{ < }}n$ 时，属于欠定盲源分离。文章主要研究欠定盲源分离情况。

1.2 预处理

在欠定盲源分离问题中，由于直接接收到的混合信号方向聚集性很差，并且存在大量冗余，进行预处理可以一定程度上增强信号的线性聚集性，去除绝大多数的冗余散点，提高计算效率。

预处理首先需要对接收到的混合信号做短时傅立叶变换。在时域范围内，信号的方向聚集性很差，在完成短时傅立叶变换之后，从时频域的角度处理，信号的方向聚集性能够得到一定的增强。

在时频变换的基础上需要进一步去除低能量点。由于线性盲源分离混合矩阵的散点图对应多条直线，一般情况下，离原点中心较远的散点对直线的方向确定影响较大，而一些距离原点中心距离较近的低能量点作用不大，反而由于其离散性会对估计结果造成干扰。因此，有必要筛选掉这些低能量时频点，低能量点的判定公式如下

$\left\| {x(t,k)} \right\| > \sigma \cdot \max \left\| {x(t,k)} \right\|\;\;{\kern 1pt} (t,k) \in \Omega $

(3)

公式(3)中参数 $\sigma \in (0,1)$ ，通常情况下取值范围为0.05~0.2，具体的数值根据实际情况选取。在去除绝大多数的低能量点后，观测信号时频点的集合变小，留下的散点对混合矩阵的估计更具有实际意义。

1.3 单源等比处理

欠定盲源分离情况下，接收到的混合信号在实际应用过程大多都不是天然稀疏的，但是通过选取适当的稀疏基，仍可以将信号进行稀疏表示^[9-10]。对稀疏性较差的信号，为增强信号在特定稀疏基下的稀疏表示能力，可以对混合信号做单源等比处理。由于不同的源信号在时域上无法完全同步，因此必然存在某些时刻只有一个信号起主要作用，而其他信号为零或无限趋近于零，这种时刻点存在的时频点称为单源时频点。经过公式推导，在这种情况下理论上各观测信号时频点实部与虚部之间比值为一恒定值，等于混合矩阵对应列向量的比值，这一比值称为单源等比系数。单源等比模型可用以下公式表示

$\frac{{{\rm{Re}} \left\{ {{x_i}\left( {{t_1},{k_1}} \right)} \right\}}}{{{\rm{Re}} \left\{ {{x_j}\left( {{t_1},{k_1}} \right)} \right\}}} = \frac{{{\rm{Im}} \left\{ {{x_i}\left( {{t_1},{k_1}} \right)} \right\}}}{{{\rm{Im}} \left\{ {{x_j}\left( {{t_1},{k_1}} \right)} \right\}}} = \frac{{{a_{i1}}}}{{{a_{j1}}}}{\text{}}$

(4)

在实际问题中，各个信号分量实部或虚部之间的比值不可能完全相等，这里定义一个常数 $\omega $ 为误差阈值。这样最终的单源等比模型可修正为

$\left| {\dfrac{{\dfrac{{{\rm{Re}} \left\{ {{x_i}\left( {{t_1},{k_1}} \right)} \right\}}}{{{\rm{Re}} \left\{ {{x_j}\left( {{t_1},{k_1}} \right)} \right\}}} - \dfrac{{{\rm{Im}} \left\{ {{x_i}\left( {{t_1},{k_1}} \right)} \right\}}}{{{\rm{Im}} \left\{ {{x_j}\left( {{t_1},{k_1}} \right)} \right\}}}}}{{\dfrac{{{\rm{Re}} \left\{ {{x_i}\left( {{t_1},{k_1}} \right)} \right\}}}{{{\rm{Re}} \left\{ {{x_j}\left( {{t_1},{k_1}} \right)} \right\}}} + \dfrac{{{\rm{Im}} \left\{ {{x_i}\left( {{t_1},{k_1}} \right)} \right\}}}{{{\rm{Im}} \left\{ {{x_j}\left( {{t_1},{k_1}} \right)} \right\}}}}}} \right| < \omega {\text{}}$

(5)

式中 $\omega $ 的经验值为(0,1)。

2 基于改进FCM算法的混合矩阵估计 2.1 FCM聚类算法

FCM算法是一种基于隶属度划分的模糊聚类算法，该算法可具体描述为：假设样本集合为 $X = \left\{ {{x_1},{x_2}, \cdots ,{x_n}} \right\}$ ，聚类中心为 $C = \left\{ {{c_1},{c_2}, \cdots ,{c_n}} \right\}$ ，将它分为c类，引入隶属度矩阵 ${{U}}\left( x \right)$ ，使得下面给定的目标函数式(6)趋于最小

$J({{U}},C) = \sum\limits_{i = 1}^c {\sum\limits_{j = 1}^n {u_{ij}^m} } {\left\| {{x_j} - {c_i}} \right\|^2},1 \leqslant m < \infty {\text{}}$

(6)

其中隶属度满足归一化约束条件

$\sum\limits_{i = 1}^c {{u_{ij}}} = 1,{u_{ij}} \geqslant 0{\text{}}$

(7)

FCM算法具体计算如下。

1) 初始化所有参数，包括阈值 $\varepsilon $ ，聚类中心 ${C_0}$ ，模糊系数 $m$ ，迭代次数 $l = 0$ ，最大迭代次数 $T$ 以及隶属矩阵 ${{{U}}_0}$ 。

2) 利用式(8)和式(9)更新聚类中心 $C$ 和隶属度矩阵U。

${c_i} = \dfrac{{\displaystyle\sum\limits_{j = 1}^n {u_{ij}^m} {x_j}}}{{\displaystyle\sum\limits_{j = 1}^n {u_{ij}^m} }}{\text{}}$

(8)

${u_{ij}} = \dfrac{1}{{\displaystyle\sum\limits_{k = 1}^c {{{\left[ {\dfrac{{{d_{ij}}}}{{{d_{kj}}}}} \right]}^{\frac{2}{{m - 1}}}}} }}{\text{}}$

(9)

式(9)中， ${d_{ij}} = \left\| {{x_j} - {c_i}} \right\|$ ， ${d_{kj}} = \left\| {{x_j} - {c_k}} \right\|$ 。

3) 计算相邻两次目标函数之差，若差值小于阈值 $\varepsilon $ ，或达到最大迭代次数 $T$ ，结束算法，输出隶属矩阵U和聚类中心 $C$ 。否则返回步骤2)，继续迭代，直到满足要求。

2.2 基于OPTICS算法的密度结构分析

OPTICS聚类算法是基于密度的聚类算法，目标是将空间中的数据按照密度分布进行聚类，理论上可以获得任意密度的聚类^[11-12]。OPTICS算法在DBSCAN基础上新增了核心距离和可达距离的概念。

核心距离：当某一数据点 $p \in D$ ，D为数据集合，以该点为核心，包含 $\min P$ 个数据点的最小邻域半径定义为核心距离，表达式为

$cd(p) = \left\{ {\begin{array}{*{20}{l}} {{\rm{undefined,}}}&{\left| {{N_\varepsilon }(p)} \right| < {\rm{min}}P} \\ {d\left( {p,N_\varepsilon ^{\min P}(p)} \right)},&{\left| {{N_\varepsilon }(p)} \right| \geqslant {\rm{min}}P} \end{array}} \right.$

(10)

式中 $N_\varepsilon ^i\left( x \right)$ 为集合中所有与 $p$ 邻近的散点。

可达距离：假定 $p,o \in D$ ，对于给定的 $\varepsilon $ 和可 $\min P$ ，可达距离可定义为

$L(o,p) = \left\{ {\begin{array}{*{20}{l}} {{\rm{undefined,}}}&{\left| {{N_\varepsilon }(p)} \right| < {\rm{min}}P} \\ {\max \{ cd(p),d(o,p)\} },&{\left| {{N_\varepsilon }(p)} \right| \geqslant {\rm{min}}P} \end{array}} \right.$

(11)

可达距离可以理解为在 $p$ 是核心点、并且 $p$ 与 $o$ 密度可达的条件下，核心点对应的最小邻域半径。

OPTICS算法总结如下。

算法输入：数据集合 $D$ ， $\varepsilon $ 和 $\min P$ 。

算法输出：可达序列和相应的可达序列图。

预处理：初始化各种参数，计算集合中每个点的核心距离及对应的可达距离。

1) 初始化2个队列矩阵，用作储存种子队列和结果队列。

2) 判断集合中的数据点是否已经完全处理，如果完成，就结束算法，否则随机添加一个未经处理的数据点到种子队列开始步骤3)。

3) 若种子队列为空，跳转步骤2)，若非空，从种子队列中取出第一个点做拓展处理，若该点不存在于结果队列中，则将该点按可达距离排序插入到结果队列中。

①若种子队列中取出第一个点是核心对象，计算与该点有关的所有直接密度可达点，如果不是，重复进行步骤3)；②若通过计算比较，结果队列中已经不存在任何与该拓展点有关的直接密度可达点，进行步骤3)，否则继续等待；③ 若结果队列在之前已存储过与该点有关的直接密度可达点，但新计算的可达距离相比旧值更小，则予以替换，重新调整结果队列；④若结果队列中不存在与该点有关计算的直接密度可达点，则将该点按序插入结果队列中。

4) 算法结束，输出的结果队列即为可达序列。

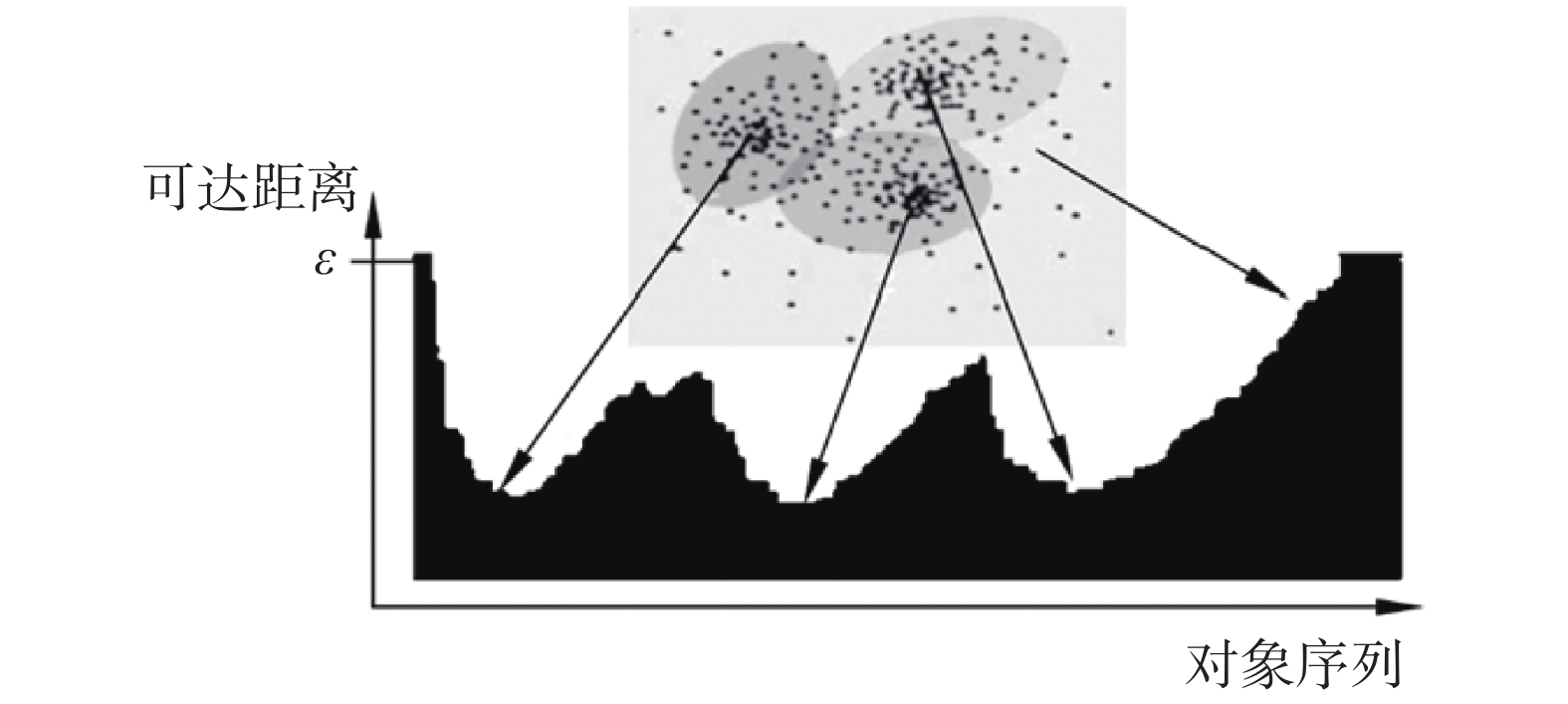
OPTICS算法聚类结果如图2所示。

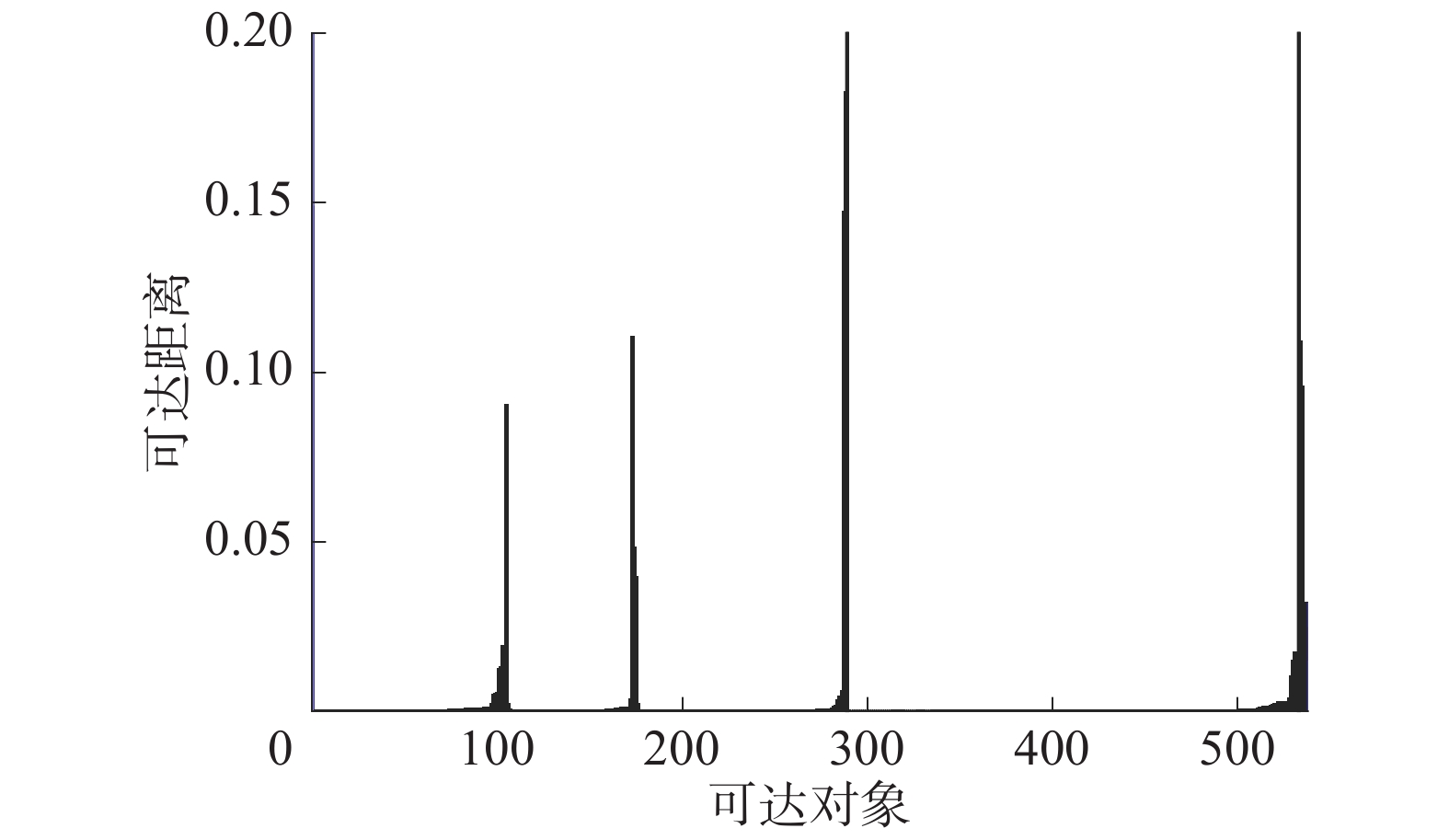
图2为通过OPTICS算法进行密度结构分析的结果，反映了可达距离与可达对象序列的关系，可以对数据进行密度结构分析，可达距离会随着对象序列的疏密程度呈现出高低分布，每个波谷的位置对应一个数据中心，波峰对应位于相邻2个数据中心之间的散点，波峰与波谷的距离差距越大表示数据的离散程度越大。因此通过对数据的密度结构分析，可以在先验信息不足的条件下，确定数据大致聚类中心以及聚类数目。

2.3 基于密度结构分析的改进FCM聚类算法

1) 初始参数优化

FCM算法优化的核心之一是对初始参数的优化，包括初始聚类中心和聚类数目。前面介绍了基于OPTICS算法的密度结构分析，通过OPTICS算法最终输出反映了数据密度结构的可达序列。可达序列中波谷的位置即为数据的聚类中心，因此对得到的可达距离序列进行波谷搜寻便可确定具体的聚类数目和大致的聚类中心。确定这2项参数，将这2项参数作为初始参数应用在FCM算法的聚类中可以解决FCM算法过于依赖初始聚类中心和聚类数目的缺陷。

2) 目标函数优化

FCM算法优化的另一个核心是尽可能地消除孤立散点导致的聚类中心偏移。OPTICS密度结构分析输出的可达序列另一项重要属性是和数据的离散程度有关，可达距离序列反映了每个样本点与相邻聚类中心离散程度。对孤立散点最理想的优化做法是尽量根据散点的离散情况来分配其在聚类中心隶属度划分的权重，即远离聚类中心的散点不会或者尽可能小地影响聚类中心的确定，而靠近聚类中心的散点会直接影响最终的聚类中心确定。这里可以考虑把可达序列作为离散动态加权因子对FCM的目标函数进行修正。

假设OPTICS算法聚类之后得到的可达距离序列为L，把可达距离序列作为动态加权系数对式(6)进行修正，修正后的目标函数为

$J({{U}},C) = \sum\limits_{i = 1}^c {\sum\limits_{j = 1}^n {u_{ij}^m} } {\left\| {{x_j} - {c_i}} \right\|^2}{L_j},1 \leqslant m < \infty {\text{}}$

(12)

当数据点远离聚类中心时，可达距离增大，算法无法收敛；当数据点靠近聚类中心时，可达距离变小，算法快速收敛。通过这一加权策略，可以提高算法的收敛速度，防止聚类中心偏移，从而有效改善噪点对聚类结果的影响。

利用Lagrange函数对式(12)进行重新构建，对u_ij和c_i求偏导得到式(13)和式(14)

$\frac{{\partial J}}{{\partial {u_{ij}}}} = mu_{ij}^{m - 1}{\left\| {{x_j} - {c_j}} \right\|^2}{L_j} - {\lambda _j} = 0{\text{}}$

(13)

$\frac{{\partial J}}{{\partial {c_i}}} = \sum\limits_{j = 1}^N {u_{ij}^m} ( - 2)\left( {{x_j} - {c_i}} \right){L_j} = 0{\text{}}$

(14)

进一步求得聚类中心C和隶属度矩阵U为

${c_i} = \frac{{\displaystyle\sum\limits_{j = 1}^n {u_{ij}^m} {x_j}{L_j}}}{{\displaystyle\sum\limits_{j = 1}^n {u_{ij}^m} {L_j}}}{\text{}}$

(15)

${u_{ij}} = \dfrac{1}{{\displaystyle\sum\limits_{k = 1}^c {{{\left[ {\dfrac{{{d_{ij}}}}{{{d_{kj}}}}} \right]}^{\frac{2}{{m - 1}}}}} }}{\text{}}$

(16)

基于密度结构分析的改进FCM算法步骤总结如下。

1) 用OPTICS算法对样本点进行密度结构分析，得到可达距离 $L$ ，并通过波谷搜索，确定聚类数目和初始聚类中心。

2) 用步骤1)中得到的聚类数目和聚类中心初始化FCM的聚类参数，并按照式(12)将可达距离 $L$ 作为动态加权因子对目标函数进行优化。

3) 根据式(15)和式(16)，并按照传统FCM聚类的迭代方法不断迭代，判断是否满足输出条件，最终求得隶属度矩阵U和聚类中心 $C$ 。

2.4 基于改进FCM算法的混合矩阵估计步骤

本文提出了基于密度结构分析的改进FCM算法，并利用这一算法实现了混合矩阵估计，具体的混合矩阵估计步骤如下。

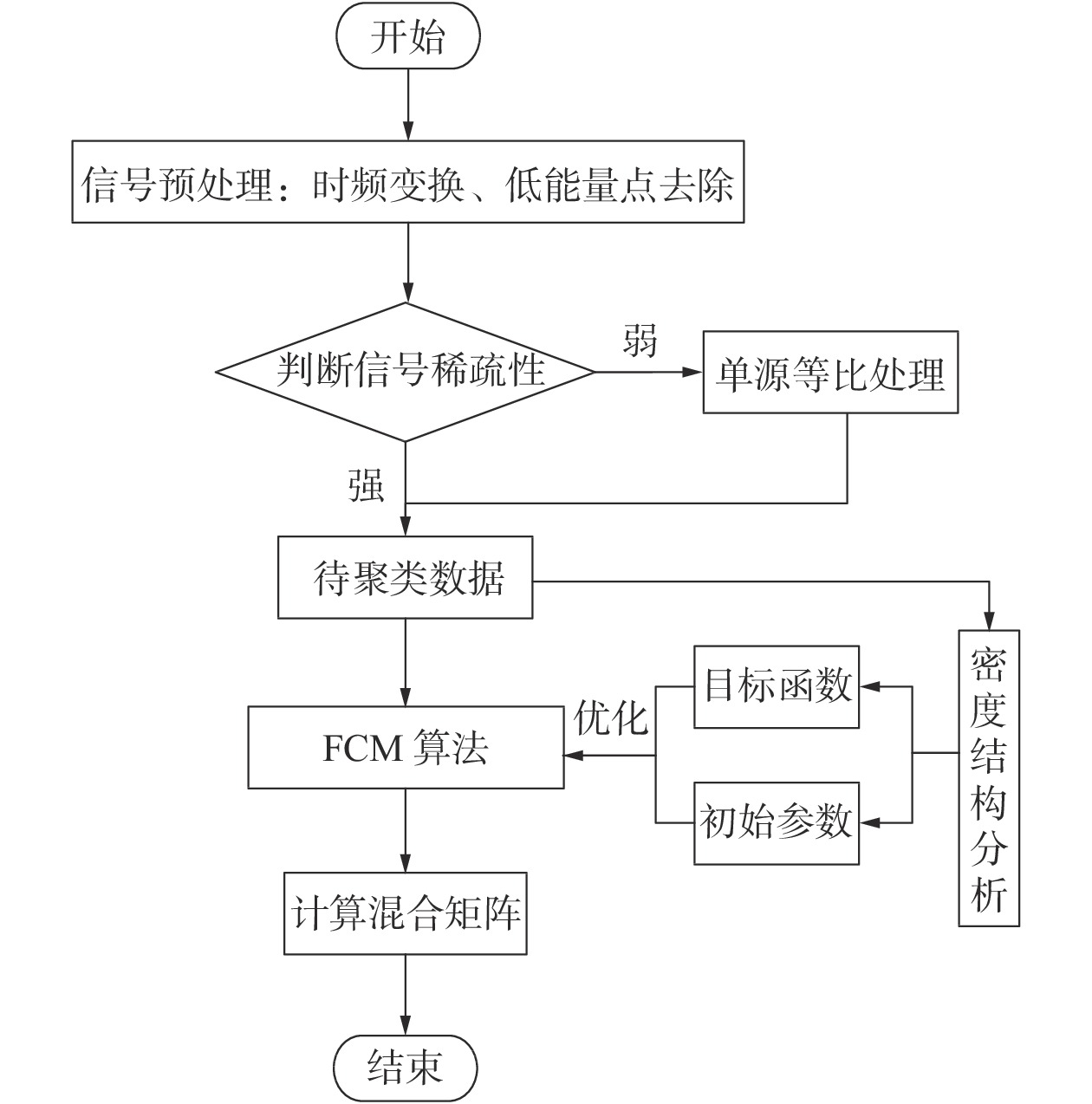
1) 对接收的混合信号进行预处理，包括时频变换和低能量点去除，得到信号的时频散点。

2) 判断信号稀疏性，若信号的稀疏性较差且冗余散点过多，对信号进一步做单源等比处理，增强信号的线性聚集性。

3) 对单源等比处理后的数据密度结构分析，从目标函数和初始参数两方面对FCM算法进行优化，并用优化后的算法进行聚类。

4) 用得到的聚类结果计算混合矩阵。

基于改进FCM算法的混合矩阵估计流程如图3所示。

3 仿真实验及结果分析 3.1 混合矩阵评估准则

本文采用以下2个标准来对估计混合矩阵的性能进行评估。

1) 归一化均方误差(normalized mean square error，NMSE，在公式中用N_MSE表示），数学表达式为

$N_{\rm{MSE}} = 10{\log _{10}}\left( {\frac{{\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^n {{{\left( {{{\hat a}_{ij}} - {a_{ij}}} \right)}^2}} } }}{{\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^n {a_{ij}^2} } }}} \right){\text{}}$

(17)

归一化均方误差越小说明矩阵估计性能越高，所估计出的混合矩阵越接近原混合矩阵。

2) 偏离角度，表达式为

$ \mathrm{ang}(a,\widehat{a})=\frac{180}{{\text{π}} }\mathrm{arccos}\left(\frac{<a,\widehat{a}>}{\Vert a\Vert \cdot \Vert \widehat{a}\Vert }\right){\text{}}$

(18)

式中：a为原混合矩阵A的列矢量； $\widehat{a}$ 为得到的估计矩阵 $\widehat{{{A}}}$ 中与a对应的列矢量。

偏离角度反映了原矩阵与估计矩阵之间的角度偏离情况，这个数值越小时，说明2个矩阵之间的相似度越高，越有助于最终的源信号重构。

3.2 实验仿真及分析

实验选用语音信号作为源信号，具体来源可参考 http://www.speech.cs.cmu.edu/cmu_arctic/。从中随机截取4段语音数据作为实验数据，长度为48 000，采样频率为16 kHz。选取的源信号如图4所示。

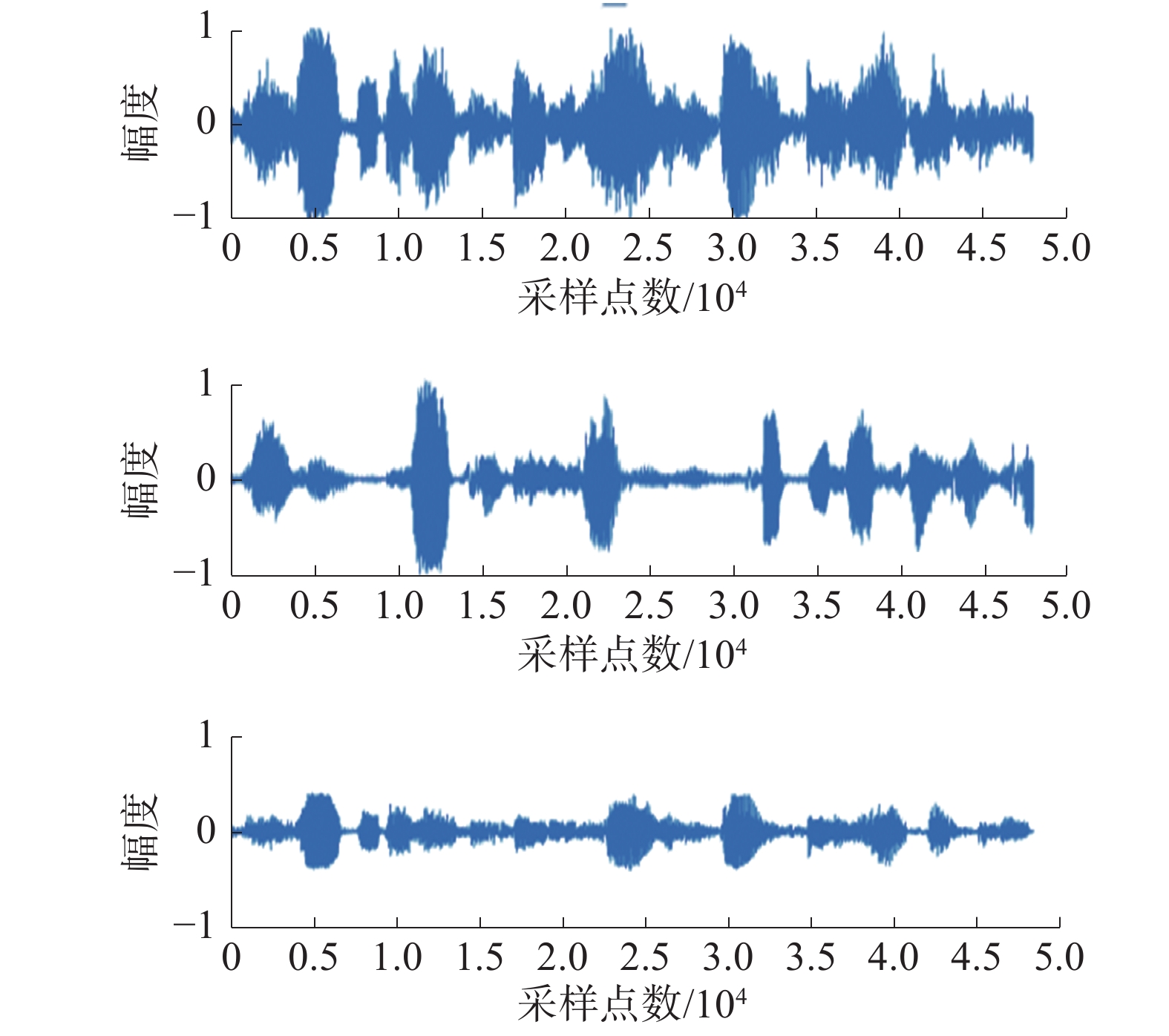
经过式(19)中的混合矩阵得到如图5所示的观测信号。

${{A}} = \left[ {\begin{array}{*{20}{c}} { - 0.891\;5}&{0.579\;8}&{ - 0.755\;0}&{0.924\;5} \\ {0.026\;7}&{0.813\;5}&{ - 0.375\;7}&{ - 0.242\;1} \\ {0.452\;3}&{0.045\;3}&{ - 0.537\;4}&{0.294\;3} \end{array}} \right]{\text{}}$

(19)

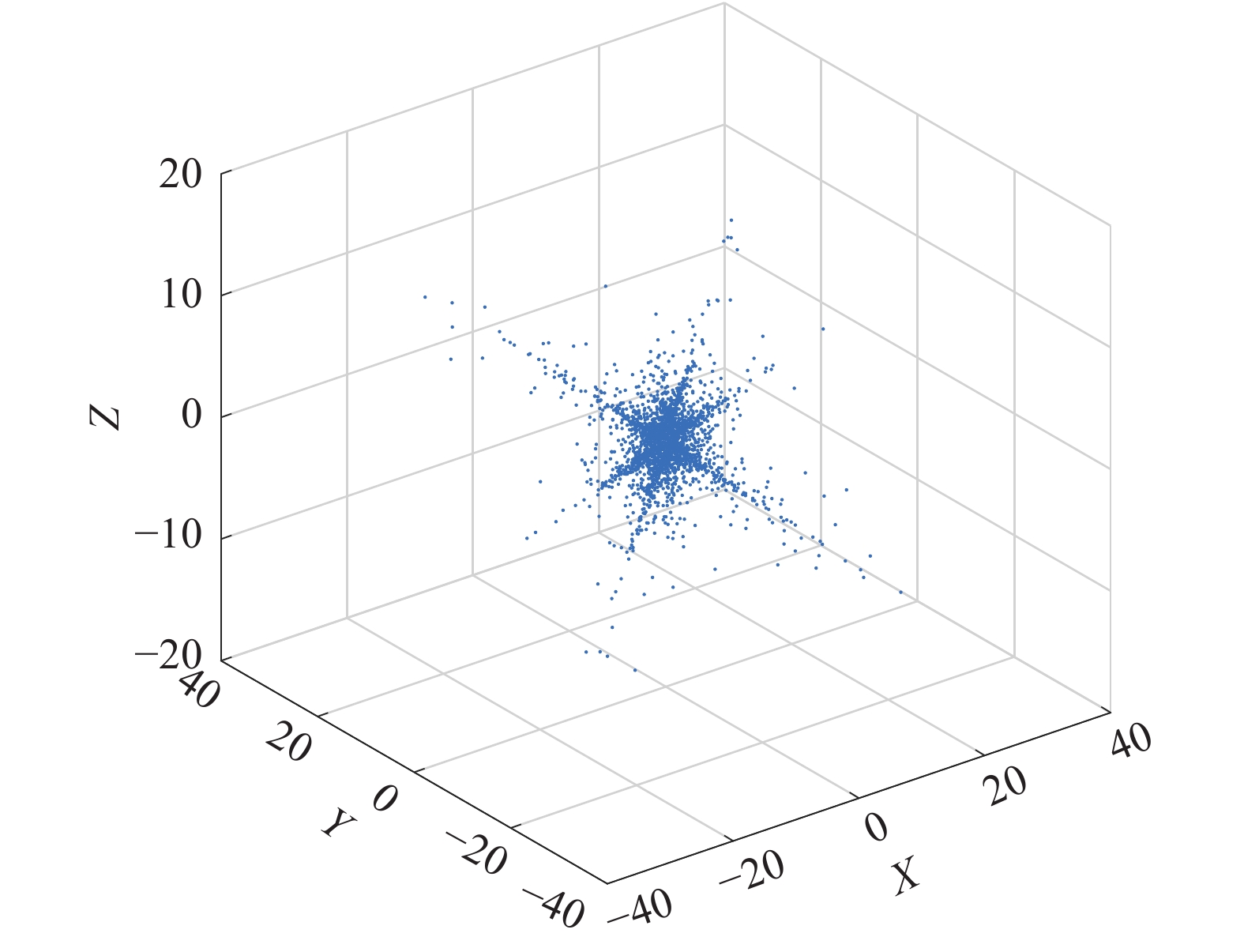
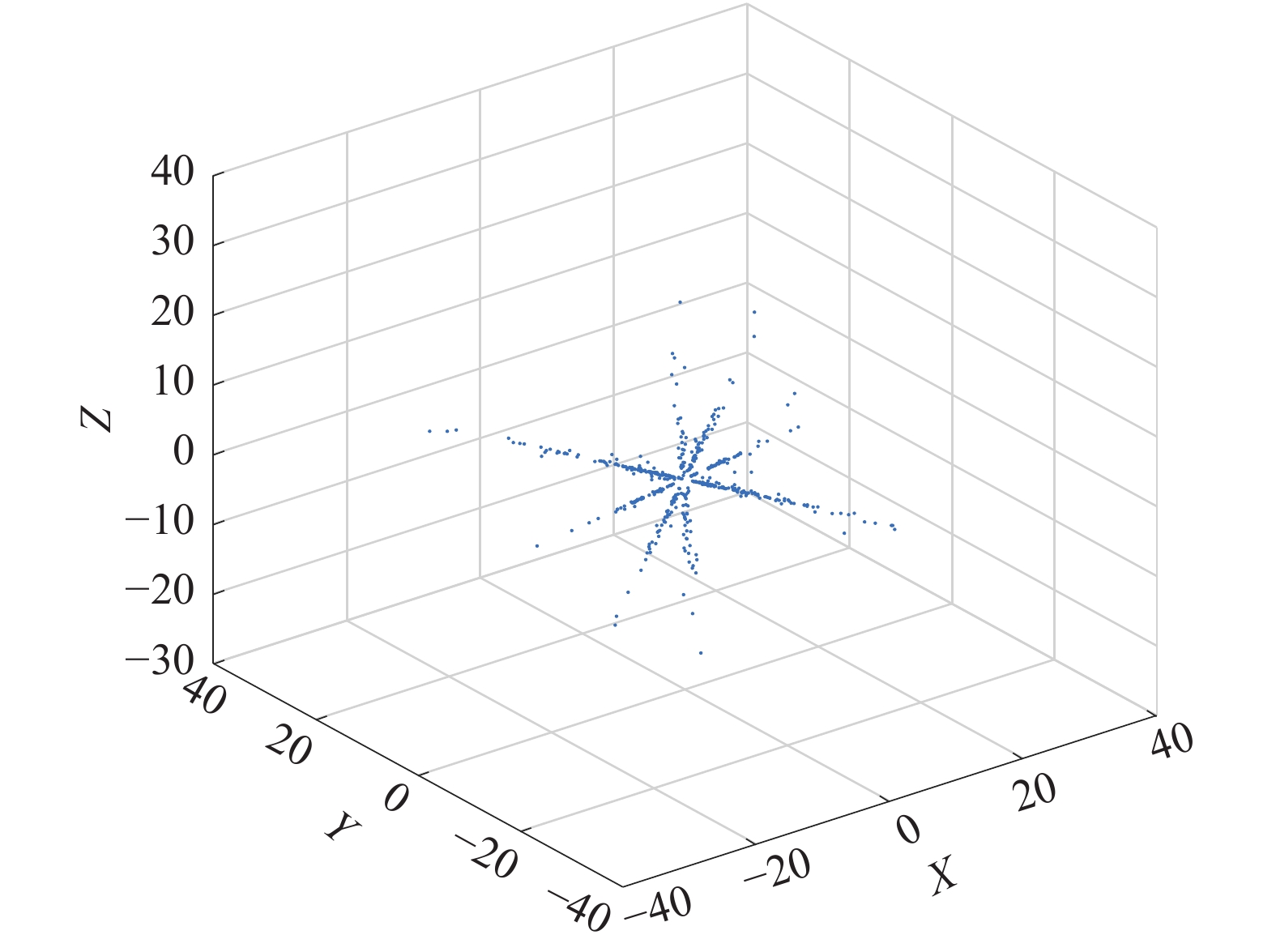
对观测信号进行预处理，时频变换这里选用短时傅立叶变换，窗函数选用Hanning窗，窗口长度设定为512，叠合长度为256，低能量去除的阈值取0.1。最终预处理后的散点图如图6所示。由图6可以看出通过时频变换，信号在时频域呈现出一定的方向性，但是冗余散点过多，需要进一步做单源等比处理去除冗余散点，结果如图7所示。

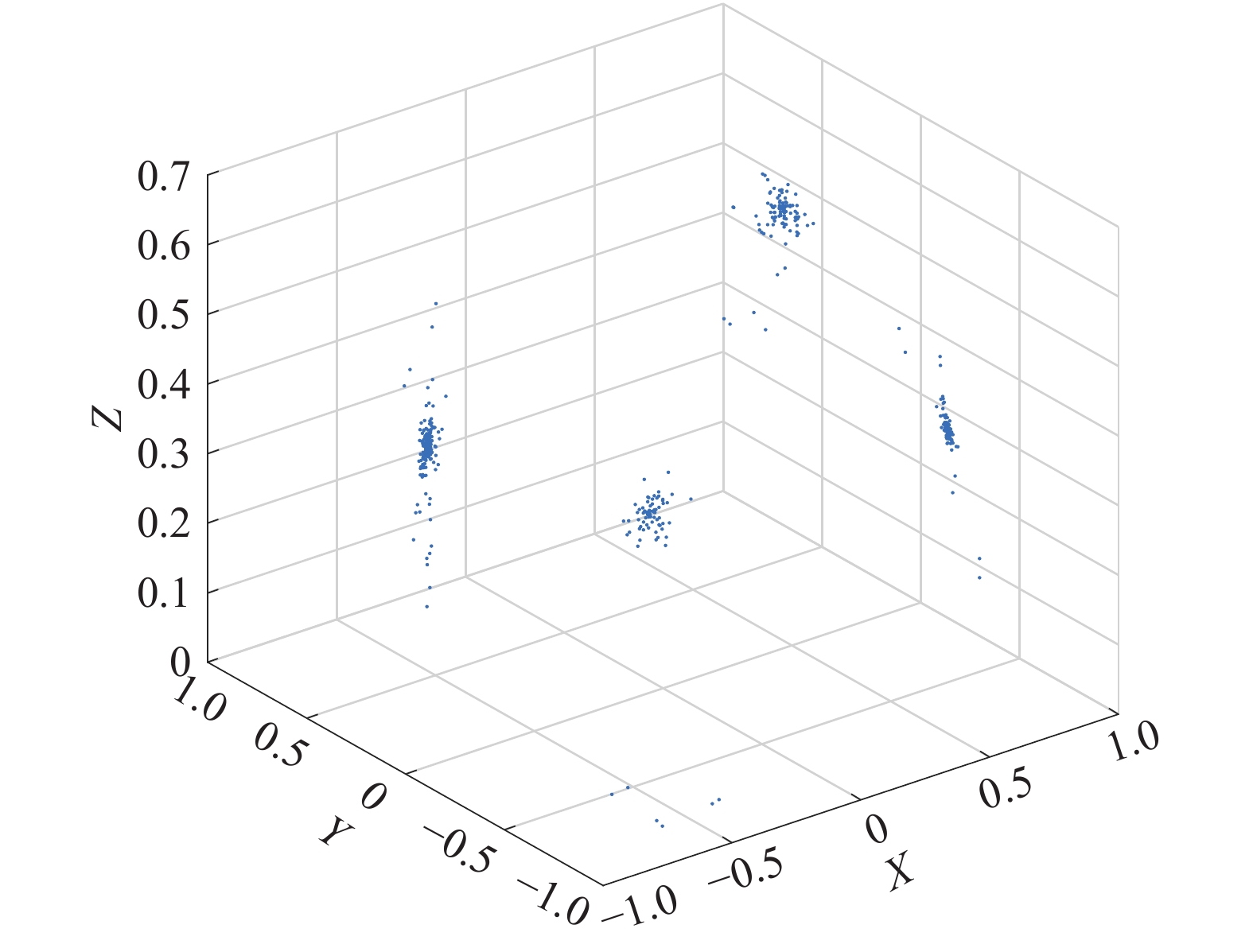
单源等比后数据的线性聚集性增强，为了方便聚类，对样本数据做归一化处理，将所有散点映射到球面上，归一化结果如图8所示。

用OPTICS算法对归一化后的数据进行密度结构分析，结果如图9所示。从图9中可以看出聚类数目为4，初始聚类中心可从波谷处的位置选取，以此2项参数为基础实现对FCM初始参数的优化。

分别用基于密度结构分析的改进FCM算法和传统FCM算法对单源等比后的数据集进行聚类对比，横向比较聚类成功率，其中传统FCM初始参数(聚类中心、聚类数目)的设置为随机选取。在样本数据保持不变的情况下，分别重复进行100次聚类，统计聚类成功次数如表1所示。

实验结果表明，传统的FCM算法由于初始聚类中心和聚类数目选用规则为随机选取，因此会出现一定概率的聚类失败，但通过本文的改进方法可以实现对初始参数的优化，避免因初始参数的设置不当而导致的聚类失败。

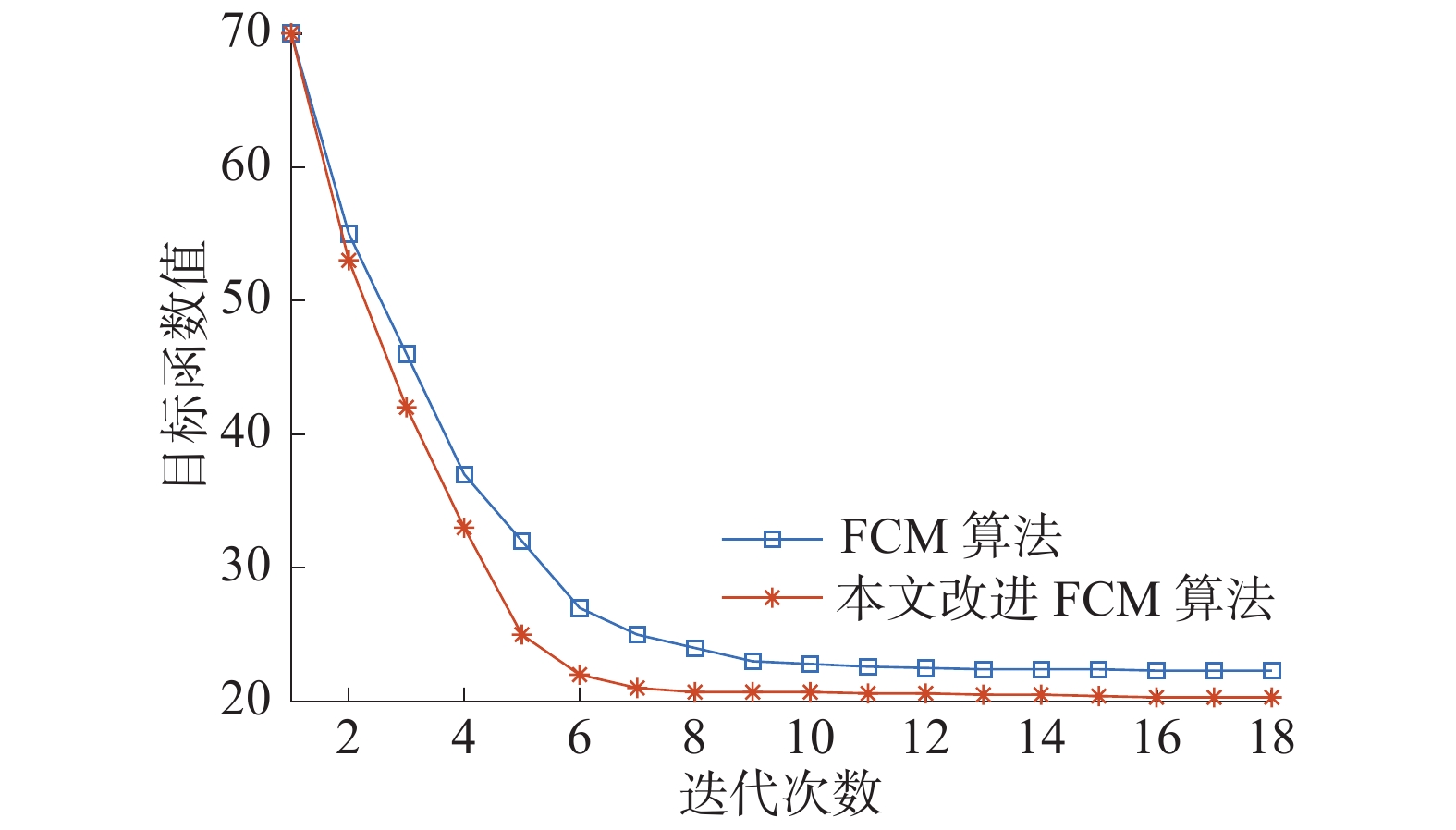
再对2种算法的迭代次数进行对比，结果如图10所示。

迭代次数和目标函数收敛情况表明，得益于对目标函数的优化，本文改进算法相比于传统FCM算法有着更低的迭代次数和更快的收敛速度，同时目标函数值也略有降低，能带来更好的聚类效果。

在聚类成功的基础上，利用改进的聚类算法估计混合矩阵，并选用2种经典的聚类算法K-means算法与FCM算法作为对比。

K-means算法估计出的混合矩阵为

${{{A}}_{{\rm{K - means}}}} = \left[ {\begin{array}{*{20}{c}} { - 0.876\;1}&{0.574\;9}&{ - 0.741\;8}&{\;\;0.934\;2} \\ {\;\;0.025\;9}&{0.817\;8}&{ - 0.376\;9}&{ - 0.224\;1} \\ {\;\;0.481\;4}&{0.026\;3}&{ - 0.554\;7}&{\;\;0.277\;6} \end{array}} \right]$

(20)

FCM算法估计出的混合矩阵为

${{{A}}_{{\rm{FCM}}}} = \left[ {\begin{array}{*{20}{c}} { - 0.873\;2}&{0.573\;8}&{ - 0.749\;3}&{\;\;0.936\;3} \\ {\;\;0.025\;5}&{0.817\;8}&{ - 0.372\;1}&{ - 0.215\;5} \\ {\;\;0.476\;7}&{0.044\;1}&{ - 0.547\;8}&{\;\;0.277\;3} \end{array}} \right]$

(21)

本文提出的算法估计出的混合矩阵为

${{A}} = \left[ {\begin{array}{*{20}{c}} { - 0.891\;1}&{0.582\;5}&{ - 0.753\;4}&{\;\;0.921\;6} \\ {\;\;0.021\;3}&{0.811\;7}&{ - 0.371\;1}&{ - 0.258\;3} \\ {\;\;0.453\;3}&{0.041\;6}&{ - 0.542\;8}&{\;\;0.289\;7} \end{array}} \right]$

(22)

根据上面估计的混合矩阵，结合性能评估准则，计算归一化均方误差和偏离角度如表2和表3所示。

首先对比归一化均方误差，从表2可以看出，改进后的FCM算法相对于传统FCM算法和K-means算法可使归一化均方误差最少减小6 dB。然后对比偏离角度，表3中的数据表明了估计矩阵与混合矩阵之间的夹角偏离情况，可以看出改进的FCM算法计算出的矩阵偏离角度相对于传统方法得到的偏离角度最多可减少1.5°。两项对比结果均表明，由于本文对FCM算法初始参数和目标函数的双重优化，最终估计出的混合矩阵精度和性能都得到提高。

4 结论

本文提出了一种基于密度结构分析的改进FCM聚类算法，并将这一改进算法用于盲源分离的混合矩阵估计中。本文的改进算法针对传统FCM算法存在的问题，通过密度结构分析确定了正确的聚类数目和大致的初始聚类中心，实现对FCM算法初始参数的优化，同时输出的可达距离序列作为加权因子应用到FCM目标函数中，从而降低噪点对聚类结果的影响，实现对目标函数的优化。实验结果和理论分析说明了文中模型、方法的有效性。