近年来，非能动设计理念已经开始应用到大型先进压水堆中，华龙一号(HPR1000)以及国和一号(CAP1400)均采用了非能动设计。发生严重事故时，该设计主要是通过实施反应堆压力容器外部冷却(external reactor vessel cooling，ERVC)达到熔融物堆内滞留(IVR)，保证放射性物质不释放到环境中。IVR-ERVC实施过程中，能否顺利通过自然循环带走多余的衰变热是保障反应堆安全的核心要务。而自然循环措施成功实施的关键在于压力容器外部的热通量小于当地的临界热流密度(CHF)。

目前，国内外的学者已经对CHF进行了大量的实验和理论研究，取得了大量的实验数据并且建立了相应的经验关系式。刘瑞兰等^[1]对间隙1.0 mm的环形狭缝中低质量流量下饱和沸腾强迫循环的换热特性进行了实验研究。杨震等^[2]在微液层模型的基础上，利用气液守恒关系推导出两相边界层的初始厚度，选取最大夹带系数时的空泡份额对下封头饱和池式沸腾时的CHF进行理论预测。周磊等^[3]通过优化DRYOUT模型中重要本构关系式组合，适当选取沉积率和夹带率公式得到适用于矩形窄缝通道的DRTOUT模型。张亚培等^[4]分析了倾角变化的矩形通道内CHF的特点，并建立了适用于矩形窄缝通道的CHF理论模型，该模型考虑了倾角变化对CHF的影响。封坤等^[5]以气液两相逆向对流限制机理为基础，建立了球形窄缝通道的CHF理论模型，并进一步分析了系统半径、熔融物半径和间隙尺寸等参数对CHF的影响。陈薇等^[6]建立了机理性试验平台对加热表面朝下倾斜矩形通道内的流量波动对CHF的影响进行试验，总结出流量波动周期、振幅对CHF的影响。郭锐^[7]通过观察不同倾角下气泡的运动特征并结合试验现象，在气泡壅塞模型基础上，建立了IVR-ERVC条件下的CHF机理模型并对瞬态进程中的CHF分布进行了计算，以评估严重事故瞬态进程中IVR措施的有效性。Cheung等^[8]利用SBLB试验装置进行了池式沸腾试验并推导出适用于下封头外表面的池式沸腾CHF关系式。

本文在Cheung等^[8]的水动力不稳定性及宏液膜理论模型基础上，建立了朝下表面矩形通道在过冷低质量流速条件下的CHF机理模型，该模型将加热壁面附近的流场分为4个区域，同时通过能量及质量守恒求解出各层的流动参数，对IVR-ERVC条件下的临界热流密度进行预测分析，重点研究了发生CHF时，质量流速和流道深度对CHF的影响，分析了不同质量流速及倾角变化对当地气泡长度及气泡速度的影响。

1 数学模型 1.1 基础模型

压力容器下封头发生CHF时，由于水位高度的原因会造成入口水温低于当地的饱和温度，随着倾角的增加，两相边界层的厚度也会逐渐增加。当地发生CHF时，贴近壁面区域产生的气泡会有一部分被过冷主流区冷凝。为与实际情况相符合，本文建立的CHF模型基于以下假设：

1)由于受力和聚合的作用，紧贴加热壁面处存在较大的细长的变形气泡；

2)加热壁面与贴壁气泡之间存在宏液膜，并且其厚度与过冷度存在关系；

3)两相边界层阻碍了主流液体与加热壁面之间的换热；

4)当上游流入和主流区扩散至加热壁面的液体质量小于蒸发消耗量时，发生CHF；

5)宏液膜的厚度随着当地热流密度的增加而增加，当发生CHF时，液膜厚度达到最大。

在加热壁面附近的细长的大气泡下面有一个宏液膜。宏液膜由一系列液体薄膜组成，液膜内含有蒸汽柱。在稳定的饱和沸腾条件下，气柱的质量流速等于泡核沸腾量。该模型将流场分为加热壁面附近的宏液膜区、大气泡所在的气泡层、气泡中部的两相区和远离壁的单相区4个部分，如图1所示。

宏液膜、气泡层和两相区共同构成了两相边界层。

宏液膜中的质量流量可表示为

${m_{\rm{s}}} = {\rho _{\rm{l}}}{u_{{\rm{lm}}}}{A_{\rm{m}}}$

(1)

式中： ${m_{\rm{s}}}$ 为来自上游的液体补充速率， ${\rho _{\rm{l}}}$ 为液体密度， ${u_{{\rm{lm}}}}$ 为宏液膜内的液相有效速度， ${A_{\rm{m}}}$ 为加热表面和大气泡之间的横截面积。

在大气泡下，宏观液膜中的蒸发质量率可以表示为

${m_{\rm{d}}} = \frac{{{q_\theta }{A_{\rm{w}}}}}{{{h_{{\rm{fg}}}}}}$

(2)

式中： ${m_{\rm{d}}}$ 为质量蒸发速率， ${q_\theta }$ 为核态沸腾热通量切向分量， ${A_{\rm{w}}}$ 为大气泡下的加热壁面积， ${h_{{\rm{fg}}}}$ 为汽化潜热。

结合式(1)和式(2)，可以得到：

${q_\theta } = {\rho _{\rm{l}}}{u_{{\rm{lm}}}}{h_{{\rm{fg}}}}\frac{{{A_{\rm{m}}}}}{{{A_{\rm{w}}}}}$

(3)

式中：

${A_{\rm{m}}} = {\delta _{\rm{m}}}{w_{\rm{b}}}$

(4)

${A_{\rm{w}}} = {L_{\rm{b}}}{w_{\rm{b}}}$

(5)

式中： ${\delta _m}$ 为宏液膜的厚度， ${L_{\rm{b}}}$ 为细长的气泡长度， ${w_{\rm{b}}}$ 为壁面宽度。

将式(4)和式(5)代入式(3)可得

${q_\theta } = {\rho _{\rm{l}}}{u_{{\rm{lm}}}}{h_{{\rm{fg}}}}\frac{{{\delta _{\rm{m}}}}}{{{L_{\rm{b}}}}}$

(6)

由式(6)可以看出，影响传热的独立变量是宏液膜内的液相流速、宏液膜的厚度和大气泡长度。

矩形通道中液相和气相质量的守恒方程为

$ \begin{aligned} & \left[ {{\rho _{\rm{l}}}{u_{{\rm{lm}}}}\left( {1 - {\alpha _{\rm{m}}}} \right) + {\rho _{\rm{g}}}{u_g}{\alpha _{\rm{m}}}} \right]{\delta _{\rm{m}}} + \left[ {{\rho _{\rm{l}}}{u_{{\rm{lb}}}}\left( {1 - {\alpha _{\rm{b}}}} \right) + {\rho _{\rm{g}}}{u_{\rm{g}}}{\alpha _{\rm{b}}}} \right]{D_{\rm{b}}} + \\ & \left[ {{\rho _{\rm{l}}}{u_{{\rm{ls}}}}\left( {1 - {\alpha _{{\rm{tw}}}}} \right) + {\rho _{\rm{g}}}{u_{\rm{g}}}{\alpha _{{\rm{tw}}}}} \right]\left( {\delta - {D_{\rm{b}}} - {\delta _{\rm{m}}}} \right) + {\rho _{\rm{l}}}{u_{{\rm{ls}}}}\left( {H - \delta } \right) = G \cdot H \end{aligned} $

式中： ${u_{{\rm{lm}}}}$ 、 ${u_{{\rm{lb}}}}$ 和 ${u_{{\rm{ls}}}}$ 分别为宏液膜内液相速度、气泡中心液相速度、两相区和单相区的液相速度， ${\alpha _m}$ 、 ${\alpha _b}$ 和 ${\alpha _{tw}}$ 分别为宏液膜内空泡份额、气泡层内空泡份额和两相区内空泡份额， $\delta $ 为两相边界层的厚度，H为当地矩形通道高度，G为当地截面平均质量流量。

当大气泡的浮力超过了周围流体的阻力和表面张力时，大气泡开始脱离加热壁面，这个循环过程在高热通量下不断重复，从气泡开始产生到离开之间的时间称为悬停时间。为了获得切向分量，必须首先确定两相边界层的厚度。两相边界层中的气相部分由两相区和单相区扩散进入到宏液膜内的液相受热蒸发而来，因此，单位时间内扩散入宏液膜内的液相质量有如下关系：

${m_{\rm{k}}} = \frac{{{q_{\rm{r}}}}}{{h{}_{{\rm{fg}}}}}$

认为 $\tau $ 时间内，扩散到两相区热量 ${q_{\rm{r}}}$ 与两相边界层厚度 $\delta $ 之间存在如下关系：

${q_{\rm{r}}}\tau = {E_0}{\rho _{\rm{l}}}{h_{{\rm{fg}}}}\alpha \delta $

式中： $\tau $ 为大气泡悬停时间； ${q_{\rm{r}}}$ 为两相边界层中总相变热量的 ${E_0}$ 倍， $0 \leqslant {E_0} \leqslant 1$ 。

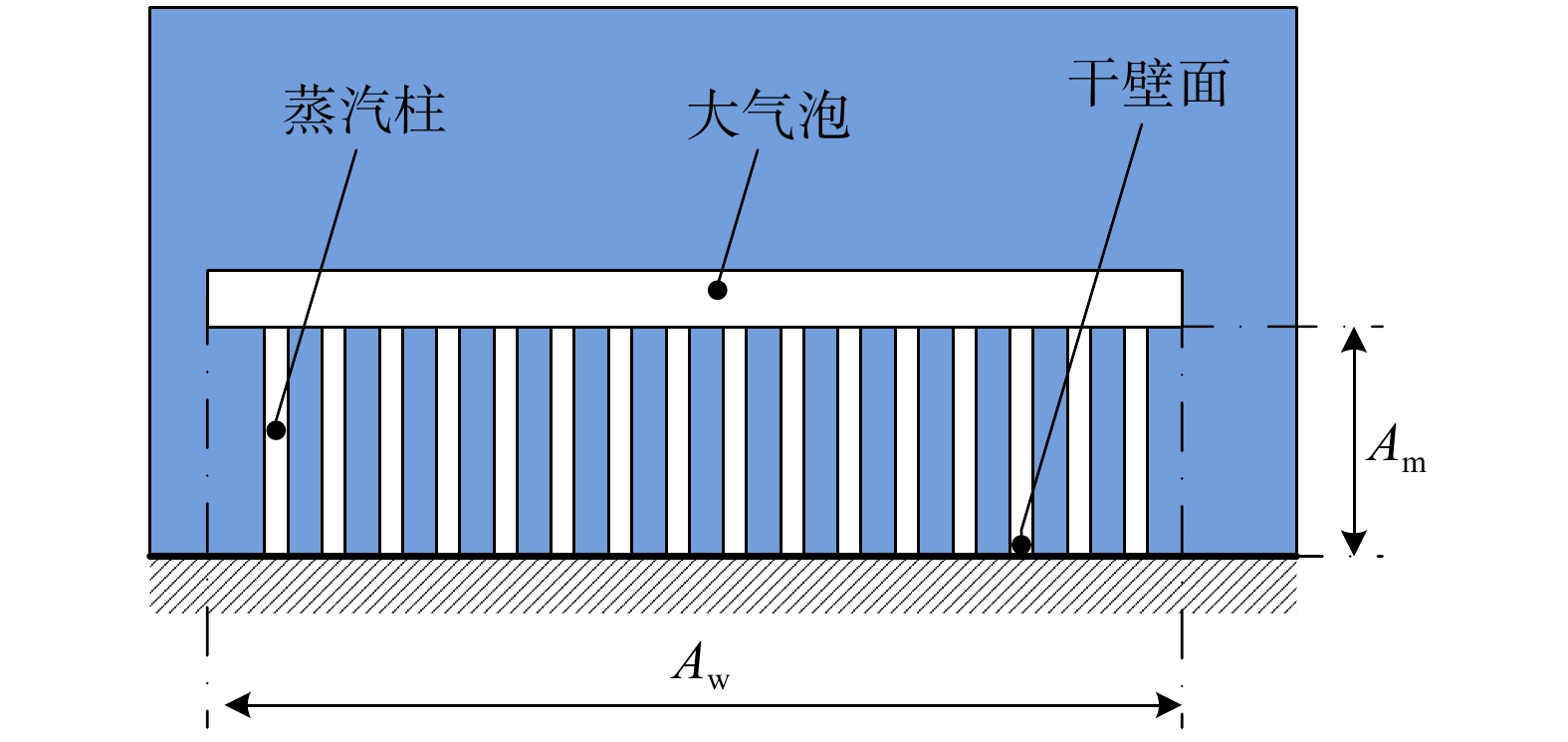
图2是宏液膜蒸干模型示意图，宏液膜内部的波状气柱可以近似看作圆柱形，宏液膜内的空泡份额近似等于蒸汽柱面积 ${A_{\rm{g}}}$ 与气泡下加热壁面积的比值，于是：

${\alpha _{\rm{m}}} \approx \frac{{{A_{\rm{g}}}}}{{{A_{\rm{w}}}}}$

Cheung等^[9]认为在池沸腾饱和工况发生CHF时的空泡份额为0.915，所以在本文中认为发生CHF时，大气泡区域的空泡份额为0.915，即 ${\delta _{\rm{m}}} \leqslant y < {\delta _{\rm{m}}} + {D_{\rm{b}}}$ ，单相区内的气泡很少，空泡份额近似为0。各层平均空泡份额分布如下：

$\alpha = \left\{ {\begin{array}{*{20}{l}} {\displaystyle\frac{{{A_{\rm{g}}}}}{{{A_{\rm{w}}}}},}\quad\quad{0 \leqslant y < {\delta _{\rm{m}}}} \\ {0.915,}\quad\quad{{\delta _{\rm{m}}} \leqslant y < {\delta _{\rm{m}}} + {D_{\rm{b}}}} \\ {0.458,}\quad\quad{{\delta _{\rm{m}}} + {D_{\rm{b}}} \leqslant y < \delta } \end{array}} \right.$

式中 $y$ 为离壁面的距离。当 $y = {\delta _{\rm{m}}} + {D_{\rm{b}}}$ 时， $\alpha = 0.915$ ；当 $y = \delta $ 时， $\alpha = 0$ 。

从宏液膜边界 ${\delta _{\rm{m}}}$ 到变形气泡中心 ${\delta _{\rm{m}}} + \displaystyle\frac{{{D_{\rm{b}}}}}{2}$ 处，空泡份额单调递增。Bloch 等^[10]通过实验得出，发生CHF时，空泡份额与壁面距离线性相关。这里认为， ${\delta _{\rm{m}}} + {D_{\rm{b}}}$ 到两相边界层边界 $\delta $ 处，空泡份额的值由0.915单调递减为0。

由以上可知，宏液膜内空泡份额为 ${\alpha _{\rm{m}}} = \displaystyle\frac{{{A_{\rm{g}}}}}{{{A_{\rm{w}}}}}$ ， ${\delta _{\rm{m}}}$ 到 ${\delta _{\rm{m}}} + {D_{\rm{b}}}$ 处空泡份额均值 ${\alpha _{\rm{b}}} = 0.915$ ， ${\delta _{\rm{m}}} + {D_{\rm{b}}}$ 到两相边界层边界 $\delta $ 处空泡份额均值为 ${\alpha _{{\rm{tw}}}} = \displaystyle\frac{{0.915}}{2} = 0.458$ 。

1.2 蒸汽柱面积比例计算

对于理想的无穷大壁面，气泡从泰勒波的波峰处产生，临界泰勒波长为最危险波长，临界泰勒波长可表示为

${\lambda _{\rm{D}}} = 2{\text π}\sqrt 3 {\left( {\frac{\sigma }{{g\left( {{\rho _{\rm{l}}} - {\rho _{\rm{g}}}} \right)}}} \right)^{0.5}}$

假设每一个波长平方内的加热壁面产生一个气泡，则单位时间内提供给气泡的蒸汽体积为

$V = \frac{{{q_\theta }\lambda _{\rm{D}}^2}}{{{\rho _{\rm{g}}}{h_{{\rm{fg}}}}}}$

气泡悬停时间和蒸汽体积有着如下关系^[11]：

${\tau _{\rm{d}}} = {\left( {\frac{3}{{4{\text π}}}} \right)^{0.2}}{\left[\begin{split} {\frac{{4\left( {\displaystyle\frac{{11}}{{16}}{\rho _{\rm{l}}} + {\rho _{\rm{g}}}} \right)}}{{\left( {{\rho _{\rm{l}}} - {\rho _{\rm{g}}}} \right)g}}} \end{split}\right]^{0.6}}{V^{0.2}}$

式中系数11/16是气泡移动时所携带液体的体积比例。

大气泡阻碍主流区液体与巨液膜的接触。因此，液膜的厚度由于蒸发而逐渐减薄。沸腾危机发生时，液膜完全干化的时间刚好等于气泡悬停的时间。也就是说，气泡离开时，液膜刚好完全干化。从能量平衡角度，在气泡悬停的时间内，加热壁面扩散进来的热量等于液膜完全蒸发的潜热。

${\tau _{\rm{d}}}{q_\theta }{A_{\rm{w}}} = {\rho _{\rm{l}}}{\delta _{\rm{m}}}\left( {{A_{\rm{w}}} - {A_{\rm{g}}}} \right){h_{{\rm{fg}}}}$

(7)

将 ${\tau _{\rm{d}}}$ 和 ${\delta _{\rm{m}}}$ 代入式(7)可得：

$\begin{aligned} \frac{{{q_\theta }}}{{{\rho _{\rm{g}}}{h_{{\rm{fg}}}}}} = & {\left( {\frac{{{{\text π}^4}}}{{{2^{11}} \times {3^2}}}} \right)^{0.0625}}{\left( {\frac{{{A_{\rm{g}}}}}{{{A_{\rm{w}}}}}} \right)^{0.625}}{\left( {1 - \frac{{{A_{\rm{g}}}}}{{{A_{\rm{w}}}}}} \right)^{0.3125}} \times \\ & {\left[ {\frac{{1 + \displaystyle\frac{{{\rho _{\rm{l}}}}}{{{\rho _{\rm{g}}}}}}}{{{{\left( {\displaystyle\frac{{11{\rho _{\rm{l}}}}}{{16{\rho _{\rm{g}}}}} + 1} \right)}^{0.6}}}}} \right]^{0.3125}}{\left[ {\frac{{\sigma g\left( {{\rho _{\rm{l}}} - {\rho _{\rm{g}}}} \right)}}{{\rho _{\rm{g}}^2}}} \right]^{0.25}} \end{aligned} $

Zuber的水动力不稳定性临界热流密度模型适用于本实验，且 $\displaystyle\frac{{{A_{\rm{g}}}}}{{{A_{\rm{w}}}}} < < 1$ ，所以：

$1 - \frac{{{A_{\rm{g}}}}}{{{A_{\rm{w}}}}} \approx 1$

(8)

令 ${q_\theta } = 0.131{\rho _{\rm{g}}}h_{{\rm{fg}}}^{0.5}{\left[ {\sigma g\left( {{\rho _{\rm{l}}} - {\rho _{\rm{g}}}} \right)} \right]^{0.25}}$ 与式(8)中的热通量相等可得：

$\frac{{{A_{\rm{g}}}}}{{{A_{\rm{w}}}}} = 0.065\;38{\left[ {\frac{{{{\left( {\displaystyle\frac{{11{\rho _{\rm{l}}}}}{{16{\rho _{\rm{g}}}}} + 1} \right)}^{0.6}}}}{{1 + \displaystyle\frac{{{\rho _{\rm{l}}}}}{{{\rho _{\rm{g}}}}}}}} \right]^{0.5}}$

又因为 $ \displaystyle\frac{{{\rho _{\rm{g}}}}}{{{\rho _{\rm{l}}}}} < < 1$ ，所以：

$\frac{{{A_{\rm{g}}}}}{{{A_{\rm{w}}}}} = 0.058\;4{\left( {\frac{{{\rho _{\rm{g}}}}}{{{\rho _{\rm{l}}}}}} \right)^{0.2}}$

(9)

1.3 宏液膜厚度计算

高热通量时的大气泡与宏液膜已经被很多研究者证实发现^[12-15]，宏液膜的厚度随着热通量的增加而变薄，大气泡由于吸收宏液膜不断蒸发的热量，体积逐渐增大。当临界热通量发生时，在气泡悬停的时间内，加热壁面扩散进来的热量必须等于宏液膜完全蒸发时的潜热。

在宏液膜上的能量和质量平衡(假设来自加热器表面的能量完全被用于宏液膜蒸发，导致蒸汽形成)存在以下关系：

${q_{{\rm{nb}}}} = - {\rho _{\rm{l}}}{h_{{\rm{fg}}}}\left( {{A_{\rm{w}}} - {A_{\rm{g}}}} \right)\frac{{{\rm{d}}{\delta _{\rm{m}}}}}{{{\rm{d}}t}} = {\rho _{\rm{g}}}{v_{\rm{g}}}{A_{\rm{g}}}{h_{{\rm{fg}}}}$

式中： ${\rho _{\rm{g}}}$ 为蒸汽密度； ${\rho _{\rm{l}}}$ 为液体密度； ${v_{\rm{g}}}$ 为蒸汽喷口速度； ${v_{\rm{l}}}$ 为液体垂直流入加热面的速度； ${h_{{\rm{fg}}}}$ 为汽化潜热； ${q_{{\rm{nb}}}}$ 为当地核态沸腾热通量，CHF发生时 ${q_{{\rm{nb}}}} = {q_\theta }$ 。

在τ时间内，宏液膜完全蒸干，则临界热流密度条件下的条件为 $t = \tau $ ， ${\delta _{\rm{m}}} = 0$ 。所以：

${\delta _{{\rm{initial,m}}}} = \frac{{{\rho _{\rm{g}}}{v_{\rm{g}}}{A_{\rm{g}}}}}{{{\rho _{\rm{l}}}\left( {{A_{\rm{w}}} - {A_{\rm{g}}}} \right)}}\tau $

(10)

为了消除式(10)中蒸汽速度 ${v_{\rm{g}}}$ ，可以将亥姆霍兹不稳定性与宏观层的初始厚度联系起来。相对于气相速度，可以忽略液体速度，并假设宏液膜厚度是四分之一亥姆霍兹不稳定性波长，即

${\delta _{{\rm{initial,m}}}} = \frac{1}{4}{\lambda _{\rm{H}}}$

又根据亥姆霍兹不稳定性波长为

${\lambda _{\rm{H}}} = 2{\text π}\frac{{\left( {{\rho _{\rm{l}}} + {\rho _{\rm{g}}}} \right)\sigma }}{{{\rho _{\rm{l}}}{\rho _{\rm{g}}}{{\left( {{v_{\rm{g}}} - {v_{\rm{l}}}} \right)}^2}}}$

(11)

所以：

${v_{\rm{g}}} = \sqrt {\frac{{{\text π}\sigma \left( {{\rho _{\rm{l}}} + {\rho _{\rm{g}}}} \right)}}{{2{\rho _{\rm{l}}}{\rho _{\rm{g}}}{\delta _{{\rm{initial,m}}}}}}} $

(12)

将式(10)—式(12)联立，可以得出：

${\delta _{{\rm{initial,m}}}} = \frac{{{\rho _g}{A_g}}}{{{\rho _l}{A_w}}}{\left( {1{\rm{ - }}\frac{{{A_g}}}{{{A_w}}}} \right)^{ - 1}}\sqrt {\frac{{{\rho _l} + {\rho _g}}}{{{\rho _l}{\rho _g}}}\sigma } \tau $

(13)

从式(9)中可以看出，蒸汽柱面积和加热表面的比值是气相和液相密度比的函数。

将式(9)代入式(13)，可以得到：

$ {\delta _{{\rm{initial}}}} = 0.0584{\left( {\frac{{{\rho _g}}}{{{\rho _l}}}} \right)^{1.2}}{\left[ {1 - 0.0584{{\left( {\frac{{{\rho _g}}}{{{\rho _l}}}} \right)}^{0.2}}} \right]^{ - 1}}\sqrt {\frac{{{\rho _l} + {\rho _g}}}{{{\rho _l}{\rho _g}}}\sigma } \tau $

(14)

当单相区的部分过冷液体扩散进两相区，接触大气泡的上部时，一部分气体在大气泡内凝结，这会增加大气泡在壁面的悬停时间^[16-17]。

${\tau _{{\rm{sub}}}} = \frac{{\left( {1 + kJa} \right)\tau }}{{\left[ {1 + 0.102{{\left( {\displaystyle\frac{{{\rho _{\rm{g}}}}}{{{\rho _{\rm{l}}}}}} \right)}^{0.75}}Ja} \right]}}$

式中：Ja为雅各布数，它是液体相变(包括膜状换热和沸腾传热)时液体过热的热量与潜热的一种度量， $Ja = \displaystyle\frac{{{\rho _{\rm{l}}}{C_{\rm{p}}}\Delta {T_{{\rm{sub}}}}}}{{{\rho _{\rm{g}}}{h_{{\rm{fg}}}}}}$ ；k为经验系数，这里值取为1。

在式(14)中我们可以看到气泡悬停时间随着过冷水平的增加而增加。

1.4 变形气泡速度及长度计算

宏观液膜存在于反应堆压力容器壁外表面上的大气泡下方。在高热通量下，大气泡吸收一些从上游滑移来的气泡聚结成更大的细长团状变形气泡。考虑切向力平衡，液相速度和气相速度将由阻力和浮力的平衡决定。

${F_{\rm{d}}} = {F_{\rm{b}}}$

(15)

${F_{\rm{b}}} = \frac{{{\text π}D_{\rm{b}}^2}}{4}{L_{\rm{b}}}\left( {{\rho _{\rm{l}}} - {\rho _{\rm{g}}}} \right)g\sin \theta $

(16)

${F_{\rm{d}}} = \frac{{{C_{\rm{d}}}}}{2}{\rho _{\rm{l}}}{\left( {{u_{\rm{g}}} - {u_{\rm{l}}}} \right)^2} \cdot \frac{{{\text π}D_{\rm{b}}^2}}{4}$

(17)

式中： ${D_{\rm{b}}}$ 是蒸气层的厚度，m； ${C_{\rm{d}}}$ 是阻力系数； $\theta $ 是倾斜角。阻力系数 ${C_{\rm{d}}}$ 是 ${D_{\rm{b}}}$ 的函数^[18]，定义为

${C_{\rm{d}}} = \frac{2}{3}\frac{{{D_{\rm{b}}}}}{{{{\left[ {\displaystyle\frac{\sigma }{{g\left( {{\rho _{\rm{l}}} - {\rho _{\rm{g}}}} \right)}}} \right]}^{0.5}}}}$

(18)

联立式(15)—式(18)可得：

${u_{\rm{g}}} = {u_{{\rm{bl}}}} + {\left[ {\frac{{2{L_{\rm{b}}}\left( {{\rho _{\rm{l}}} - {\rho _{\rm{g}}}} \right)g\sin \theta }}{{{\rho _{\rm{l}}}{C_{\rm{d}}}}}} \right]^{0.5}}$

在单相紊流中，液相速度计算公式为^[19]

$ {u_{{\rm{bl}}}} = \frac{{0.758R{e^{ - 0.1}}G}}{{{\rho _{\rm{l}}}}}\left\{ {\ln \left[ {\frac{{0.152R{e^{ - 0.1}}G\left( {{\delta _{\rm{m}}} + \displaystyle\frac{{{D_{\rm{b}}}}}{2}} \right)}}{{{\mu _{\rm{l}}}}}} \right] - 0.61} \right\} $

式中： $R{\rm{e}}$ 为雷诺数，G为质量流速， ${\delta _{\rm{m}}}$ 为微液膜厚度， ${D_{\rm{b}}}$ 为气泡直径， ${\mu _{\rm{l}}}$ 为液相动力黏度。

实际过程是两相流动，使用经验常数0.758并不准确，因此气泡中心液相速度计算公式为

$ {u_{{\rm{bl}}}} = \frac{{CR{e^{ - 0.1}}G}}{{{\rho _l}}}\left\{ {\ln \left[ {\frac{{0.152R{e^{ - 0.1}}G\left( {{\delta _{\rm{m}}} + \displaystyle\frac{{{D_{\rm{b}}}}}{2}} \right)}}{{{\mu _{\rm{l}}}}}} \right] - 0.61} \right\} $

式中C是与半径有关的经验系数， $C = 0.15{R^2}$ 。

自然两相流动过程中，浮力是主要驱动力之一，沸腾产生的气泡拖曳周围的液相流动。因此，气泡层中心处的液相速度最高，气泡层内空泡份额较高，在气泡层内的液相速度可以认为等效于气泡中心处液相速度，然后向两边逐渐降低。由于大气泡紧挨宏液膜，宏液膜内的液相速度 ${u_{{\rm{lm}}}}$ 与气泡中心处液相速度 ${u_{{\rm{bl}}}}$ 呈正相关。

在流动沸腾的过程中，大气泡在加热的表面上形成，从壁上分离，然后再次形成，气泡的形状和大小会不断变化。为了便于计算，本文使用气泡的平均尺寸作为气泡的脱离直径，并且假设靠近壁的气泡的平均直径与气泡的分离直径相同，这样就可以获得流体力与气泡上的表面力之间的平衡关系。计算气泡直径采用Cole等^[20]推导出来的关系式：

${D_{\rm{b}}} = 1.5 \times {10^{ - 4}}{\left[ {\frac{\sigma }{{g\left( {{\rho _{\rm{l}}} - {\rho _{\rm{g}}}} \right)}}} \right]^{0.5}}{\left( {\frac{{{\rho _{\rm{l}}}{C_{{\rm{pl}}}}{T_{{\rm{sat}}}}}}{{{\rho _{\rm{g}}}{h_{{\rm{fg}}}}}}} \right)^{1.25}}$

式中： $\sigma $ 为表面张力， ${C_{{\rm{pl}}}}$ 为液相比热容， ${T_{{\rm{sat}}}}$ 为当地的饱和温度。

2 计算结果与分析 2.1 模型计算流程

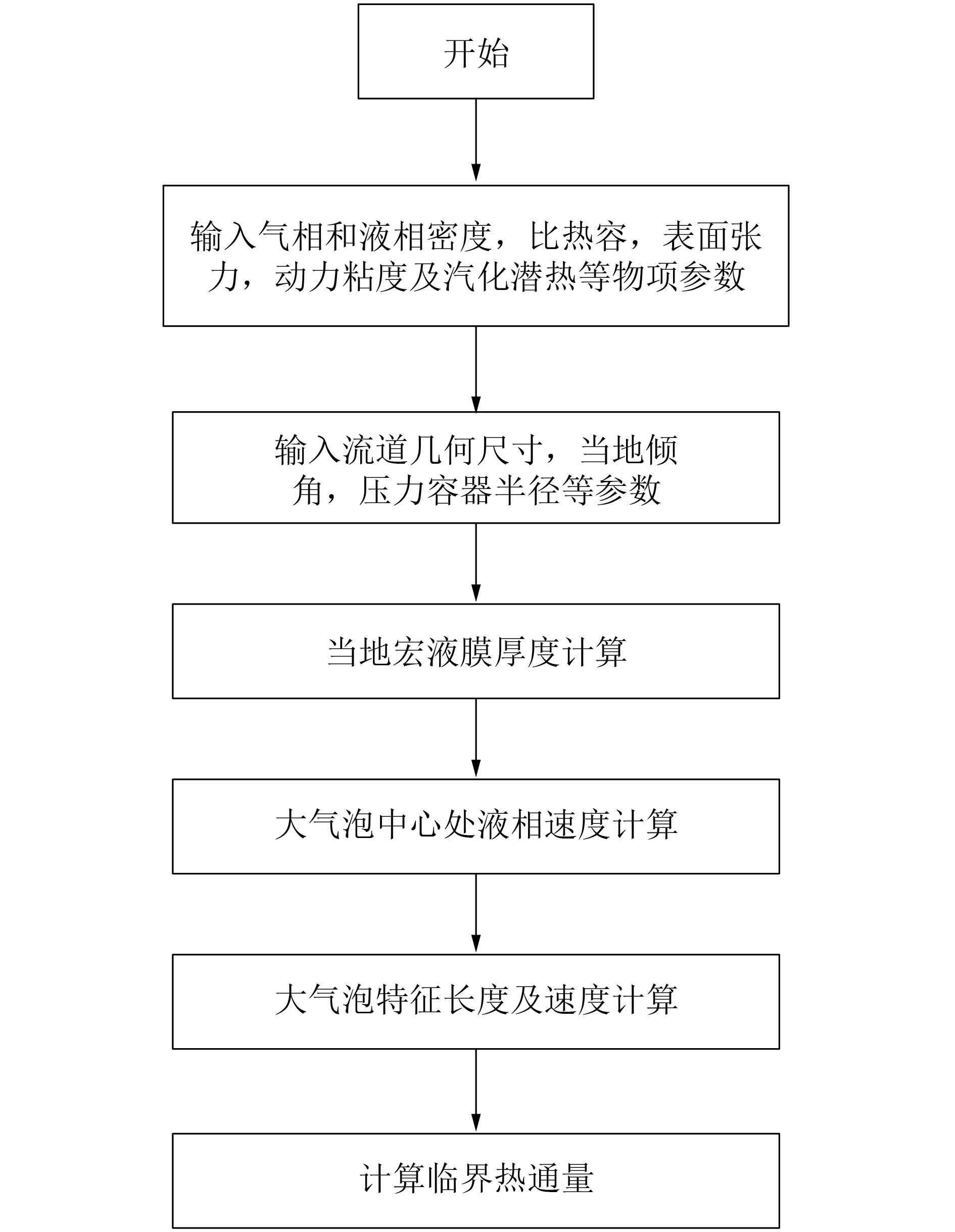
新建立CHF理论模型计算流程如图3所示。对于给定的管道尺寸、质量流量和入口水温，首先，计算微液膜的厚度；然后，通过质量守恒方程计算矩形通道内的气相速度和液相速度；最后，获得宏液膜蒸发带走的热量和单相及两相区过冷流体扩散入壁面带走的热量，两者相加可得当地的临界热流密度。

2.2 模型对比验证

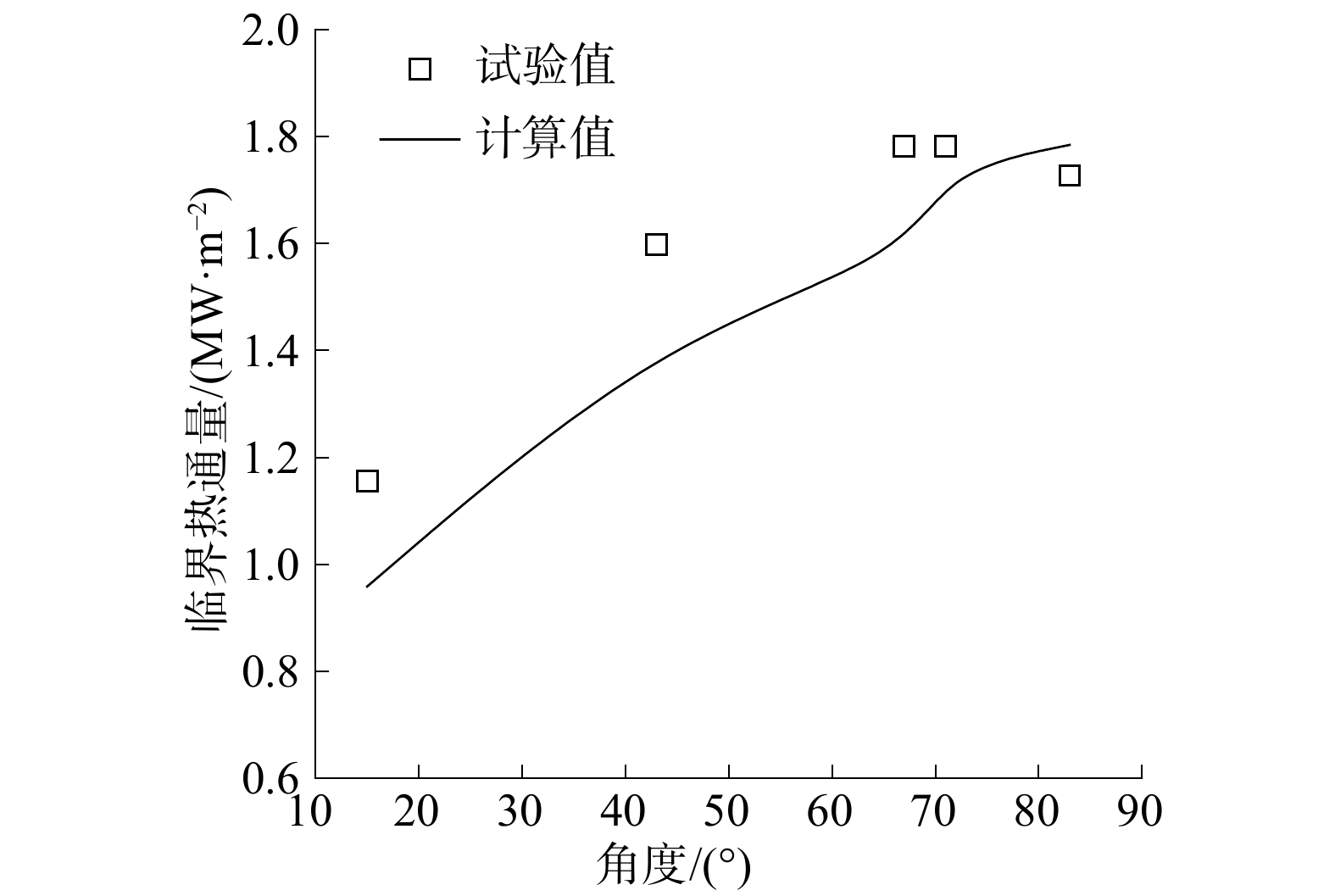
为验证本模型对CHF的预测效果，将模型预测结果和试验数据进行对比，本文采用Theofanous等^[21]有关ULPU-2400台架的试验数据。图4为不同角度计算值与试验值的比较。由图4可以看出，本文建立的CHF模型随角度的变化规律与实际试验相近，这说明建立的CHF模型对严重事故条件下压力容器外部的沸腾临界预测是有效的。

此外，由图4还可以看出，CHF值随着角度的增加先是增加较快，到达一定角度(65°~70°)后，变化开始趋于平缓，甚至略有下降。这一方面是由于气泡上游的累积效应造成壁面传递到两相边界层和单相区的热量减少；另一方面，随着倾角的增加，气相速度有所增加，同一时间段内带走的热量增多。CHF最终的变化趋势是由上述2种因素综合作用的结果。

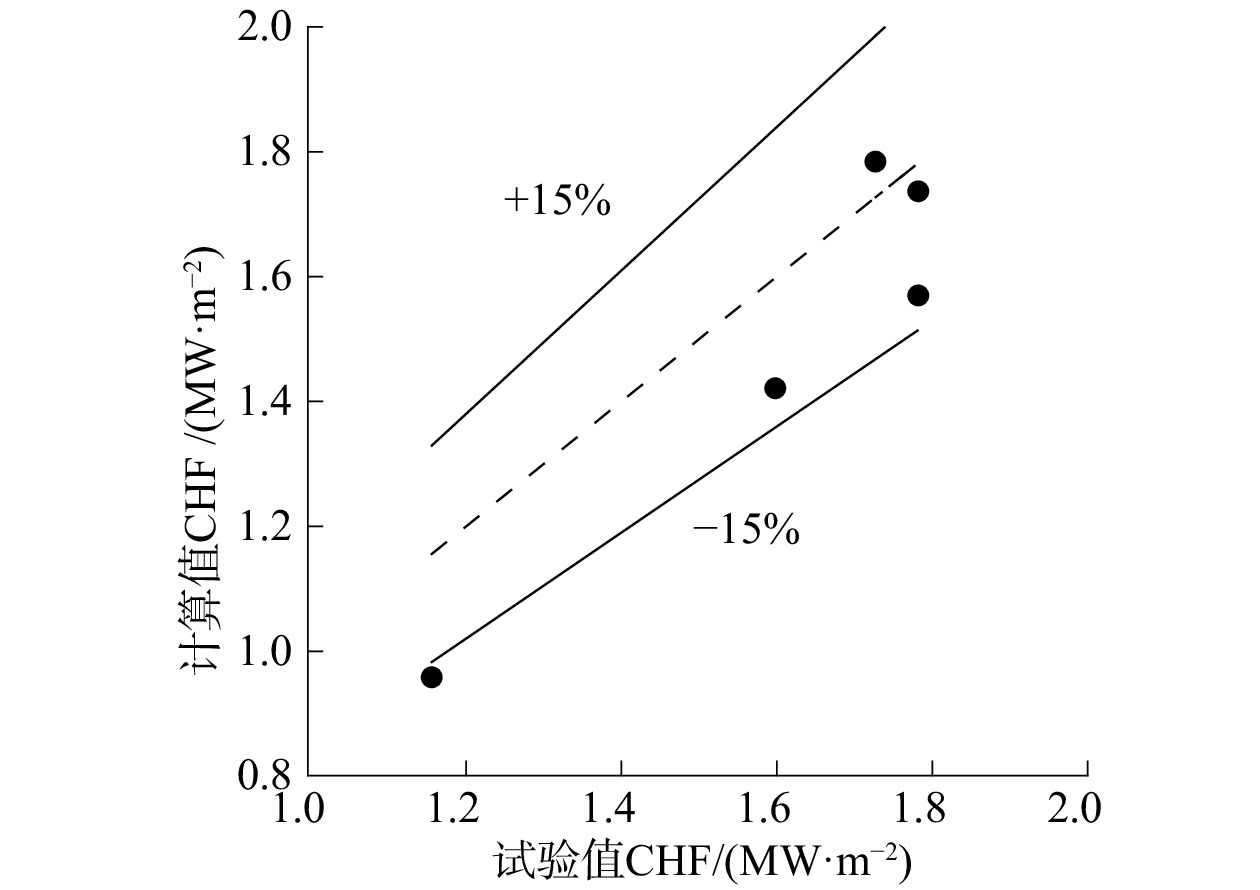
由图5可以看出，本模型与试验数据的计算精度在15%以内，模型计算结果与试验数据的一致性较高，并能较准确地预测CHF变化趋势。

2.3 影响因素分析

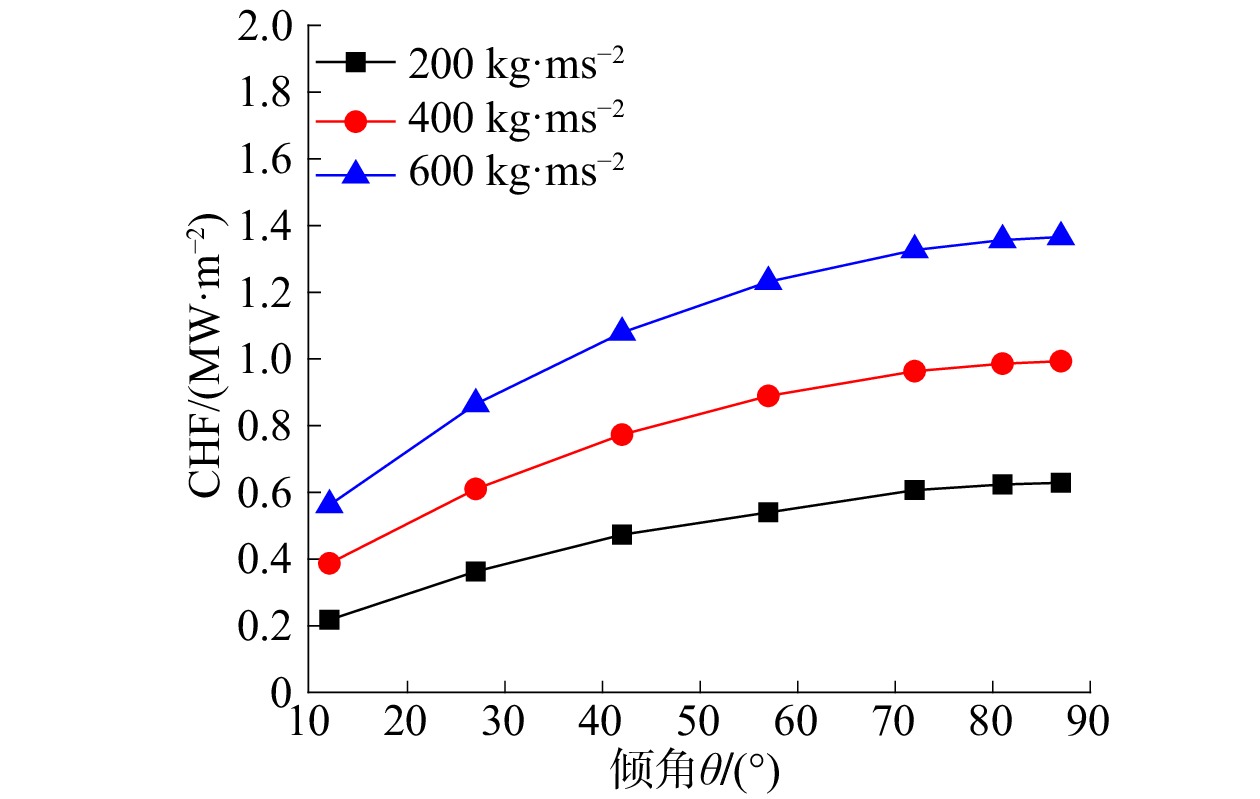
图6为流道深度0.15 m、压力容器半径2 m时，不同质量流速对CHF的影响。由图6可以看到，质量流速的增加对可以显著提升CHF。

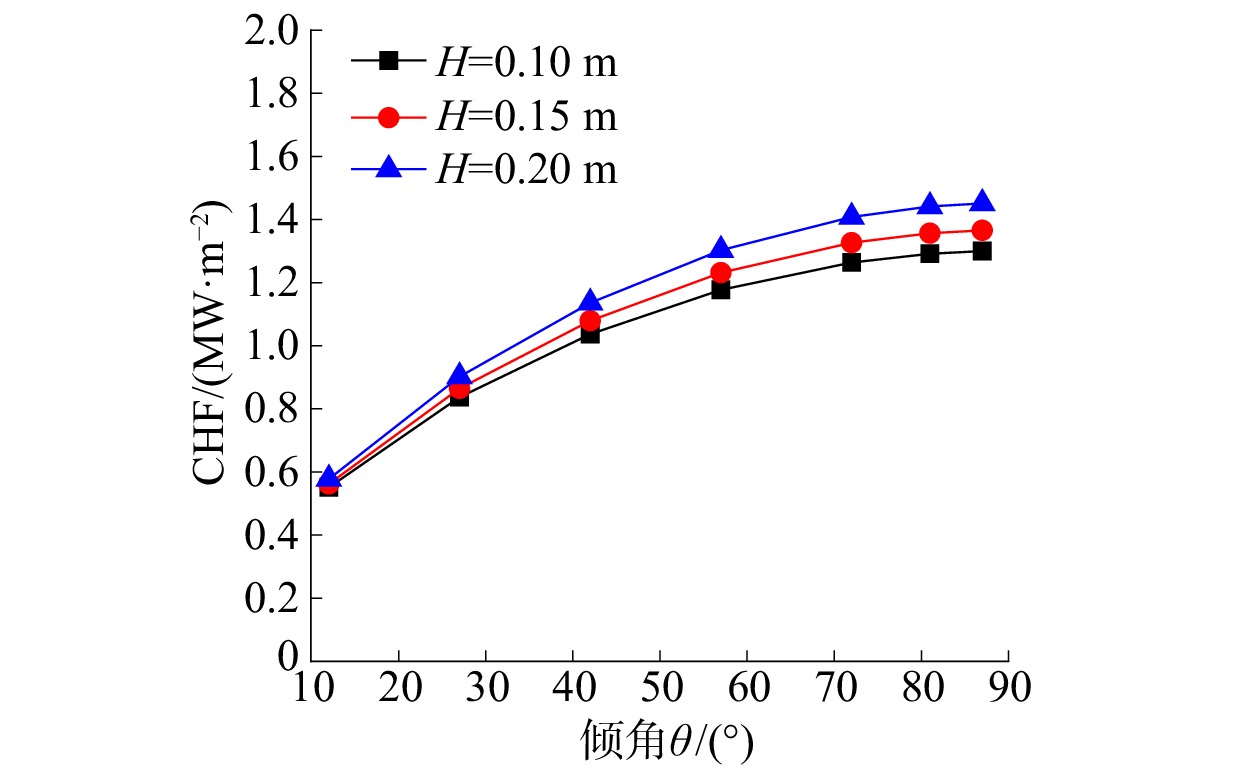
图7为压力容器半径2 m、质量流速600 时，不同流道深度对CHF的影响。由图7可以看出：1)在质量流速一定的情况下，适当增加流道深度(0.01 m)可以提升CHF，但CHF提升幅度相比质量流速的影响要小。2)流道深度的变化对小角度CHF影响稍小，对大角度CHF的影响稍大。这是因为气泡受浮升力与阻力的共同作用，小角度气相流速相对大角度较小，大角度通过相变带走的热量更多。

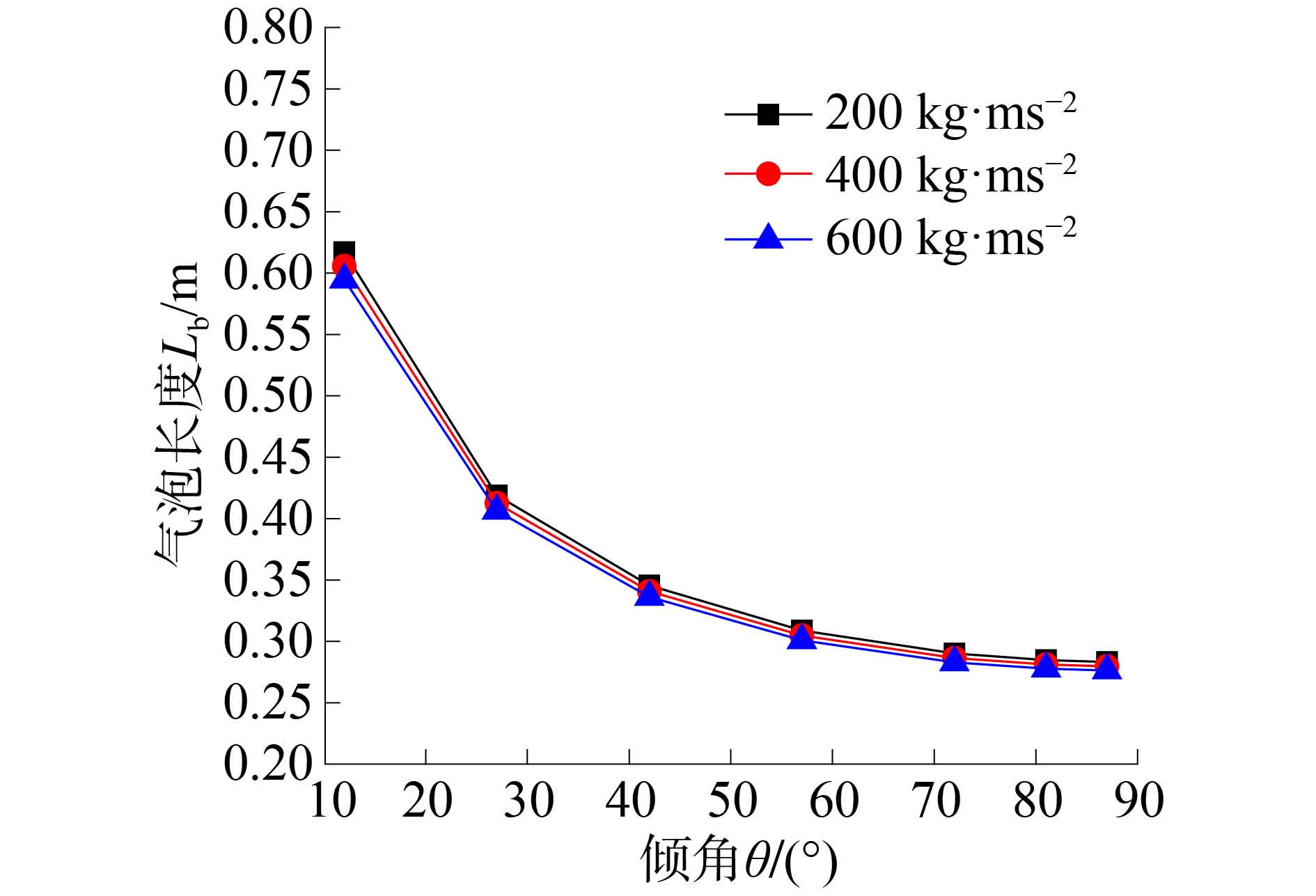
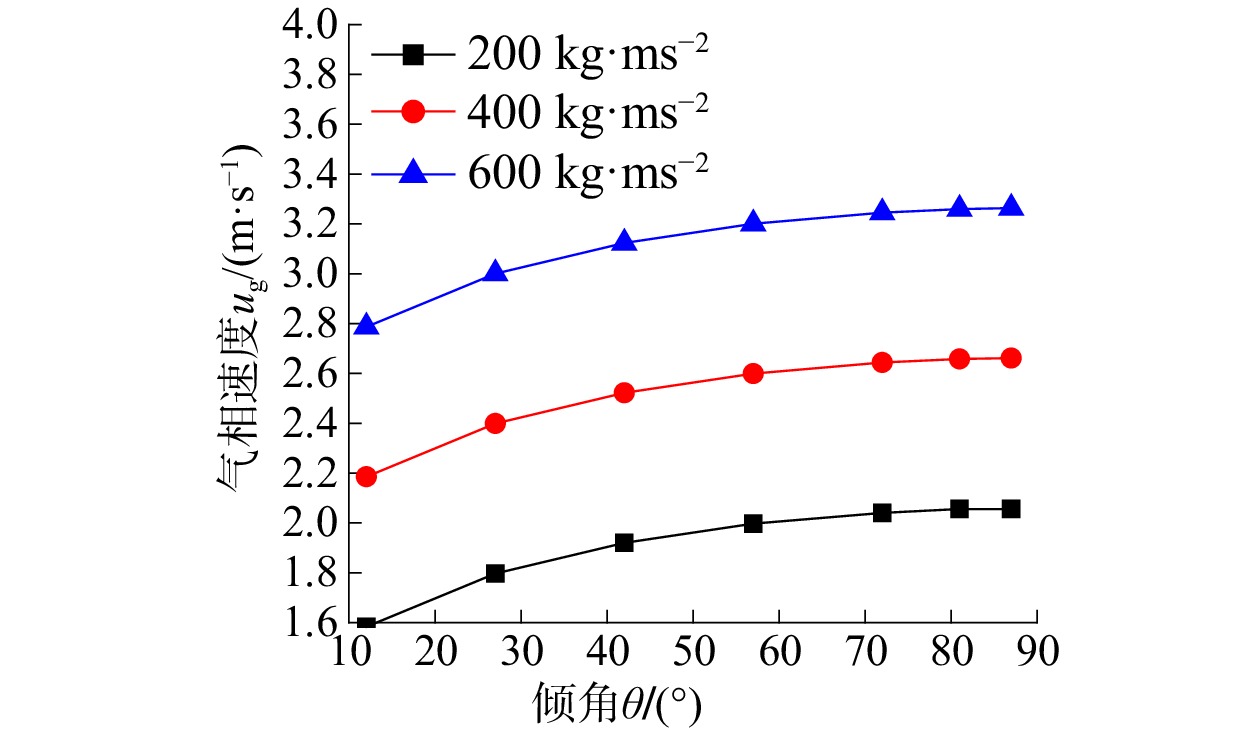
图8和图9选取的是压力容器半径为2 m、流道深度为0.15 m条件下的数据。由图8和图9可以看出：质量流速低时，气泡的尺寸较大，气相的速度也较低；相同质量流速时，气泡的尺寸随着倾角的增加而变短；气泡的尺寸随着质量流速的增加而减小；气相的速度则随着质量流速的增加或倾角的增加而增大。

3 结论

本文在分析现有试验数据的基础上，基于水动力不稳定性模型及宏液膜理论，建立了适用于严重事故条件下压力容器外部CHF理论模型。

1)对于不同区域，必须考虑空泡份额分布的影响，不同区域平均空泡份额在0.013~0.915变化，进而求解出两相边界层厚度。

2)单相紊流中液相速度的求解大体上可应用于两相流动，但直接应用会造成较大的误差，相关的经验系数需要进行修正。

3)对严重事故条件下压力容器外部的CHF进行了计算。发现其他条件相同时，质量流速、倾角和流道深度的增加均对CHF产生有益的影响。

将计算结果与Dinh等的试验数据进行了对比分析。结果表明，模型计算结果与实际试验数据误差在15%以内，符合较好。该模型对改善IVR-ERVC流道结构设计及CHF理论研究都有一定借鉴意义。