2. 哈尔滨工程大学 航天与建筑工程学院,黑龙江 哈尔滨 150001
2. College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, China
铁素体钢材是目前生产生活中最常用的钢材料之一,在钢材料及结构的服役期间,通常会发生一系列的断裂问题,从而造成不可估量的损失。断裂韧性是评估材料或结构完整性的重要指标之一。对于材料的断裂破坏分析,通常有两大判据指标,即冲击韧性指标(冲击吸收功)和断裂韧性指标(应力强度因子K、J积分临界值或裂纹尖端张开位移值)。其中,断裂韧性指标虽然可直接用于结构完整性评定,比冲击吸收功更合理安全[1],但断裂韧性试验方法复杂、成本高、费时费力,有时甚至难以进行。而冲击韧性试验方法原理简单,对材料的宏观缺陷、显微组织变化都很敏感,可揭示和反映材料的脆断倾向和程度。夏比冲击试验因其设备简单、试验时间短和试件加工简单等优点,常常作为测量冲击韧性的方法,在实际生产中得到了广泛的应用。孔祥伟等[2]通过对Q390钢进行夏比冲击试验,并利用主曲线法求得了Q390钢韧脆转变区内冲击吸收功的类主曲线分布模型。该模型表示冲击吸收功以失效概率为50%的曲线为中心,离散性地分布在5%~95%的上下边界之间。黄飞等[3]利用仪器化夏比冲击试验机进行夏比冲击试验,测的Q420q桥梁钢不同温度下冲击吸收能量和冲击试样断口纤维断面率,以断口形貌的剪切断面率为50%所对应的温度作为桥梁钢的韧脆转变温度。Barsom等[4]在对各类强度钢材进行分析整理后,得到了不同区域的转化公式,并提出了韧脆转变区转化的2种方法。Coates等[5]在前人的基础上,对相应转化公式进一步细化,分别总结出上平台、韧脆转化区和下平台的转换关系式,但是对于不同类型的钢材需用到不同的经验公式,对于一些特种用钢及新型钢材的转换则需要进一步探讨。
目前国内外对于铁素体钢材断裂韧性的测试方法种类繁多,而并未对铁素体钢材断裂韧性测试进行具体规定。本文采用夏比冲击试验方法对铁素体钢材典型材料Q345B钢的断裂韧性进行研究,利用经验法和主曲线法得到了材料断裂韧性曲线,通过对比有限元模拟结果与已有的实验结果,验证了有限元模拟方法的可行性,为后续研究提供参考。
1 研究方法 1.1 经验公式法对于夏比冲击试验来说,同一试件在相同约束条件及不同温度下进行试验测定的夏比冲击吸收功会有很大不同,因此利用夏比冲击吸收功预测断裂韧性需划分为不同阶段,分别称为上平台区、韧脆转变区及下平台区。上平台区位于温度相对较高的区域,曲线的形状相对平缓,夏比冲击吸收功的数值相较于下平台区及韧脆转变区来说相对较高。下平台区位于温度较低的区域,曲线形状相对也较为平缓,夏比冲击吸收功的数值相较于下平台区及韧脆转变区来说相对较低。在上、下平台区之间,便是韧脆转变区,该部分曲线相对陡峭,在相对短的温度区间内,夏比冲击吸收功的数值会有一个相对大的提升,曲线更为陡峭。在对3个不同区域进行转化的时候,需要用到不同的转化方程,而对于不同的材料而言,在相同区域内所用到的转化方程也不相同[6]。
1.2 主曲线法主曲线法是以统计学中经常采用的弱链统计方法为基础,经过适用性分析之后提出的三参数Weibull模型,通过该模型将断裂韧性与失效概率之间建立特性的线性关系。该模型利用分布函数的方式,解决了在韧脆转变区中断裂韧性分布离散性较大的问题[7-10],具体公式为
| ${P_{\rm{f}}} = 1 - \exp \left[ { - \frac{B}{{{B_0}}}{{\left( {\frac{{{K_{\rm{JC}}} - {K_{\min }}}}{{{K_0} - {K_{\min }}}}} \right)}^4}} \right]$ |
式中:
人们在研究中逐渐发现由铁素体钢材结合主曲线法得到的材料韧脆转变区的曲线形状基本相同。根据ASTM标准中对于大量压力容器材料实验中的总结,将夏比冲击标准试件在50%失效概率下的曲线定义为主曲线,如式(1)所示[8]:
| ${K_{{\rm{JC}}({\rm{med}})}} = 30 + 70\exp \left[ {0.019(T - {T_0})} \right]$ | (1) |
式中T0为参考温度中值断裂韧性值,即断裂韧性数值为100时所对应的试验温度。
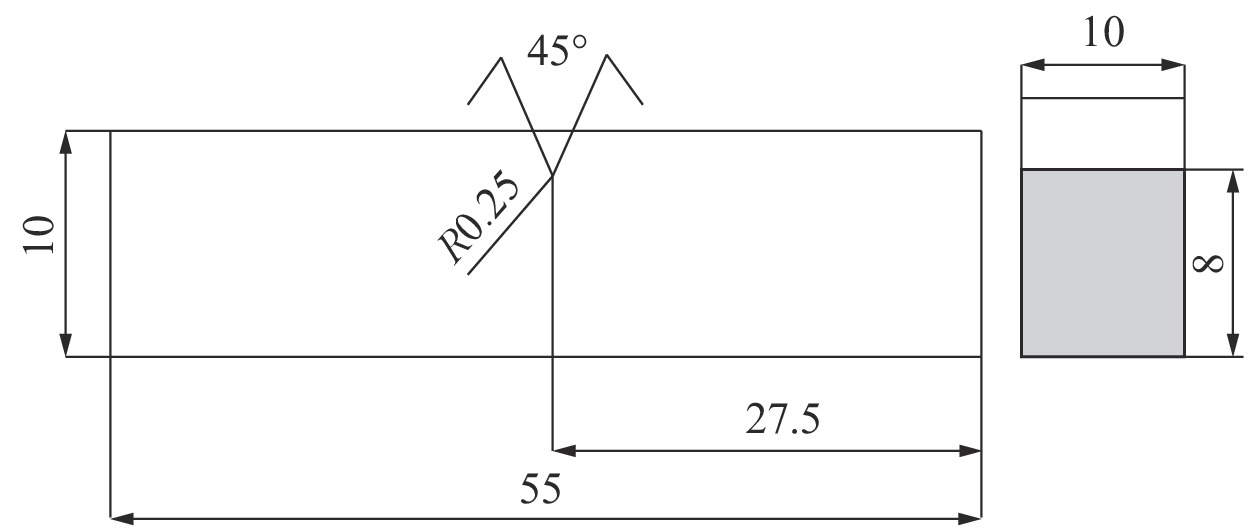
2 断裂韧性求解 2.1 建立模型本次模拟采用夏比冲击标准尺寸试件进行,试件长度L取值55 mm,宽度B取值10 mm,高度W取值10 mm,中间部位设置深度2 mm、开口角度45°的V型缺口,加载及支撑装置简化处理,采用2 mm冲击刃,支座间隔距离取值40 mm,几何尺寸示意如图1所示。
|
Download:
|
| 图 1 夏比冲击试件尺寸 | |
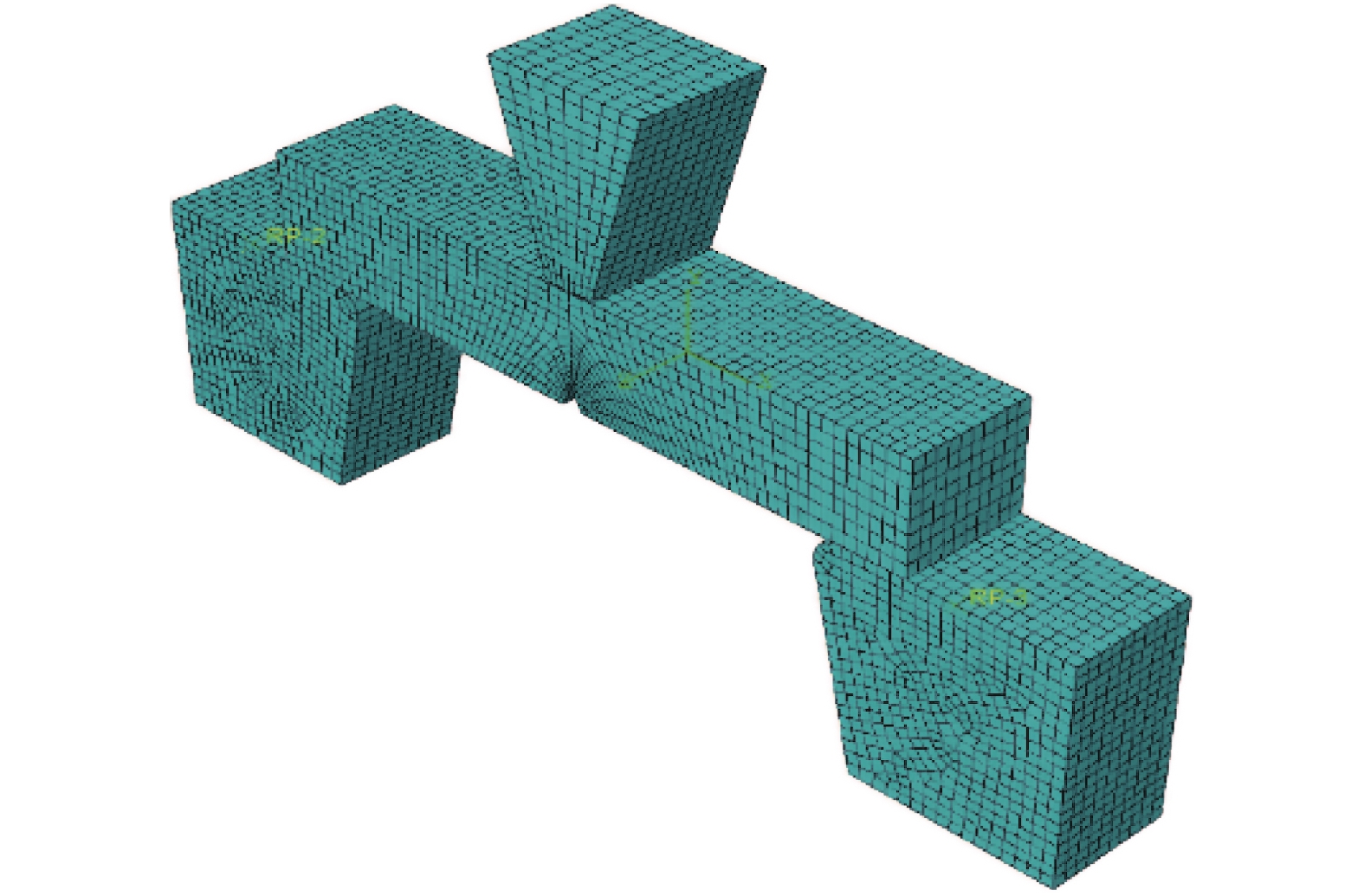
试件材料采用Q345B钢材,根据材料拉伸试验的结果,将材料屈服强度取值为372.6 MPa,弹性模量取值206 GPa,泊松比取值0.3,材料应变硬化指数取值0.4,切向摩擦系数取0.2[7]。网格采用四面体网格,网格划分时对裂纹尖端进行奇异单元处理,从而对材料的断裂进行更为细致的计算,夏比冲击标准试件单元总数为6 220个,划分网格后模型如图2所示。
|
Download:
|
| 图 2 模型网格 | |
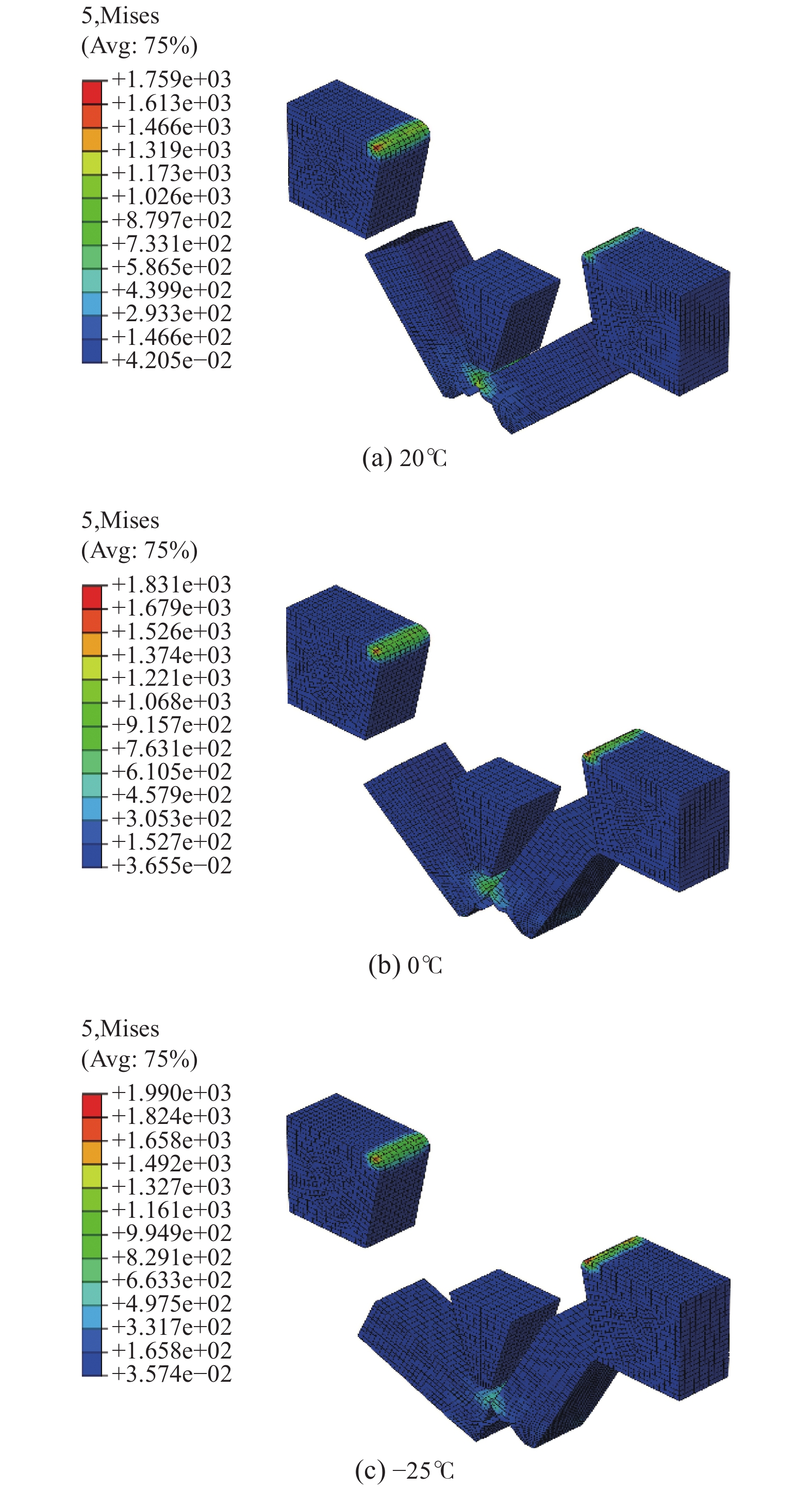
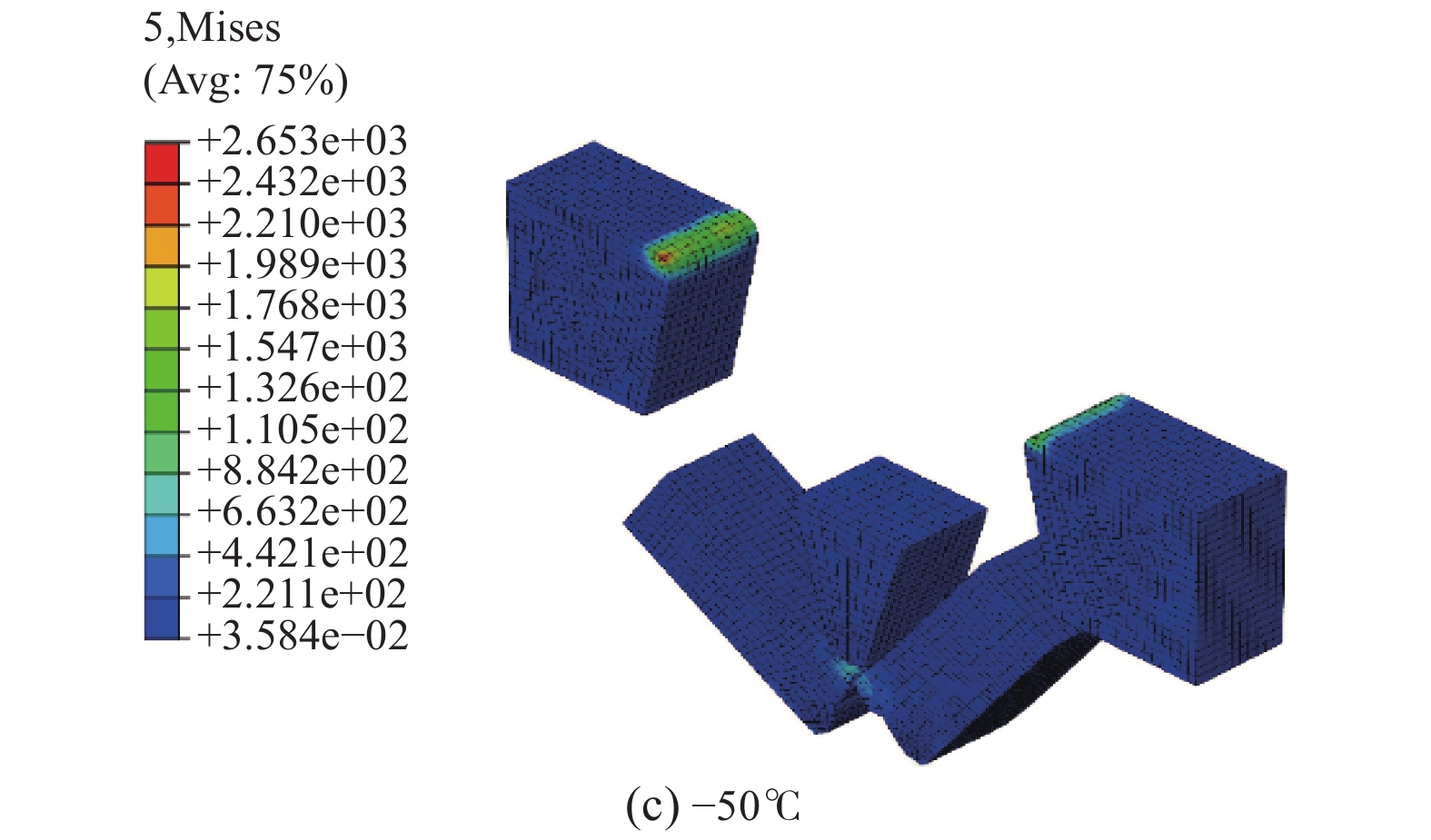
对2个支撑底座及冲击刃进行约束,支撑底座固定自由度且冲击刃只能沿竖直方向运动,摩擦系数取0.2。设置能量为输出变量,对150 J摆锤试验机进行模拟。由于本次研究模拟温度环境分别为20、0、−25、−50 ℃,所以需对初始温度场分别进行设定。各温度下模拟结果应力如图3所示。
|
Download:
|
| 图 3 | |
|
Download:
|
| 图 3 不同温度夏比冲击模拟示意 | |
由图3应力云图能够清晰地看出,随着设定试验温度的降低,在试件发生断裂过程中吸收的能量逐渐降低,整理得到部分夏比冲击吸收功与模拟温度如表1所示。
|
|
表 1 夏比冲击吸收功模拟值 |
|
|
表 2 夏比冲击吸收功试验值 |
由实验结果及整理所得数据可以看出,随着温度的降低,试件的夏比冲击吸收功呈逐渐降低趋势,从而判断出相同试件在同样的荷载下发生断裂时所需要的外部能量较小,则相应的抵抗断裂的能力较弱,进而对应的断裂韧性值相对较小。通过对比有限元模拟的吸收功结果,发现模拟与实验误差在10%以内,验证了模拟方法的可行性,为进一步研究提供了基础。
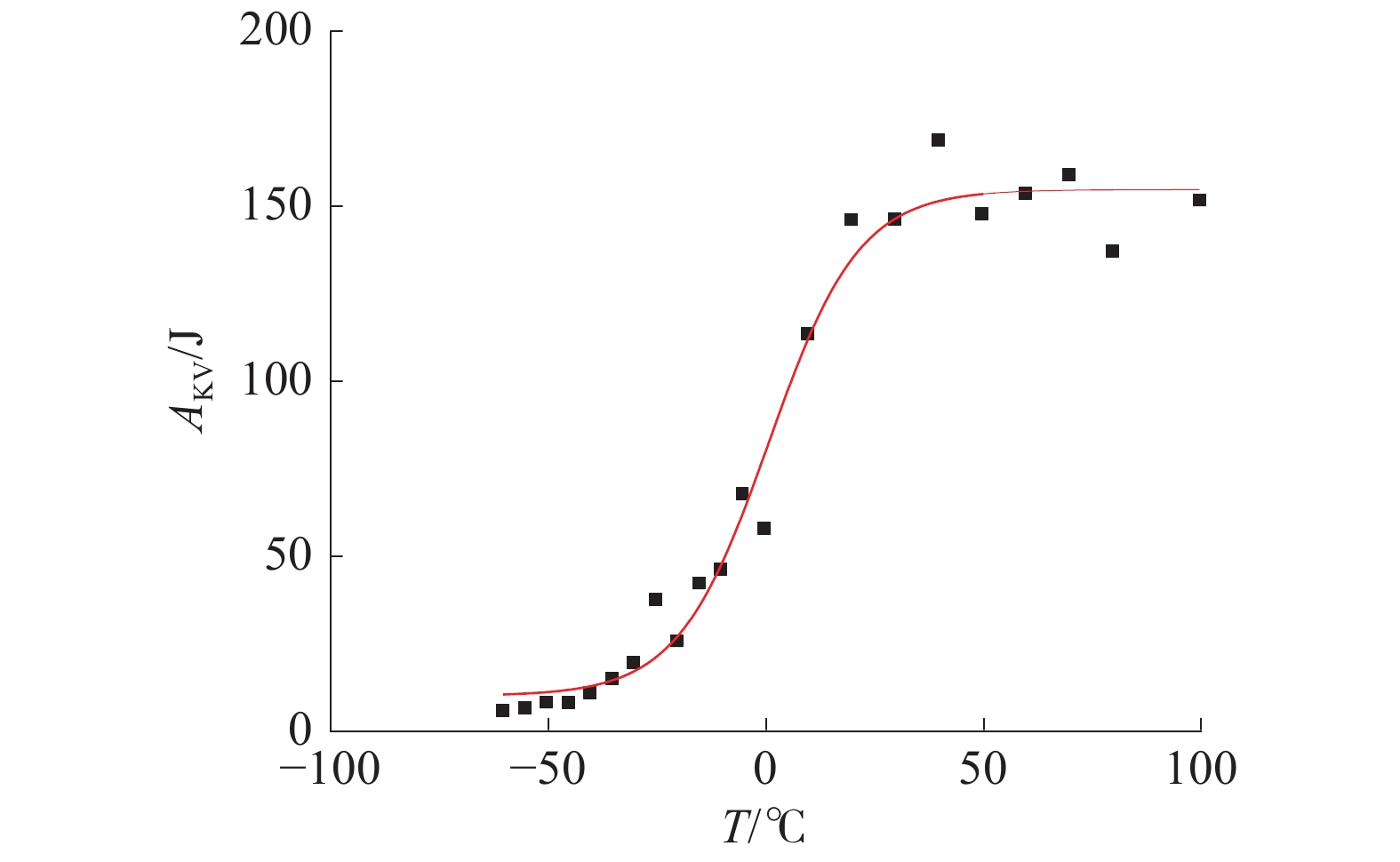
2.3 断裂韧性计算采用玻尔兹曼函数[12]对表2夏比冲击吸收功进行拟合,得到夏比冲击吸收功与温度的拟合关系如式(2)所示,拟合曲线如图4所示。
|
Download:
|
| 图 4 吸收功拟合曲线 | |
| ${A_{\rm{KV}}} = \frac{{ - 144.75}}{{1 + {{\rm{e}}^{\frac{{T - 1.46}}{{2.33}}}}}} + 154.75$ | (2) |
式中:
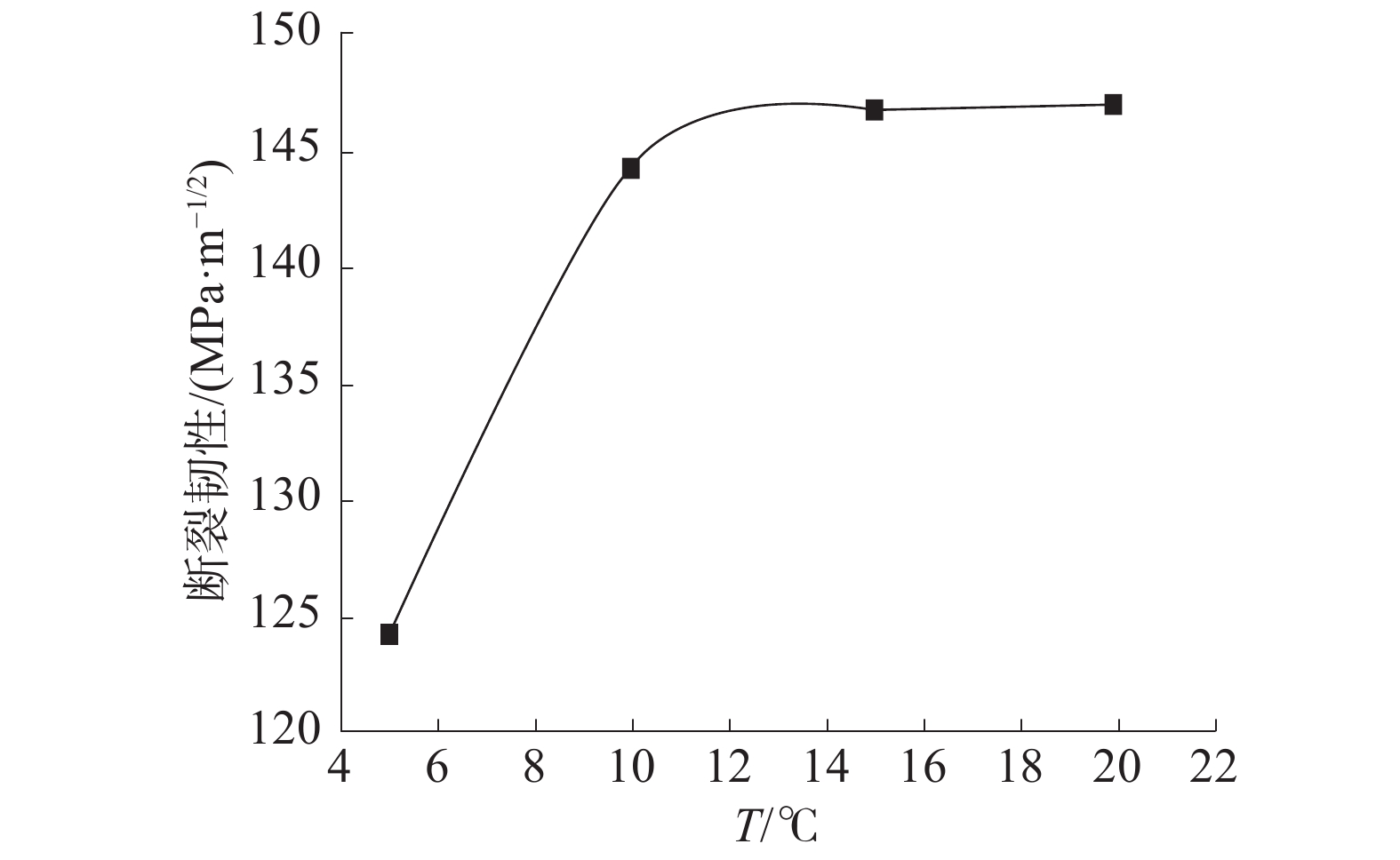
由前文分析可知,在使用经验公式法对断裂韧性曲线进行求解时,需要将曲线划分为上平台区、韧脆转变区和下平台区。结合已有的实验数据[13]首先进行上平台区的转化,利用经验公式法对夏比冲击吸收功进行转化,得到上平台区曲线如图5所示。由上平台曲线可以看出,温度在5~10 ℃时,断裂韧性值有一个较大的提升,温度超过10 ℃之后,断裂韧性值继续上升,但增大的速率明显降低。
|
Download:
|
| 图 5 上平台区断裂韧性曲线 | |
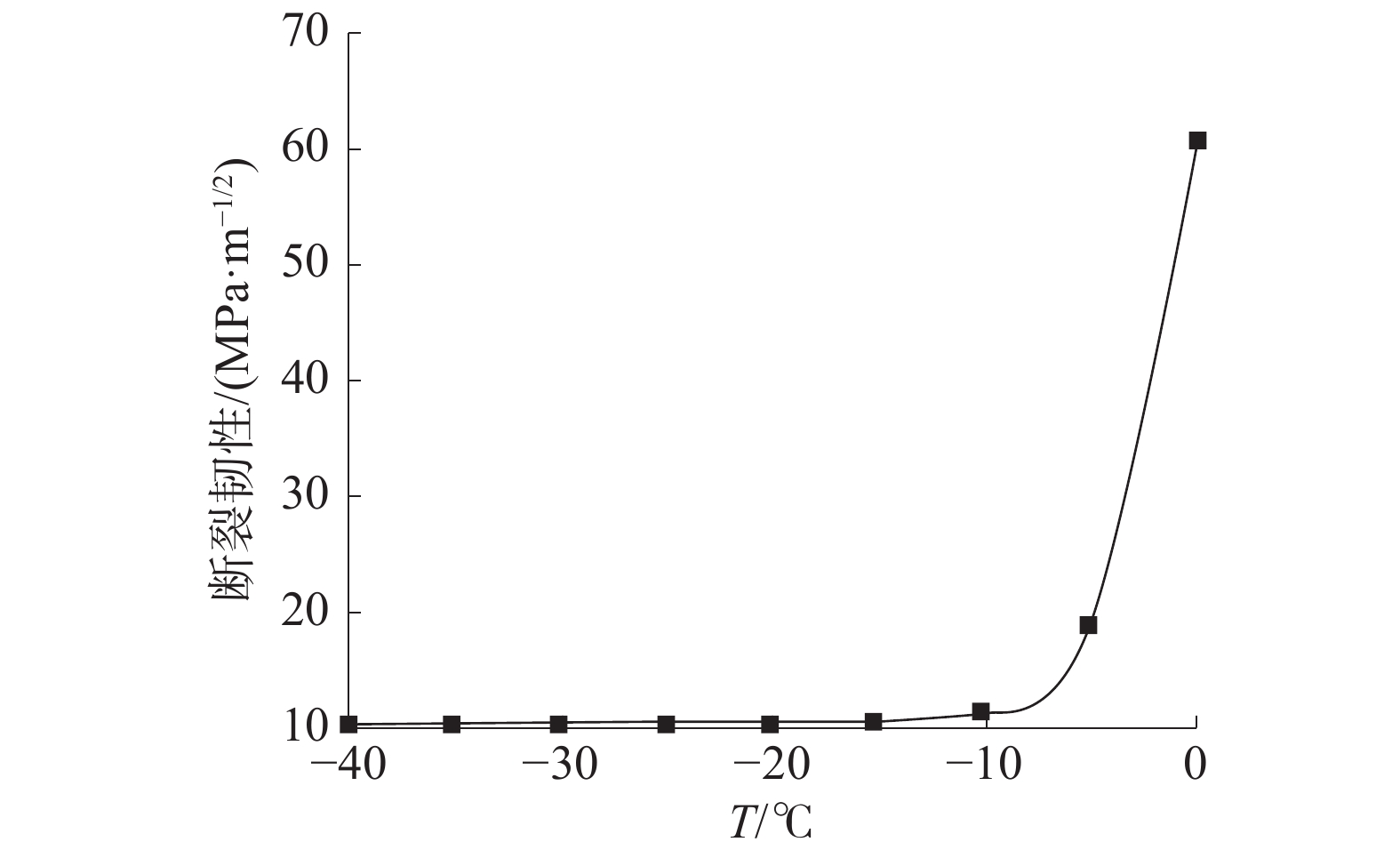
接着利用经验公式法对材料韧脆转变区及下平台的断裂韧性进行转化,将0 ℃及以下的相应数据带入经验法计算中,采用“一步法”进行计算,得到韧脆转变区及下平台曲线如图6所示。由图6可以看到,在温度大于−10 ℃时,断裂韧性值上升速率极大;而在小于−10 ℃时,断裂韧性值虽有上升趋势,但曲线比较平直。
|
Download:
|
| 图 6 韧脆转变区及下平台区断裂韧性曲线 | |
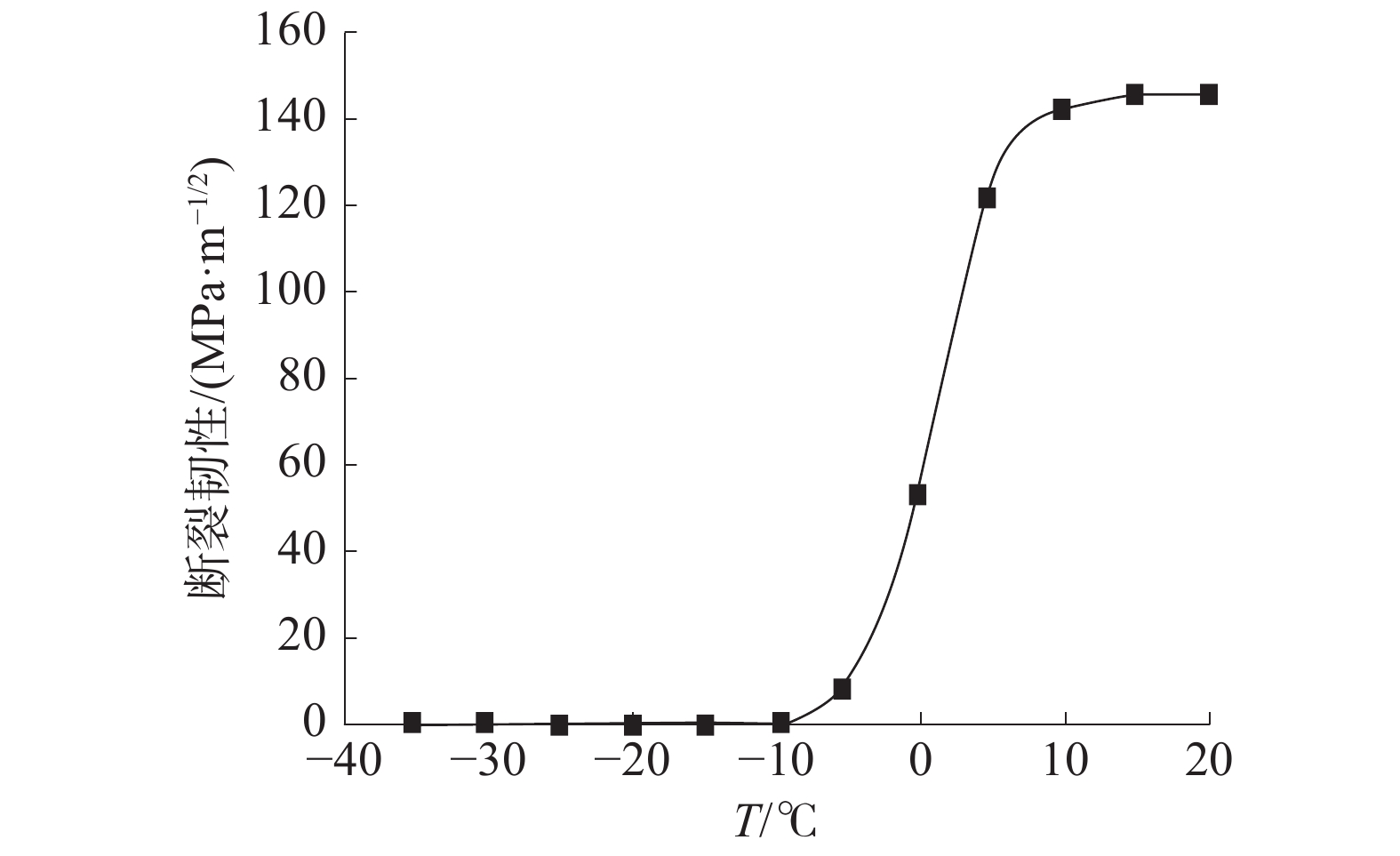
将上平台区、韧脆转变区及下平台区曲线拟合,得到断裂韧性曲线如图7所示。可以看到,由夏比冲击吸收功预测得到的断裂韧性曲线中,能够清晰地反映断裂韧性随温度变换而产生的变化,且上平台、韧脆转变区、下平台之间的位置较为明显。试验结果能够较为准确地反映Q345B钢材的断裂韧性,同时对钢材在不同温度条件下的应用提供了良好的技术基础。
|
Download:
|
| 图 7 经验公式法断裂韧性曲线 | |
在用经验公式法求解断裂韧性曲线时,需要分3段进行处理,过程较为复杂,且3段曲线进行拟合的时候,更容易产生误差。而主曲线法只需根据参考温度T0一个参量便可以详细地描述出断裂韧性曲线,运算过程更加简便且能更好地减小相应的误差。通过由玻尔兹曼函数拟合而成的夏比冲击吸收功随温度变化的曲线,分别对28 J和41 J夏比冲击吸收功所对应的试验温度计算得到参考温度T0,求得T28 J=−3 ℃,T41 J=−1.57 ℃。选用28 J的对应的温度参数进行断裂韧性预测参数(IGC参数)的计算,求解IGC参数PIGC(28 J)=−3.1,PIGC(41 J)=−1.6。
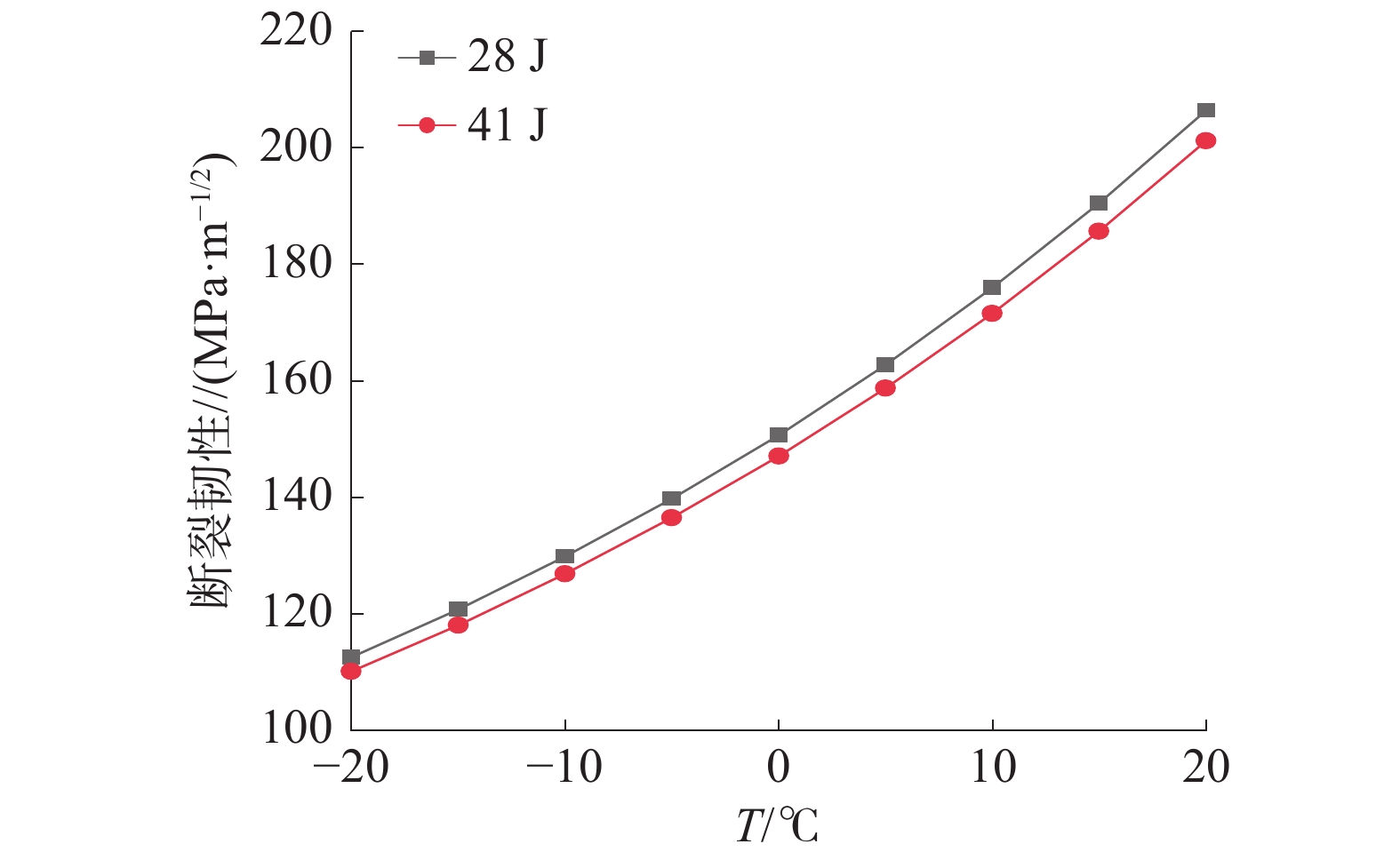
根据主曲线法可求得参考温度T0,28 J=−28.7 ℃,T0,41 J=−27.1 ℃,使用单温度法将求得的参考温度带入式(1)可得曲线方程如式(3)和式(4)所示,方程曲线如图8所示。
| ${K_{\rm{JC}}} = 30 + 70\exp \left[ {0.019\left( {T + 28.7} \right)} \right]$ | (3) |
| ${K_{\rm{JC}}} = 30 + 70\exp \left[ {0.019\left( {T + 27.1} \right)} \right]$ | (4) |
|
Download:
|
| 图 8 韧脆转变区断裂韧性曲线 | |
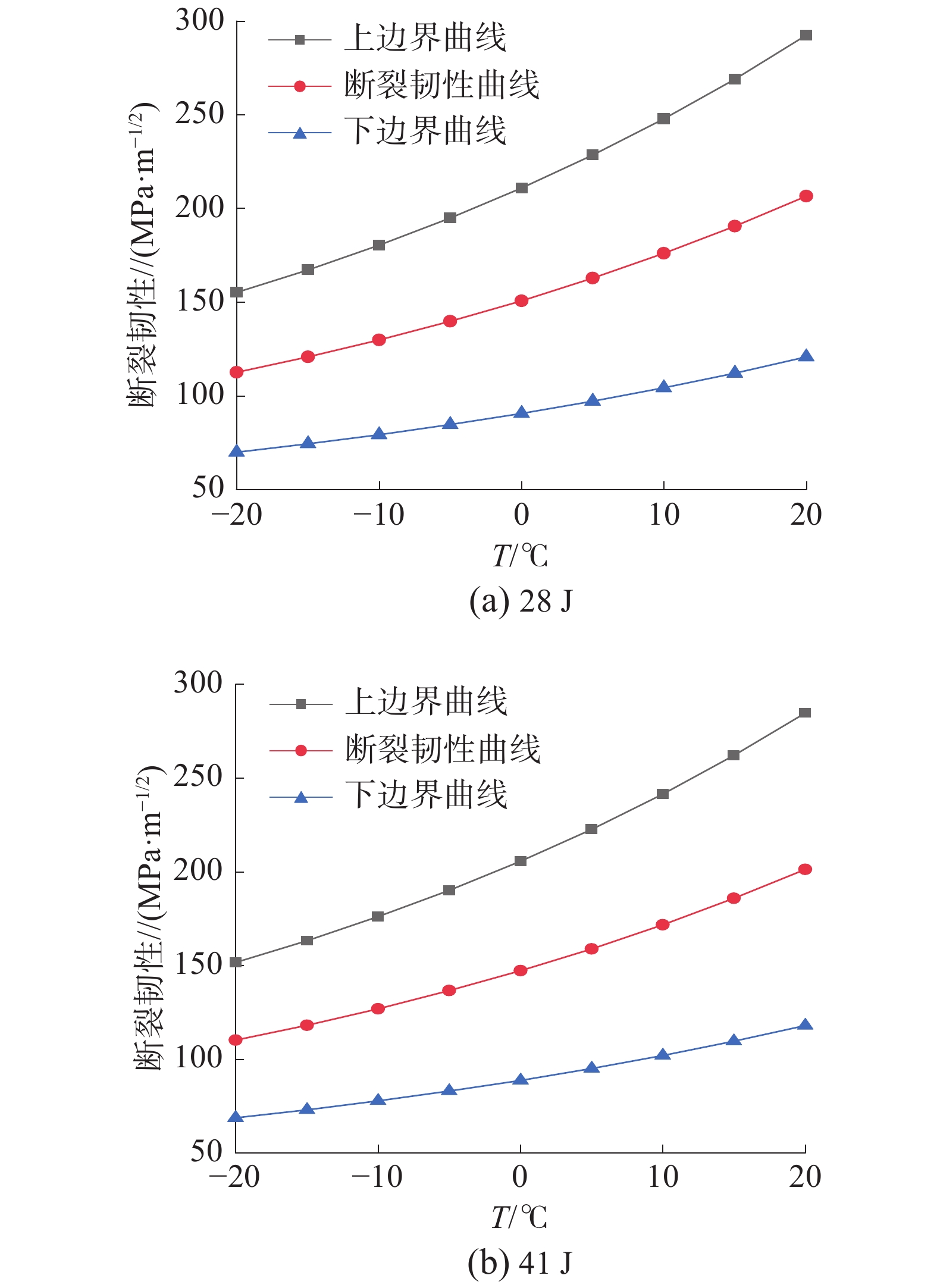
上下边界方程曲线如图9所示。其中:28 J上、下边界曲线分别如式(5)和式(6)所示;41 J上、下边界曲线分别如式(7)和式(8)所示。
|
Download:
|
| 图 9 断裂韧性曲线 | |
| ${K_{\rm{JC}\left( {5\% } \right)}} = 25.4 + 37.8\exp \left[ {0.019\left( {T + 28.7} \right)} \right]$ | (5) |
| ${K_{\rm{JC}\left( {95\% } \right)}} = 34.6 + 102.2\exp \left[ {0.019\left( {T + 28.7} \right)} \right]$ | (6) |
| ${K_{\rm{JC}\left( {5\% } \right)}} = 25.4 + 37.8\exp \left[ {0.019\left( {T + 27.1} \right)} \right]$ | (7) |
| ${K_{\rm{JC}\left( {95\% } \right)}} = 34.6 + 102.2\exp \left[ {0.019\left( {T + 27.1} \right)} \right]$ | (8) |
由图8可以看出,通过28 J和41 J吸收功相关参数计算所得断裂韧性曲线结果相差不大,且曲线的上升情况基本一致,通过不同的方法得到的断裂韧性曲线基本符合相应要求。通过分析图9可以发现,断裂韧性曲线位于上边界曲线及下边界曲线包络处,符合设计预期。
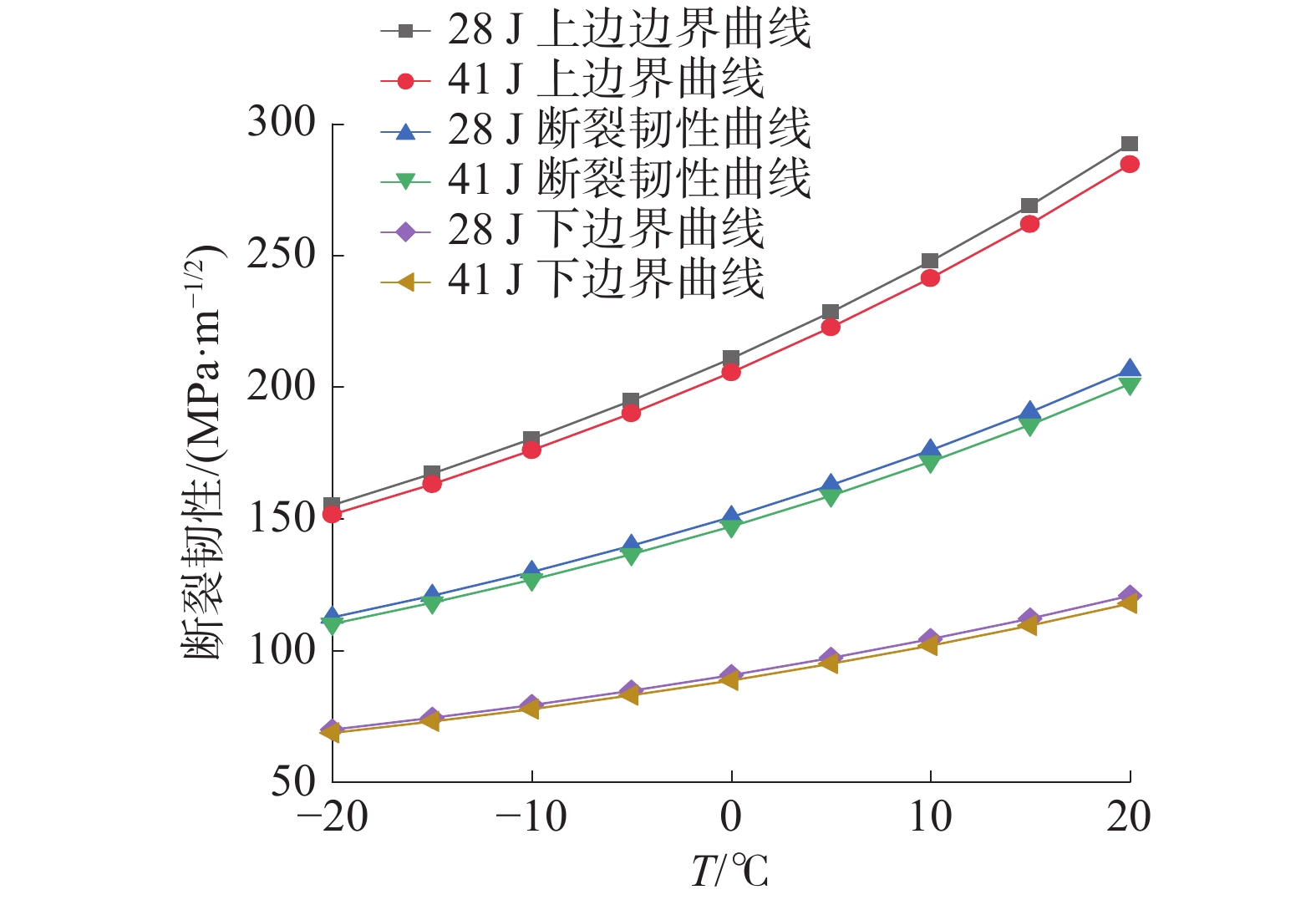
将28 J及41 J的上边界曲线、断裂韧性曲线及下边界曲线汇总,最终形成图10。由图10中各项数据可知,基于2种不同能量所得曲线,无论是上边界、下边界还是断裂韧性曲线,差距均不大,都可以准确地描述相应区间内材料、试件的断裂韧性值。相较于经验公式法,主曲线法能更为简便地通过不同参数得到基本相同的断裂韧性曲线。
|
Download:
|
| 图 10 断裂韧性曲线汇总 | |
本研究主要通过Q345钢夏比冲击吸收功测定了材料断裂韧性曲线,主要结论如下。
1)介绍了夏比冲击吸收功转化为断裂韧性曲线的2种基本方法,即经验公式法和主曲线法。由于经验公式法需要根据不同平台进行不同转化公式的选择,因此进行了不同区间内转化公式的分析,最终确定需要用到的相应公式。同时对主曲线法进行了详细介绍,最终给定主曲线法的判定方程。
2)对夏比冲击试验进行数值模拟,分别得到0、200 ℃时材料的夏比冲击吸收功,将所得数据与前人数据进行归纳总结,可知误差均在10%以内。
3)利用经验公式法中所总结的3段平台区域转化公式对断裂韧性曲线进行计算,得到断裂韧性随温度变化的曲线,所得试验结果与预测值相符。
4)利用主曲线法转化方程,根据28 J及41 J吸收功的相应参数,得到主曲线法所需参考温度,带入主曲线法相应方程,分别得到与之对应的参考温度,结果表明,二者所求的断裂韧性曲线基本重合,相应数据基本准确,所得数据能够反映材料的基本力学性能。
| [1] |
张新平, 史耀武. 用Charpy试样研究核压力容器钢的韧性转变温度曲线[J]. 核动力工程, 1995, 16(2): 166-170. ( 0) 0)
|
| [2] |
孔祥伟, 李绪清, 兰亮云, 等. Q390钢韧脆转变区冲击吸收功的类主曲线模型[J]. 东北大学学报(自然科学版), 2018, 39(5): 663-667. DOI:10.12068/j.issn.1005-3026.2018.05.012 ( 0) 0)
|
| [3] |
黄飞, 朱兴江, 张久峰, 等. Q420q桥梁钢动态断裂韧性的研究[J]. 现代冶金, 2018, 46(1): 11-13. DOI:10.3969/j.issn.1005-6068.2018.01.003 ( 0) 0)
|
| [4] |
BARSOM J M, ROLFE S T. Kic Transition-temperature behavior of A517-F Steel
[J]. Engineering fracture mechanics, 1971, 2(4): 349-357. ( 0) 0)
|
| [5] |
COATES M, KUMAR A, ROBERTS S G. Crack initiation in the brittle fracture of ferritic steels[J]. Fatigue & fracture of engineering materials & structures, 2006, 29(9/10): 661-671. ( 0) 0)
|
| [6] |
BARSOM J M, ROLFE S T. Fracture and fatigue control in structures: applications of fracture mechanics[M]. [S.l.]: Prentice-Hall, 1987.
( 0) 0)
|
| [7] |
WANG Y Q, LIU X Y, HU Z W, et al. Experimental study on mechanical properties and fracture toughness of structural thick plate and its butt weld along thickness and at low temperatures[J]. Fatigue & fracture of engineering materials & structures, 2013, 36(12): 1258-1273. ( 0) 0)
|
| [8] |
WALLIN K. The scatter in KIC-results
[J]. Engineering fracture mechanics, 1984, 19(6): 1085-1093. DOI:10.1016/0013-7944(84)90153-X ( 0) 0)
|
| [9] |
ASTM. ASTM E 1921-18, Standard test method for determination of reference temperature, To, for ferritic steels in the transition range[S]. New York: R&B Inc., 2018.
( 0) 0)
|
| [10] |
SOKOLOV M, NANSTAD R. Comparison of Irradiation-induced Shifts of KJC and Charpy impact toughness for reactor pressure vessel steels[C]//Effects of Radiation on Materials: 18th International Symposium. West Conshohocken, PA, USA, 1999: 167−190.
( 0) 0)
|
| [11] |
SREENIVASAN P R. Estimation of ASTM E-1921 reference temperature from charpy tests: charpy energy-fracture toughness correlation method[J]. Engineering fracture mechanics, 2008, 75(18): 5229-5245. DOI:10.1016/j.engfracmech.2008.08.007 ( 0) 0)
|
| [12] |
AN Liqiang, JIANG W Q, LIU Y P, et al. Experimental study of mechanical behaviour of angles in transmission towers under freezing temperature[J]. Advanced steel construction, 2018, 14(3): 461-478. ( 0) 0)
|
| [13] |
LIU Xiyue, WANG Yuanqing, ZONG Liang, et al. Experimental study on mechanical properties and toughness of Q460C high-strength steel and its butt welded joint at low temperature[J]. International journal of steel structures, 2014, 14(3): 457-469. DOI:10.1007/s13296-014-3003-z ( 0) 0)
|
 2021, Vol. 48
2021, Vol. 48


