随着科技的发展及人们生活水平的提高，民用小型无人机由于获取便利、使用便捷而呈现爆发式增长。该类无人机在航拍、娱乐等领域已被广泛应用，在带来产业升级的同时，也带来了在机场等禁飞区“黑飞”的各种安全威胁^[1]。雷达系统是对该类无人机的管控与反制的常用手段之一，目标跟踪作为其中非常重要的一环，成为了一个备受关注的研究课题。

雷达目标跟踪是对目标的位置以及运动状态等参数进行估计，形成目标的运动轨迹。对目标进行跟踪过程中，噪声、目标的机动情况等会影响跟踪的结果。在雷达目标跟踪研究的初期，通常采用卡尔曼滤波算法对目标的运动状态进行估计和预测，建立起目标的运动轨迹。对于民用小型无人机这类的飞行器，由于受到人为操纵控制，并且自身运动性能不断提高，其机动性越来越强。民用小型无人机运动状态的复杂性和不确定性逐渐提高，这对雷达的跟踪性能有了更高的要求。卡尔曼滤波算法在目标运动状态比较单一时有很好的跟踪效果，当目标实施机动时(突然转弯或加、减速等)，卡尔曼滤波算法对目标的跟踪性能会下降^[2]。为了提高对目标运动状态描述的精确度，Blom等^[3]提出交互式多模型(interacting multiple model，IMM)结构算法，该方法使用2个或更多的运动模型来描述目标可能的运动状态，最后通过有效地加权融合对目标运动状态估计，很好地克服了单模型滤波算法估计误差较大的问题。交互式多模型算法是一种具有马尔可夫转移概率的结构自适应算法^[4]，目前在机动目标跟踪领域得到了广泛的应用。本文主要在IMM算法的基础上，对其在单目标雷达数据处理系统中的应用进行了分析和仿真。

1 交互式多模型算法 1.1 目标运动模型

在构造目标的状态方程之前，需要建立目标运动模型。目标运动模型是对目标运动特性的描述，是目标跟踪的基本要素之一^[5]。目标跟踪性能的优劣与目标运动模型建立的符合度有直接关系。目标运动模型的构造需要尽量还原目标实际的运动情况，同时应尽量简单以便进行数据处理。

假设在雷达探测范围内出现某种民用小型无人机在空中飞行，雷达系统将该无人机作为运动目标进行跟踪探测。当目标在空中做匀速直线运动时，可选用匀速(constant velocity，CV)运动模型描述目标的这种运动状态，这是目标跟踪中最基本的一种运动模型^[6]。

将运动目标在 $t$ 时刻的位置分量、速度分量、加速度分量分别表示为 $x(t)$ 、 $\dot x(t)$ 、 $\ddot x(t)$ 。因为目标做匀速直线运动，则 $\ddot x(t) = 0$ 。但运动目标会受到环境扰动带来的随机干扰，加速度具有随机特性的扰动输入，可以用连续时间白噪声 $w(t)$ 建模，并假设其服从均值为零的高斯分布，即 $\ddot x(t) = w(t)$ 。

此时连续时间的状态方程表示为^[7]

$\left[ {\begin{array}{*{20}{c}} {\dot x(t)} \\ {\ddot x(t)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&1 \\ 0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {x(t)} \\ {\dot x(t)} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right]w(t)$

目标的运动状态采用状态向量 ${{X}}(k) = {[\begin{array}{*{20}{c}} x&{\dot x} \end{array}]^{\rm{T}}}$ 来描述，得到离散时间状态方程为

${{X}}(k + 1) = {{F}}(k){{X}}(k) + {{W}}(k))$

式中： ${{W}}(k)$ 为过程噪声，其为均值为零、协方差矩阵为 ${{ Q}}$ 的高斯白噪声序列； ${{F}}(k) $ 为系统状态转移矩阵， ${{F}}(k) = \left[ {\begin{array}{*{20}{c}} 1&T \\ 0&1 \end{array}} \right]$ ，其中 $T$ 为采样间隔。

当目标在空中做匀加速直线运动时，可选用匀加速(constant acceleration，CA)运动模型描述目标的这种运动状态。此时加速度的一阶导数 $\dddot x(t) = 0$ 。考虑随机干扰的情况， $\dddot x(t)$ 是具有随机特性的扰动输入，可以用白噪声过程建模表示为 $\dddot x(t) = w(t)$ 。

此时连续时间的状态方程可表示为

$\left[ {\begin{array}{*{20}{c}} {\dot x(t)} \\ {\ddot x(t)} \\ {\dddot x(t)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&1&0 \\ 0&0&1 \\ 0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {x(t)} \\ {\dot x(t)} \\ {\ddot x(t)} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 1 \end{array}} \right]w(t)$

目标的运动状态采用状态向量 ${{X}}(k) \!=\! {[\begin{array}{*{20}{c}} x&{\dot x}&{\ddot x} \end{array}]^{\rm{T}}}$ 来描述，得到离散时间状态方程为

${{X}}(k + 1) = \left[ {\begin{array}{*{20}{c}} 1&T&{{T^2}/2} \\ 0&1&T \\ 0&0&1 \end{array}} \right]{{X}}(k) + {{W}}(k)$

状态方程是对运动目标的观测描述，而雷达系统对运动目标的观测过程通过量测方程表示。线性系统的量测方程表示为

${{Z}}(k) = {{H}}(k){{X}}(k) + {{V}}(k)$

式中： ${{Z}}(k)$ 为量测向量； ${{H}}(k)$ 为量测矩阵； ${{V}}(k)$ 为量测噪声序列，是对雷达在量测过程中存在误差的模拟，一般设置为均值为零、协方差矩阵为 ${{R}}$ 的高斯白噪声。

1.2 算法原理

IMM算法采用多个状态空间模型同时对目标的可能行为模式进行描述，不同的状态空间模型对应不同的卡尔曼滤波器^[8]。IMM算法的基本思想是：首先，在每一时刻通过对前一时刻所有滤波器的状态估计值混合，得出与相应模型所匹配的滤波器初始条件；然后，对每个模型按照滤波算法的步骤并行处理；最后，用模型匹配似然函数更新的模型概率作为加权值，对每个滤波器的状态估计值进行组合，得到的加权合并结果就是对目标状态的估计^[9]。本文设计的IMM算法中模型集由CV与CA组成，模型个数为N。IMM算法的一般步骤及计算公式如下。

1)输入交互。

对于算法模型集中的任意模型 $j$ ( $j = 1,2, \cdots , $ $ N$ )，由模型 $i$ ( $i = 1,2, \cdots ,N$ )到模型 $j$ 的混合概率为

${\mu _{ij}}(k - 1|k - 1) = \sum\limits_{i = 1}^r {{p_{ij}}{\mu _i}(k - 1)/{{\bar c}_j}} $

式中： $r$ 为状态空间模型个数； ${p_{ij}}$ 为模型 $i$ 到模型 $j$ 的转移概率； ${\mu _i}(k)$ 为当前时刻每个滤波器的模型概率。

${\bar c_j} = \sum\limits_{i = 1}^r {{p_{ij}}{\mu _i}(k - 1)} $

模型 $j$ 的混合状态估计：

$ {{\hat{{X}}}_{Oj}}(k - 1|k - 1) = \sum\limits_{i = 1}^r {{{{\hat{{X}}}}_i}(k - 1|k - 1)} \cdot {\mu _{ij}}(k - 1|k - 1) $

模型 $j$ 的混合协方差估计：

$ \begin{array}{*{20}{c}} {{{{P}}_{Oj}}(k - 1|k - 1) = \displaystyle\sum\limits_{i = 1}^r {{\mu _{ij}}(k - 1|k - 1)\{ {{{P}}_i}(k - 1|k - 1)} +}\\ {[{{\hat{{X}}}_i}(k - 1|k - 1) - {{\hat{{X}}}_{Oj}}(k - 1|k - 1)] \cdot [{{\hat{{X}}}_i}(k - 1|k - 1) -}\\ {{{\hat{{X}}}_{Oj}}(k - 1|k - 1){]^{\rm{T}}}\}} \end{array} $

2)对于模型 $j$ ，进行卡尔曼滤波。

状态预测：

${{\hat{{X}}}_j}(k|k - 1) = {{{F}}_j}(k - 1){{\hat{{X}}}_{Oj}}(k - 1|k - 1)$

预测误差协方差：

${{{P}}_j}(k|k - 1) = {{{F}}_j}{{{P}}_{Oj}}(k - 1|k - 1){{{F}}_j}^{\rm{T}} + {{{Q}}_j}(k - 1)$

残差：

${{{v}}_j}(k) = {{Z}}(k) - {{H}}(k){{\hat{{X}}}_j}(k|k - 1)$

残差协方差：

${{{S}}_j}(k) = {{H}}(k){{{P}}_j}(k|k - 1){{H}}{(k)^{\rm{T}}}{\rm{ + }}{{{R}}_j}(k)$

卡尔曼增益：

${{{K}}_j}(k) = {{{P}}_j}(k|k - 1){{H}}{(k)^{\rm{T}}}{{{S}}_j}{(k)^{ - 1}}$

状态更新：

${{\hat{{X}}}_j}(k|k) = {{\hat{{X}}}_j}(k|k - 1) + {{{K}}_j}(k){v_j}(k)$

预测误差协方差更新：

${{{P}}_j}(k|k) = {{{P}}_j}(k|k - 1) - {{{K}}_j}(k){{{S}}_j}(k){{{K}}_j}{(k)^{\rm{T}}}$

3)模型概率更新。

采用似然函数更新模型概率 ${\mu _j}(k)$ ，模型 $j$ 的似然函数为

${\varLambda _j}(k) = \frac{1}{{{{(2{{\text{π}} })}^{n/2}}|{{{S}}_j}(k){|^{1/2}}}} \cdot \exp \left\{ { - \frac{1}{2}{{{v}}_j}{{(k)}^{\rm{T}}}{{{S}}_j}{{(k)}^{ - 1}}{{{v}}_j}(k)} \right\}$

模型 $j$ 的概率更新为

${\mu _j}(k) = {\varLambda _j}(k){\bar c_j}/c$

式中 $c = \displaystyle\sum\limits_{j = 1}^r {{\varLambda _j}(k){{\bar c}_j}}$ 。

4)输出融合

总的状态估计：

${\hat{{X}}}(k|k) = \sum\limits_{j = 1}^r {{{{\hat{{X}}}}_j}(k|k){\mu _j}(k)} $

总的协方差估计：

$ \begin{array}{*{20}{c}} {{{P}}(k|k) = \displaystyle\sum\limits_{j = 1}^r {{\mu _j}(k)\{ {{{P}}_j}(k|k)} + }\\ { [{\hat{{{X}}}}_{j}(k|k)-\hat{{{X}}}(k|k)]\cdot {[{\hat{{{X}}}}_{j}(k|k)-\hat{{{X}}}(k|k)]}^{\rm{T}}\}} \end{array} $

2 坐标转换误差分析

在许多雷达跟踪系统中，目标的量测信息通常在极坐标系下获得，但在笛卡尔直角坐标系中对目标运动状态进行建模与跟踪滤波处理，需要利用坐标变换的方法将极坐标下的量测值转换成直角坐标形式。由于雷达在极坐标系下量测的数据中含有噪声，转换至直角坐标系下的数据有误差存在，这成为雷达跟踪系统必须考虑的问题^[10]。

设二坐标雷达在极坐标系下对目标进行量测，得到的测量距离为 ${r_{\rm{m}}}$ ，测量方位角为 ${\theta _{\rm{m}}}$ ，且有

$ \begin{array}{*{20}{c}} {{r_{\rm{m}}} = r + \tilde r}\\ {{\theta _{\rm{m}}} = \theta + \tilde \theta } \end{array} $

式中： $r$ 为目标真实的距离； $\theta $ 为目标真实的方位角； $\tilde r$ 、 $\tilde \theta $ 为相应的测量误差，且其是不相关的零均值高斯分布，方差分别为 $\sigma _r^2$ 与 $\sigma _\theta ^2$ 。

通过极−直坐标转换，可得直角坐标系下目标位置的测量值为

${x_{\rm{m}}} = {r_{\rm{m}}}\cos {\theta _{\rm{m}}}$

(1)

${y_{\rm{m}}} = {r_{\rm{m}}}\sin {\theta _{\rm{m}}}$

(2)

由于式(1)与式(2)中包含了非线性转换，如果直接将转换的数据作为跟踪算法的目标观测数据进行滤波，则得到的滤波估计结果为有偏估计^[11]。因此需要对这种转换的误差进行分析，然后对误差进行补偿，得到目标观测状态的无偏转换数据。

设 ${x_{\rm{e}}}$ 、 ${y_{\rm{e}}}$ 是直角坐标系的误差，则有

$ \begin{array}{*{20}{c}} {{x_{\rm{m}}} = x + {x_{\rm{e}}} = (r + \tilde r)\cos (\theta + \tilde \theta )}\\ {{y_{\rm{m}}} = y + {y_{\rm{e}}} = (r + \tilde r)\sin (\theta + \tilde \theta )} \end{array} $

按三角函数的和角公式展开得

$ \begin{array}{*{20}{c}} {{x_{\rm{e}}} = r\cos \theta (\cos \tilde \theta - 1) - \tilde r\sin \theta \sin \tilde \theta - }\\ {r\sin \theta \sin \tilde \theta + \tilde r\cos \theta \cos \tilde \theta }\\ {{y_{\rm{e}}} = r\sin \theta (\cos \tilde \theta - 1) - \tilde r\cos \theta \sin \tilde \theta -}\\ {r\cos \theta \sin \tilde \theta + \tilde r\sin \theta \cos \tilde \theta } \end{array} $

因为 $\tilde r \sim N(0,{\sigma _r})$ ， $\tilde \theta \sim N(0,{\sigma _\theta })$ ，可以得到

${\rm{E}}[\cos \tilde \theta ] = - \frac{1}{{\sqrt {2{{\text{π}} }} {\sigma _\theta }}}\int {\cos \tilde \theta \exp \Bigg( - \frac{{{\theta ^2}}}{{2\sigma _\theta ^2}}\Bigg)} {\rm{d}}\tilde \theta = \exp \Bigg( - \frac{{\sigma _\theta ^2}}{2}\Bigg)$

同理可得：

$ \begin{array}{*{20}{c}} {{\rm{E}}[\sin \tilde \theta ] = 0}\\ {{\rm{E}}[\sin \tilde \theta \cos \tilde \theta ] = 0}\\ {{\rm{E}}[{\cos ^2}\tilde \theta ] = \dfrac{{1 + \exp ( - 2\sigma _\theta ^2)}}{2}}\\ {{\rm{E}}[{\sin ^2}\tilde \theta ] = \dfrac{{1 - \exp ( - 2\sigma _\theta ^2)}}{2}} \end{array} $

因此，转换后的直角坐标误差( ${x_{\rm{e}}}$ , ${y_{\rm{e}}}$ )在真值( $r$ , $\theta $ )条件下的均值为

${{{\mu}} _r} = \left[ {\begin{array}{*{20}{c}} {{\rm{E}}[{x_{\rm{e}}}|r,\theta ]} \\ {{\rm{E}}[{y_{\rm{e}}}|r,\theta ]} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {r\cos \theta \Bigg[\exp \Bigg( - \dfrac{{\sigma _\theta ^2}}{2}\Bigg) - 1\Bigg]} \\ {r\sin \theta \Bigg[\exp \Bigg( - \dfrac{{\sigma _\theta ^2}}{2}\Bigg) - 1\Bigg]} \end{array}} \right]$

以上是在真值( $r$ , $\theta $ )条件下求取的均值，在工程实践中无法直接应用。为了获取能在实践中使用的结果，在量测数据( ${r_m}$ , ${\theta _m}$ )的条件下求取 ${x_{\rm{e}}}$ 和 ${y_{\rm{e}}}$ 的均值。

在 $ {\mu _r}$ 中，用( ${r_m} - \tilde r$ )代换 $r$ ，用( ${\theta _m} - \tilde \theta $ )代换 $\theta $ ，根据三角函数和差化积公式，可求得坐标转换的转换误差为

$ \begin{array}{*{20}{c}} {{{{\mu}} _\mu } = \left[ {\begin{array}{*{20}{c}} {{\rm{E}}[{x_{\rm{e}}}|{r_{\rm{m}}},{\theta _{\rm{m}}}]} \\ {{\rm{E}}[{y_{\rm{e}}}|{r_{\rm{m}}},{\theta _{\rm{m}}}]} \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} {{r_{\rm{m}}}\cos {\theta _{\rm{m}}}\Bigg[\exp ( - \sigma _\theta ^2) - \exp \Bigg( - \dfrac{{\sigma _\theta ^2}}{2}\Bigg)\Bigg]} \\ {{r_{\rm{m}}}\sin {\theta _{\rm{m}}}\Bigg[\exp ( - \sigma _\theta ^2) - \exp \Bigg( - \dfrac{{\sigma _\theta ^2}}{2}\Bigg)\Bigg]} \end{array}} \right]} \end{array} $

因此，雷达量测数据坐标转换的无偏转换公式为

$\left[ {\begin{array}{*{20}{c}} {{x_z}} \\ {{y_z}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{r_{\rm{m}}}\cos {\theta _{\rm{m}}}} \\ {{r_{\rm{m}}}\sin {\theta _{\rm{m}}}} \end{array}} \right] - {{{\mu}} _\mu }$

即直角坐标( ${x_z}$ , ${y_z}$ )是极坐标( ${r_{\rm{m}}}$ , ${\theta _{\rm{m}}}$ )的无偏转换， ${\mu _\mu }$ 为坐标转换的转换误差。

转换误差的协方差矩阵为^[12]

${{R}} = \left[ {\begin{array}{*{20}{c}} {R(1,1)}&{R(1,2)} \\ {R(2,1)}&{R(2,2)} \end{array}} \right]$

式中：

$ \begin{array}{*{20}{c}} {R(1,1) = \dfrac{1}{2}(r_{\rm{m}}^2 + \sigma _r^2)(1 + {\lambda _\theta }^\prime \cos 2{\theta _{\rm{m}}}) + (\lambda _\theta ^{ - 2} - 2)r_{\rm{m}}^2{\cos ^2}{\theta _{\rm{m}}}}\\ {R(2,2) = \dfrac{1}{2}(r_{\rm{m}}^2 + \sigma _r^2)(1 - {\lambda _\theta }^\prime \cos 2{\theta _{\rm{m}}}) + (\lambda _\theta ^{ - 2} - 2)r_{\rm{m}}^2{\sin ^2}{\theta _{\rm{m}}}}\\ {R(1,2) = \dfrac{1}{2}(r_{\rm{m}}^2 + \sigma _r^2){\lambda _\theta }^\prime \sin 2{\theta _{\rm{m}}} + (\lambda _\theta ^{ - 2} - 2)r_{\rm{m}}^2\sin {\theta _{\rm{m}}}\cos {\theta _{\rm{m}}}}\\ {R(2,1) = R(1,2)}\\ {{\lambda _\theta } = \exp ( - \sigma _\theta ^2/2)}\\ {{\lambda _\theta }^\prime = \exp ( - 2\sigma _\theta ^2)} \end{array} $

3 单目标雷达数据处理系统仿真

假定使用二坐标雷达对低空飞行的民用小型无人机进行观测。目标的起始点为(500 m，2 000 m)，在 $t = 0 \sim 50$ s沿y轴以运动速度为 $ - 20$ m/s做匀速直线运动；在 $t = 50 \sim 60$ s向x轴方向做90°的慢转弯运动，加速度 ${a_x} = {a_y} = 2$ m/s²，完成慢转弯后加速度将降为零；在 $t = 60 \sim 66$ s沿x轴做匀速运动；从 $t = 66$ s开始做 $90^\circ $ 的快转弯运动，加速度为 ${\rm{5}}$ m/s²；在 $t = 70$ s结束转弯，加速度降为零；在 $t = 70 \sim 110$ s沿y轴做匀速直线运动。雷达扫描周期 $T = 2$ s，目标距离与方位角测量噪声的标准差分别为 ${\sigma _r} = 10$ m， ${\sigma _\theta }$ =1°。转换误差的协方差矩阵为

${{R}} = \left[ {\begin{array}{*{20}{c}} {1\;199}&{{\rm{ - }}283} \\ {{\rm{ - }}283}&{173} \end{array}} \right]$

IMM滤波算法采用3个模型对目标的运动状态进行描述：第一个模型是非机动的CV模型，过程噪声的方差为零；第二、三个模型均为CA机动模型，但过程噪声的方差不同，第二个模型的过程噪声方差为 $Q$ =0.001 ${I_{2 \times 2}}$ ，第三个模型的过程噪声方差为 $Q$ =0.0114 ${I_{2 \times 2}}$ 。控制模型转换的马尔可夫链的转移概率矩阵为

${{P}} = \left[ {\begin{array}{*{20}{c}} {0.8}&{0.1}&{0.1} \\ {0.1}&{0.8}&{0.1} \\ {0.1}&{0.1}&{0.8} \end{array}} \right]$

设定各模型的模型概率初始值分别为 ${\mu _1} = 0.5$ 、 ${\mu _2} = 0.25$ 、 ${\mu _3} = 0.25$ 。

定义滤波误差的均值为

${e_x}(k) = \frac{1}{M}\sum\limits_{i = 1}^M {\left[ {{x_i}(k) - {{\hat x}_i}(k|k)} \right]} $

定义滤波误差的标准差为

${\sigma _{\hat x}} = \sqrt {\frac{1}{M}\sum\limits_{i = 1}^M {{{[{x_i}(k) - {{\hat x}_i}(k|k)]}^2}} - {{\left[ {{e_x}(k)} \right]}^2}} $

式中： $M$ 为蒙特卡洛模拟次数； $k = 1,2, \cdots ,N$ ， $N$ 为采样次数。

进行1 000次蒙特卡洛仿真实验，得到运动目标在极坐标下的真实轨迹、观测轨迹及一次滤波估计结果曲线，如图1—图3所示。其中，图3滤波估计结果是在无偏坐标转换的条件下得出的。

从图3中可以看出，无论目标在非机动还是机动状态，滤波轨迹相对于观测轨迹更加接近于目标真实轨迹，具有较好的滤波效果，说明了IMM算法能够实现对雷达单目标进行有效的跟踪。

IMM算法的滤波过程包括了对目标状态原始数据初始化、目标状态预测及目标状态更新。在极坐标下对目标距离、方位角滤波过程的误差分析曲线如图4所示。

图4曲线表示了滤波过程中的误差。目标观测状态是由雷达系统测量得到的，通过初始误差曲线可以看出，在各个时刻目标量测误差都较大。预测误差曲线是由IMM算法对目标状态的预测所形成的，当目标处于机动状态时，IMM算法的预测结果会出现较大的误差。在滤波过程中IMM算法利用观测数据对预测状态进行修正。对比预测误差曲线与更新误差曲线可以看出：在目标机动时滤波得到的目标状态估计结果比预测结果的误差要小；当目标状态由机动转换至非机动时，目标状态估计误差会趋近于零。

在极坐标下，方位角滤波误差标准差曲线和距离误差标准差曲线如图5和图6所示。

图5是在极坐标下对方位角误差标准差的分析曲线。分别将方位角在测量、有偏估计和无偏估计的条件下进行滤波误差标准差分析。方位角测量值的误差标准差约为1°，与仿真条件中设置的方位角量测噪声标准差相符。对量测值进行极−直坐标转换，通过交互式多模型算法对转换结果进行滤波处理，得到的方位角估计误差标准差约为0.7°。由于量测值直接进行坐标转换存在转换误差，因此对转换误差补偿之后再用滤波算法处理，得到的方位角无偏估计误差标准差约为0.55°，这比测量值与有偏估计值更加接近于目标运动状态的真实值。

同样，由图6可以看出，在极坐标下距离测量误差标准差约为10 m，量测值通过坐标转换及滤波处理后，距离的有偏估计误差标准差约为6.5 m，而对坐标转换误差补偿之后滤波得到的距离误差标准差稍小，说明无偏估计结果更精确一些。目标在第二次转弯时要比第一次转弯更急，因此在误差标准差曲线上产生了更大的波动；在滤波进入稳定状态之后，误差标准差又减小，这体现出IMM算法受目标机动的影响很小。

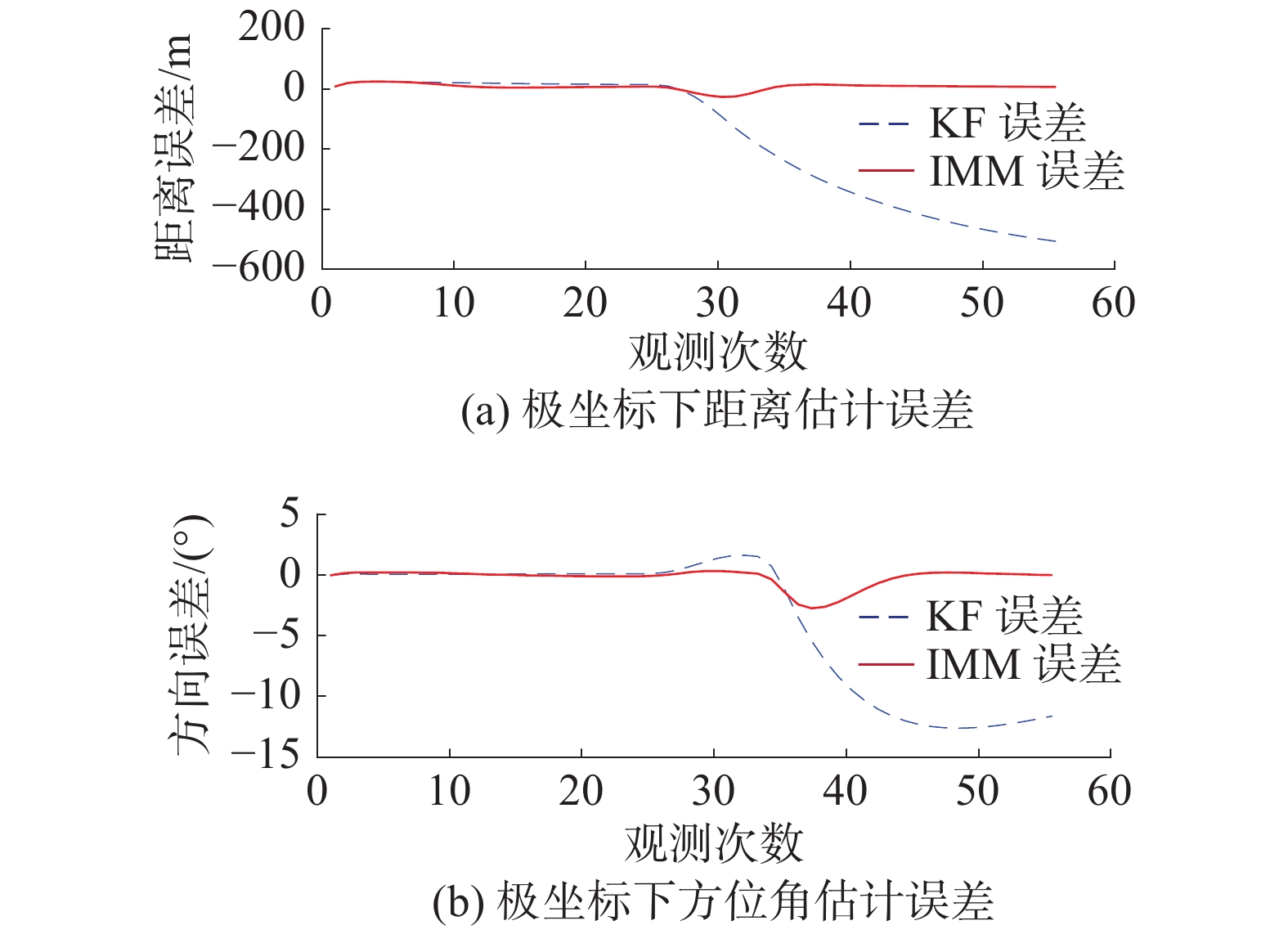
为了比较交互式多模型算法与卡尔曼滤波算法对雷达目标的跟踪性能，分别将雷达目标的量测值使用这2种算法进行滤波处理，得到目标位置估计结果在极坐标下的估计误差如图7所示。

由图7的估计误差曲线可以看出：雷达目标在初始阶段的匀速运动状态下，交互式多模型算法与卡尔曼滤波算法的估计误差都比较小；但目标进行机动运动之后，卡尔曼滤波算法对目标机动的适应性较低，因此估计误差逐渐增大，使其失去对目标跟踪的能力，而交互式多模型算法对机动目标有很好的适应性，得到估计结果的误差较小，能够实现对目标进行有效跟踪。

为了分析交互式多模型算法在实际应用时的可行性，在外场环境实验中，将低空飞行的大疆公司小型无人机作为雷达目标，利用线性调频连续波雷达对该目标进行观测，无人机在一个运动过程通过实测数据形成的目标运动轨迹如图8所示。

无人机在这个运动过程中通过飞行记录所显示的目标真实运动轨迹如图9所示。

通过卡尔曼滤波算法与交互式多模型算法对雷达目标实测数据进行跟踪滤波处理，得到的滤波估计结果所形成的目标运动轨迹如图10所示。由图10可以看出，卡尔曼滤波算法的滤波估计轨迹出现了很大的偏差，交互式多模型算法的滤波估计轨迹与目标飞行记录显示的运动轨迹比较符合。这是由于卡尔曼滤波算法在滤波过程中只通过单一模型对目标的运动状态进行估计，但是无人机的真实运动状态会出现机动情况，只通过单一模型不能概括目标所有的运动状态，使得滤波结果会出现较大的误差，还可能出现滤波发散的现象。交互式多模型算法能够采用多个目标运动模型对目标的运动状态进行滤波估计，因此在目标出现机动运动状态时该滤波算法能实现对目标运动状态的估计，并且滤波误差较小。

4 结论

本文对交互式多模型算法在雷达单目标跟踪中的应用情况进行了描述。针对民用小型无人机的跟踪问题，对目标的运动模型进行介绍，分析了量测数据坐标转换的转换误差，并给出无偏坐标转换公式。通过蒙特卡洛仿真实验对交互式多模型算法在机动目标跟踪时的跟踪性能进行分析，仿真结果表明，滤波估计轨迹相对于观测轨迹更加接近于目标真实轨迹，并且不会有大的偏差，实现了对机动目标的跟踪能力，证明了算法估计的有效性。

通过外场环境实验所得到的实测数据对卡尔曼滤波算法与交互式多模型算法的目标跟踪性能进行比较，实测数据分析结果表明交互式多模型算法能够实现对雷达单目标进行有效的跟踪，说明了该算法在雷达目标跟踪过程的实用性，体现出一定的工程应用价值。