近年来随着科技的发展,小型无人机逐渐出现在大众的视野中。为大众带来方便的同时,也有些非合作无人机会给一些敏感地区的低空安全带来很大的威胁。与其他无人机反制方案相比,雷达探测相比于其他手段具有全天候、作用距离大的优势[1]。但低、慢、小目标的探测一直是雷达信号处理的难点,尤其是在无人机悬停的场景下,无人机回波在多普勒频率上和地杂波混合在一起,为目标检测带来了很大的困难。不过无人机高速转动的旋翼会给雷达回波带来额外的频率调制,使其多普勒特征不同于一般物体的雷达回波[2-3]。美国的著名学者Victor.C.Chen[4]在其著作中将其命名为“微多普勒效应”。目前国内和国际上对于无人机旋翼回波特征的研究大多在仿真阶段,有实测数据的研究也都是对算法的佐证,实时性不强[5]。因此本文根据无人机回波的特点,结合相关文献的研究结果,分析了无人机旋翼回波的频域特性,根据无人机回波特点,选择在FPGA上构造一阶递归型MTI滤波器对背景杂波进行抑制,利用第三代双倍速率(double data rate, DDR3)存储器实现多周期雷达回波的MTD处理,在处理速度和吞吐率上进行了一定的优化,将FPGA处理后的距离–多普勒(range-Doppler,R-D)二维谱和理论R-D谱比较分析,证明FPGA处理结果的正确性。本文所述LFMCW雷达系统的信号处理板是基于FPGA+DSP架构的,FPGA负责信号的高速采集和处理,DSP负责目标的参数估计以及系统主控。其中FPGA为Xilinx V7系列的XC7V585T-2FFG1761I,开发平台为Vivado 2019.2。
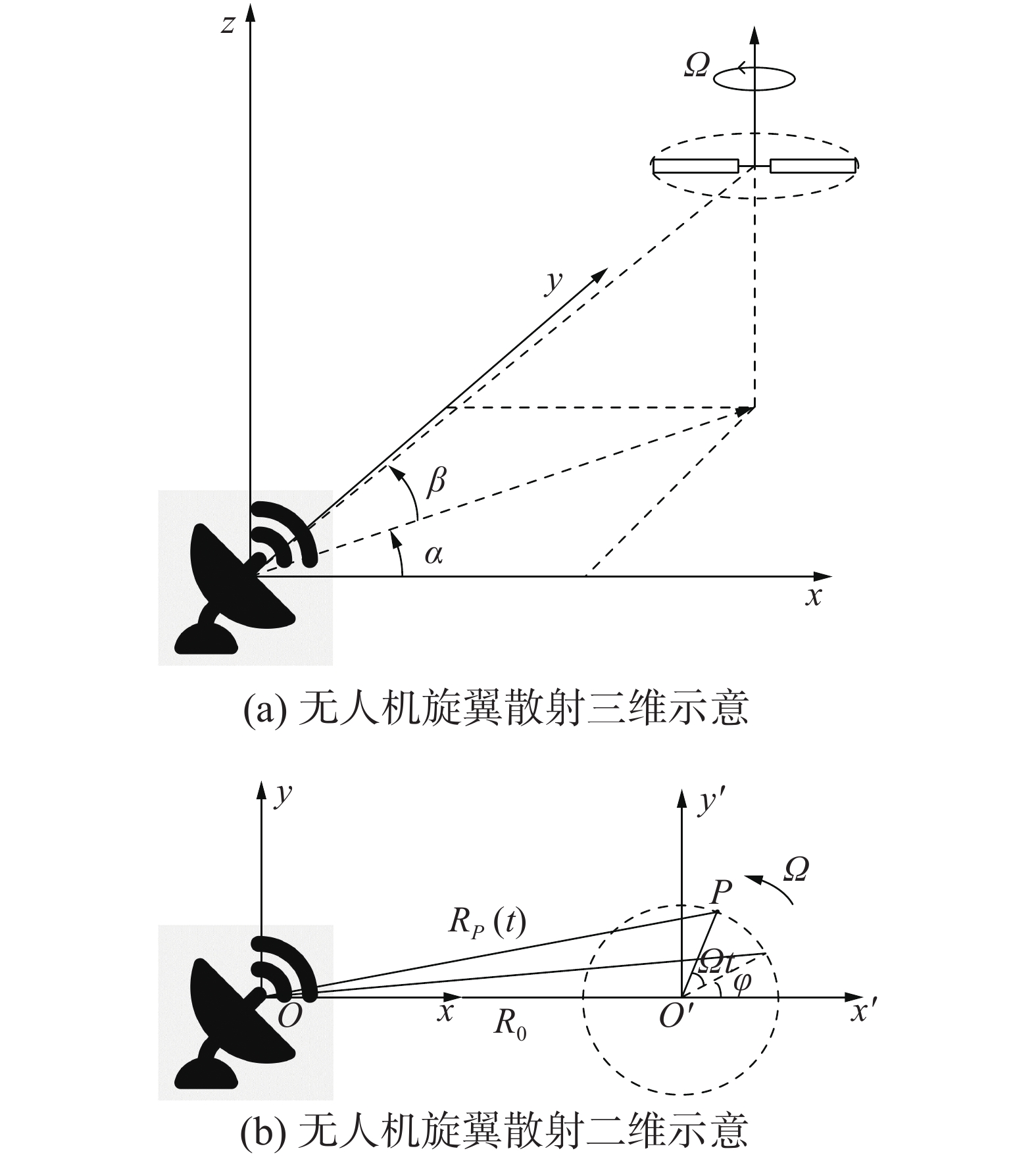
1 无人机雷达回波分析考虑到无人机的低、慢、小特性,本文选用的雷达体制为LFMCW雷达。因为其无距离盲区,适合观测近处无人机目标。而相比单频连续波雷达,LFMCW雷达不仅能够观测到目标的多普勒特性,还能得到目标的距离信息,更适用于监测无人机状态的雷达应用场景。根据文献[6-9]中的结论可知,无人机的时域回波特征是“闪烁”效应,理论上讲提取时域特征对雷达硬件的要求更低。但在实际场景中,时域特征不如频域特征稳定和易于分析。故本文仅分析无人机回波的频域特征。无人机旋翼在雷达观测下的几何示意图如图1所示。
|
Download:
|
| 图 1 无人机旋翼散射点示意 | |
由图1可知,无人机距离雷达的方位角为α,俯仰角为β,模拟角速度为
| $\begin{gathered} {R_P}(t) = \sqrt {R_0^2 + {r^2} + 2{R_0}r\cos \left( {\varOmega t + \varphi } \right)} \approx \\ {R_0} + r\cos \left( {\varOmega t + \varphi } \right) \end{gathered} $ |
忽略初相,对P点处的回波与发射信号进行差频处理并化简后,得到差频信号表达式:
| ${s_P}(t) = \rm{exp}\left[ {\frac{{{\rm{j}}2{\rm{{\text{π}} }}}}{c}\left( \begin{gathered} 2{f_0}({R_0} + r\cos (\varOmega t) + \mu t({R_0} + r\cos (\varOmega t)) \\ \end{gathered} \right)} \right]$ |
式中:μ=B/T为调频斜率,其中,B为调频带宽,T为调频周期;c为光速。
对整个叶片的散射点做积分可得到整个旋翼的回波表达式:
| $\begin{gathered} S(t) = \int\limits_0^l {{S_r}(t)} {\rm{d}}r = l\operatorname{sinc} \Bigg(2{\rm{{\text{π}} }}\frac{{{f_0} + \mu t}}{c}l\cos (\varOmega t)\Bigg) \cdot \\ \exp \Bigg({\rm{j}}2{\rm{{\text{π}} }}\frac{{{f_0} + \mu t}}{{\rm{c}}}l\cos (\varOmega t)\Bigg)\exp \Bigg({\rm{j}}2{\rm{{\text{π}} }}\frac{{{f_0} + \mu t}}{c}2{R_0}\Bigg) \end{gathered} $ | (1) |
对于多叶片的情况,回波表达式仅初相φ的值不同。设一个旋翼上的叶片数目为N,则第k个叶的初相φk为
| ${\varphi _k} = \varphi + 2k{\text{π}} /N \quad (k = 0,1, \cdots ,N)$ |
本文研究的无人机为大疆精灵3标准版,叶片数为2。下面代入实际雷达参数对无人机旋翼回波进行仿真。仿真参数如表1所示。
|
|
表 1 仿真参数 |
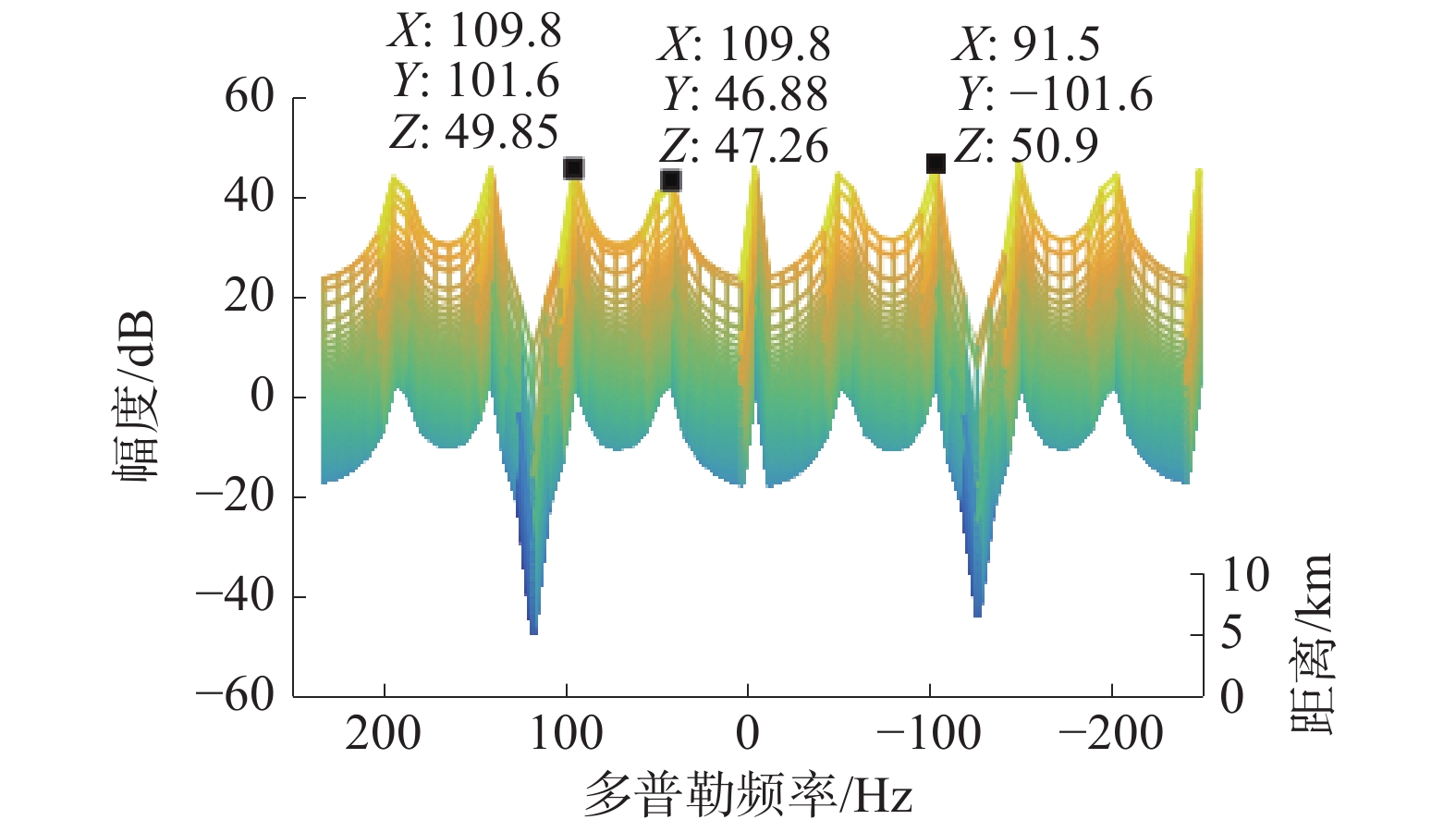
需要说明的是,为减少LFMCW雷达距离–速度耦合的影响,本文雷达选用三角调频的方式,上下调频周期各1 ms。后文给出的仿真和实测均为上扫频结果。为保证差频信号频谱的纯净,需要将1 ms内2 500个时域采样点头尾数据删去,用中间段2 048个点做FFT。暂不考虑叶片的实际散射截面积(radar cross section,RCS)和噪声,将仿真参数代入式(1),经过快时间距离维快速傅里叶变换(fast Fourier transform,FFT)和慢时间多普勒维FFT后得到无人机旋翼回波的R-D谱。仿真结果如图2所示。
|
Download:
|
| 图 2 单个无人机旋翼的R-D谱 | |
从图2的仿真结果可以看出,无人机旋翼回波的谱峰在多普勒域上是成对出现的,并关于零频对称。这与文献[2]中理论分析的结果一致。谱峰间隔为54.72 Hz,按照文献[10]分析的结果,谱峰间隔Δf应为Δf=NBfrot。按此计算无人机旋翼转速应为27.36 r/s,和仿真参数相近。
2 无人机回波处理的FPGA实现本文选择在FPGA上而非DSP上实现MTI和MTD处理,目的是提高算法的运算速度,为DSP进行更加复杂的算法争取时间。下面分别叙述系统整体结构和数据处理流程,以及MTI、MTD的FPGA实现方法。
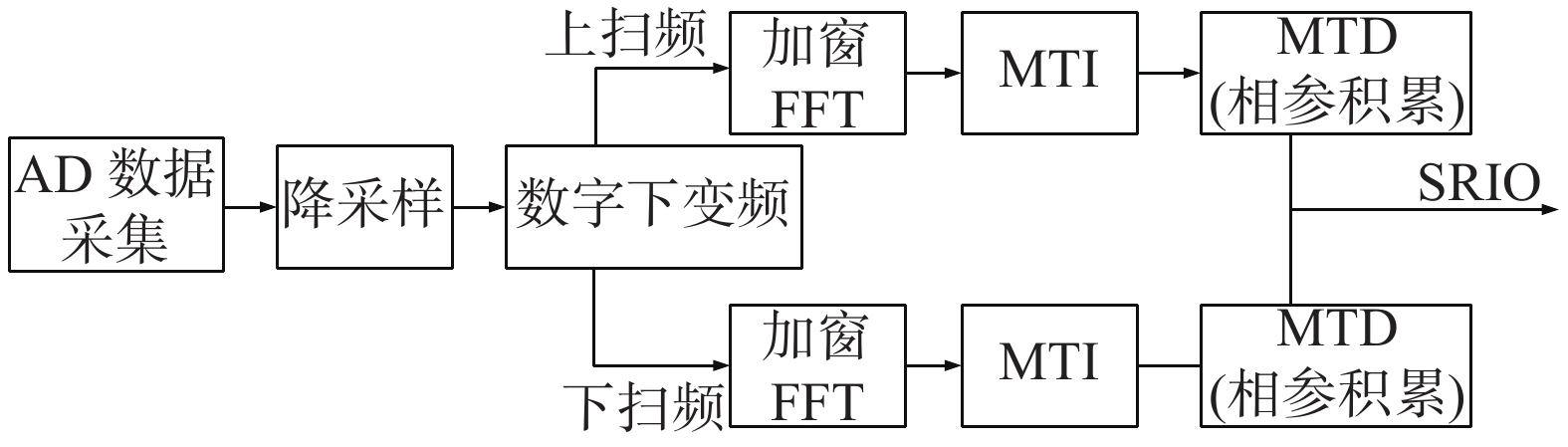
2.1 FPGA整体处理流程LFMCW雷达信号处理包括一维FFT、MTI杂波抑制和MTD相参积累处理。一维FFT的作用是获取包含在回波频域的目标距离信息,同时提高目标信号的信噪比增益,类似脉冲雷达的脉冲压缩处理。MTI则是通过构造多普勒域高通滤波器,达到抑制零频杂波的目的。MTD可以视为是多普勒滤波器组,将不同多普勒频率的信号进行同相叠加输出,得到目标的多普勒信息,区分开不同多普勒频率的目标,也是获取无人机微多普勒特征的重要手段。系统的整体结构如图3所示。
|
Download:
|
| 图 3 系统整体结构 | |
回波信号经天线进入到接收机,与发射机输入到接收机的本振信号混频、滤波,得到差频信号。数模转换器(analog to digital converter,ADC)将模拟差频信号转化为数字信号后将数字信号传给FPGA,FPGA对串行的AD原始数据进行串并转换、降采样、数字下变频,得到同相(I路)和正交(Q路)分量。参照FPGA内部产生的上下扫频指示信号,将上下2个扫频段的连续波信号分别进行加汉明窗抑制旁瓣、距离维FFT运算、MTI杂波抑制、MTD相参积累。最后通过串行高速总线(serial rapidIO,SRIO)接口将MTD后的数据发送给DSP进行后续信号处理。
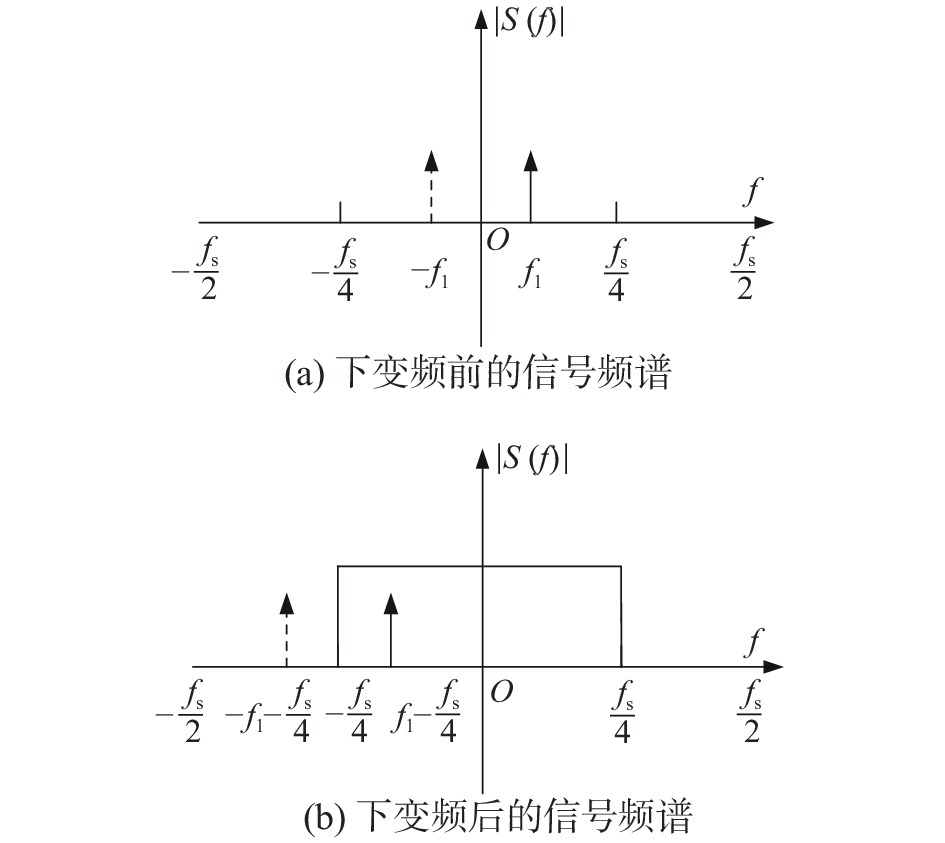
本文雷达接收机为零中频结构,直接采集实信号。若直接对实信号做FFT,则会产生镜像频率分量,即在频域有多个峰值。因此需要对回波进行数字下变频得到复信号,经过低通滤波器滤除镜像频率后再进行FFT运算。数字下变频过程中,差频信号的频谱变化如图4所示。
|
Download:
|
| 图 4 频信号频谱变化过程 | |
图中|S( f )|为差频信号频谱的幅度,f1为一个目标距离对应的差频信号频率。实线为正频率谱峰,虚线为镜像频率的谱峰。系统中AD采样频率为60 MHz,经过降采样处理后数据速率下降到2.5 Hz,与图中fs相对应。将降采样后的2.5 Hz数据在2.5 MHz时钟下分别乘1、0、−1、0,即与cos(2πfst/4)相乘,可以得到I路输出;分别乘0、−1、0、1,即与−sin(2πfst/4)相乘,可以得到Q路输出。在频域上的频谱搬移效果如图4所示,关于0频率对称的谱峰被搬移到关于−fs/4对称。在经过截止频率为fs/4的低通滤波器后,镜像频率即被抑制,目标距离所对应的频率由0~fs/2变为−fs/4~fs/4。在经过FFT后仅对这部分频率的FFT结果进行后续处理即可。
2.2 MTI处理的FPGA实现MTI可由相邻脉冲对消来实现。常用的MTI滤波器有两脉冲对消、三脉冲对消等。对消次数越多,滤波器在零频处的凹陷越深,凹口越大,能够滤除的杂波范围也更大。但脉冲对消的缺陷也很明显。首先是通带不够平坦,而且对消次数越多越不平坦,无人机的旋翼信息很可能因此损失,恒虚警检测时也容易将背景估计过高或过低,造成漏警或虚警;其次是对于无人机这种低、慢、小目标,其低速运动时的多普勒频率很低,很容易被MTI滤波器抑制,造成雷达跟踪过程中航迹断裂。若想解决这个问题,需要实现对MTI滤波器的凹口大小和平坦度的实时调整。文献[11]中提到了一种递归型MTI滤波器的构造方法,在两脉冲对消器基础上引入了一条反馈支路,反馈系数为K。通过给系统函数增加新的极点z=K的方法实现了频率响应的平坦化处理。递归MTI滤波器的结构如图5所示。

|
Download:
|
| 图 5 递归型MTI滤波器的结构 | |
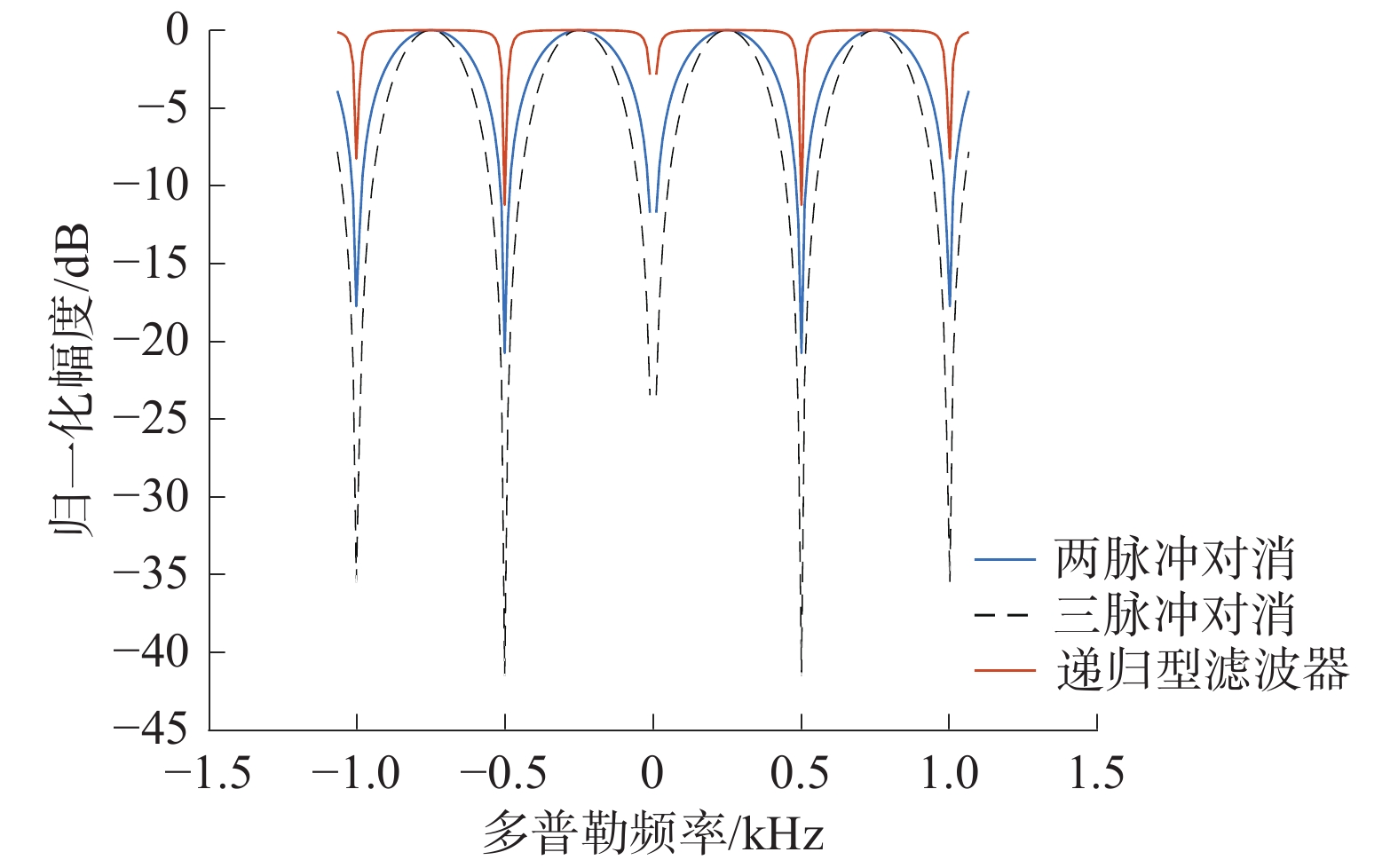
根据递归型MTI滤波器的结构可以得到其频率响应,K取0.8时,其频率响应和脉冲对消器的对比如图6所示。两脉冲对消器的极点为z=0,递归型MTI滤波器的极点为z=0和z=K。K的取值越接近1,2个极点的距离越远,系统的频率响应就越平坦,零频凹口就越小;反之系统频率响应就越不平坦,零频凹口就越大。在LFMCW雷达系统工作时,可以根据杂波幅度大小和杂波多普勒频率的范围,灵活地更改K的值以获取不同的杂波抑制效果,更适合本文所述的无人机探测场景。
|
Download:
|
| 图 6 不同MTI滤波器的频率响应对比 | |
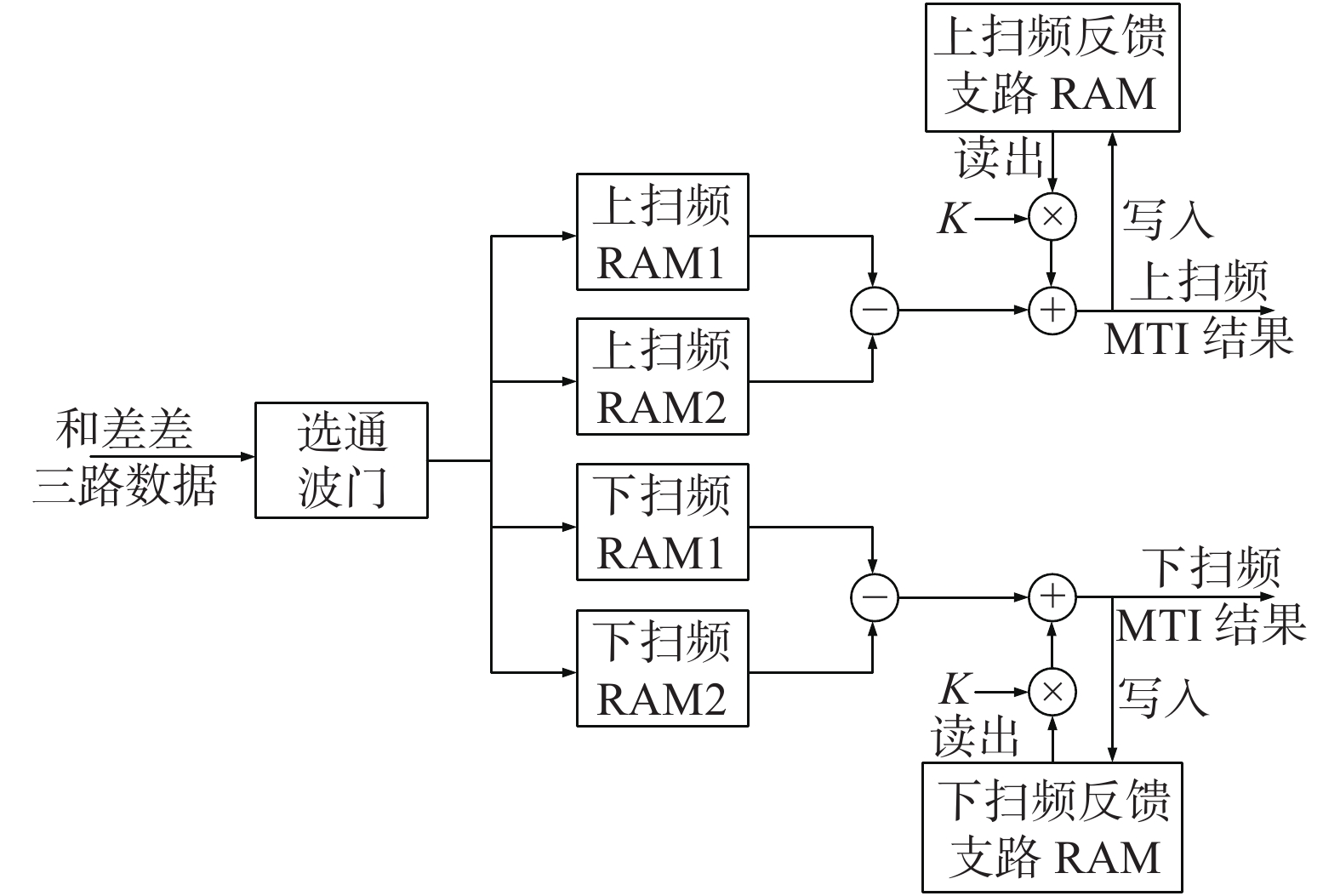
在FPGA上实现递归型MTI滤波器需要进行相邻周期脉冲的相减、反馈支路数据的保存和与反馈系数相乘等工作。本文选用双端口随机存储器(radom access memory,RAM)来缓存回波数据,经过前面预处理的回波经过波门选通逻辑写入不同的RAM,反馈支路也选用双端口RAM保存。本文在从端口B读取出反馈支路RAM数据的同时,将新计算的MTI处理结果通过端口A写入RAM。无论是计算MTI还是更新反馈支路数据,都采用流水线处理的方式,最大限度地提高处理速率。综上,在FPGA上实现MTI处理的信号流向,如图7所示。
|
Download:
|
| 图 7 FPGA实现MTI信号流向 | |
为验证FPGA程序设计的正确性,需要借助ModelSim平台对设计进行仿真。仿真时输入的3路回波数据为实测的室内开机下的雷达回波。FPGA对回波进行数字下变频、距离维FFT后,不经后续处理直接截取每个回波的前256个距离门数据上传上位机。ModelSim仿真时仅需要在测试文件中给出时钟和输入的一维FFT数据,其余参数都由FPGA程序设计决定,与表1中参数相同。杂波数据如图8所示。
|
Download:
|
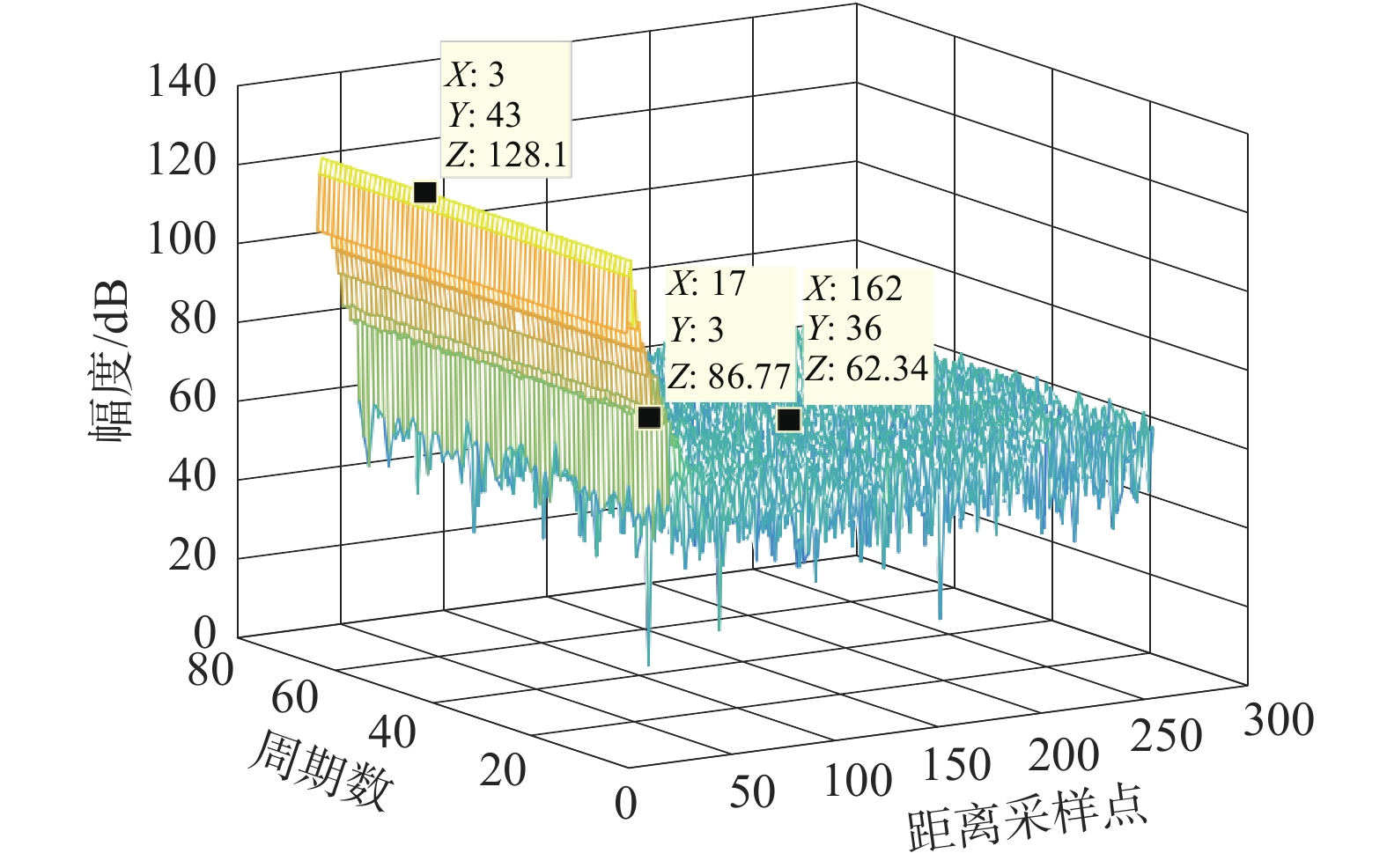
| 图 8 用于仿真的实测杂波数据 | |
从图8中可以看出杂波的峰值出现在第3个距离采样点,且能量分布在1~17个距离采样点,远远高于背景噪声,且不同周期的杂波幅度相近,符合固定目标回波特性,也间接证明了硬件系统的有效性和FPGA前端处理的正确性。将杂波数据作为激励输入到testbench中,得到的仿真结果如图9所示。

|
Download:
|
| 图 9 MTI处理ModelSim仿真 | |
图9是以一次上扫频的MTI处理为例,当新的回波数据到来时,FPGA先将数据写入上扫频RAM1。写完后将上扫频RAM1和RAM2的数据一同读出输入到减法器中,与此同时读取上扫频反馈支路RAM中的数据乘以系数0xCCCC(即为16位无符号定点小数0.8),再和减法器输出的数据一同输入到加法器中。最后得到的add_I_out和add_Q_out的结果即为最后MTI处理后的回波数据。可以看到在同一显示尺度下,原始回波I、Q路的高强度杂波已经得到了滤除。另外需要说明的是,反馈支路RAM存在同时读写的情况,但新的MTI结果一定是在读取反馈支路RAM的数据后才会输出,所以并不存在对RAM中同一个地址同时读写的情况,局部放大的结果如图10所示。

|
Download:
|
| 图 10 反馈支路RAM读写局部放大 | |
图10中addra,wea,dina分别对应双端口RAM的A端口的地址、写使能和数据线。同理另外3组信号对应B端口的地址、读使能和数据。可以看到写使能wea是在读使能enb拉高后几个时钟才拉高。
对以上仿真结果进行时钟计数,发现通过流水线并行处理,FPGA能够在10 μs左右完成对雷达回波的递归MTI处理,达到快速实现MTI的目的。
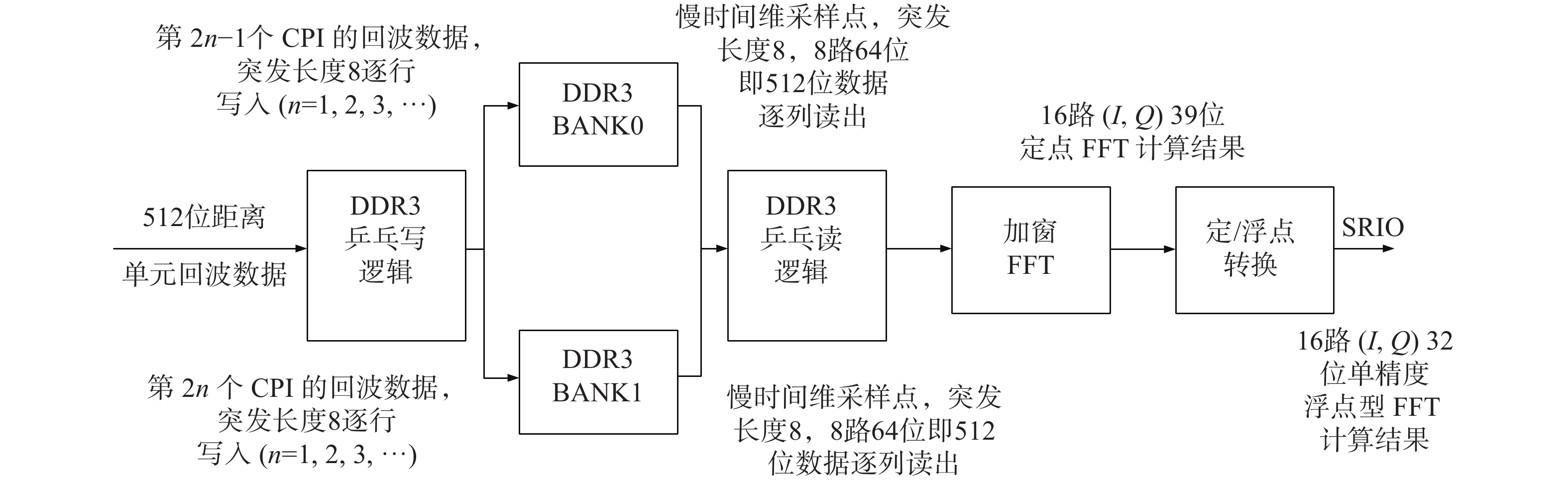
2.3 MTD处理的FPGA实现对于传统的信号处理机,MTD处理多由DSP或嵌入式进阶精简指令集机器(advanced RISC machine,ARM)等处理器去完成。但串行逻辑在处理这种大量重复运算时的效率会很低,仅MTD处理就能占用大量的时间资源,导致后续留给参数估计的计算时间很有限。而一些在FPGA上实现MTD的方法只能做到固定点数,与串行处理器相比又少了灵活性。本文针对这些不足做出了一些改进,利用DDR3存储器在FPGA上实现了点数可变的快速MTD处理。具体时序操作由设计有限状态机来完成。其信号流向如图11所示。
|
Download:
|
| 图 11 FPGA实现MTD的信号流向 | |
做MTD处理就需要先缓存一个相干处理间隔(coherent process interval,CPI)的回波数据。为实现大量数据的缓存以及突破速度瓶颈。本文选择利用外挂的DDR3存储器来实现MTD处理。其具有容量大、时钟效率高等优势。本文所述雷达系统的FPGA外挂了容量为2 GB的DDR3内存条,最多能缓存近3 min的回波数据,能够实现MTD处理的要求。
FPGA对DDR3存储器的读写由Xilinx的存储器接口生成器(memory interface generator,MIG) IP核来实现,由于DDR3的读写方式有突发长度的限制,一次需要连续写入或读出8个地址中的数据。所以对应到用户接口时的数据位宽就是DDR3实际位宽的8倍。本文的设计中MTI后的数据I路和Q路各32位,总共64位。对应到DDR3的用户接口的数据位宽就变成了512位,位宽和时钟域的转换同样可以通过双端口RAM来实现。位宽转换后,只需要一个DDR3用户层时钟就能将8个距离采样点的数据写入存储器。若用户层时钟为100 MHz,即相当于实现了数据以800 MHz的速率进行存储,远超FPGA的片内存储器。本文即通过这种方式实现了数据的加速处理。
读取数据和写入时一致,一次读出8个有效数据。不同的是需要按照同一个距离维采样点读出数据。Xilinx的FFT IP核支持多通道FFT且点数可实时配置。在FFT处理前还需要加窗以减少旁瓣幅度。为充分利用FPGA并行处理的优势,本文将FFT核配置为8通道定点FFT。数据从DDR3中被读出后从加窗到FFT采用全流水并行操作的方式,获得远超于DSP处理的速度和吞吐率。在实现点数可变的处理方面,FPGA需要从DSP得到后续信号处理所需的最佳MTD点数,在下一个CPI开始前配置FFT的点数,修改只读存储器(read only memory,ROM)汉明窗表的寻址步长,进而实现窗函数和FFT运算根据点数实时更新。定点数在经过FFT后的数据位宽会变大,若截位处理又会损失一部分精度和动态范围。所以本文在FFT后将大位宽的定点数转成32位单精度浮点数,再通过高速SRIO接口将结果给DSP做后续处理。
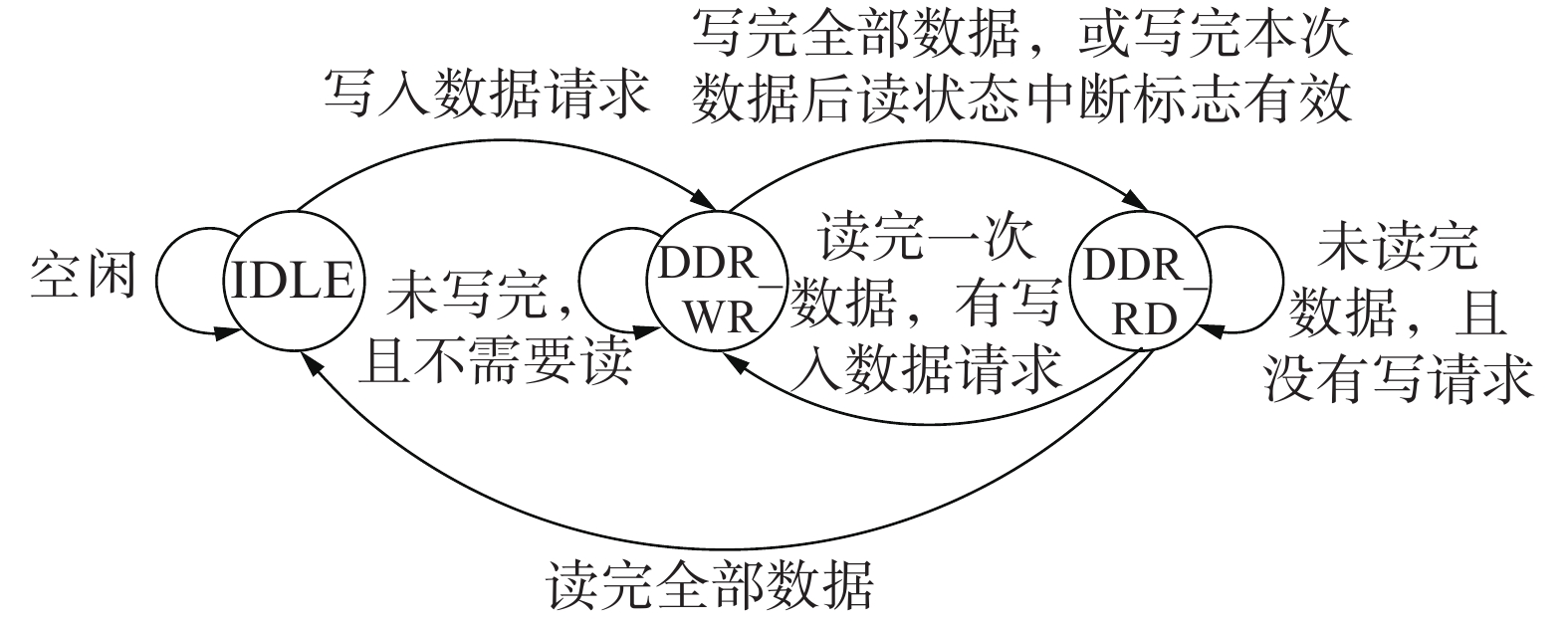
在一些脉冲重复时间(pulse repetition time,PRT)较小的场景,FPGA无法在一个PRT内完成所有回波的MTD处理。此时DDR3会产生读写冲突。传统的解决思路是用2片DDR3内存条实现乒乓缓存来获得时间差。但这样会造成存储资源的浪费,1片DDR3完全能够缓存2个CPI的回波数据。本文为了优化这个问题,利用了DDR3的块、行、列存储结构,将同一片DDR3中的2个块作为乒乓缓存的2个存储区。对于读写的总线冲突问题,本文在设计中加入了写请求中断的机制。由于数据写入是猝发的,本身不会持续很长时间,所以在读数据的同时若接到写请求,状态机会在读完这一次数据后跳到写数据的状态中,先将此次数据缓存到DDR3后,再继续执行读上一个CPI数据的操作。MTD处理的有限状态机状态转换如图12所示。
|
Download:
|
| 图 12 MTD处理状态转换 | |
将2.2节MTI处理后的数据输入到MTD模块在ModelSim进行仿真。为节省仿真时间,MTD点数取32,得到的结果如图13所示。

|
Download:
|
| 图 13 DDR3读写时序仿真 | |
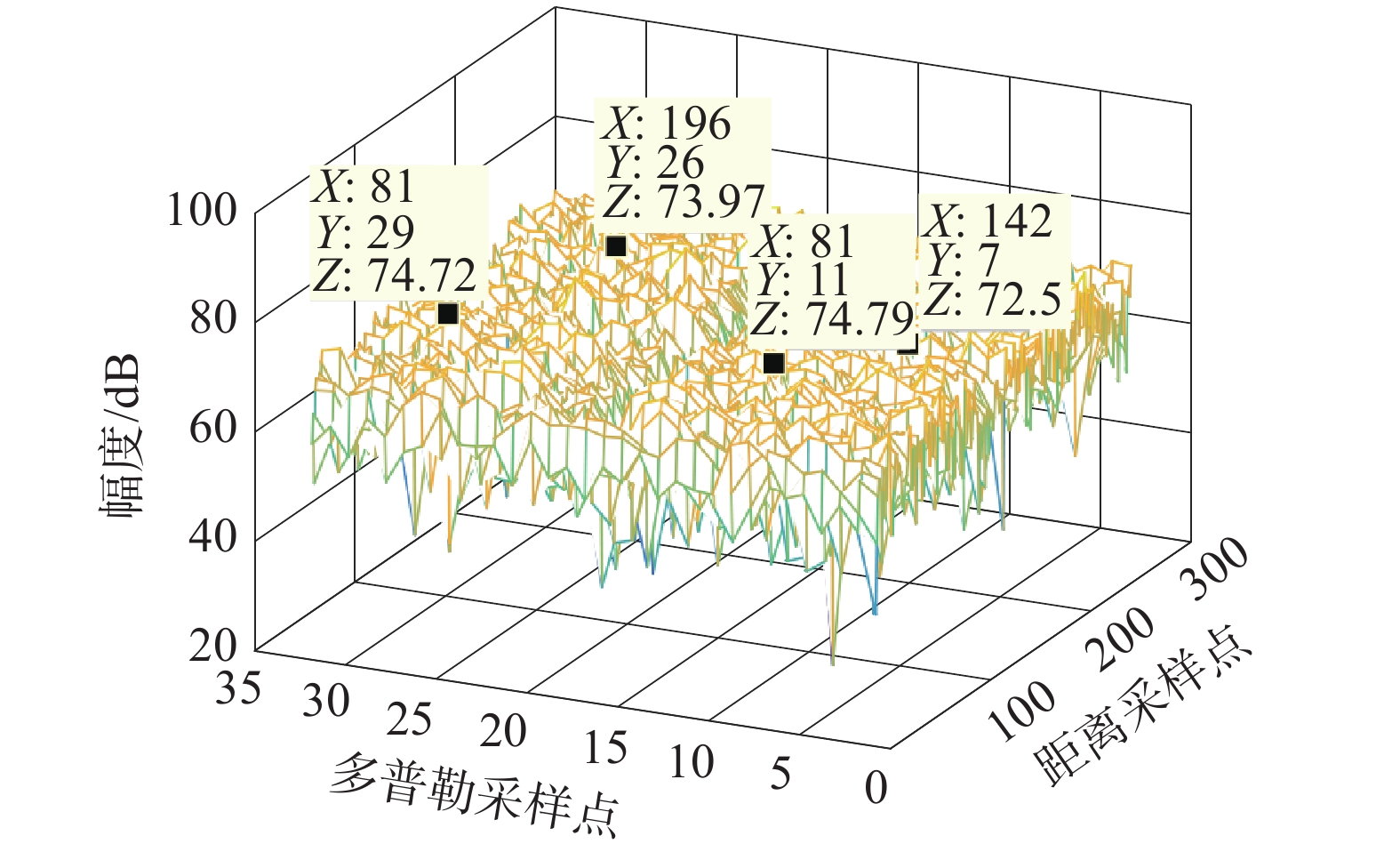
从时序仿真中能够看到,在状态机刚刚进行完一次读操作时,写请求(ddr_flag)到达。状态机则控制数据写入到DDR3的另一个块内(2个块首地址分别为0x00开头和0x02开头,从图11中可以看出)。对MTD仿真进行时钟计数,得到FPGA对三通道128周期(上下扫频各64周期)的数据进行MTD处理的时间为1.54 ms。将仿真后的结果保存为txt文件,在Matlab中画出32点上扫频MTD结果如图14所示。
|
Download:
|
| 图 14 ModelSim仿真的32点MTD结果 | |
从仿真结果可以看出本应在多普勒零频处的杂波已经被滤除干净,且通带较为平坦。证明了本文改进的MTI、MTD实现方法的正确性和有效性。
3 实测数据分析为模拟强杂波场景,测试在室内进行。先将无人机放在静止的平台上,仅安装一个旋翼。用遥控器控制其旋翼转动,观察旋翼速度对其多普勒特征的影响。根据文献[3]的结果,对于无人机目标来说,1个CPI最好不超过0.2 s。因此在测试时将MTD点数确定为64,即一个CPI的时间为0.128 s。MTI滤波器反馈支路的系数选为0.8。FPGA计算得到的处理结果可从DSP端通过仿真器读取到PC机上,图15为不同情况下的FPGA处理结果。

|
Download:
|
| 图 15 单旋翼不同转速FPGA的处理结果 | |
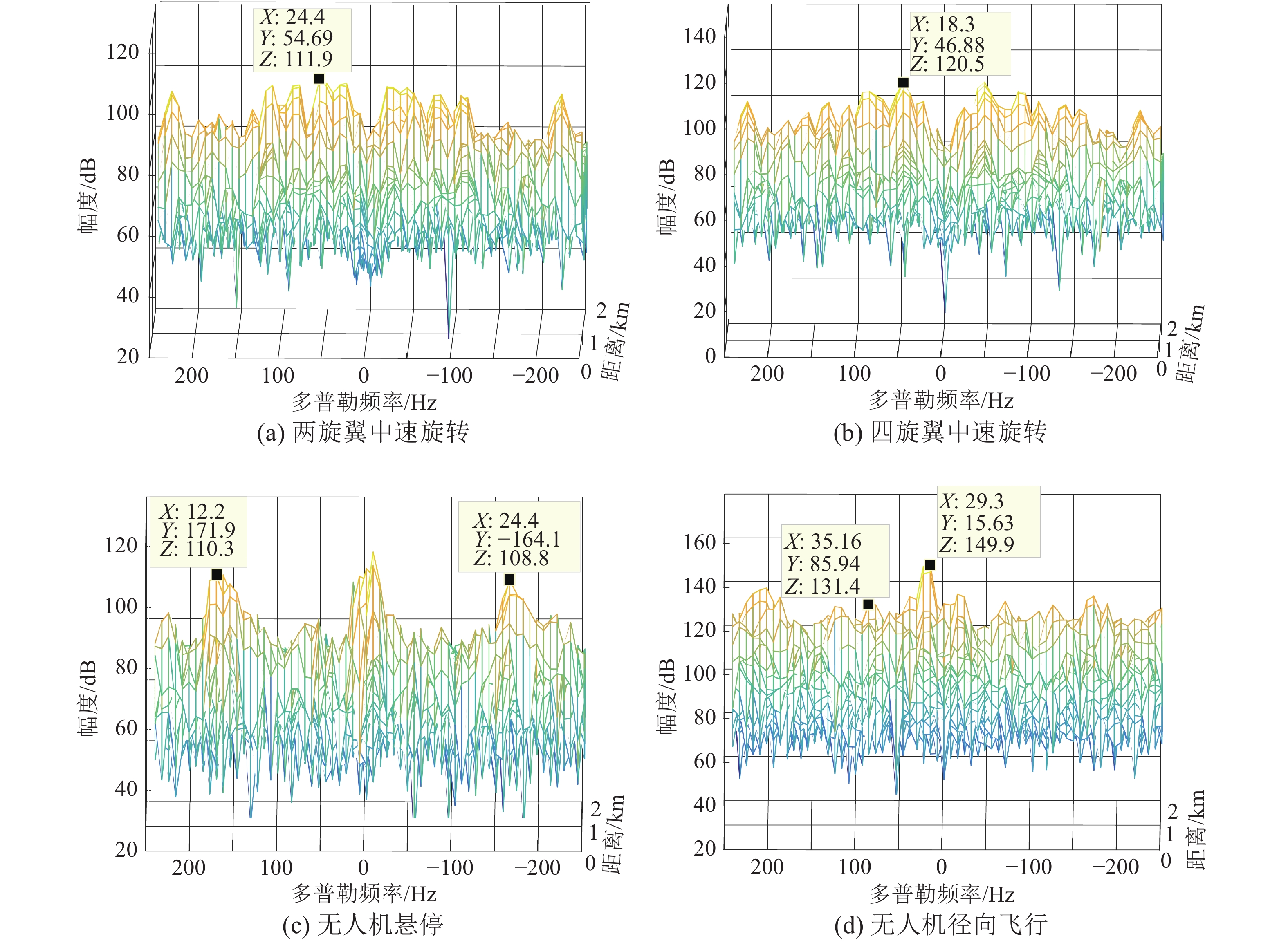
作为对比,图15(a)为无人机旋翼不旋转时FPGA的处理结果,即纯杂波的处理结果。可以看到R-D谱中无明显峰值,背景幅度大约75 dB。图15(b)、(c),(d)分别为无人机旋翼正常转速、慢速、快速的处理结果。可以发现旋翼的多普勒特征与仿真类似,为关于零频对称的谱线。慢速旋转时谱峰间隔变小,快速旋转时谱峰间隔变大。但由于室内环境封闭,系统受多径影响较大,造成能量峰值处的距离比实际距离远。且系统PRT较大,造成多普勒模糊,使得R-D谱除了明显的峰值以外还存在一些离散的谱线。为了分析不同旋翼数目和无人机不同运动状态的影响,本文又对比了两旋翼和四旋翼的情况以及无人机空中悬停和径向飞行的情况,结果如图16所示。
|
Download:
|
| 图 16 无人机不同旋翼数目和飞行状态的测试结果 | |
两旋翼与四旋翼的转速与图15(b)中单旋翼中速旋转的转速一致,可以看到旋翼数目增加后,离散的谱峰变得不再明显。此时旋翼的多普勒频率已经发生了很大的展宽,几个旋翼的谱峰混合在了一起。造成这种现象的原因有2个:一是由于旋翼的角度有差异,即便实际转速相同,投影到雷达径向的速度分量也会存在差异;二是雷达系统PRT过大导致多普勒无模糊范围较小,造成旋翼多普勒维信息的混叠。文献[12]也对这种现象进行了分析。
对比图16(c)和图16(d),无人机悬停时本身不运动,但由于气流扰动,实际上还是存在微小的位移。由于MTI滤波器的凹口较小,导致一部分无人机主体的信息还是被保留了下来。旋翼信息方面,无人机悬停时的旋翼转速要比静止在平台上时大,故距离零频最近的峰值所对应的多普勒频率也更大。而无人机在径向运动时,其主体也有了速度,多普勒频率位于MTI滤波器的通带范围内。所以可以看到图16(d)的目标峰值要比前面的旋翼以及悬停时的无人机主体能量要大得多。但运动的无人机旋翼转速也要比静止和悬停时大得多,故产生的多普勒模糊就更为严重。
4 结论1)从实际测试和仿真的结果能够看到本文的方法利用FPGA的并行处理优势。通过流水线处理和乒乓操作以及DDR3存储器的一些独特优势,实现了对地杂波的抑制、对目标回波的相参积累和微多普勒信息显示。一定程度上提高了系统的吞吐率,也缓解了DSP的资源压力。实测的旋翼多普勒特征也接近理论分析的结果,进一步证实了用FPGA实时处理的可行性。
2)目前关于无人机检测和识别的研究多在算法以及性能仿真上,少有立足于实际的雷达系统和硬件平台上的研究。本文对传统的MTI、MTD硬件实现方法做出了一些速度和吞吐率上的优化,目的是要在实际的系统上实现对无人机目标的回波特征,尤其是微多普勒特征的有效、快速和实时的提取,为雷达系统快速发现和识别无人机提供了一种思路。
3)从运动无人机的处理结果也可以看到,受硬件平台参数所限,系统的多普勒无模糊测量范围很小,无人机速度过快时会发生多普勒域的混叠。要解决这个问题可以适当减小PRT以获得更大的多普勒频率测量范围、更大的积累周期以及多普勒分辨力;也可以增大扫频带宽获得更小的距离分辨力,进一步优化R-D谱的精度,得到精确的旋翼参数估计结果。
| [1] |
何昌见, 凌建寿, 石凌飞. 无人机探测与反制技术现状及发展[J]. 警察技术, 2019(3): 4-7. ( 0) 0)
|
| [2] |
宋晨, 周良将, 吴一戎, 等. 基于自相关-倒谱联合分析的无人机旋翼转动频率估计方法[J]. 电子与信息学报, 2019, 41(2): 255-261. DOI:10.11999/JEIT180399 ( 0) 0)
|
| [3] |
HARMAN S. Analysis of the radar return of micro-UAVs in flight[C]//2017 IEEE Radar Conference. Seattle, USA, 2017: 1159–1164.
( 0) 0)
|
| [4] |
CHEN V C. 雷达中的微多普勒效应[M]. 吴顺君, 杜兰, 刘宏伟, 译. 北京: 电子工业出版社, 2013: 1-276.
( 0) 0)
|
| [5] |
SINGH A K, KIM Y H. Automatic measurement of blade length and rotation rate of drone using W-band micro-Doppler radar[J]. IEEE sensors journal, 2018, 18(5): 1895-1902. DOI:10.1109/JSEN.2017.2785335 ( 0) 0)
|
| [6] |
HARMAN S. Characteristics of the Radar signature of multi-rotor UAVs[C]//2016 European Radar Conference. London, UK, 2016: 93–96.
( 0) 0)
|
| [7] |
马娇, 董勇伟, 李原, 等. 多旋翼无人机微多普勒特性分析与特征提取[J]. 中国科学院大学学报, 2019, 36(2): 235-243. ( 0) 0)
|
| [8] |
涂亮. 多旋翼无人机雷达特征分析[D]. 南昌: 南昌大学, 2018: 1-67.
( 0) 0)
|
| [9] |
方鑫. 小型无人机目标雷达探测关键技术研究[D]. 成都: 电子科技大学, 2019: 1-113.
( 0) 0)
|
| [10] |
王琳琳. 宽带雷达无人机目标的微动特征提取及检测[D]. 哈尔滨: 哈尔滨工业大学, 2019: 1-57.
( 0) 0)
|
| [11] |
刘宇. 毫米波LFMCW雷达对地探测杂波抑制及恒虚警技术研究[D]. 南京: 南京理工大学, 2017: 1-69.
( 0) 0)
|
| [12] |
卜子容. 基于微多普勒特性的无人机目标检测与参数估计方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2019: 1-60.
( 0) 0)
|
 2021, Vol. 48
2021, Vol. 48


