多站无源定位技术在雷达、导航、无线通信等领域存在着广泛的应用^[1-3]。常用定位参数主要包括到达角度(angle of arrival，AOA)、到达时间差(time different of arrival，TDOA)、到达频率差(frequency different of arrival，FDOA)等。其中多站时差定位体制通过多个观测站测量辐射源信号到达各站的时间差实现辐射源定位，其定位成本低、定位精度较高并且不需要精确已知辐射源发射信号信息，是一种实时定位体制，因此受到广泛关注。

目前典型的TDOA定位算法包括Chan算法^[4-5]、迭代算法^[6]以及凸优化算法^[7]等。Chan算法通过信号到达两站的时差确定以两观测站为焦点的双曲面，多个双曲面的交点即为辐射源位置，该方法在测量误差较小时能够得到辐射源位置的解析解；但测量误差增大会使双曲面平移，会出现定位模糊或无解的问题，影响算法定位精度。迭代算法需要一个初始位置点进行迭代求解，若初始点与真实位置误差较大，算法往往不能收敛。凸优化算法具有局部最优点即全局最优点的特点^[8-9]，其首先利用中间变量构造伪线性方程并构造目标函数；然后在此基础上对目标函数进行松弛变换，将非线性的时差定位方程变换为一个凸优化问题，该方法具有良好的收敛特性，不会出现局部收敛或发散的现象。由于时差定位通常是在观测站位置信息精确已知的条件下进行，所以会受到使用条件的限制，当观测站为无人机或高速飞行器等运动平台时，其导航自定位存在误差，位置误差的存在会使时差定位算法的定位精度下降^[10-12]。因此，定位算法需要考虑位置误差对定位精度的影响。

本文考虑在观测站存在位置误差的条件下，提出了一种基于凸优化的时差定位算法，并通过仿真本文算法在不同的时差测量误差、位置误差条件下的定位误差，验证了算法的有效性；通过卡尔曼滤波处理多次定位结果进一步提升了辐射源定位精度。

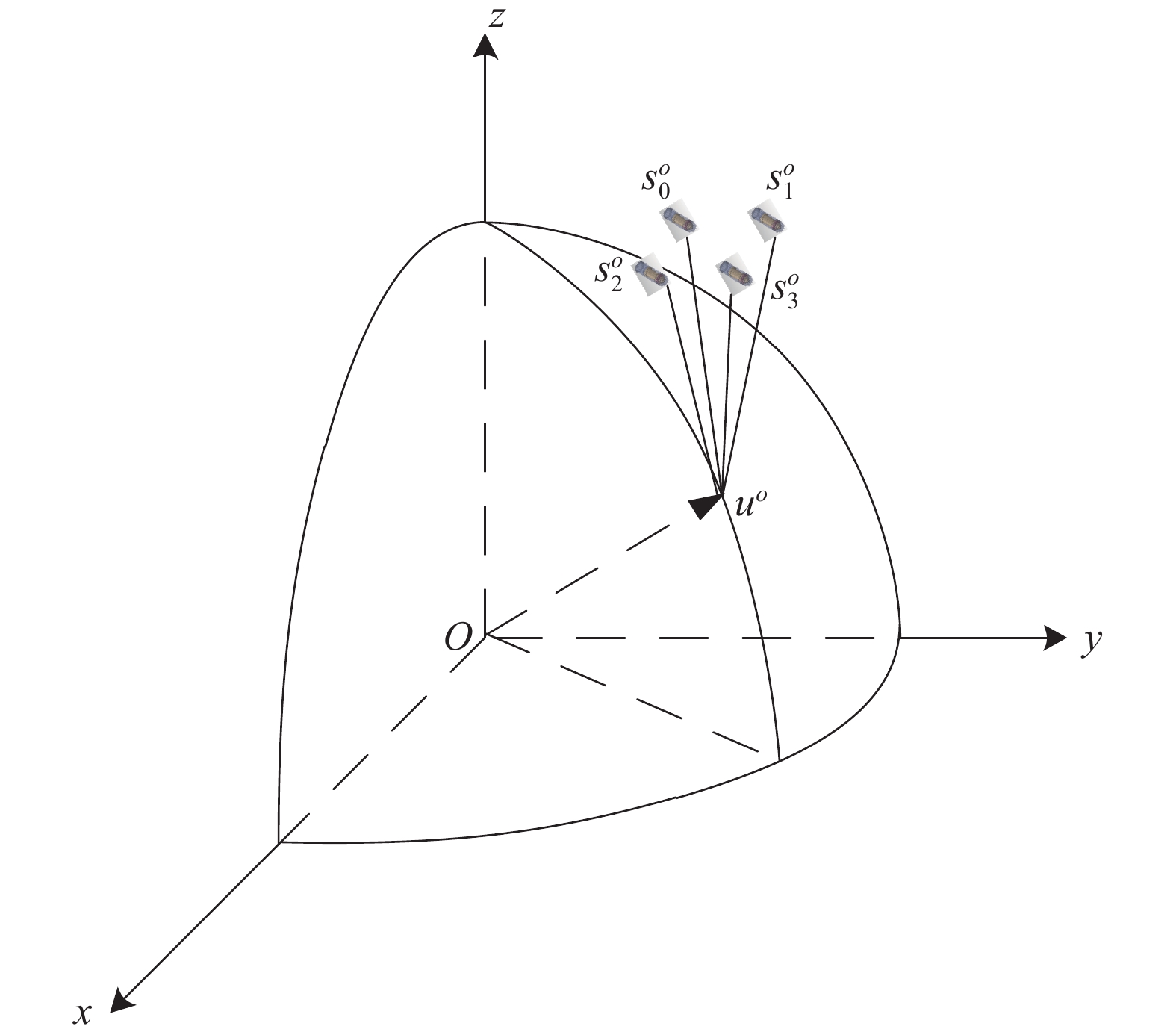
1 时差定位模型

如图1所示，假设在三维空间中位于地球表面的辐射源真实位置为 ${{{\mathit{\boldsymbol{u}}}}^o} = {[{x^o},{y^o},{z^o}]^{\rm{T}}}$ ，四站时差定位系统中各站真实位置分别为 ${{\mathit{\boldsymbol{s}}}}_i^o = {[x_i^o,y_i^o,z_i^o]^{\rm{T}}}$ ， $i = 1, $ $ 2,3 ,4$ 。

由于观测站存在位置误差，实际测量得到的观测站位置为 ${{{\mathit{\boldsymbol{s}}}}_i} = {{\mathit{\boldsymbol{s}}}}_i^o + \Delta {{{\mathit{\boldsymbol{s}}}}_i}$ ，写成矢量形式为

${{\mathit{\boldsymbol{s}}}} = {{{\mathit{\boldsymbol{s}}}}^o} + \Delta {{\mathit{\boldsymbol{s}}}}$

式中： ${{\mathit{\boldsymbol{s}}}} = {[{{{\mathit{\boldsymbol{s}}}}_1},{{{\mathit{\boldsymbol{s}}}}_2}, \cdots ,{{{\mathit{\boldsymbol{s}}}}_4}]^{\rm{T}}}$ ； ${{{\mathit{\boldsymbol{s}}}}^o} = {[{{\mathit{\boldsymbol{s}}}}_1^o,{{\mathit{\boldsymbol{s}}}}_2^o, \cdots ,{{\mathit{\boldsymbol{s}}}}_4^o]^{\rm{T}}}$ ，上标符号“ $o$ ”表示真实值； $\Delta {{\mathit{\boldsymbol{s}}}} = {[\Delta {{\mathit{\boldsymbol{s}}}}_1^{},\Delta {{\mathit{\boldsymbol{s}}}}_2^{}, \cdots ,\Delta {{\mathit{\boldsymbol{s}}}}_4^{}]^{\rm{T}}}$ 表示各站位置坐标的绝对误差，误差服从零均值高斯分布，其标准差为 ${\sigma _s}$ 。

以第一个观测站为主站，其余为辅站。多站之间采用中心授时法完成时钟同步，主辅站上分别携带有卫星导航接收机，根据卫星导航授时中心的中心授时调整自身时钟来达到相互之间的时钟同步。假设辐射源信号传输过程中不存在多径效应等问题，主辅站截获辐射源信号，通过脉冲配对和信号到达时间估计后得到3个测量时差，乘以电磁波传播速度 $c$ 得到时差的等价观测量即为距离差测量值：

$ \begin{array}{l} \;\;\;\;\;\;{{{\mathit{\boldsymbol{r}}}}_{i1}} = c\Delta {{{\mathit{\boldsymbol{t}}}}_{i1}} = {{\mathit{\boldsymbol{r}}}}_{i1}^o + \Delta {{\mathit{\boldsymbol{r}}}}\\ {{\mathit{\boldsymbol{r}}}}_{i1}^o = {{\mathit{\boldsymbol{r}}}}_i^o - {{\mathit{\boldsymbol{r}}}}_1^o = \left\| {{{{\mathit{\boldsymbol{u}}}}^o} - {{\mathit{\boldsymbol{s}}}}_i^o} \right\| - \left\| {{{{\mathit{\boldsymbol{u}}}}^o} - {{\mathit{\boldsymbol{s}}}}_1^o} \right\| \end{array}$

式中： ${{{\mathit{\boldsymbol{r}}}}_{i1}} = {[{{{\mathit{\boldsymbol{r}}}}_{21}},{{{\mathit{\boldsymbol{r}}}}_{31}},{{{\mathit{\boldsymbol{r}}}}_{41}}]^{\rm{T}}}$ 为距离差测量值； ${{\mathit{\boldsymbol{r}}}}_{i1}^o = [{{\mathit{\boldsymbol{r}}}}_{21}^o, {{\mathit{\boldsymbol{r}}}}_{31}^o, $ $ {{\mathit{\boldsymbol{r}}}}_{41}^o]^{\rm{T}}$ 为距离差真实值； $\Delta {{\mathit{\boldsymbol{r}}}} = c\Delta {{\mathit{\boldsymbol{t}}}}$ ； $\Delta {{\mathit{\boldsymbol{t}}}}$ 为时差测量误差，服从零均值高斯分布，标准差为 ${\sigma _t}$ 。假设时差测量误差与位置误差不相关。

本算法对地球表面高程为零的静止辐射源进行定位，利用这一信息作为辐射源位置求解的约束条件，采用WGS-84地球椭球模型^[13]。在WGS-84模型下，辐射源的空间直角坐标与经纬高坐标的关系为

$\left\{ \begin{array}{l} x = (N + H)\cos B\cos L \\ y = (N + H)\cos B\sin L \\ z = [N(1 - {e^2}) + H]\sin B \end{array} \right.$

式中： $N = {a / {\sqrt {1 - {e^2}{{\sin }^2}B} }}$ 为辐射源所在位置的卯酉圈曲率半径；a = 6 378 137 m为地球长半轴； ${e^2}$ 为第一偏心率。则约束条件为

$\frac{{{x^2}}}{{{{(N + H)}^2}}} + \frac{{{y^2}}}{{{{(N + H)}^2}}} + \frac{{{z^2}}}{{{{[N(1 - {e^2}) + H]}^2}}} = 1$

式中： $H$ 为辐射源高度信息，对位于地球表面的辐射源，其高度 $H = 0$ 。存在约束条件时的多站时差定位方程如下：

$\left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{r}}}}_{21}^o = {{\mathit{\boldsymbol{r}}}}_i^o - {{\mathit{\boldsymbol{r}}}}_1^o = \left\| {{{{\mathit{\boldsymbol{u}}}}^o} - {{\mathit{\boldsymbol{s}}}}_2^o} \right\| - \left\| {{{{\mathit{\boldsymbol{u}}}}^o} - {{\mathit{\boldsymbol{s}}}}_1^o} \right\|} \\ \quad\quad\quad\quad\quad\quad\quad\vdots \\ {{{\mathit{\boldsymbol{r}}}}_{i1}^o = {{\mathit{\boldsymbol{r}}}}_i^o - {{\mathit{\boldsymbol{r}}}}_1^o = \left\| {{{{\mathit{\boldsymbol{u}}}}^o} - {{\mathit{\boldsymbol{s}}}}_i^o} \right\| - \left\| {{{{\mathit{\boldsymbol{u}}}}^o} - {{\mathit{\boldsymbol{s}}}}_1^o} \right\|} \\ {\dfrac{{{x^2}}}{{{{(N + H)}^2}}} + \dfrac{{{y^2}}}{{{{(N + H)}^2}}} + \dfrac{{{z^2}}}{{{{[N(1 - {e^2}) + H]}^2}}} = 1} \end{array}} \right.$

2 基于凸优化的时差定位算法

首先将非线性的时差定位方程伪线性化。将主站与辐射源的距离 ${{\mathit{\boldsymbol{r}}}}_1^o$ 作为辅助变量，对 ${{\mathit{\boldsymbol{r}}}}_i^o = {{\mathit{\boldsymbol{r}}}}_{i1}^o + $ $ {{\mathit{\boldsymbol{r}}}}_1^o$ 两边进行平方，并将含有误差的 ${{\mathit{\boldsymbol{r}}}}_{i1}^{}$ 和 ${{{\mathit{\boldsymbol{s}}}}_i}$ 代入方程并作泰勒级数展开后得到关于辐射源位置 ${{{\mathit{\boldsymbol{u}}}}^o}$ 和辅助变量 ${\hat{{\mathit{\boldsymbol{r}}}}}_1^o$ 的伪线性方程：

$ \begin{array}{c} {\eta _i} = {{\mathit{\boldsymbol{r}}}}_{i1}^2 - {{\mathit{\boldsymbol{s}}}}_i^{\rm{T}}{{{\mathit{\boldsymbol{s}}}}_i} + {{\mathit{\boldsymbol{s}}}}_1^{\rm{T}}{{{\mathit{\boldsymbol{s}}}}_1} + 2{({{{\mathit{\boldsymbol{s}}}}_i} - {{{\mathit{\boldsymbol{s}}}}_1})^{\rm{T}}}{{{\mathit{\boldsymbol{u}}}}^o} + 2{\hat{{\mathit{\boldsymbol{r}}}}}_1^o{{{\mathit{\boldsymbol{r}}}}_{i1}} =\\ 2{{\mathit{\boldsymbol{r}}}}_i^o\Delta {{{\mathit{\boldsymbol{r}}}}_{i1}} + 2{({{{\mathit{\boldsymbol{u}}}}^o} - {{{\mathit{\boldsymbol{s}}}}_i})^{\rm{T}}}\Delta {{{\mathit{\boldsymbol{s}}}}_i} - 2[{({{{\mathit{\boldsymbol{u}}}}^o} - {{{\mathit{\boldsymbol{s}}}}_1})^{\rm{T}}} + {{{\mathit{\boldsymbol{r}}}}_{i1}}\rho _{{{{\mathit{\boldsymbol{u}}}}^o},{{{\mathit{\boldsymbol{s}}}}_1}}^{\rm{T}}]\Delta {{{\mathit{\boldsymbol{s}}}}_1} \end{array} $

式中 $\rho _{{{{\mathit{\boldsymbol{u}}}}^o},{{{\mathit{\boldsymbol{s}}}}_1}}^{} = ({{{\mathit{\boldsymbol{u}}}}^o} - {{{\mathit{\boldsymbol{s}}}}_i})/\left\| {{{{\mathit{\boldsymbol{u}}}}^o} - {{{\mathit{\boldsymbol{s}}}}_i}} \right\|$ 。定义辐射源位置和辅助变量的矢量形式为 ${{\mathit{\boldsymbol{y}}}} = {[{{{\mathit{\boldsymbol{u}}}}^o}^{\rm{T}},{\hat{{\mathit{\boldsymbol{r}}}}}_1^o]^{\rm{T}}}$ ，则：

$ {{\mathit{\boldsymbol{\eta}}}} = {{\mathit{\boldsymbol{h}}}} - {{\mathit{\boldsymbol{Gy}}}} = {{\mathit{\boldsymbol{B}}}}\Delta {{\mathit{\boldsymbol{r}}}} + {{\mathit{\boldsymbol{D}}}}\Delta {{\mathit{\boldsymbol{s}}}} $

(1)

$ \begin{array}{c} {{\mathit{\boldsymbol{h}}}} = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{r}}}}_{21}^2 - {{\mathit{\boldsymbol{s}}}}_2^{\rm{T}}{{{\mathit{\boldsymbol{s}}}}_2} + {{\mathit{\boldsymbol{s}}}}_1^{\rm{T}}{{{\mathit{\boldsymbol{s}}}}_1}} \\ {{{\mathit{\boldsymbol{r}}}}_{31}^2 - {{\mathit{\boldsymbol{s}}}}_3^{\rm{T}}{{{\mathit{\boldsymbol{s}}}}_3} + {{\mathit{\boldsymbol{s}}}}_1^{\rm{T}}{{{\mathit{\boldsymbol{s}}}}_1}} \\ {{{\mathit{\boldsymbol{r}}}}_{41}^2 - {{\mathit{\boldsymbol{s}}}}_4^{\rm{T}}{{{\mathit{\boldsymbol{s}}}}_4} + {{\mathit{\boldsymbol{s}}}}_1^{\rm{T}}{{{\mathit{\boldsymbol{s}}}}_1}} \end{array}} \right]\\ {{\mathit{\boldsymbol{G}}}} = \left[ {\begin{array}{*{20}{c}} {{{({{{\mathit{\boldsymbol{s}}}}_2} - {{{\mathit{\boldsymbol{s}}}}_1})}^{\rm{T}}}}&{{{\mathit{\boldsymbol{r}}}}_{21}^{}} \\ {{{({{{\mathit{\boldsymbol{s}}}}_3} - {{{\mathit{\boldsymbol{s}}}}_1})}^{\rm{T}}}}&{{{\mathit{\boldsymbol{r}}}}_{31}^{}} \\ {{{({{{\mathit{\boldsymbol{s}}}}_4} - {{{\mathit{\boldsymbol{s}}}}_1})}^{\rm{T}}}}&{{{\mathit{\boldsymbol{r}}}}_{41}^{}} \end{array}} \right]\\ {{\mathit{\boldsymbol{B}}}} = 2\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{r}}}}_2^o}&0&0 \\ 0&{{{\mathit{\boldsymbol{r}}}}_3^o}&0 \\ 0&0&{{{\mathit{\boldsymbol{r}}}}_4^o} \end{array}} \right]\\ {{\mathit{\boldsymbol{D}}}} = 2\left[{\begin{array}{*{20}{c}} { - {{({{{\mathit{\boldsymbol{u}}}}^o} - {{{\mathit{\boldsymbol{s}}}}_1})}^{\rm{T}}} - {{{\mathit{\boldsymbol{r}}}}_{21}}{{\mathit{\boldsymbol{\rho }}}}_{{{{\mathit{\boldsymbol{u}}}}^o},{{{\mathit{\boldsymbol{s}}}}_1}}^{\rm{T}}}&{{{({{{\mathit{\boldsymbol{u}}}}^o} - {{{\mathit{\boldsymbol{s}}}}_2})}^{\rm{T}}}}&{{{{\mathit{\boldsymbol{0}}}}^{\rm{T}}}}&{{{{\mathit{\boldsymbol{0}}}}^{\rm{T}}}} \\ { - {{({{{\mathit{\boldsymbol{u}}}}^o} - {{{\mathit{\boldsymbol{s}}}}_1})}^{\rm{T}}} - {{{\mathit{\boldsymbol{r}}}}_{21}}{{\mathit{\boldsymbol{\rho }}}}_{{{{\mathit{\boldsymbol{u}}}}^o},{{{\mathit{\boldsymbol{s}}}}_1}}^{\rm{T}}}&{{{{\mathit{\boldsymbol{0}}}}^{\rm{T}}}}&{{{({{{\mathit{\boldsymbol{u}}}}^o} - {{{\mathit{\boldsymbol{s}}}}_3})}^{\rm{T}}}}&{{{{\mathit{\boldsymbol{0}}}}^{\rm{T}}}} \\ { - {{({{{\mathit{\boldsymbol{u}}}}^o} - {{{\mathit{\boldsymbol{s}}}}_1})}^{\rm{T}}} - {{{\mathit{\boldsymbol{r}}}}_{21}}{{\mathit{\boldsymbol{\rho }}}}_{{{{\mathit{\boldsymbol{u}}}}^o},{{{\mathit{\boldsymbol{s}}}}_1}}^{\rm{T}}}&{{{{\mathit{\boldsymbol{0}}}}^{\rm{T}}}}&{{{{\mathit{\boldsymbol{0}}}}^{\rm{T}}}}&{{{({{{\mathit{\boldsymbol{u}}}}^o} - {{{\mathit{\boldsymbol{s}}}}_4})}^{\rm{T}}}} \end{array}}\right] \end{array} $

假设 ${{{\mathit{\boldsymbol{u}}}}^o}$ 与 ${\hat{{\mathit{\boldsymbol{r}}}}}_1^o$ 无关，将式(1)变为关于 ${{\mathit{\boldsymbol{y}}}}$ 的伪线性方程，对其进行加权最小二乘估计：

$ \hat \eta = \arg \min {({{\mathit{\boldsymbol{Gy}}}} - {{\mathit{\boldsymbol{h}}}})^{\rm{T}}}{{\mathit{\boldsymbol{W}}}}({{\mathit{\boldsymbol{Gy}}}} - {{\mathit{\boldsymbol{h}}}})= {({{{\mathit{\boldsymbol{G}}}}^{\rm{T}}}{{\mathit{\boldsymbol{WG}}}})^{{\rm{ - }}1}}{{{\mathit{\boldsymbol{G}}}}^{\rm{T}}}{{\mathit{\boldsymbol{Wh}}}} $

式中 ${{\mathit{\boldsymbol{W}}}}$ 为加权矩阵， ${{\mathit{\boldsymbol{W}}}} = {\rm{E}}{[{{\mathit{\boldsymbol{\eta}}}} {{{\mathit{\boldsymbol{\eta}}}} ^{\rm{T}}}]^{ - 1}} = ({{\mathit{\boldsymbol{B}}}}{{{\mathit{\boldsymbol{Q}}}}_r}{{{\mathit{\boldsymbol{B}}}}^{\rm{T}}}{\rm{ + }} {{\mathit{\boldsymbol{D}}}}{{{\mathit{\boldsymbol{Q}}}}_s}{{{\mathit{\boldsymbol{D}}}}^{\rm{T}}})^{ - 1}$ 。由于 ${{\mathit{\boldsymbol{W}}}}$ 式中辐射源位置是未知的，考虑各站到辐射源的距离远大于各站之间的基线距离，则可以假设各站与辐射源之间的距离近似相等，则 ${{\mathit{\boldsymbol{B}}}} = 2{{{\mathit{\boldsymbol{I}}}}_{3 \times 3}},{{\mathit{\boldsymbol{D}}}} = {{\mathit{\boldsymbol{2}}}}[ - {1_{3 \times 3}},{{{\mathit{\boldsymbol{I}}}}_{3 \times 3}}]$ 。

由于求解过程是在假设 ${{\mathit{\boldsymbol{y}}}}$ 中各分量相互独立的前提下进行的，事实上，它们受限于 ${{\mathit{\boldsymbol{r}}}}_1^o = $ $ \left\| {{{{\mathit{\boldsymbol{u}}}}^o} - {{\mathit{\boldsymbol{s}}}}_1^o} \right\|$ 。因此构造目标函数：

$\begin{array}{*{20}{c}} {\mathop {\min }\limits_{{\mathit{\boldsymbol{y}}}} {{({{\mathit{\boldsymbol{Gy}}}} - {{\mathit{\boldsymbol{h}}}})}^{\rm{T}}}{{\mathit{\boldsymbol{W}}}}({{\mathit{\boldsymbol{Gy}}}} - {{\mathit{\boldsymbol{h}}}})} \\ {{\rm{s}}.{\rm{t}}.\;\;{{\mathit{\boldsymbol{y}}}}(4) = \left\| {{{\mathit{\boldsymbol{y}}}}(1:3) - {{{\mathit{\boldsymbol{s}}}}_1}} \right\|} \end{array}$

该函数是非线性等式约束优化问题，其为一个非凸优化问题。对该问题可以通过松弛变换处理，将其转换为一个凸优化问题，利用凸优化局部最优点即为全局最优点的优点可以有效求解。根据矩阵迹的性质 ${{{\mathit{\boldsymbol{x}}}}^{\rm{T}}}{{\mathit{\boldsymbol{Ax}}}} = {\rm{tr}}({{{\mathit{\boldsymbol{x}}}}^{\rm{T}}}{{\mathit{\boldsymbol{Ax}}}}) = {\rm{tr}}({{\mathit{\boldsymbol{x}}}}{{{\mathit{\boldsymbol{x}}}}^{\rm{T}}}{{\mathit{\boldsymbol{A}}}})$ ，对目标函数进行变换：

${({{\mathit{\boldsymbol{Gy}}}} - {{\mathit{\boldsymbol{h}}}})^{\rm{T}}}{{\mathit{\boldsymbol{W}}}}({{\mathit{\boldsymbol{Gy}}}} - {{\mathit{\boldsymbol{h}}}}) = {\rm{tr}}\left\{ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Y}}}}&{{\mathit{\boldsymbol{y}}}} \\ {{{{\mathit{\boldsymbol{y}}}}^{\rm{T}}}}&1 \end{array}} \right]{{\mathit{\boldsymbol{F}}}}} \right\}$

其中 ${{\mathit{\boldsymbol{Y}}}} = {{\mathit{\boldsymbol{y}}}}{{{\mathit{\boldsymbol{y}}}}^{\rm{T}}}$ ， ${{\mathit{\boldsymbol{F}}}} = \left[ {\begin{array}{*{20}{c}} {{{{\mathit{\boldsymbol{G}}}}^{\rm{T}}}{{\mathit{\boldsymbol{WG}}}}}&{ - {{{\mathit{\boldsymbol{G}}}}^{\rm{T}}}{{\mathit{\boldsymbol{Wh}}}}} \\ { - {{{\mathit{\boldsymbol{h}}}}^{\rm{T}}}{{\mathit{\boldsymbol{WG}}}}}&{{{{\mathit{\boldsymbol{h}}}}^{\rm{T}}}{{\mathit{\boldsymbol{Wh}}}}} \end{array}} \right]$ 。则原问题等价为

$ \begin{array}{c} \mathop {\min }\limits_{{{\mathit{\boldsymbol{Y}}}},{{\mathit{\boldsymbol{y}}}}} \;{\rm{tr}}\left\{ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Y}}}}&{{\mathit{\boldsymbol{y}}}} \\ {{{{\mathit{\boldsymbol{y}}}}^{\rm{T}}}}&1 \end{array}} \right]{{\mathit{\boldsymbol{F}}}}} \right\} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;{{\mathit{\boldsymbol{Y}}}}(4,4){\rm{ = tr}}\{ {{\mathit{\boldsymbol{Y}}}}(1:3,1:3)\} - 2{{\mathit{\boldsymbol{s}}}}_1^{\rm{T}}{{\mathit{\boldsymbol{y}}}}(1:3) + {\left\| {{{{\mathit{\boldsymbol{s}}}}_1}} \right\|^2} \\ \;\;\;\;\;\;{{\mathit{\boldsymbol{Y}}}} = {{\mathit{\boldsymbol{y}}}}{{{\mathit{\boldsymbol{y}}}}^{\rm{T}}} \end{array} $

对于形如 ${{\mathit{\boldsymbol{Y}}}} = {{\mathit{\boldsymbol{y}}}}{{{\mathit{\boldsymbol{y}}}}^{\rm{T}}}$ 的矩阵等式有：

${{\mathit{\boldsymbol{Y}}}} = {{\mathit{\boldsymbol{y}}}}{{{\mathit{\boldsymbol{y}}}}^{\rm{T}}} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Y}}}}&{{\mathit{\boldsymbol{y}}}} \\ {{{{\mathit{\boldsymbol{y}}}}^{\rm{T}}}}&1 \end{array}} \right]\underline \succ 0} \\ {{\rm{rank(}}{{\mathit{\boldsymbol{Y}}}}{\rm{) = 1}}} \end{array}} \right.$

舍弃式中约束项 ${\rm{rank(}}{{\mathit{\boldsymbol{Y}}}}{\rm{) = 1}}$ ，将原问题进行松弛后得到一个凸优化问题，同时加入地球表面约束条件：

$ \begin{array}{c} \mathop {\min }\limits_{{{\mathit{\boldsymbol{Y}}}},{{\mathit{\boldsymbol{y}}}}} \;{\rm{tr}}\left\{ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Y}}}}&{{\mathit{\boldsymbol{y}}}} \\ {{{{\mathit{\boldsymbol{y}}}}^{\rm{T}}}}&1 \end{array}} \right]{{\mathit{\boldsymbol{F}}}}} \right\} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;{{\mathit{\boldsymbol{Y}}}}(4,4){\rm{ = tr}}\{ {{\mathit{\boldsymbol{Y}}}}(1:3,1:3)\} - 2{{\mathit{\boldsymbol{s}}}}_1^{\rm{T}}{{\mathit{\boldsymbol{y}}}}(1:3) + {\left\| {{{{\mathit{\boldsymbol{s}}}}_1}} \right\|^2} \\ \;\;\;\;\;\;\dfrac{{{{\mathit{\boldsymbol{Y}}}}(1,1)}}{{{{(N + H)}^2}}} + \dfrac{{{{\mathit{\boldsymbol{Y}}}}(2,2)}}{{{{(N + H)}^2}}} + \dfrac{{{{\mathit{\boldsymbol{Y}}}}(3,3)}}{{{{[N(1 - {e^2}) + H]}^2}}} = 1 \\ \;\;\;\;\;\;\;{{\mathit{\boldsymbol{Y}}}}(5,5) = 1 \end{array} $

该问题的求解已经成熟应用于MATLAB内嵌的CVX工具箱中，该方法可以在几十步之内以给定的精度求解凸优化问题^[9]，当结果满足门限时，求解结束并输出定位结果。根据 ${{\mathit{\boldsymbol{Y}}}}$ 的定义可得辐射源定位结果为

${\hat{{\mathit{\boldsymbol{u}}}}} = {\hat{{\mathit{\boldsymbol{y}}}}}(1:3) = (\hat x,\hat y,\hat z)$

综上所述，本算法基本流程为：

1)根据时差信息与观测站坐标构建时差定位方程；

2)对定位方程进行变换并结合地球表面约束条件，将其变为一个凸优化问题；

3)利用CVX工具箱求解，若结果满足给定门限，则求解结束，否则继续迭代并更新定位结果。

3 仿真分析 3.1 单次定位误差仿真

本文在不同时差测量误差和位置误差情况下仿真各种算法的定位误差。假设辐射源位置为 ${{{\mathit{\boldsymbol{u}}}}^o} = {[ - 1\;211.96,5\;790.91,2\;374.68]^{\rm{T}}}$ km，4个观测站采用一主三从模式，各站真实坐标为如表1所示。此时主站与辐射源之间的距离 $R$ 为71.50 km，考虑到定位精度与距离的关系，本文选取 $1{\rm{\% }}R$ 作为检测时差定位算法精度的标准。

本文中各种算法的定位精度用均方根误差(root mean square error，RMSE)来表示，其定义为 ${\rm{RMSE(}}{{\mathit{\boldsymbol{u}}}}) = \Bigg(\displaystyle\sum\limits_{l = 1}^L {{\left\| {{{{\mathit{\boldsymbol{u}}}}^l} - {{{\mathit{\boldsymbol{u}}}}^o}} \right\|}^2}\Bigg/ $ $ L \Bigg)^{1/2}$ ，其中 $L=100$ 为蒙特卡洛仿真次数， ${{{\mathit{\boldsymbol{u}}}}^l}$ 为第 $l$ 次蒙特卡洛仿真得到的位置估计值， ${{{\mathit{\boldsymbol{u}}}}^o}$ 为辐射源真实位置。

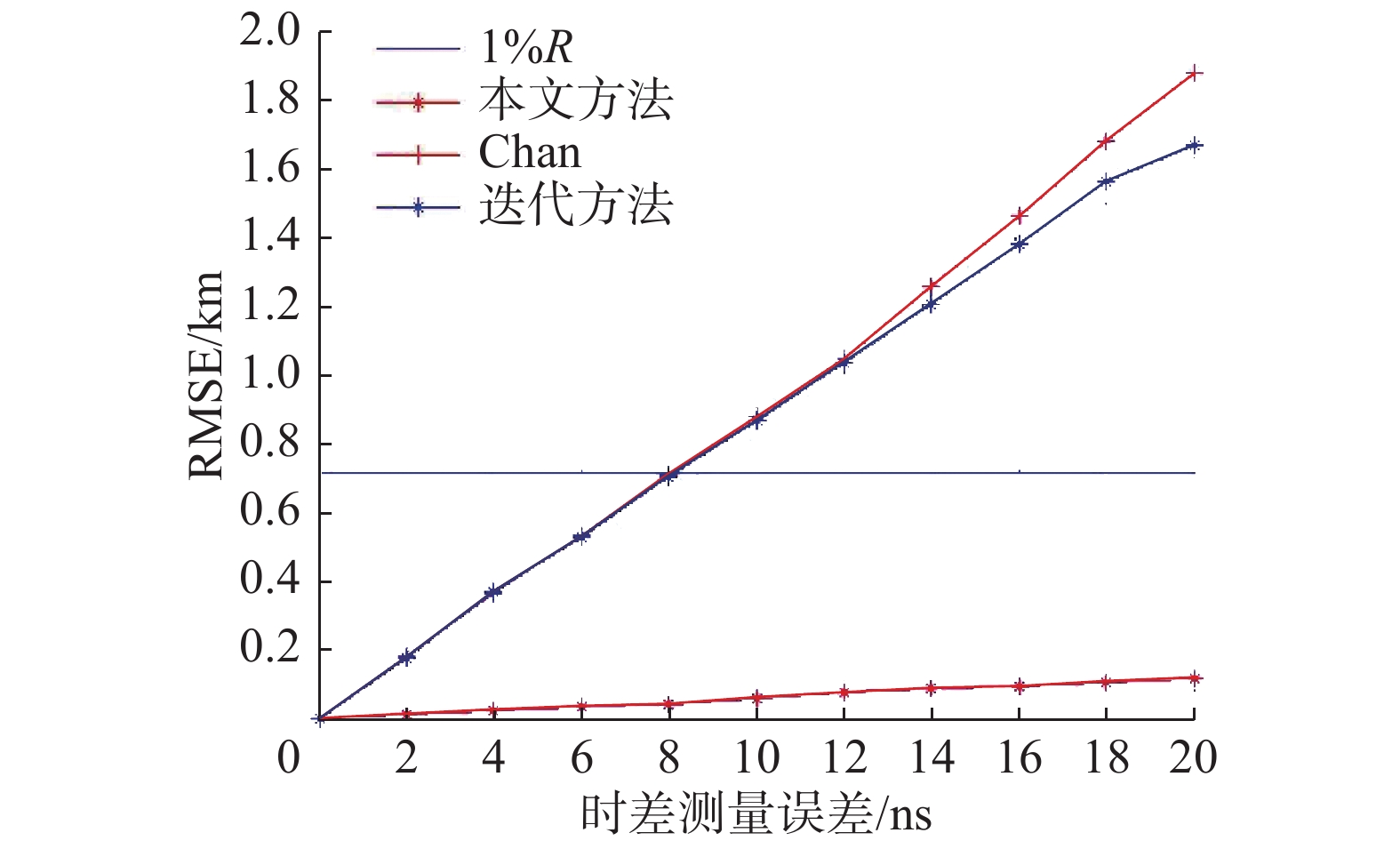
假设各站绝对位置误差 ${\sigma _s}$ 为0 m，图2表示了各种算法对辐射源的定位误差随时差测量误差变化情况，其中迭代算法初始值由Chan算法给出。从图中可以看出，当时差测量误差和位置误差均为零时，3种算法均能准确计算出辐射源位置，定位误差接近于零；当时差测量误差大于8 ns时，Chan算法和迭代算法的定位误差大于 $1{\text{%}}R$ ，不能满足高精度定位的要求；而本文算法在时差测量误差为20 ns时的定位误差为0.12 km，仍能满足 $1{\text{%}}R$ 的定位精度要求。

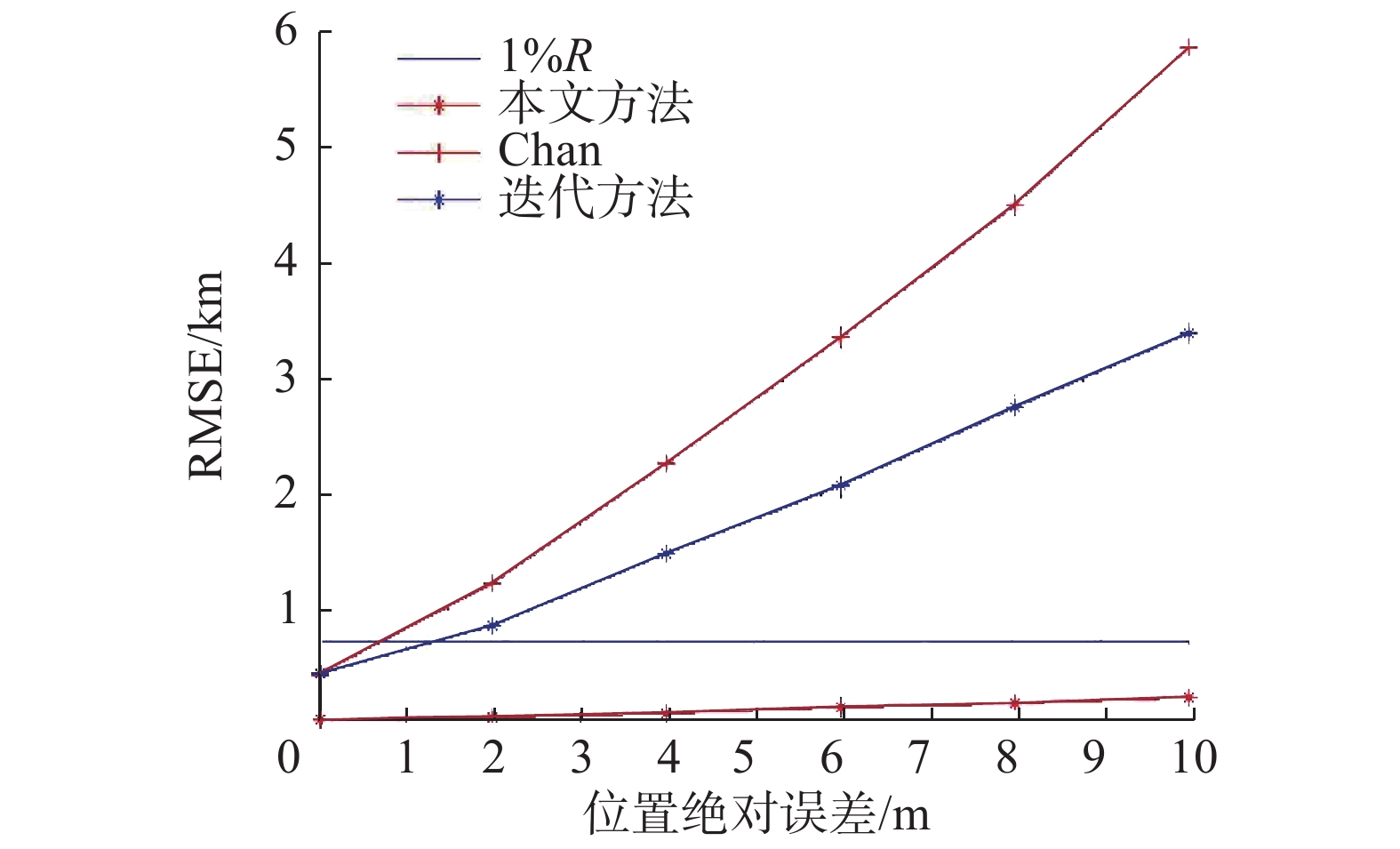
假设主从站时差测量误差 ${\sigma _t}$ 为5 ns，图3表示了各种算法对辐射源的定位误差随位置误差变化情况，其中迭代算法初始值由Chan算法给出。从图中可以看出，由于位置误差和时差测量误差的影响，当位置误差大于2 m时，Chan算法和迭代算法的定位误差大于 $1{\text{%}}R$ ；而本文算法在位置误差为10 m时的定位误差为0.21 km，仍能满足 $1{\text{%}}R$ 的高精度定位要求。

3.2 多次定位仿真

为了提升辐射源定位精度，可以对辐射源进行多次定位并对多次定位结果进行滤波处理^[14]。设辐射源为 ${{{\mathit{\boldsymbol{u}}}}_k} = {[{x_k},{y_k},{z_k}]^{\rm{T}}}$ ，其状态方程与测量方程为

$\begin{array}{*{20}{c}} {{{{\mathit{\boldsymbol{u}}}}_{k + 1}} = {{\mathit{\boldsymbol{\varPhi }}}}{{{\mathit{\boldsymbol{u}}}}_k}} \\ {{{{\mathit{\boldsymbol{Y}}}}_k} = {{{\mathit{\boldsymbol{H}}}}_k}{{{\mathit{\boldsymbol{X}}}}_k} + {{\mathit{\boldsymbol{n}}}}} \end{array}$

式中： ${{{\mathit{\boldsymbol{Y}}}}_k} = {({\hat x_k},{\hat y_k},{\hat z_k})^{\rm{T}}}$ 为第 $k$ 时刻辐射源位置测量值；由于辐射源是固定的，因此状态转移矩阵 ${{\mathit{\boldsymbol{\varPhi }}}}$ 与测量矩阵 ${{{\mathit{\boldsymbol{H}}}}_k}$ 均为 $3 \times 3$ 的单位矩阵； ${{{\mathit{\boldsymbol{n}}}}_k}$ 为辐射源定位误差，其协方差矩阵为^[9]

${{{\mathit{\boldsymbol{R}}}}_k} = \left[ {{{{\mathit{\boldsymbol{n}}}}_k}{{\mathit{\boldsymbol{n}}}}_k^{\rm{T}}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\delta }}}}_{\Delta {{{\mathit{\boldsymbol{r}}}}_1}}^2}&0&0 \\ 0&{{{\mathit{\boldsymbol{\delta }}}}_{\Delta {{{\mathit{\boldsymbol{r}}}}_2}}^2}&0 \\ 0&0&{{{\mathit{\boldsymbol{\delta }}}}_{\Delta {{{\mathit{\boldsymbol{r}}}}_3}}^2} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {2{{\mathit{\boldsymbol{\delta }}}}_{{\mathit{\boldsymbol{s}}}}^2}&{{{\mathit{\boldsymbol{\delta }}}}_{{\mathit{\boldsymbol{s}}}}^2}&{{{\mathit{\boldsymbol{\delta }}}}_{{\mathit{\boldsymbol{s}}}}^2} \\ {{{\mathit{\boldsymbol{\delta }}}}_{{\mathit{\boldsymbol{s}}}}^2}&{2{{\mathit{\boldsymbol{\delta }}}}_{{\mathit{\boldsymbol{s}}}}^2}&{{{\mathit{\boldsymbol{\delta }}}}_{{\mathit{\boldsymbol{s}}}}^2} \\ {{{\mathit{\boldsymbol{\delta }}}}_{{\mathit{\boldsymbol{s}}}}^2}&{{{\mathit{\boldsymbol{\delta }}}}_{{\mathit{\boldsymbol{s}}}}^2}&{2{{\mathit{\boldsymbol{\delta }}}}_{{\mathit{\boldsymbol{s}}}}^2} \end{array}} \right]$

式中： ${{\mathit{\boldsymbol{\delta }}}}_{\Delta {{\mathit{\boldsymbol{r}}}}}^2$ 为时差测量误差的标准差，各站之间时差测量值不相关； ${{\mathit{\boldsymbol{\delta }}}}_{{\mathit{\boldsymbol{s}}}}^2$ 为各站位置绝对误差，各站绝对位置误差在各个分量上的方差相同，并且位置误差与时差测量误差之间互不相关。将 ${{{\mathit{\boldsymbol{R}}}}_k}$ 代入标准卡尔曼滤波递推方程中进行滤波处理，得到辐射源位置估计值 ${{\hat{{\mathit{\boldsymbol{u}}}}}_k}$ 。

为了体现多次定位卡尔曼滤波结果，本节仿真参数如下：辐射源为地面固定目标，其位置坐标与上节相同；四站位置如表1所示，运动速度为 $( - 0.5, - 2, - 0.5)$ km/s，观测时长为10 s，观测间隔时间为0.1 s；仿真中时差测量误差为10 ns，各站绝对位置误差为5 m。

从图4中可以看出，对多次定位结果进行卡尔曼滤波后，辐射源定位误差大大减小，到4 s以后，定位误差稳定在10 m以下，滤波处理可以大大提升对辐射源的定位精度。

4 结论

本文以四站时差定位系统为例，考虑观测站位置误差对定位算法精度的影响，提出了一种基于凸优化的时差定位算法。通过将非线性的时差定位方程转换为一个凸优化问题，结合地球表面约束条件得到辐射源位置的最优解。仿真结果表明：本文算法在相同时差测量误差或位置误差条件下定位精度优于传统时差定位算法，在高误差条件下定位误差最小；进一步通过对多次定位结果进行卡尔曼滤波处理减小了辐射源定位误差，大大提升了辐射源定位精度。