平面连杆机构是多数机器的主机构，其基本机构为平面四杆(体)机构。凸轮机构和齿轮机构可以视为将1个构件(体)和2个转动副或移动副(二约束副)用1个高副(一约束副)替代的四体机构。采用串连、并连、封闭和装载等方式^[1-3]，平面四体机构可组合出各种复杂机构。平面四体机构的动力学研究属于机械原理的研究范畴。

当曲柄作为从动件时，存在曲柄压力角(受力方向与运动方向之间的夹角)为90°的位置。该位置称为歧运动位^[4](卡位、死点^[5-6])。根据从动件与连杆共线的特征，歧运动位存在于曲柄摇杆机构^[7]、双摇杆机构、双曲柄机构和曲柄滑块机构当中。运动如果可正可逆，也可称为运动分岔，但是与非线性动力学的仿真收敛性和响应分岔无关。

歧运动位是多年来的研究冷点，在平面四体机构当中普遍存在，但一直没有受到重视。在歧运动位，从动件存在双向运动可能性^[8-9]。

曲柄摇杆机构的曲柄从动件和摇杆从动件的运动学程序化计算机仿真^[10-12]涉及歧运动位，基于洛必达法则求取了歧运动位的从动件运动学参数计算式。但是，对于特殊的、多歧运动位的滑块机构尚无研究。由于该计算式尚未公开发表，ADAMS等计算软件是避开了歧运动位的计算，因此不做对比。

通常，对于连杆为最长杆的滑块机构，当曲柄或摇杆作为主动件时，从动件的位置、速度、加速度与主动件的存在一一对应关系，机构没有歧运动位^[13]。但是，当滑块为主动件，或连杆不是最长杆时，存在歧运动位。本文研究具有3个歧运动位的滑块机构动力学问题。

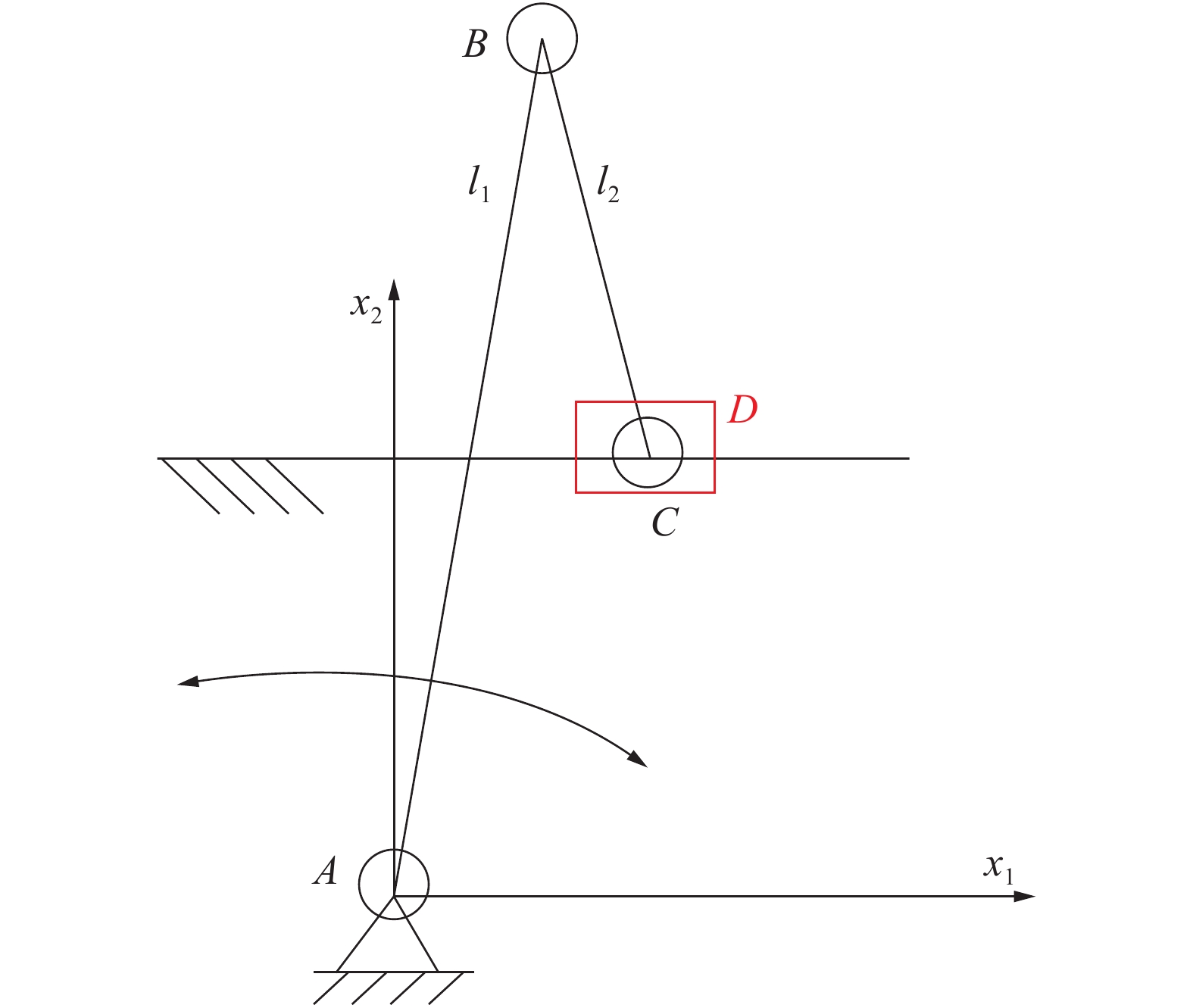
1 具有3个歧运动位的滑块机构

摇杆滑块机构如图1所示。

滑块的导路为经过另一运动副而与运动轨迹平行的直线或曲线。该导路距A点的距离为摇杆长度的一半。摇杆可在平角内摆动。机架(固定体)可视为由A指向滑块导路垂线无穷远端的无限长杆；滑块可延伸为由转动副C垂直于导路指向无穷远的无限长杆。以A为坐标原点，建立图1的直角坐标系 $ {x}_{1}A{x}_{2} $ 。 ${{{l}}_1}$ 、 ${{{l}}_2}$ 分别为摇杆AB和连杆BC的矢径，长度分别为 ${l_1}$ 、 ${l_2}$ 。 ${\theta _1}$ 、 ${\theta _2}$ 分别为 ${{{l}}_1}$ 、 ${{{l}}_2}$ 相对于 ${x_1}$ 轴正方向的夹角。d为A到滑块导路的垂直距离。d和 ${l_2}$ 均为 ${l_1}$ 的一半。C点相对于坐标原点的矢径为 ${{{l}}_3}$ 。根据各构件之间的几何关系，以及矢量方程的几何意义(等号两边的矢量分别首尾相接，形成2个矢量链，如果其起点相同，则终点重合)，可得矢量方程

${{{l}}_1} + {{{l}}_2} = {{{l}}_3}{\text{}}$

(1)

将式(1)分别向2个坐标轴投影，可得投影方程组

$\left\{ {\begin{array}{*{20}{l}} {{l_1}\cos {\theta _1} + {l_2}\cos {\theta _2} = {x_{{\rm{1}},C}}} \\ \begin{array}{l} {l_1}\sin {\theta _1} + {l_2}\sin {\theta _2} = d \\ {\theta _1} \in [ {\begin{array}{*{20}{c}} 0,{\rm{{\text{π}} }} \end{array}} ] \end{array} \end{array}} \right.{\text{}}$

(2)

式中 ${\theta _2}$ 和 ${x_{{\rm{1}},C}}$ 为未知量。

设摇杆按照正弦规律摆动，T为周期，根据式(2)， ${\theta _1}$ 及其各阶导数为

$\left\{ \begin{array}{l} {\theta _1} = \dfrac{{{\rm{{\text{π}} }} - 0}}{2}\sin \left( {\dfrac{{2{\rm{{\text{π}} }}}}{T}t} \right) + \dfrac{{{\rm{{\text{π}} }} + 0}}{2} \\ {{\dot \theta }_1} = \dfrac{{{{\rm{{\text{π}} }}^2}}}{T}\cos\left( {\dfrac{{2{\rm{{\text{π}} }}}}{T}t} \right) \\ {{\ddot \theta }_1} = - \dfrac{{2{{\rm{{\text{π}} }}^3}}}{{{T^2}}}\sin \left( {\dfrac{{2{\rm{{\text{π}} }}}}{T}t} \right) \\ {{\dddot \theta }_1} = - \dfrac{{4{{\rm{{\text{π}} }}^4}}}{{{T^3}}}\cos \left( {\dfrac{{2{\rm{{\text{π}} }}}}{T}t} \right) \\ {{\ddddot \theta }_1} = \dfrac{{8{{\rm{{\text{π}} }}^5}}}{{{T^4}}}\sin \left( {\dfrac{{2{\rm{{\text{π}} }}}}{T}t} \right) \end{array} \right.{\text{}}$

(3)

式(2)对时间依次求导，并整理成矩阵形式，可根据二阶矩阵求逆运算的简化公式求解出上述2个未知量的各阶导数。

在歧运动位， ${\theta _2}$ 对时间的各阶导数均为0/0型的不定式，可根据洛必达法则求解^[14]。

2 连杆位置角的讨论

对于图1的机构， ${\theta _1}$ 等于0、 ${\rm{{\text{π}} }}/2$ 、 ${\rm{{\text{π}} }}$ 的3个位置为机构的歧运动位。在 ${\theta _1}$ 等于 $ {\rm{{\text{π}} }}/2$ 的位置，由于连杆被摇杆拉动而没有卡位的特征，属于一般的歧运动位。而在另外2个位置，由于连杆被摇杆压住，如果滑块保持静止并且受到的水平力 ${F_{{\rm{1,}}D}}$ =0，则无论摇杆的驱动力多么大，机构均保持静止，因此，这2个位置位置均为机构的卡位。

根据式(2)， ${\theta _2}$ 有以下2个计算式：

${\theta _2} = \arcsin \left( {\frac{{d - {l_1}\sin {\theta _1}}}{{{l_2}}}} \right){\text{}}$

(4)

${\theta _2} = {\rm{{\text{π}} }} - \arcsin \left( {\frac{{d - {l_1}\sin {\theta _1}}}{{{l_2}}}} \right){\text{}}$

(5)

考虑惯性力，计算滑块受力 ${F_{{\rm{1,}}D}}$ 和速度 ${\dot x_{{\rm{1}},C}}$ ，在接下来 ${\theta _1}$ 连续运动的 $\dfrac{{\rm{{\text{π}} }}}{2}$ 范围内， ${\theta _2}$ 取式(4)计算的情况有

$\left\{ {\begin{array}{*{20}{l}} {{{\dot x}_{{\rm{1}},C}} > 0} \\ {{{\dot x}_{{\rm{1}},C}} = = 0\& \& {F_{{\rm{1,}}D}} > 0} \end{array}} \right.{\text{}}$

(6)

${\theta _2}$ 取式(5)计算的情况有

$\left\{ {\begin{array}{*{20}{l}} {{{\dot x}_{{\rm{1}},C}} < 0} \\ {{{\dot x}_{{\rm{1}},C}} = = 0\& \& {F_{{\rm{1,}}D}} < 0} \end{array}} \right.{\text{}}$

(7)

机构保持静止的2个条件为

$\left\{ {\begin{array}{*{20}{l}} {{{\dot x}_{{\rm{1}},C}} = = 0} \\ {{F_{{\rm{1,}}D}} = = 0} \end{array}} \right.{\text{}}$

(8)

在 ${\theta _1} = {\rm{{\text{π}} }}/2$ 的位置，在接下来 ${\theta _1}$ 连续运动的 $\dfrac{{\rm{{\text{π}} }}}{2}$ 范围内， ${\theta _2}$ 取式(4)计算的情况有

$\left\{ {\begin{array}{*{20}{l}} {{{\dot \theta }_2} > 0} \\ {{{\dot \theta }_2} = = 0\& \& {F_{{\rm{1,}}D}} > 0} \end{array}} \right.{\text{}}$

(9)

${\theta _2}$ 取式(5)计算的情况有

$\left\{ {\begin{array}{*{20}{l}} {{{\dot \theta }_2} < 0} \\ {{{\dot \theta }_2} = = 0\& \& {F_{{\rm{1,}}D}} < 0} \end{array}} \right.{\text{}}$

(10)

如果机构满足以下条件：

$\left\{ {\begin{array}{*{20}{l}} {{{\dot \theta }_2} = = 0} \\ {{F_{{\rm{1,}}D}} = = 0} \end{array}} \right.$

(11)

则机构保持静止。

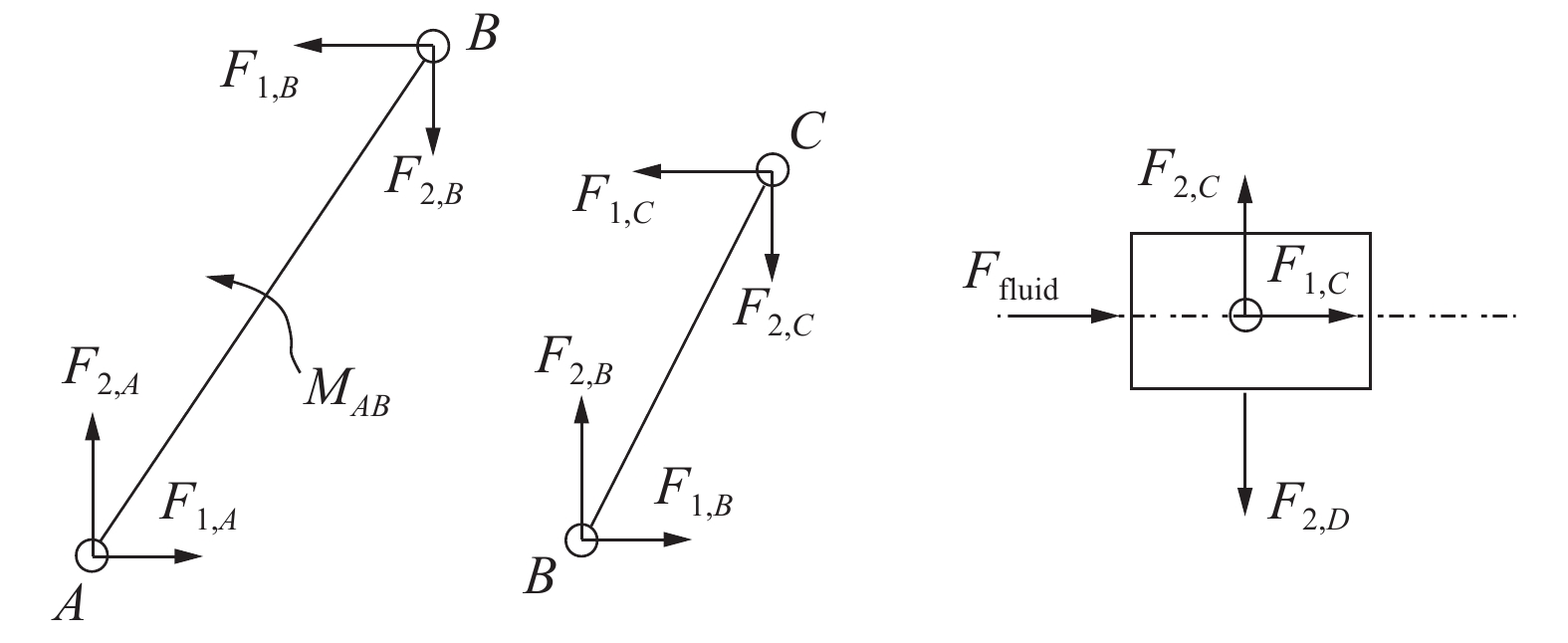
3 各构件的受力分析

分别取摇杆、连杆和滑块为研究对象，进行受力分析。如图2所示，在每个体的输入端令所受力的正方向与坐标轴方向相同，在输出端相反，则每个运动副处的作用力和反作用力可用相同的变量表示^[15]。在图2中没有标出惯性力和重力等。

设摇杆在驱动力矩 ${M_{AB}}$ 的作用下按照式(3)的规律摆动。忽略各运动副之间的摩擦力^[16]。设滑块在导路中受到阻尼系数为c的流体作用^[17]，流体流速为 ${v_{{\rm{fluid}}}}$ ，方向与 ${x_{\rm{1}}}$ 轴正方向相同。根据图2的受力分析，机构的未知量为 ${M_{AB}}$ 、 ${F_{{\rm{1,}}A}}$ 、 ${F_{{\rm{2,}}A}}$ 、 ${F_{{\rm{1,}}B}}$ 、 ${F_{{\rm{2,}}B}}$ 、 ${F_{{\rm{1,}}C}}$ 、 ${F_{{\rm{2,}}C}}$ 、 ${F_{{\rm{2,}}D}}$ ，共8个，根据作平面运动物体的动力学方程^[18-19]，由3个体可分别列出3、3、2个方程，可得8个方程的方程组。方程数与未知量数相同，可解。该建模方法比拉格朗日方法^[20]更直观。如果考虑原动机的机械特性^[20-21]，则 ${M_{AB}}$ 是 ${\dot \theta _{\rm{1}}}$ 的函数，该未知量换为 ${\ddot \theta _{\rm{1}}}$ 。

设3个体的质量分别为 ${m_{\rm{1}}}$ 、 ${m_{\rm{2}}}$ 、 ${m_{\rm{3}}}$ 。设质心均在其几何中心上，且质量分布均匀，则摇杆和连杆绕质心的转动惯量分别为

$\left\{ {\begin{array}{*{20}{l}} {{J_1} = \dfrac{1}{{12}}{m_1}l_1^2} \\ {{J_2} = \dfrac{1}{{12}}{m_2}l_2^2} \end{array}} \right.{\text{}}$

(12)

设摇杆和连杆的输入端到质心的距离分别为 ${l_{{\rm{1a}}}}$ 、 ${l_{{\rm{2a}}}}$ ，则由摇杆可列出3个动力学方程：

$ - {m_1}{l_{1{\rm{a}}}}\left( { - {{\ddot \theta }_1}\sin {\theta _1} - \dot \theta _1^2\cos{\theta _1}} \right) + {F_{1,A}} - {F_{1,B}} = 0{\text{}}$

(13)

$ - {m_1}{l_{1{\rm{a}}}}\left( {{{\ddot \theta }_1}\cos{\theta _1} - \dot \theta _1^2\sin{\theta _1}} \right) + {F_{2,A}} - {F_{2,B}} - {m_1}g = 0{\text{}}$

(14)

$\begin{split}& - \frac{{{m_1}l_1^2}}{{12}}{{\ddot \theta }_1} + {M_{AB}} + {F_{1,A}}{l_{1{\rm{a}}}}\sin{\theta _1} - {F_{2,A}}{l_{1{\rm{a}}}}\cos{\theta _1}+ \\& \;\;\; {F_{1,B}}\left( {{l_1} - {l_{1{\rm{a}}}}} \right)\sin{\theta _1} - {F_{2,B}}\left( {{l_1} - {l_{1{\rm{a}}}}} \right)\cos{\theta _1} = 0 \end{split} {\text{}}$

(15)

由连杆可列出3个动力学方程：

$\begin{split}&\quad\quad\; - {m_2}{l_1}\left( { - {{\ddot \theta }_1}\sin {\theta _1} - \dot \theta _1^2\cos{\theta _1}} \right) -\\& {m_2}{l_{2{\rm{a}}}}\left( { - {{\ddot \theta }_2}\sin {\theta _2} - \dot \theta _2^2\cos{\theta _2}} \right) + {F_{1,B}} - {F_{1,C}} = 0 {\text{}}\end{split}$

(16)

$\begin{split}& \quad - {m_2}{l_1}\left( {{{\ddot \theta }_1}\cos{\theta _1} - \dot \theta _1^2\sin{\theta _1}} \right) - {m_2}g- \\& {m_2}{l_{2{\rm{a}}}}\left( {{{\ddot \theta }_2}\cos{\theta _2} - \dot \theta _2^2\sin{\theta _2}} \right) + {F_{2,B}} - {F_{2,C}} = 0 {\text{}}\end{split}$

(17)

$\begin{split}& \;\; - \frac{{{m_2}l_2^2}}{{12}}{{\ddot \theta }_2} + {F_{1,B}}{l_{2{\rm{a}}}}\sin{\theta _2} - {F_{2,B}}{l_{2{\rm{a}}}}\cos{\theta _2} +\\ & {F_{1,C}}\left( {{l_2} - {l_{2{\rm{a}}}}} \right)\sin{\theta _2} - {F_{2,C}}\left( {{l_2} - {l_{2{\rm{a}}}}} \right)\cos{\theta _2} = 0 {\text{}}\end{split}$

(18)

由滑块可列出2个动力学方程

$ - {m_3}{\ddot x_{{\rm{1}},C}} + c\left( {{v_{{\rm{fluid}}}} - {{\dot x}_{{\rm{1}},C}}} \right) + {F_{{\rm{1}},C}} = 0{\text{}}$

(19)

${F_{2,C}} - {F_{2,D}} - {m_3}g = 0{\text{}}$

(20)

式(13)—式(20)组成的方程组写成矩阵形式，则具有稀疏系数矩阵。如果采用计算量较大的方程组求解方法，则在歧运动位会由于其系数矩阵奇异而不能求出较准确的未知量。分析各方程，可依照以下顺序求解。

1)由式(19)求 ${F_{{\rm{1}},C}}$ 。

${F_{1{\rm{C}}}} = {m_3}{\ddot x_{{\rm{1}},C}} - c\left( {{v_{{\rm{fluid}}}} - {{\dot x}_{{\rm{1}},C}}} \right){\text{}}$

(21)

2)由式(16)求 ${F_{1,B}}$ 。

$\begin{split}& {F_{1,B}} = {F_{1,C}} + {m_2}{l_1}\left( { - {{\ddot \theta }_1}\sin {\theta _1} - \dot \theta _1^2\cos{\theta _1}} \right)+ \\& \quad \quad {m_2}{l_{2{\rm{a}}}}\left( { - {{\ddot \theta }_2}\sin {\theta _2} - \dot \theta _2^2\cos{\theta _2}} \right) {\text{}}\end{split}$

(22)

3)由式(13)求 ${F_{1,A}}$ 。

${F_{1,A}} = {F_{1,B}} + {m_1}{l_{1{\rm{a}}}}\left( { - {{\ddot \theta }_1}\sin {\theta _1} - \dot \theta _1^2\cos{\theta _1}} \right){\text{}}$

(23)

4)由式(17)和式(18)求 ${F_{2,B}}$ 和 ${F_{2,C}}$ 。

${F_{2,B}} = \dfrac{{{B_4} - {B_2}}}{{1 + \dfrac{{{l_{2{\rm{a}}}}}}{{{l_2} - {l_{2{\rm{a}}}}}}}}{\text{}}$

(24)

${F_{2,C}} = - {F_{2,B}} - {B_2} = {F_{2,B}} - {B_4}{\text{}}$

(25)

式中：

$\begin{split}& {B_4} = {m_2}{l_1}\left( {{{\ddot \theta }_1}\cos{\theta _1} - \dot \theta _1^2\sin{\theta _1}} \right) + {m_2}g +\\& \quad \quad {m_2}{l_{2{\rm{a}}}}\left( {{{\ddot \theta }_2}\cos{\theta _2} - \dot \theta _2^2\sin{\theta _2}} \right) {\text{}}\end{split}$

(26)

${B_2} = \dfrac{{\dfrac{{{m_2}l_2^2}}{{12}}{{\ddot \theta }_2} - \left( {{l_{2{\rm{a}}}}{F_{1,B}} + \left( {{l_2} - {l_{2{\rm{a}}}}} \right){F_{1,C}}} \right)\sin{\theta _2}}}{{\left( {{l_2} - {l_{2{\rm{a}}}}} \right)\cos{\theta _2}}}{\text{}}$

(27)

在歧运动位，由力矩平衡方程而得的 ${B_2}$ 为0/0型不定式，可由洛必达法则简化为

$\begin{split}{B_2} = &\frac{ \dfrac{{{m_2}l_2^2}}{{12}}{{\dddot \theta }_2} - \left( {{l_{2{\rm{a}}}}{{\dot F}_{1,B}} + \left( {{l_2} - {l_{2{\rm{a}}}}} \right){{\dot F}_{1,C}}} \right)\sin {\theta _2}}{{{- \left( {{l_2} - {l_{2{\rm{a}}}}} \right){{\dot \theta }_2}\sin {\theta _2}}}}+\\ & \frac{{ - {F_{1,B}}{l_{2{\rm{a}}}}\cos {\theta _2}{{\dot \theta }_2} - {F_{1,C}}\left( {{l_2} - {l_{2{\rm{a}}}}} \right)\cos {\theta _2}{{\dot \theta }_2}}}{{ - \left( {{l_2} - {l_{2{\rm{a}}}}} \right){{\dot \theta }_2}\sin {\theta _2}}} = \\ & - \frac{{{m_2}l_2^2{{\dot \theta }_2}}}{{12\left( {{l_2} - {l_{2{\rm{a}}}}} \right){{\dddot \theta }_2}\sin {\theta _2}}} + \frac{{{l_{2{\rm{a}}}}{{\dot F}_{1,B}} + \left( {{l_2} - {l_{2{\rm{a}}}}} \right){{\dot F}_{1,C}}}}{{\left( {{l_2} - {l_{2{\rm{a}}}}} \right){{\dot \theta }_2}}} {\text{}}\end{split}$

(28)

由式(21)和式(22)，可得式(28)中的力导数。

$\begin{split}& {l_{2{\rm{a}}}}{{\dot F}_{1,B}} + \left( {{l_2} - {l_{2{\rm{a}}}}} \right){{\dot F}_{{\rm{1}},C}} = {l_2}{m_3}{{\dddot x}_{{\rm{1}},C}} + {l_2}c{{\ddot x}_{{\rm{1}},C}}-\\& \quad {m_2}{l_1}{l_{2{\rm{a}}}}\left( {{{\dddot \theta }_1}\sin {\theta _1} + 3{{\dot \theta }_1}{{\ddot \theta }_1}\cos{\theta _1} - \dot \theta _1^3\sin {\theta _1}} \right) -\\& \quad {m_2}{l_{2{\rm{a}}}}{l_{2{\rm{a}}}}\left( {{{\dddot \theta }_2}\sin {\theta _2} + 3{{\dot \theta }_2}{{\ddot \theta }_2}\cos{\theta _2} - \dot \theta _2^3\sin {\theta _2}} \right) {\text{}}\end{split}$

(29)

5)由式(20)求 ${F_{{\rm{2,}}D}}$ 。

${F_{2,D}} = {F_{2,C}} - {m_3}g{\text{}}$

(30)

6)由式(14)求 ${F_{{\rm{2,}}A}}$ 。

${F_{2,A}} = {m_1}{l_{1{\rm{a}}}}\left( {{{\ddot \theta }_1}\cos{\theta _1} - \dot \theta _1^2\sin{\theta _1}} \right) + {F_{2,B}} + {m_1}g{\text{}}$

(31)

7)由式(15)求 ${M_{AB}}$ 。

$\begin{split}& {M_{AB}} = \frac{{{m_1}l_1^2}}{{12}}{{\ddot \theta }_1} - \left( {{l_{1{\rm{a}}}}{F_{1,A}} + \left( {{l_1} - {l_{1{\rm{a}}}}} \right){F_{1,B}}} \right)\sin{\theta _1} +\\& \quad \quad \quad \left( {{l_{1{\rm{a}}}}{F_{2,A}} + \left( {{l_1} - {l_{1{\rm{a}}}}} \right){F_{2,B}}} \right)\cos{\theta _1} {\text{}}\end{split}$

(32)

4 计算机仿真结果 4.1 机构的基本参数

主动摇杆的主要参数为： $ {m}_{1}=5.0\;{\rm{kg}} $ ； $ {l}_{1}= $ $ 1.0\;{\rm{m}} $ ； $ {l}_{1{\rm{a}}}=0.5\;{\rm{m}} $ ； ${J}_{1}=\dfrac{5}{12}\;{\rm{kg}}\cdot {\;{\rm{m}}}^{2}$ 。

连杆的主要参数为： $ {m}_{2}=2.5\;{\rm{kg}} $ ； $ {l}_{2}= $ $ 0.5\;{\rm{m}} $ ； $ {l}_{2{\rm{a}}}=0.25\;{\rm{m}} $ 、 ${J}_{2}=\dfrac{5}{96}\;{\rm{kg}}\cdot {\;{\rm{m}}}^{2}$ 。

滑块的主要参数为： $ {m}_{3}=5\;{\rm{kg}} $ ；d=0.5 m。

滑块所在导路的流体速度 $ {v}_{\rm{fluid}}=1.0\;{\rm{m/s}} $ ，流体的阻尼系数c=0.1N/(m/s)。

摇杆的摆动周期 $ T{\rm{ = 9}}{\rm{.0}}\;{\rm{s}}$ ，计算机仿真步长 $ \delta {\rm{ = 0}}{\rm{.01}}\;{\rm{s}}$ 。

4.2 程序化仿真结果

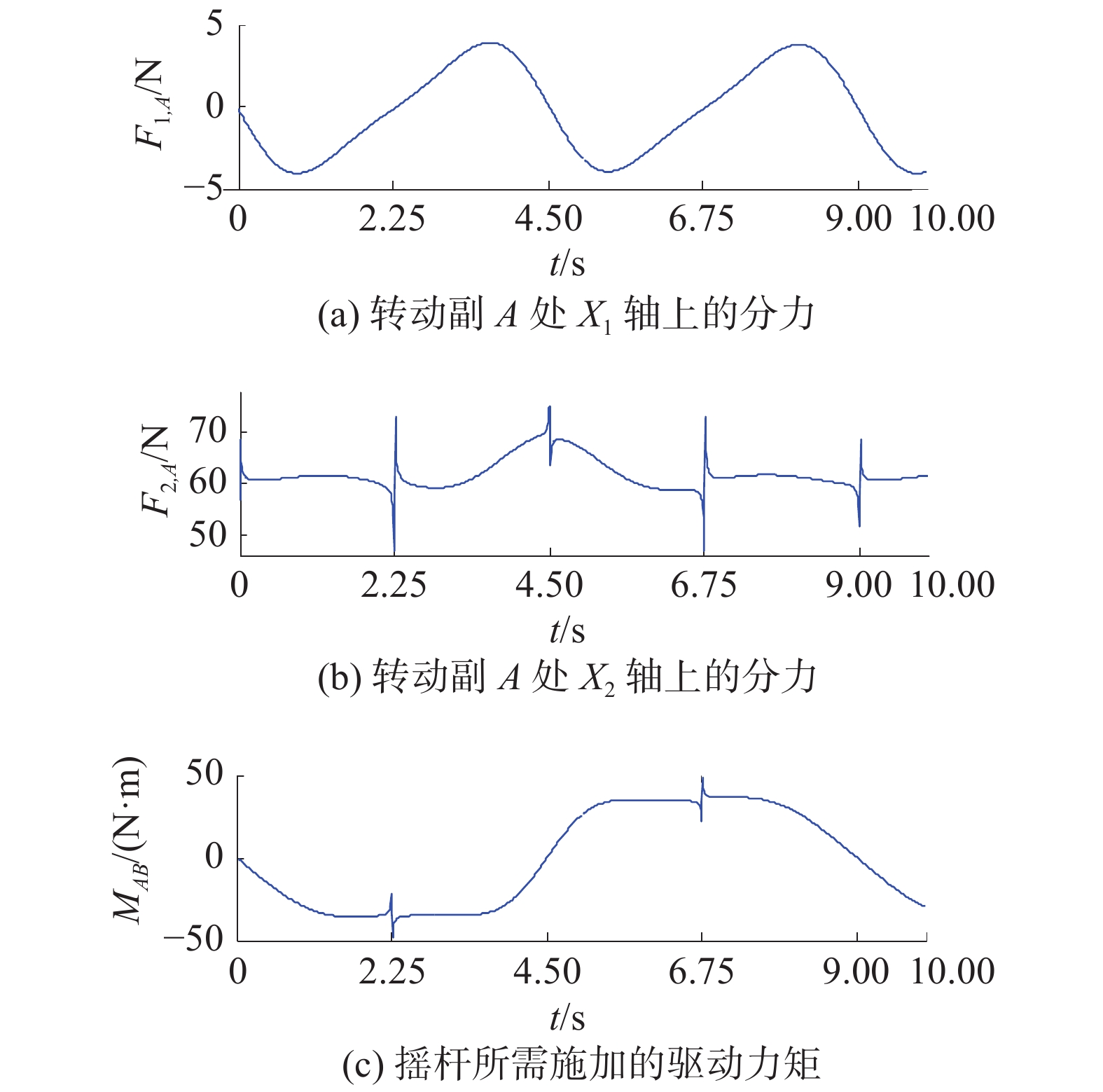
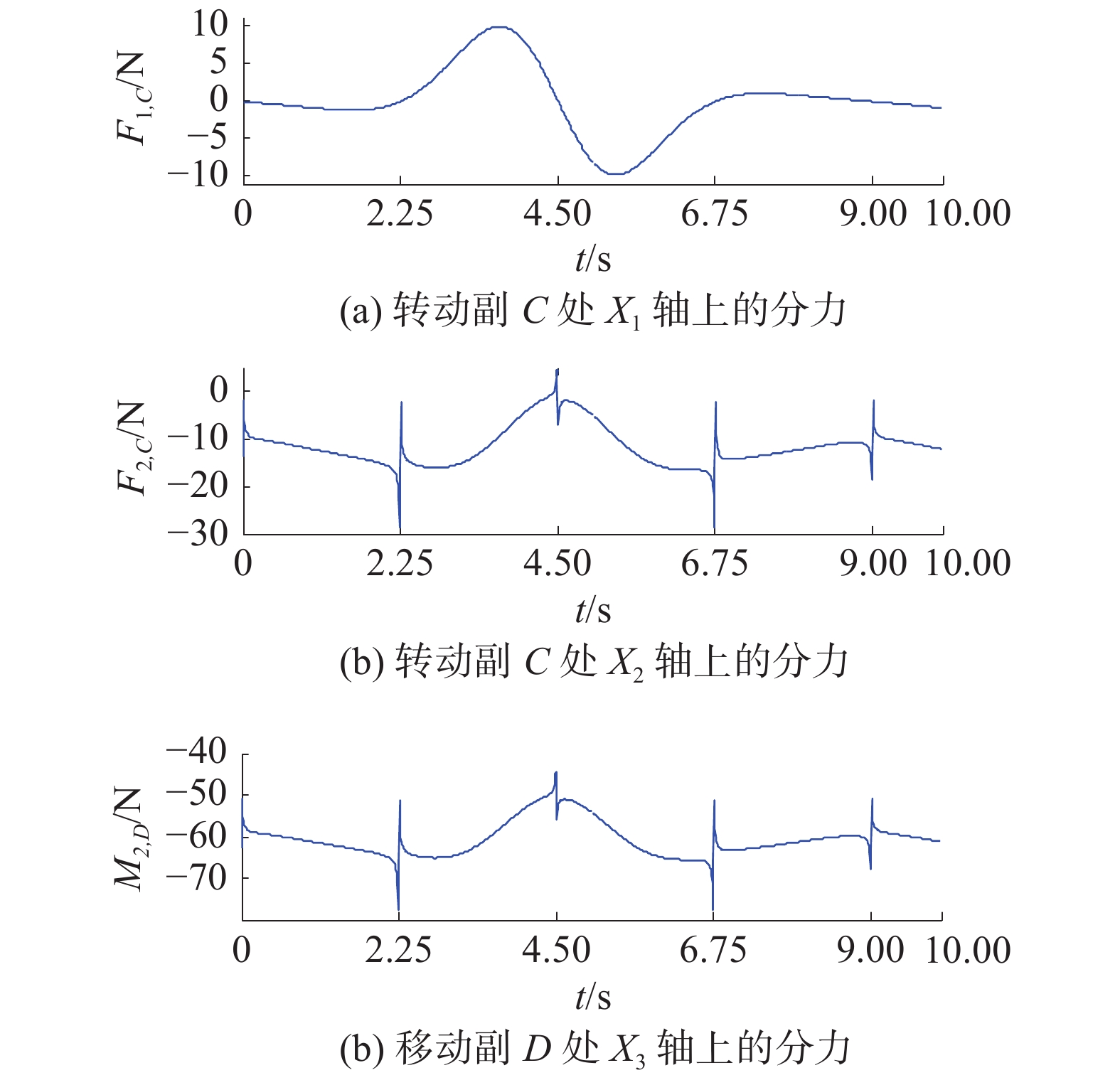
摇杆的输入端受力如图3所示，滑块的受力如图4所示，连杆的输入端受力如图5所示。力存在突然变化的情况，说明存在柔性冲击。

5 结论

1)本文研究的平面四体机构具有3个歧运动位，其中2个是卡位。该机构具有一定的代表性。

2)当主动摇杆按照正弦规律摆动时，机构平稳运动，不出现速度突变和加速度突变，但是，垂直方向受力出现大趋势突变，存在柔性冲击。因此，该机构宜用于仪器仪表等微小功率的应用领域。

3)本文不涉及实践研究，不分析该机构及其相近机构的实践意义和可适用的工作场合。

4)位移表征物体的位置、姿态、运动轨迹，坐标的三阶及更高阶导数不能用于类似于牛顿第二定律的计算式，但是其理论意义仍不可忽视。

5)基于洛必达法则研究的歧运动位运动学参数和力使动力学仿真顺利进行。

6)提出的力导数概念具有较大的理论意义。