5G作为新一代信息通讯发展的主要方向,将渗透到未来社会的各个领域,它以为用户提供更高的数据速率和为众多的物联网设备提供多条连接为目标。相比于4G,5G通信的频谱效率提升5~15倍,能效和成本效率提升百倍[1]。大规模多输入多输出(multiple input multiple output,MIMO)技术和毫米波通信技术作为5G的关键技术,发挥着重要的作用。大规模MIMO技术是在通信系统的收发两端均采用多个天线单元对传输信号进行发送和接收,通过空间复用、波束赋型、预编码等技术,充分利用无线信道的空间资源,提高系统稳定性,降低系统的误码率,简化信号处理方式,减少系统时延。目前6、15、18、28、45、60 GHz和72 GHz都是业界开展5G研究的典型候选频段。而6~100 GHz频率范围是典型的毫米波频段,在该范围内的通信可为热点用户提供更高的容量,可支持10 GB/s以上的用户传输速率[2-3]。毫米波主要以直射波的形式在空间中传播,波束窄,具有良好的方向性,但是受环境的影响大,如降雨、沙尘等,传播距离有限[4-5]。由于毫米波属于甚高频,所以波长小,能够在有限的物理空间中封装大量天线,利用阵列天线和预编码技术结合,能够有效弥补毫米波的传输损耗,增大传输距离,提高系统的稳定性[6]。
在大规模MIMO系统中使用预编码技术能够提高系统的频谱效率,降低误码率,简化接收机的复杂度。在4G通信系统中,传统的数字预编码技术已经得到了广泛的应用。为了实现大规模MIMO技术的最大理论优势[7],传统数字预编码技术需要为每根发射天线配备独立的射频链路。但是在毫米波大规模MIMO系统中,由于发射天线的数量巨大,如果依然采用传统的数字预编码技术将会导致系统硬件成本过高,系统功耗过大。因此,在毫米波大规模MIMO系统,一般采用混合预编码技术,即将预编码处理分为基带预编码(数字预编码)处理和射频预编码(模拟预编码)处理[8]。该方案只使用了少量的射频链路,从而解决传统数字预编码的高成本和高功耗的问题。
混合预编码是将多路发送信号经过基带预编码器处理后,通过射频链路发送到射频预编码器进行恒模移相,然后发送到发射天线发射出去。毫米波大规模MIMO系统的混合预编码架构可分为共享阵列型架构和分离子阵列型架构[9],其中共享阵列型架构的每个射频链路和所有的发射天线相连,而分离子阵列架构的每个射频链路只与部分发射天线相连。共享阵列型架构相对于分离子阵列型架构硬件设计复杂、功耗高,但是其能充分发挥预编码性能,达到比较好的效果。因此,本文的研究基于共享阵列型架构。
在毫米波大规模MIMO系统的混合预编码研究中,文献[10]利用发射器和接收器在多分辨率码本下共同设计模拟波束形成向量。文献[11]引入了波束空间多输入多输出,利用离散傅里叶变换(discrete fourier transform,DFT)波束形成向量将发射信号引导到具有接收信号功率渐进最大化的子空间。文献[9]根据毫米波信道的稀疏性,将混合预编码问题转换为稀疏重构问题。在假设完美已知信道信息的条件下,利用正交匹配追踪的概念,提出了低复杂度的混合预编码算法。但是文献[12]的射频预编码的设计是需要在每次迭代过程中从候选矩阵选出与残差的内积相乘最大的一列,而其中的候选矩阵的构造需要高精度的信道估计来完成,即需要估计信号发射角和到达角,这将会造成系统延时,并且消耗系统资源。同时该算法在更新基带预编码时采用最小二乘法进行矩阵求逆,矩阵求逆的复杂度随着基向量的数量增加而增加,高维度的矩阵求逆将会导致较长的计算延时和较高的功率消耗。在文献[13]中,针对单数据流的单用户MIMO-OFDM系统,提出了一种混合预编码以使接收信号强度最大化。
因此,本文针对文献[12]存在的问题,利用BSA解决需要已知候选矩阵的问题,直接搜索与残差的内积相乘最大的阵列响应矢量,同时利用Banachiewicz-Schur分块矩阵广义逆[14],将高维度的矩阵转换为低维度的矩阵,并利用每次迭代的结果,避免矩阵求逆,简化系统的计算量。仿真结果表明,所提出的算法在在无需已知候选矩阵和矩阵求逆的条件下,系统的频谱效率和误码率相比基于OMP的混合预编码性能略有提升。
1 系统模型毫米波大规模MIMO系统的共享型阵列架构如图 1所示。其中,发射端的发射天线数为Nt,接收端的接收天线数为Nr,发射端的射频链路数为NtRF,接收端的射频链路数为NrRF,发送端和接收端的数据流都为Ns。
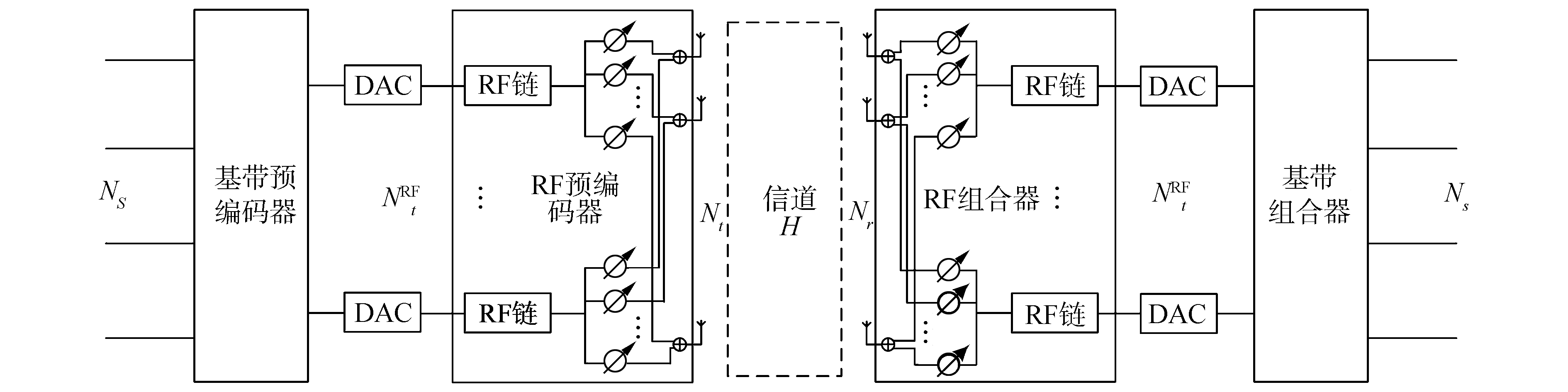
|
Download:
|
| 图 1 频域脉冲压缩方法框图 | |
为了保证多数据流传输,需要满足Ns≤NtRF≤Nt和Ns≤NrRF≤Nr。在这种硬件结构下,信号通过基带预编码器FBB∈
| $ x = {\mathit{\boldsymbol{F}}_{{\rm{RF}}}}{\mathit{\boldsymbol{F}}_{{\rm{BB}}}}\mathit{\boldsymbol{s}} $ |
式中:s=[s1,s2,...,sNs]T为信号的数据流,且
经过信道传输到达接收端天线的接收信号为
| $ y = \sqrt \rho \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{F}}_{{\rm{RF}}}}{\mathit{\boldsymbol{F}}_{{\rm{BB}}}}s + n $ |
式中:n∈
对接收信号利用射频组合器WRF∈
| $ \hat y = \sqrt \rho \mathit{\boldsymbol{W}}_{{\rm{BB}}}^{\rm{H}}\mathit{\boldsymbol{W}}_{{\rm{RF}}}^{\rm{H}}\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{F}}_{{\rm{RF}}}}{\mathit{\boldsymbol{F}}_{{\rm{BB}}}}\mathit{\boldsymbol{s}} + \mathit{\boldsymbol{W}}_{{\rm{BB}}}^{\rm{H}}\mathit{\boldsymbol{W}}_{{\rm{RF}}}^{\rm{H}}n $ |
式中
考虑到毫米波信道的高路径损耗和在空间上稀疏分布的特点,以及在大规模MIMO系统中收发机上天线阵列排列紧密,天线单元相关度高等的影响,传统的衰落统计信道模型并不适用,因此通常采用射线追踪模型进行建模。若毫米波信道中包含Ncl个散射簇,每簇包含Nray条传播路径,则系统的信道H可以描述为
| $ \mathit{\boldsymbol{H}} = \sqrt {\frac{{{N_t}{N_r}}}{{{N_{{\rm{cl}}}}{N_{{\rm{ray}}}}}}} \sum\limits_{i,l} {{\alpha _{i,l}}{a_r}\left( {\varphi _{il}^r} \right){a_t}{{\left( {\varphi _{il}^t} \right)}^{\rm{H}}}} $ |
式中:αi,l表示第i个散射簇中的第l条传播路径的增益因子,服从均值为0、方差为σα,i2的复高斯分布,且满足
根据天线在阵列中排列的不同,天线阵列的类型可以组合成各种样式。在毫米波大规模MIMO系统中,一般会选择均匀天线阵列来对收发两端天线进行设计。常见的均匀天线阵列有均匀线性阵列和均匀平面阵列。为了分析方便,本文采用均匀线性阵列。对于均匀线性阵列,假设在一个y轴上拥有N个天线,则其阵列响应向量可以表示为
| $ \mathit{\boldsymbol{a}}\left( \varphi \right) = \sqrt {\frac{1}{N}} {\left[ {1,{{\rm{e}}^{jkd\sin \left( \varphi \right)}},{{\rm{e}}^{j2kd\sin \left( \varphi \right)}}, \cdots ,{{\rm{e}}^{j\left( {N - 1} \right)kd\sin \left( \varphi \right)}}} \right]^{\rm{T}}} $ |
式中:φ∈[0,2π],k=2π/λ,d为天线单元间距。在实际的系统中,信道状态信息(channel state information,CSI)可以通过信道估计得知。为了只关注于预编码的研究,假设收发端确知CSI,则系统的频谱效率为
| $ \begin{array}{*{20}{c}} {R = }\\ {{{\log }_2}\left| {{I_{{N_s}}} + \frac{\rho }{{{N_s}}}\mathit{\boldsymbol{R}}_n^{ - 1}\mathit{\boldsymbol{W}}_{{\rm{BB}}}^{\rm{H}}\mathit{\boldsymbol{W}}_{{\rm{RF}}}^{\rm{H}}\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{F}}_{{\rm{RF}}}}{\mathit{\boldsymbol{F}}_{{\rm{BB}}}}\mathit{\boldsymbol{F}}_{{\rm{BB}}}^{\rm{H}}\mathit{\boldsymbol{F}}_{{\rm{RF}}}^{\rm{H}}{\mathit{\boldsymbol{H}}^{\rm{H}}}{\mathit{\boldsymbol{W}}_{{\rm{RF}}}}{\mathit{\boldsymbol{W}}_{{\rm{BB}}}}} \right|} \end{array} $ |
式中
| $ \begin{array}{*{20}{c}} {\left( {\mathit{\boldsymbol{F}}_{{\rm{RF}}}^{{\rm{opt}}},\mathit{\boldsymbol{F}}_{{\rm{BB}}}^{{\rm{opt}}}} \right) = \mathop {\arg \min }\limits_{{\mathit{\boldsymbol{F}}_{{\rm{RF}}}},{\mathit{\boldsymbol{F}}_{{\rm{BB}}}}} {{\left\| {{\mathit{\boldsymbol{F}}_{{\rm{opt}}}} - {\mathit{\boldsymbol{F}}_{{\rm{RF}}}}{\mathit{\boldsymbol{F}}_{{\rm{BB}}}}} \right\|}_F}}\\ {{\rm{s}}.{\rm{t}}.\;\;\;\;{\mathit{\boldsymbol{F}}_{{\rm{RF}}}} \in {F_{{\rm{RF}}}},\left\| {{\mathit{\boldsymbol{F}}_{{\rm{RF}}}}{\mathit{\boldsymbol{F}}_{{\rm{BB}}}}} \right\|_F^2 = {N_s}} \end{array} $ |
式中Fopt是全数字预编码矩阵,其为信道矩阵H的右奇异矩阵的前Ns列。则这个预编码设计问题可以表示为在满足FRF∈FRF条件下,找到Fopt在混合预编码器FRFFBB集合构成的子空间上的投影。同理,接收端的组合器设计方法类似。
2 基于BSA的MIB-OMP混合预编码 2.1 基于BSA的解决办法由于基于OMP的混合预编码算法利用候选矩阵选出与残差的内积相乘最大的一列来构造射频预编码器,其中候选矩阵由天线阵列响应矢量构造。通过观察阵列响应矢量的结构,可以发现只要确定了AOA的角度就可以构造出完整的阵列响应矢量,所以在这里本文利用BSA算法搜索与残差的内积相乘最大的阵列响应矢量,即寻求以下目标函数的全局最优解:
| $ f\left( w \right) = \mathop {\arg \max }\limits_\mathit{\boldsymbol{W}} \left\{ {\mathit{\boldsymbol{\psi }}{\mathit{\boldsymbol{\psi }}^{\rm{H}}}} \right\} $ | (1) |
式中:ψ=wHFres为相关向量,Fres为残差矩阵,
BSA是从鸟群的社会行为和社会互动中提取的群体智能[15]。鸟类主要有3种行为:觅食行为、警惕行为和飞行行为。
每只鸟都根据自己的经验和群体的经验寻找食物。其可以表示为
| $ \begin{array}{*{20}{c}} {x_{i,j}^{t + 1} = x_{i,j}^t + \left( {{p_{i,j}} - x_{i,j}^t} \right) \times C \times {\rm{rand}}\left( {0,1} \right) + }\\ {\left( {{g_j} - x_{i,j}^t} \right) \times S \times {\rm{rand}}\left( {0,1} \right)} \end{array} $ |
式中:xi,jt表示第i只鸟迭代t次时的位置,鸟类总数为N,i∈[1,N],j为维度;rand(0,1)表示(0,1)中独立的均匀分布随机数;C和S为两个正数,分别叫认知加速因子和社会加速因子;pi,j表示第i只鸟的最佳位置;而gj表示鸟群出现过的最佳位置。
每只鸟都可以在警惕行为和觅食行为之间切换。如果一只鸟在(0,1)的随机数小于阈值P,P∈(0,1),这只鸟会寻找食物。否则,这只鸟将继续保持警惕。
鸟类会试图移动到鸟群的中心,它们将不可避免地相互竞争。因此,每只鸟不会直接向鸟群中心移动。这些移动可以表示为
| $ \begin{array}{*{20}{c}} {x_{i,j}^{t + 1} = x_{i,j}^t + {A_1}\left( {{\rm{mea}}{{\rm{n}}_j} - x_{i,j}^t} \right) \times {\rm{rand}}\left( {0,1} \right) + }\\ {{A_2}\left( {{p_{k,j}} - x_{i,j}^t} \right) \times S \times {\rm{rand}}\left( { - 1,1} \right)} \end{array} $ |
其中:
| $ {A_1} = {a_1} \times \exp \left( { - \frac{{p{\rm{Fi}}{{\rm{t}}_i}}}{{{\rm{sumFit}} + \varepsilon }} \times N} \right) $ |
| $ {A_2} = {a_2} \times \exp \left( {\left( {\frac{{p{\rm{Fi}}{{\rm{t}}_i} - p{\rm{Fi}}{{\rm{t}}_k}}}{{\left| {p{\rm{Fi}}{{\rm{t}}_k} - p{\rm{Fi}}{{\rm{t}}_i}} \right| + \varepsilon }}} \right)\frac{{N \times p{\rm{Fi}}{{\rm{t}}_k}}}{{{\rm{sumFit}} + \varepsilon }}} \right) $ |
式中:k(k≠i)是一个正整数,即随机选择一个介于1到N之间的整数;a1和a2是两个在[0,2]之间的正常数;pFiti表示第i只鸟最佳适应值;sumFit代表鸟群最佳适应值之和;ε为一小常数,用来避免除数为0;meanj表示鸟群第j维位置的平均值。
鸟类可能会飞到另一个地方以应对捕食威胁和觅食。当到达一个新的地点,它们会再次寻找食物。有些鸟扮演生产者的角色,会寻找食物补给,而另一些鸟则试图从生产者盗取食物。生产者和小偷的行为可描述为:
| $ x_{i,j}^{t + 1} = x_{i,j}^t + {\rm{rand}}n\left( {0,1} \right) \times x_{i,j}^t $ |
| $ x_{i,j}^{t + 1} = x_{i,j}^t + \left( {x_{i,j}^t - x_{i,j}^t} \right) \times FL \times {\rm{rand}}\left( {0,1} \right) $ |
式中:randn(0,1)表示一个服从标准正态分布的随机数;k∈{1,2,...,N},k≠i;FL∈[0,2]。
2.2 基于Banachiewicz-Schur分块矩阵广义逆的解决办法对于矩阵求逆,常利用Banachiewicz-Schur分块矩阵广义逆来替代,它将高维度矩阵转换为低维度矩阵,并利用前次迭代的结果进行更新,避免矩阵求逆,减少计算量。为方便起见,定义G为
| $ {\mathit{\boldsymbol{G}}_{I,J}} = \mathit{\boldsymbol{\varphi }}_I^{\rm{H}}{\mathit{\boldsymbol{\varphi }}_J} $ |
式中:φ是Nt×NclNray矩阵,其列由发送端的阵列响应矢量构成;I和J是两个任意的索引集;φI是由φ的索引集I列组成的子阵列。此外,设Ii为第i次迭代中所选基向量的索引集。因此,最小二乘解可以改写为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_{{\rm{BB}}}} = {{\left( {\mathit{\boldsymbol{F}}_{{\rm{RF}}}^{\rm{H}}} \right)}^{ - 1}}\mathit{\boldsymbol{F}}_{{\rm{RF}}}^{\rm{H}}{\mathit{\boldsymbol{F}}_{{\rm{opt}}}} = }\\ {{{\left( {\mathit{\boldsymbol{\varphi }}_{{I_i}}^{\rm{H}}{\mathit{\boldsymbol{\varphi }}_{{I_i}}}} \right)}^{ - 1}}\mathit{\boldsymbol{\varphi }}_{{I_i}}^{\rm{H}}{\mathit{\boldsymbol{F}}_{{\rm{opt}}}} = \mathit{\boldsymbol{G}}_{{I_i},{I_i}}^{ - 1}\mathit{\boldsymbol{\varphi }}_{{I_i}}^{\rm{H}}{\mathit{\boldsymbol{F}}_{{\rm{opt}}}}} \end{array} $ | (2) |
对式(2)中的矩阵GIi,Ii-1应用Banachiewicz-Schur分块矩阵广义逆,可将该矩阵改写为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{G}}_{{I_i},{I_i}}^{ - 1} = {{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{G}}_{{I_{i - 1}},{I_{i - 1}}}}}&{{\mathit{\boldsymbol{G}}_{{I_{i - 1}},k}}}\\ {{\mathit{\boldsymbol{G}}_{k,{I_{i - 1}}}}}&{{\mathit{\boldsymbol{G}}_{k,k}}} \end{array}} \right]}^{ - 1}} = }\\ {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{G}}_{{I_{i - 1}},{I_{i - 1}}}^{ - 1} + V{\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{A}}}&{ - V{\mathit{\boldsymbol{A}}^{\rm{H}}}}\\ { - V\mathit{\boldsymbol{A}}}&V \end{array}} \right]} \end{array} $ | (3) |
其中:
| $ \mathit{\boldsymbol{A}} = {\mathit{\boldsymbol{G}}_{k,{I_{i - 1}}}}\mathit{\boldsymbol{G}}_{{I_{i - 1}},{I_{i - 1}}}^{ - 1} $ | (4) |
| $ \begin{array}{*{20}{c}} {V = \frac{1}{{{\mathit{\boldsymbol{G}}_{k,k}} - {\mathit{\boldsymbol{G}}_{k,{I_{i - 1}}}}\mathit{\boldsymbol{G}}_{{I_{i - 1}},{I_{i - 1}}}^{ - 1}{\mathit{\boldsymbol{G}}_{{I_{i - 1}},k}}}} = }\\ {\frac{1}{{{\mathit{\boldsymbol{G}}_{k,k}} - A{\mathit{\boldsymbol{G}}_{{I_{i - 1}},k}}}}} \end{array} $ | (5) |
式中:k是当前选择的基向量的索引,GIi-1,Ii-1-1是第(i-1)次迭代得到的(i-1)×(i-1)逆矩阵,A是1×(i-1)的辅助向量,V是块矩阵广义逆的辅助标量。通过直接使用前一次迭代得到的GIi-1,Ii-1-1,GIi,Ii-1可以简化为矩阵乘法、矩阵加法和一个实数的倒数。因此,FBB的计算可以用之前迭代的计算结果来跳过GIi,Ii-1的计算。将Fi定义为第i次迭代中的最小二乘解矩阵,可分解为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_i} = {\mathit{\boldsymbol{F}}_{BB}} = \mathit{\boldsymbol{G}}_{{I_i},{I_i}}^{ - 1}\mathit{\boldsymbol{\varphi }}_{{I_i}}^{\rm{H}}{\mathit{\boldsymbol{F}}_{{\rm{opt}}}} = }\\ {\mathit{\boldsymbol{G}}_{{I_i},{I_i}}^{ - 1}{{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\varphi }}_{{I_{i - 1}}}}}&{{\mathit{\boldsymbol{\varphi }}_k}} \end{array}} \right]}^{\rm{H}}}{\mathit{\boldsymbol{F}}_{{\rm{opt}}}} = }\\ {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{G}}_{{I_{i - 1}},{I_{i - 1}}}^{ - 1} + \mathit{\boldsymbol{V}}{\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{A}}}&{ - \mathit{\boldsymbol{V}}{\mathit{\boldsymbol{A}}^{\rm{H}}}}\\ { - \mathit{\boldsymbol{VA}}}&\mathit{\boldsymbol{V}} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\varphi }}_{{I_{i - 1}}}^{\rm{H}}{\mathit{\boldsymbol{F}}_{{\rm{opt}}}}}\\ {\mathit{\boldsymbol{\varphi }}_k^{\rm{H}}{\mathit{\boldsymbol{F}}_{{\rm{opt}}}}} \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_{i - 1}} + \mathit{\boldsymbol{V}}{\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{A\varphi }}_{{I_{i - 1}}}^{\rm{H}}{\mathit{\boldsymbol{F}}_{{\rm{opt}}}} - \mathit{\boldsymbol{V}}{\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{\varphi }}_k^{\rm{H}}{\mathit{\boldsymbol{F}}_{{\rm{opt}}}}}\\ { - \mathit{\boldsymbol{VA\varphi }}_{{I_{i - 1}}}^{\rm{H}}{\mathit{\boldsymbol{F}}_{{\rm{opt}}}} + \mathit{\boldsymbol{V\varphi }}_k^{\rm{H}}{\mathit{\boldsymbol{F}}_{{\rm{opt}}}}} \end{array}} \right]} \end{array} $ | (6) |
其中M为1×Ns的辅助向量,如式(7)所示。
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{M}} = \mathit{\boldsymbol{A\varphi }}_{{I_{i - 1}}}^{\rm{H}}{\mathit{\boldsymbol{F}}_{{\rm{opt}}}} - \mathit{\boldsymbol{\varphi }}_k^{\rm{H}}{\mathit{\boldsymbol{F}}_{{\rm{opt}}}} = }\\ {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{\psi }}_0}\left( {{I_{i - 1}},:} \right) - {\mathit{\boldsymbol{\psi }}_0}\left( {k,:} \right)} \end{array} $ | (7) |
式中ψ0是基向量φ和初始残差矩阵Fres=Fopt的相关矩阵。因此,式(6)可以简化为
| $ {\mathit{\boldsymbol{F}}_i} = \left[ \begin{array}{l} {\mathit{\boldsymbol{F}}_{i - 1}} + \mathit{\boldsymbol{V}}{\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{M}}\\ - \mathit{\boldsymbol{VM}} \end{array} \right] $ | (8) |
综上所述,GIi,Ii-1、Fi和ψi都可以同时使用辅助变量(A,V,M)和前一次迭代的计算结果进行更新,进而替代矩阵求逆的过程,以减小计算量。
2.3 算法流程本文提出的算法将式(1)作为适应度函数,利用BSA算法来寻求式(1)的全局最优值和利用Banachiewicz-Schur分块矩阵广义逆,将高维度矩阵转换为低维度矩阵,避免矩阵求逆。算法流程具体如下。
算法:基于BSA的MIB-OMP混合预编码
输入:最优无约束预编码器为Fopt
输出:射频预编码器FRF;基带预编码器FBB
1) 初始化射频预编码矩阵FRF=[],残差矩阵Fres=Fopt;
2) 令i=1;
3) 根据式(1),利用BSA算法求出最优的阵列响应矢量w;
4) 将射频预编码矩阵FRF与阵列响应矢量w进行合并,即
| $ {\mathit{\boldsymbol{F}}_{{\rm{RF}}}} = \left[ {{\mathit{\boldsymbol{F}}_{{\rm{RF}}}}\left| w \right.} \right]; $ |
5) 根据式(4)、(5)、(7)分别计算A、V、M,进而利用式(3)得出GIi,Ii-1;
6) 根据式(8)更新基带预编码矩阵FBB;
7) 更新残差矩阵
8) 令i=i+1,若i≤NtRF,则返回第3)步,否则执行第9)步;
9) 对基带预编码矩阵进行归一化
为了验证本文提出的混合预编码算法的性能,本小节给出了在毫米波大规模MIMO系统下全数字预编码、模拟预编码、基于OMP的混合预编码和本文提出的算法的仿真结果,并进行对比分析。在仿真场景中,信道采用毫米波信道,群簇数Ncl=5,每个群簇的传播路径数Nray=10;天线阵列采用均匀线性阵列,并且方位角的AOA和AOD的簇角度在[0,2π)上服从均匀分布,角度扩展设为10°。仿真所得的结果都是在1 000次随机信道实现的平均。
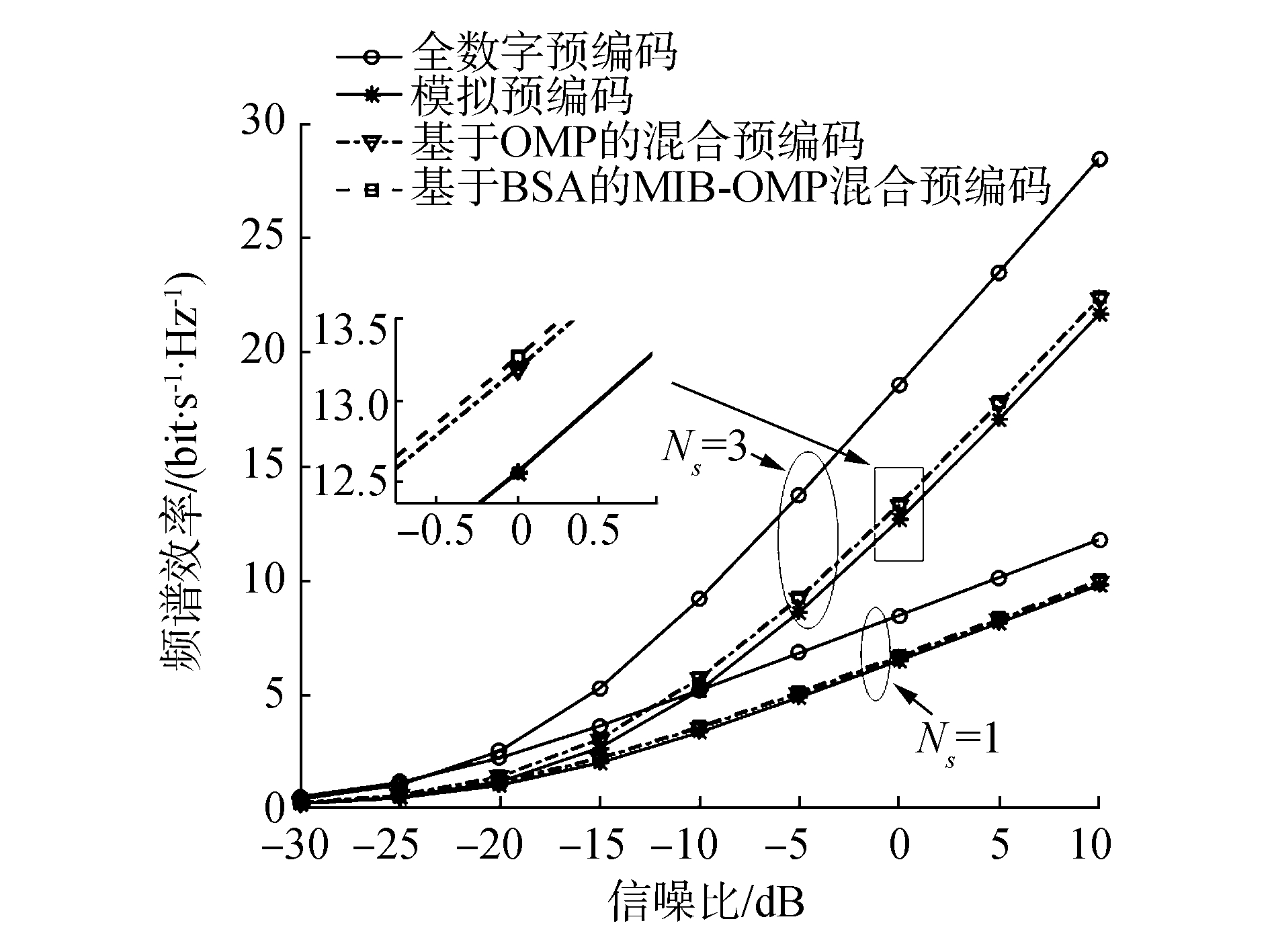
图 2给出了不同预编码在发射端配置Nt=64根天线、接收端配置Nr=16根天线、NRFt=NRFr=Ns=[1,3]的条件下,频谱效率随信噪比变化的曲线图。从图中可以看出,随着信噪比的增大,不同预编码的频谱效率都得到了不同程度的提升。而且随着数据流的增加,不同预编码的频谱效率也会得到不同程度的提升。对于不同的数据流,全数字预编码的性能最好,这是因为其是最优的预编码,所有的预编码都是以逼近它为目标。本文提出的算法与基于OMP的混合预编码性能基本相同,这是因为本文提出的算法仅对基于OMP的混合预编码的候选矩阵和矩阵求逆的问题进行改进,所以性能相近,但是仔细观察会发现本文提出的算法性能会有略微的提升,这是因为本文提出的算法采用BSA算法搜索全局最优解,而基于OMP的混合预编码则是使用候选矩阵选取相关度最大的一列,然而候选矩阵中每一列的角度会有间隔,所以选出来的阵列响应矢量不一定是全局最优解。模拟预编码性能最差,这是因为模拟预编码是恒模的,仅利用了相位的特点,并没有利用幅度的特点。因此,本文提出的算法在NRFt=NRFr=Ns条件下,能够达到比较好的效果。
|
Download:
|
| 图 2 NRFt=NRFr=Ns时不同预编码的频谱效率 | |
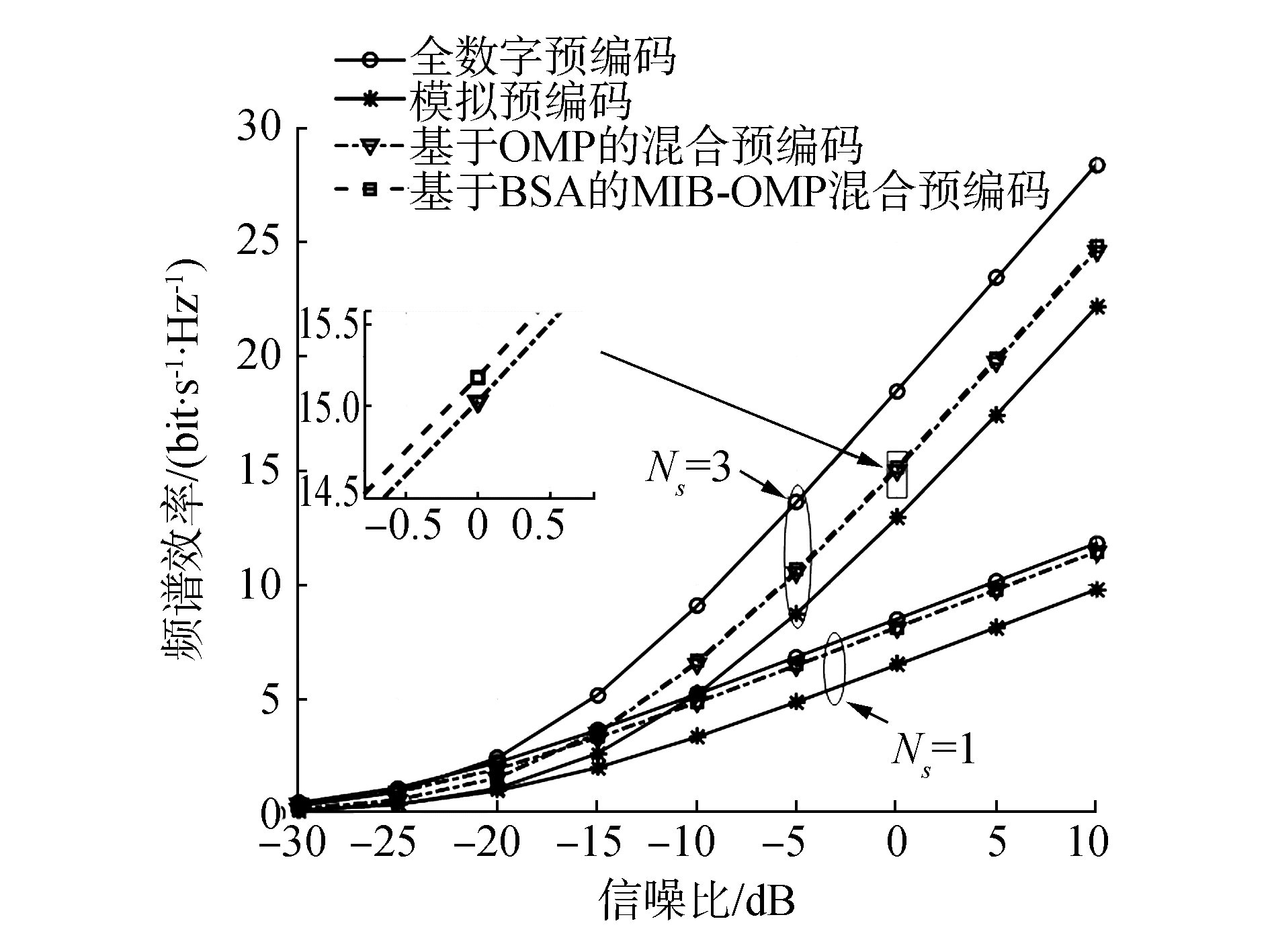
图 3给出了不同预编码在发射端配置Nt=64根天线、接收端配置Nr=16根天线、NRFt=NRFr=4、Ns=[1,3]的条件下,频谱效率随信噪比变化的曲线图。从图中可以看出,与图 2相同,随着信噪比和数据流的增大,不同预编码的频谱效率都得到不同程度的提升。同样的,对于不同的数据流,全数字预编码的性能最好,本文提出的算法与基于OMP的混合预编码性能基本相同,但是仔细观察会发现本文提出的算法性能会有略微的提升,模拟预编码性能最差。对比图 2和图 3可以发现,在NRFt=NRFr≥Ns情况下效果更好,这是因为在这种情况基带预编码和射频预编码的维度更高,预编码矩阵所含的信息更多,所以效果更好。因此,本文提出的算法在NRFt=NRFr≥Ns条件下,也能够达到比较好的效果。
|
Download:
|
| 图 3 NRFt=NRFr≥Ns时不同预编码的频谱效率 | |
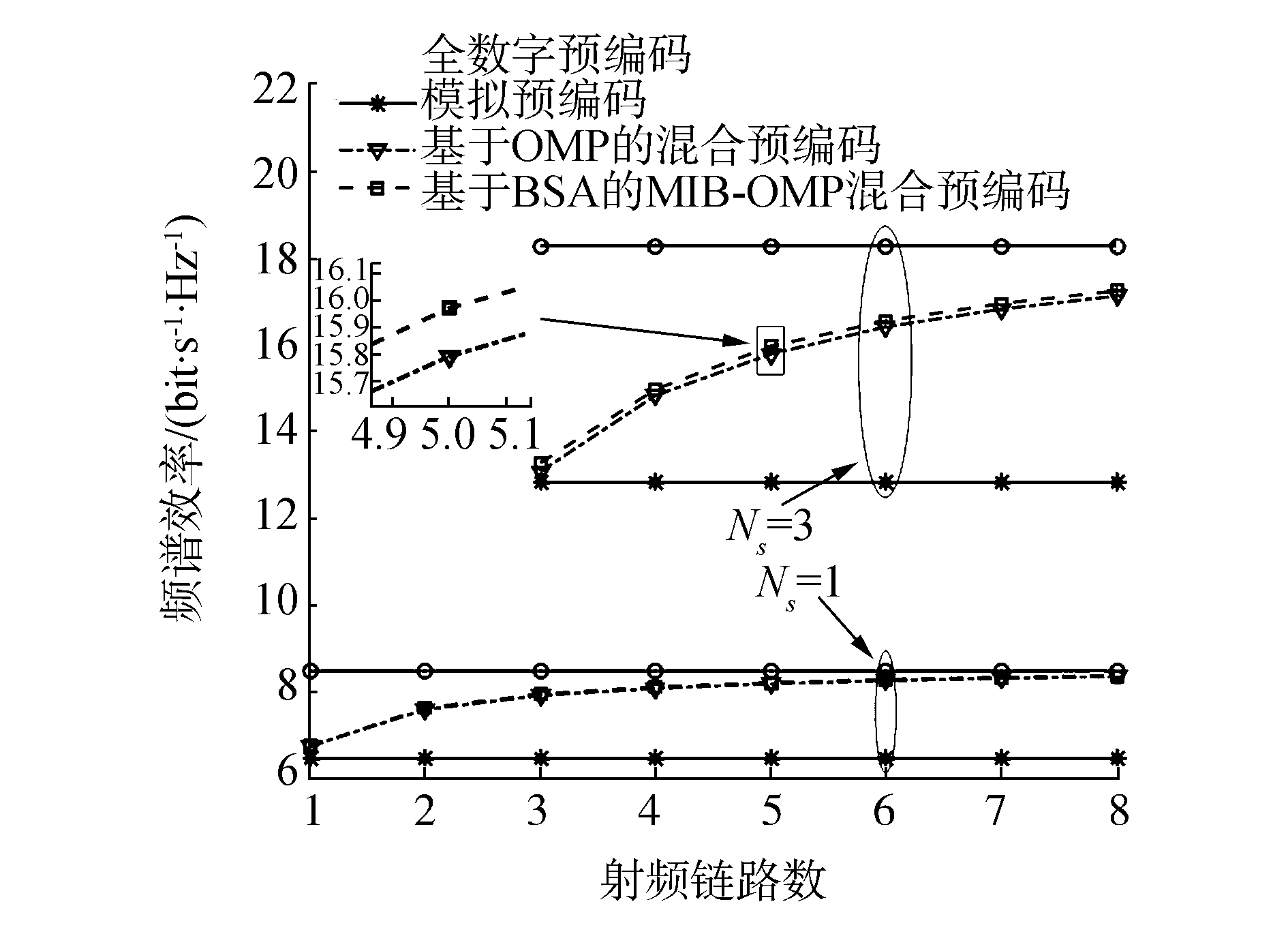
图 4给出了不同预编码在发射端配置Nt=64根天线、接收端配置Nr=16根天线、Ns=[1,3]、SNR=0 dB的条件下,频谱效率随射频链路数变化的曲线图。从图中可以看出,由于全数字预编码仅在基带进行预编码,模拟预编码仅在射频进行预编码,所以它们不受射频链路数变化的影响。随着射频链路数的增加,本文提出的算法和基于OMP的混合预编码的频谱效率都得到一定程度的提升,而且本文提出的算法略微优于基于OMP的混合预编码,其原因前面已经介绍过了,这里不再赘述。在Ns=1时,本文提出的算法和基于OMP的混合预编码在射频链路数为7时性能基本接近全数字预编码,而在Ns=3时,即使射频链路数为8也离全数字预编码有一定的差别。所以本文提出的算法和基于OMP的混合预编码特别适合射频链路数与数据流数差别比较大的情况,但是如果差别过大,就失去了混合预编码的意义,所以一般采用射频链路数是数据流数的2倍。因此,本文提出的算法在射频链路数不同时,也能达到比较好的效果。
|
Download:
|
| 图 4 频域脉冲压缩方法框图 | |
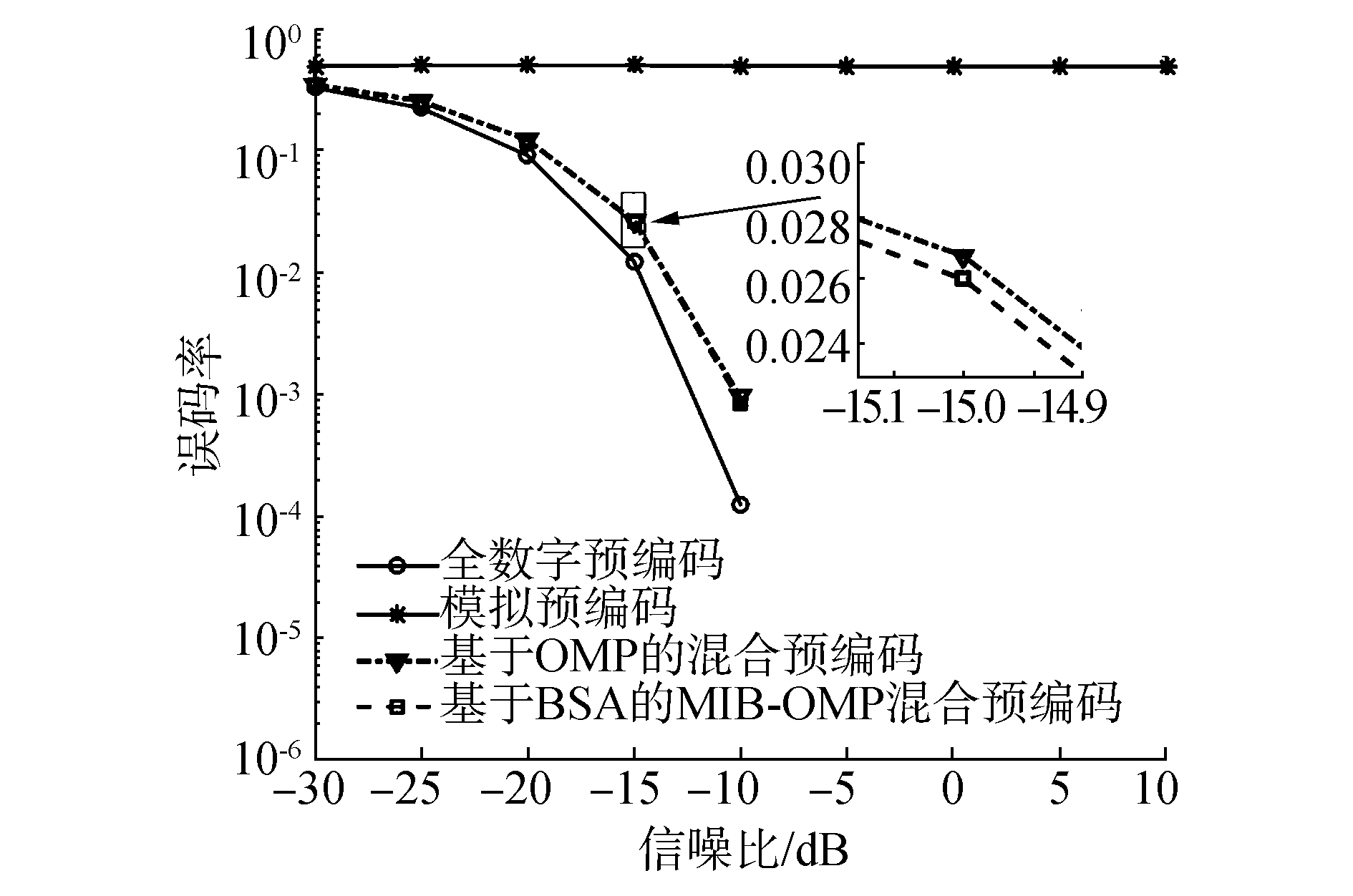
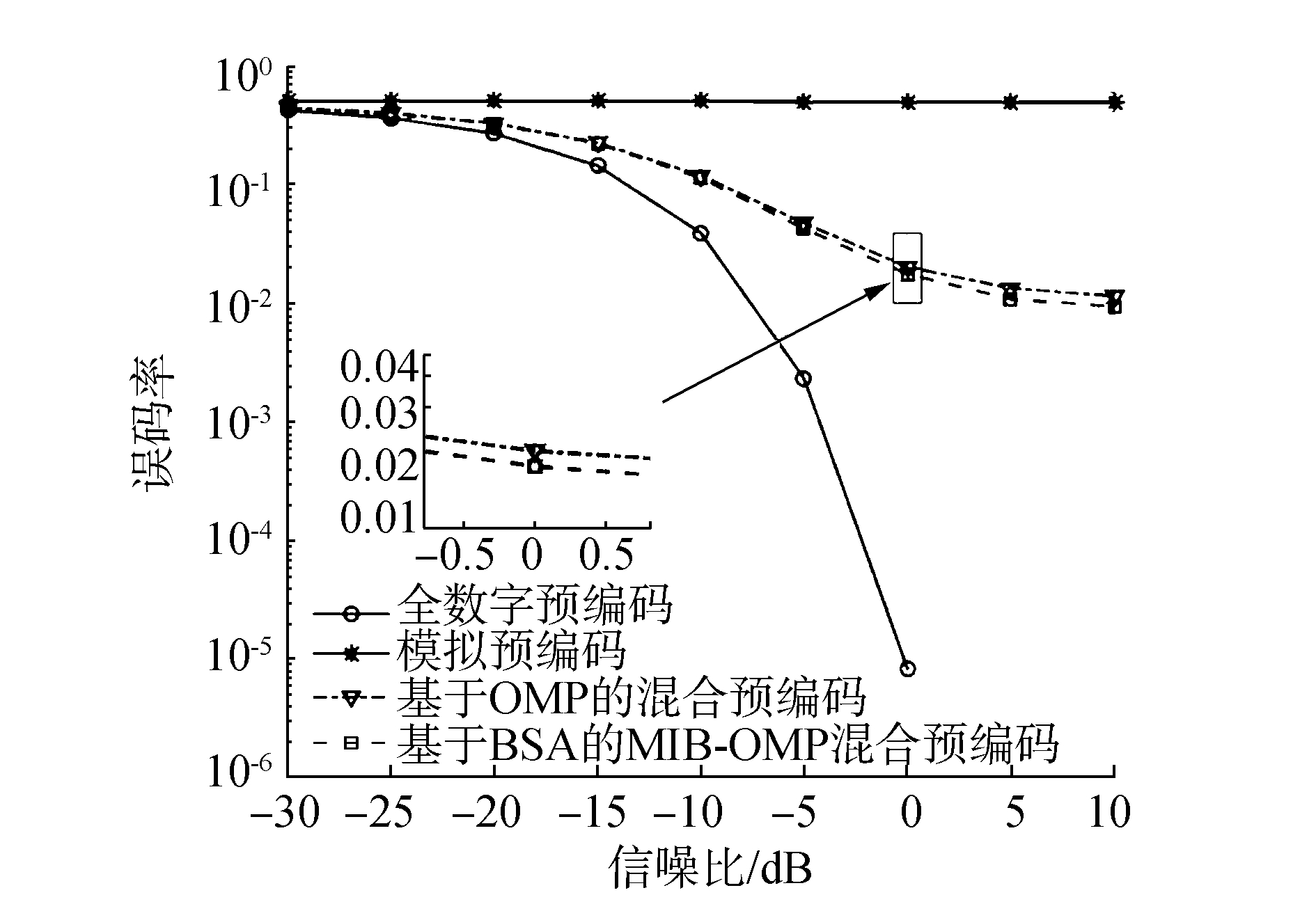
图 5、6给出了不同预编码在发射端配置Nt=64根天线、接收端配置Nr=16根天线、NRFt=NRFr=4、Ns分别在1和3时,误码率随信噪比变化的曲线图。从图 5、6可以看出,全数字预编码、基于OMP的混合预编码和本文提出的算法的误码率都随着信噪比的增大而减小,而模拟预编码保持不变,这是因为模拟预编码器选择的是信道增益最大的Ns列阵列响应矢量,它的选择与信噪比无关。对比图 5和图 6,可以发现,当Ns=1时,全数字预编码、基于OMP的混合预编码和本文提出的算法在-5 dB时已经达到最佳,即无误码率;当Ns=3时,全数字预编码在5 dB时可以达到最佳,而基于OMP的混合预编码和本文提出的算法,则在5 dB以后趋于平稳,而且仔细观察可以发现,本文提出的算法略优于基于OMP的混合预编码,这也与前边得出的结论不谋而合,即本文提出的算法和基于OMP的混合预编码特别适合射频链路数与数据流数差别比较大的情况。因此,本文提出的算法在误码率上也表现比较好的性能。
|
Download:
|
| 图 5 Ns=1、NRFt=NRFr=4时不同预编码的误码率 | |
|
Download:
|
| 图 6 Ns=3、NRFt=NRFr=4时不同预编码的误码率 | |
本文针对基于OMP的混合预编码存在需要已知候选矩阵和矩阵求逆的问题,提出了基于BSA的MIB-OMP混合预编码。该算法利用BSA具有全局搜索最优值的特点搜索与残差矩阵相乘内积最大的阵列响应矢量,同时利用Banachiewicz-Schur分块矩阵广义逆将高维度的矩阵转换为低维度的矩阵,避免矩阵求逆,减少计算量。与基于OMP的混合预编码相比,本文提出的算法在无需已知候选矩阵和矩阵求逆的条件下,系统频谱效率和误码率方面取得了更优的性能,但是本文算法的性能提升有限。因此,未来我们将围绕如何提升算法的性能的角度来进行预编码算法的研究。
| [1] |
赵绍刚, 李岳梦. 5G:开启未来无线通信创新之路[M]. 北京: 电子工业出版社, 2017.
( 0) 0)
|
| [2] |
HUANG Huang,LIU Kunpeng,WEN Rong,et al. Joint channel estimation and beamforming for millimeter wave cellular system[C]//2015 IEEE Global Communications Conference. San Diego,USA,2015: 1-6. https://www.researchgate.net/publication/301444242_Joint_Channel_Estimation_and_Beamforming_for_Millimeter_Wave_Cellular_System?_sg=-8x7g9U8fMLhCPb3nyo8WCmqMbCGcbadd08zaE9_VOHwJfzuywW_LU2LJHQeUDK44JmJkJ123DLK0L73pqstuA
( 0) 0)
|
| [3] |
苏昕, 曾捷, 粟欣, 等. 5G大规模天线技术[M]. 北京: 人民邮电出版社, 2017.
( 0) 0)
|
| [4] |
耿立茹.毫米波Massive MIMO系统中基于码本的波束管理研究[D].北京: 北京邮电大学,2018. http://cdmd.cnki.com.cn/Article/CDMD-10013-1018162137.htm
( 0) 0)
|
| [5] |
王明辉.毫米波大规模MIMO系统预编码技术研究[D].杭州: 杭州电子科技大学,2017. http://cdmd.cnki.com.cn/Article/CDMD-10336-1017133463.htm
( 0) 0)
|
| [6] |
SOHRABI F, YU Wei. Hybrid digital and analog beamforming design for large-scale antenna arrays[J]. IEEE journal of selected topics in signal processing, 2016, 10(3): 501-513. DOI:10.1109/JSTSP.2016.2520912 ( 0) 0)
|
| [7] |
AMADORI P V, MASOUROS C. Low RF-complexity millimeter-wave beamspace-MIMO Systems by beam selection[J]. IEEE transactions on communications, 2015, 63(6): 2212-2223. ( 0) 0)
|
| [8] |
ROWELL C,HAN Shuangfeng. Practical large scale antenna systems for 5G cellular networks[C]//2015 IEEE International Wireless Symposium. Shenzhen,China,2015: 1-4. https://www.researchgate.net/publication/308856623_Practical_Large_Scale_Antenna_Systems_for_5G_cellular_networks
( 0) 0)
|
| [9] |
HAN Shuangfeng, I C L, XU Zhikun, et al. Large-scale antenna systems with hybrid analog and digital beamforming for millimeter wave 5G[J]. IEEE communications magazine, 2015, 53(1): 186-194. DOI:10.1109/MCOM.2015.7010533 ( 0) 0)
|
| [10] |
HUR S, KIM T, LOVE D J, et al. Millimeter wave beamforming for wireless backhaul and access in small cell networks[J]. IEEE transactions on communications, 2013, 61(10): 4391-4403. DOI:10.1109/TCOMM.2013.090513.120848 ( 0) 0)
|
| [11] |
BRADY J, BEHDAD N, SAYEED A M. Beamspace MIMO for millimeter-wave communications:System architecture,modeling,analysis,and measurements[J]. IEEE transactions on antennas and propagation, 2013, 61(7): 3814-3827. DOI:10.1109/TAP.2013.2254442 ( 0) 0)
|
| [12] |
AYACH O E, RAJAGOPAL S, ABU-SURRA S, et al. Spatially sparse precoding in millimeter wave MIMO systems[J]. IEEE transactions on wireless communications, 2014, 13(3): 1499-1513. DOI:10.1109/TWC.2014.011714.130846 ( 0) 0)
|
| [13] |
RAPPAPORT T S, SUN Shu, MAYZUS R, et al. Millimeter wave mobile communications for 5G cellular:It will work![J]. IEEE access, 2013, 1: 335-349. DOI:10.1109/ACCESS.2013.2260813 ( 0) 0)
|
| [14] |
HUANG Guoxian,WANG Lei. High-speed signal reconstruction with orthogonal matching pursuit via matrix inversion bypass[C]//2012 IEEE Workshop on Signal Processing Systems. Quebec City,Canada,2012: 191-196. https://www.researchgate.net/publication/261484751_High-Speed_Signal_Reconstruction_with_Orthogonal_Matching_Pursuit_via_Matrix_Inversion_Bypass
( 0) 0)
|
| [15] |
MENG Xianbing, GAO X Z, LU Lihua, et al. A new bio-inspired optimisation algorithm:Bird Swarm Algorithm[J]. Journal of experimental & theoretical artificial intelligence, 2016, 28(4): 673-687. ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


