2. 西安航空职业技术学院 通用航空学院,陕西 西安 710089;
3. 西安市无人机应用创新基地,陕西 西安 710071
2. School of General Aviation, Xi'an Aerotechnical Polytechnic College, Xi'an 710089, China;
3. Xi'an UAV Application Innovation Base, Xi'an 710071, China
在控制领域,经典的PID控制方法以其明确的物理概念、对被控对象模型的高度适应性、简单的调参过程等优点,占据着工业控制的绝大部分领域。然而,随着被控对象越来越复杂,传统的PID控制方法也越来越暴露出其不足。根据相关实践,传统PID方法失效的根本原因并不在于被控对象的复杂程度,而是复杂系统所表现的非线性[1]。为了解决该问题,具有自主学习能力的智能控制方法得到了青睐。
从20世纪60年代开始,学习控制的思想成为了研究热点。智能控制方法可以根据被控对象的工作状态变化而调整控制器结构或者控制参数,通过自身的学习调整,来适应被控对象本身特性的改变[1−2]。这种自我学习和调整的能力,在处理大系统的非线性问题时表现出极大的优势。
对于智能算法而言,其出发点在于模仿自然界的生物行为或者人类自身的学习行为。其中,动物群体行为给了研究人员极大的启发,粒子群算法、蚁群算法、鱼群算法、遗传算法等等被广泛研究并得到应用。例如,文献[3]利用群智能优化技术分析大数据;文献[4]利用群智能优化解决网络覆盖优化问题;文献[5]利用群智能优化增强语音计算技术。
在这些算法的基础上,许多智能方法得到了极大的发展。针对控制方向未知的非线性时滞系统控制问题,文献[6]设计了一种鲁棒自适应学习控制算法;文献[7]提出了一种基于Page Rank的主动学习算法;文献[8]基于宽度学习方法提出了一个能够学习和融合两种模态特征的框架;文献[9]分析了宽度学习系统方法的数学理论和平层网络结构,并成功地应用于各种分类和回归任务中;文献[10]提出了一种针对特定问题的自动调整神经网络结构;文献[11]提出了一种基于行为主义的自组织多Agent系统智能控制与决策模型;文献[12]构建了一种基于多工序知识关联的纺纱质量智能控制模型。
作为自然界中学习能力最强的人类,其行为方式也成为研究者模拟的对象。借鉴人类的意识−情感−智能三位一体的思想,文献[13]设计并构建了供液系统的智能控制模型;文献[14]研究了Elman神经网络控制方法;文献[15−16]提出了一种主动学习算法并将其应用于图像分类领域;文献[17]提出了一种基于自组织模糊神经网络的溶解氧控制方法;文献[18]提出了基于卷积神经网络的多标记分类模型。
虽然这些方法具有很强的自学习和自我调整的能力,但是这些方法也存在着以下不足。首先,对于以神经网络为代表的自学习方法等,只能给出一个自我学习的网络结构,并不能得到精确的数学表达形式。另外,对于粒子群算法、蚁群算法、遗传算法等则需要漫长的迭代计算过程,很难满足工业应用的实时性要求。
针对这些问题,本文提出了一种模拟人类不同阶段学习的过程,并与传统PID控制方法相结合,得到了一种基于人类学习认知过程的PID控制方法。
1 人类学习认知过程建模人类对知识的学习是一种复杂的智能活动。从大的角度来说,主要有2种方式:继承式学习和自主式学习[1]。随着人们所处的年龄段、知识水平、环境因素等不同,这2种方式所占的比重也有所不同。继承式学习主要指通过周围人的传授、自主阅读、查找各种文献资料等方式获得已有的知识。而自主式学习主要指通过自身的实践、探索等方式获得相关知识。
对于获得知识来说,继承式学习和自主式学习是相互促进的。继承式学习可以快速、大量地获得被证明了的、现有的知识;在继承性学习的基础上,自主性学习才有迹可循。自主式学习是对继承式学习的一种延伸,可以反过来促进继承式学习。因此,这2种方式在数学表现上是一种乘积方式,而不是简单的线性叠加。人类这种获取知识的行为用数学模型表示为:
| $\Delta \omega (k) = \eta {\theta _{(k)}}{\vartheta _{(k)}}$ | (1) |
式中:
式(1)所示的学习认知模型,对于人们幼儿和儿童期的认知过程描述是合适的。在该阶段,早期人们对世界的认知几乎没有什么目的性。因此,这一阶段能够获得什么知识有着很大的随机性。这种认知上的随机性,是一个人全面认知社会的基础。不过,这对获得专业知识来说,显然是效率低下的。
但是,随着年龄的增长,特别是进入学校和走入社会的大部分阶段,人们学习都带有一定的目的性。例如,中小学阶段是在教师引导下,以获得较好的考试分数为目的(可能有偏颇)的学习过程;大学阶段是以获得感兴趣、符合自己职业规划的专业学习;工作阶段则是为了完成自己工作任务为牵引的学习活动。可以说,这些带有目的的学习过程放弃了随机学习的全面性,但是却极大地提高了对特定专业知识的学习效率。
对于这种带有目的性的学习过程,对模型式(1)做如下修正:
| $\Delta \omega (k) = \eta ({\varsigma _{(k)}} - {\theta _{(k)}}){\vartheta _{(k)}}$ | (2) |
式中
式(2)所示的模型不仅揭示了人们有目的学习认知的过程,还揭示了这些学习认知的效率。从式(2)可知,在初始阶段,由于继承式学习和目的相差甚远,人们可以快速地获得新的知识。然而,随着继承式学习认知不断向目的靠近,学习效率也在不断地降低,直至和目的重合,无法获得新的知识。
对于大多数人来说,模型式(1)和(2)已经可以完整地描述其学习认知过程。但是,对于一些从事具有创造性的人来说,模型式(2)依然有着不足。对于具有创造性需求的人士来说,不仅仅要盯着当前的工作进行有目的的学习认知,还会不断地丰富自身的知识宽度和边界,以便更好地了解所处的世界。在更加深入了解所处世界的基础上,对自身的知识结构进行反馈优化,甚至进行自主式独立探索。对于这类人士的学习、认知过程,这里用如下方式来描述:
| $\Delta \omega (k) = \eta ({\varsigma _{(k)}} - {\theta _{(k)}}){\theta _{(k)}}{\vartheta _{(k)}}{\vartheta _{(k)}}$ | (3) |
控制是一种有着明确目的性的调节过程。本文的目的就是在充分认识人类学习认知的基础上,使得控制器具有自学习、自调节的能力,从而更好地完成控制目的。
对于一个控制系统来说,如果系统的输出状态为
| $e(t) = {x_r}(t) - x(t)$ |
对于该系统,传统的PID控制器形式为
| $u(t) = {k_{\rm{P}}}e(t) + {k_{\rm{I}}}\smallint e(t){\rm d}t + {k_{\rm{D}}}\dot e(t)$ | (5) |
把上述控制器写成增量形式为
| $\begin{array}{l} \Delta u(k) = {k_{\rm{P}}}(e(k) - e(k - 1)) + {k_{\rm{I}}}e(k) + \\ \;\;\;\;\;\;\;\;\;\;\;\;{k_{\rm{D}}}\displaystyle\frac{{e(k) - 2e(k - 1) + e(k - 2)}}{{\Delta t}} \end{array}$ |
则式(4)所示的控制器的增量表示为
| $u(k) = u(k - 1) + \Delta u(k)$ | (7) |
为了实现控制器参数的自整定、自学习能力,将式(5)表示成如下形式:
| $u(k) = u(k - 1) + K\sum\limits_{i = 1}^3 {{\omega _i}(k){x_i}(k)} $ |
式中:x1(k) = e(k),x2(k) = e(k)−e(k−1),x3(k) = e(k)−2e(k−1)+e(k−2);K为比例系数;ωi为学习认知获得知识。
这里采用式(3)所示的人类学习认知模型来实现控制器参数的自学习和自整定。则控制器参数学习规则如下所示:
| ${\omega _1}(k) = {\omega _1}(k - 1) + {\eta _{\rm I}}e(k)u(k)x_1^2(k)$ |
| ${\omega _2}(k) = {\omega _2}(k - 1) + {\eta _{\rm P}}e(k)u(k)x_2^2(k)$ |
| ${\omega _3}(k) = {\omega _3}(k - 1) + {\eta _{\rm D}}e(k)u(k)x_3^2(k)$ |
式中
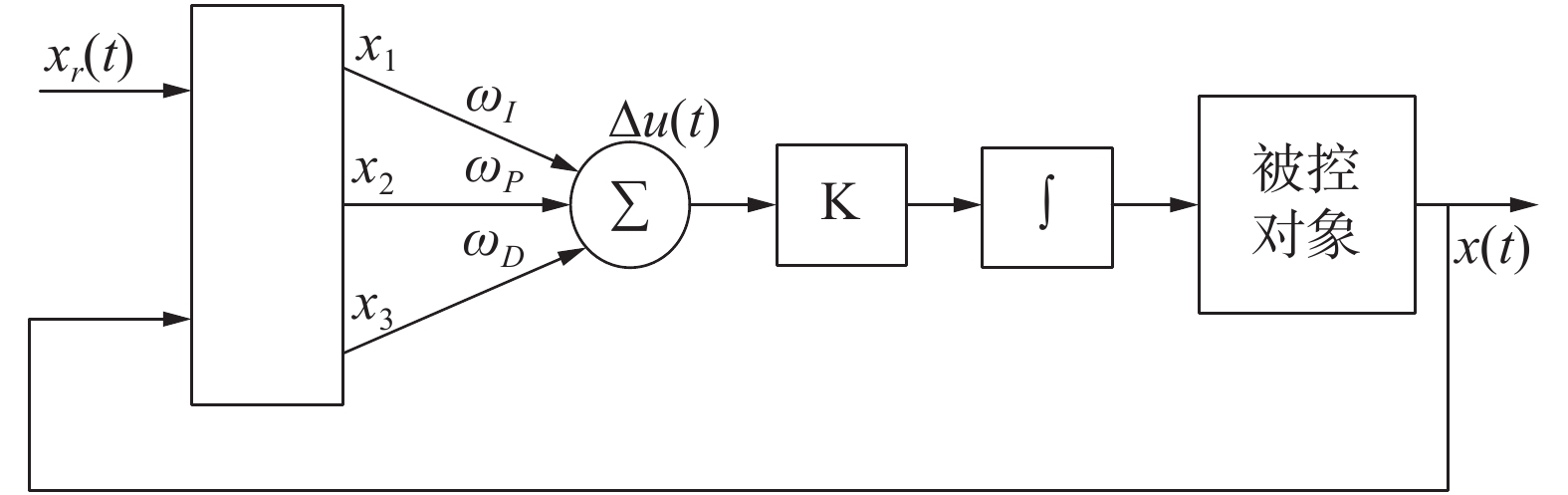
该基于人类学习认知模型的控制器模型,其控制器结构如图1所示。
|
Download:
|
| 图 1 基于人类学习认知模型的控制器结构 | |
对于某被控对象可表示为如下形式的三阶差分模型:
| $\begin{aligned}{l} x(k) = 0.3x(k - 1) + 0.2x(k - 2) + 0.026{\kern 1pt} {\kern 1pt} x(k - 3) + \\ 0.1u(k - 1) + 0.623u(k - 2)\qquad\qquad\qquad \end{aligned}$ |
接下来将用本文设计方法来验证该被控对象对方波和正弦波的跟踪情况。
3.1 对方波信号的跟踪若系统要跟踪的理想输入信号为
| ${x_d} = 0.2{\rm{sign}}(\sin (6{\rm{{\text π} }}t))$ |
设定控制器的初始参数分别为p=0.05、i=0.1、
|
Download:
|
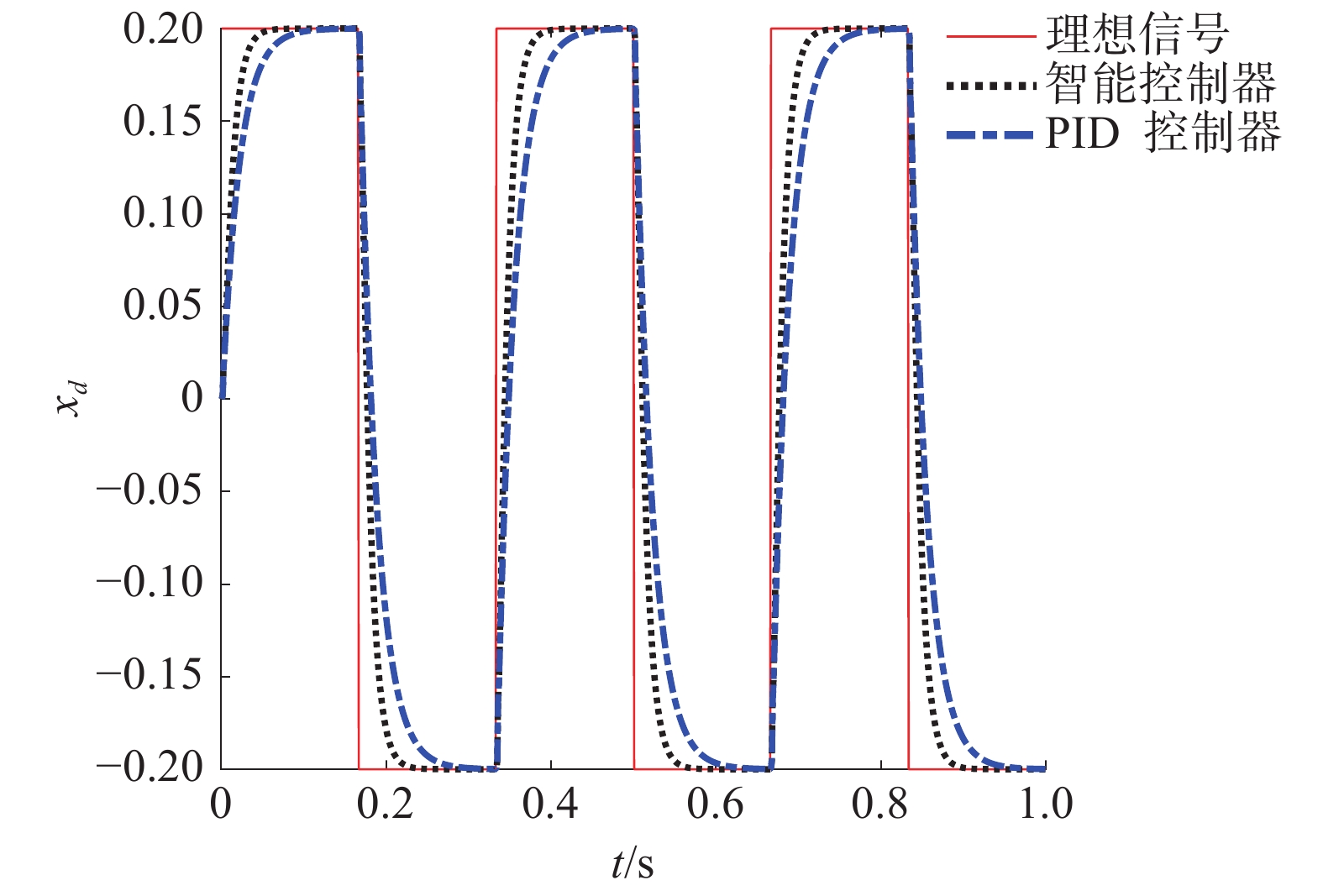
| 图 2 系统对方波信号的跟踪 | |
从图2可知,本文所设计的智能PID控制器可以快速跟上理想方波信号,而且没有超调和稳态误差现象的出现。和传统PID控制器相比,本文方法具有更快的响应速度。仿真结果证明了本文方法设计得到的控制器具有很好的性能。
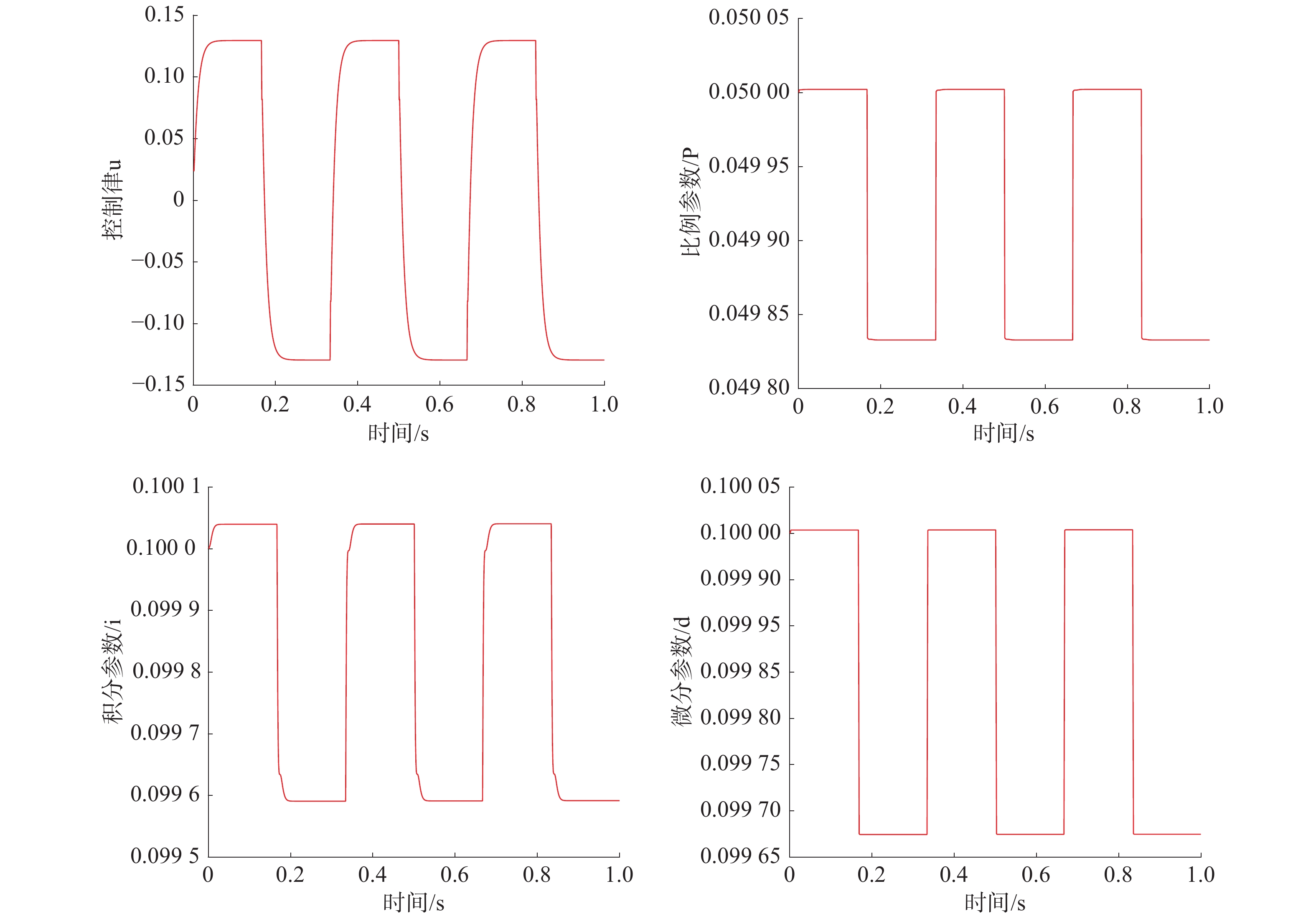
控制过程中控制器输入和控制器参数调节过程如图3如所示。
|
Download:
|
| 图 3 控制器输入和控制器参数调节过程 | |
从图3可知,在控制过程中,控制器的控制输入和控制器参数在自学习中不断进行优化,使得控制器具有最好的控制效果。
3.2 对正弦信号的跟踪若系统要跟踪的理想输入信号为
| ${x_d} = \sin (5{\rm{{\text π}}}t)$ |
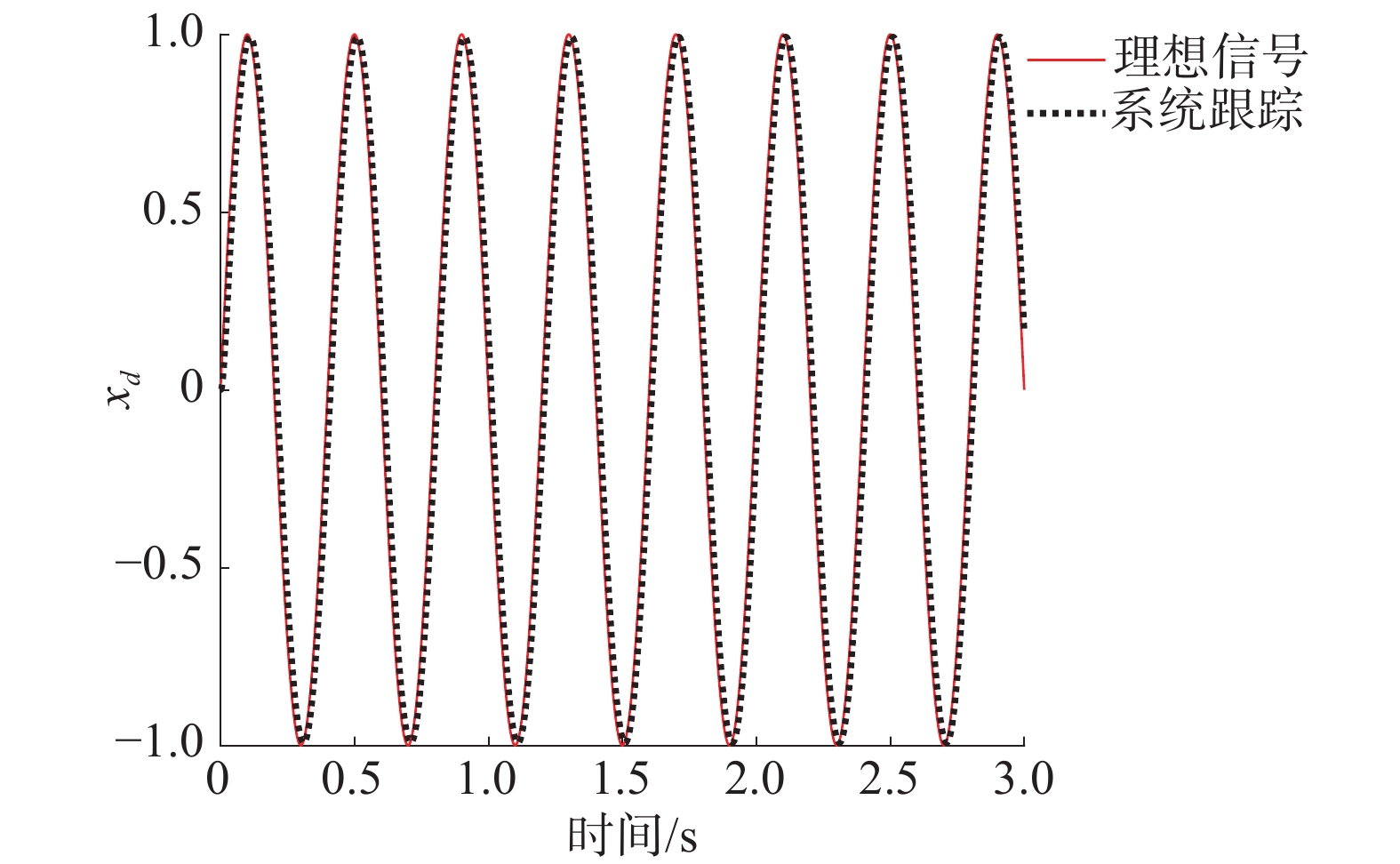
设定控制器的初始参数为随机数。被控对象对理想信号的跟踪结果如图4所示。从图4可知,系统可以精确、快速跟上理想正弦信号,而且没有相位延迟的出现。说明控制器具有很好的性能。控制器输入和控制器参数调节过程如图5所示。
|
Download:
|
| 图 4 系统对正弦信号的跟踪 | |

|
Download:
|
| 图 5 控制器输入和控制器参数调节过程 | |
从图5可知,控制器的控制输入和控制器参数同样具有自我学习和调整的过程。
4 结论本文针对传统PID方法在对复杂系统控制时,对非线性问题处理不足的缺点,提出了一种基于人类学习认识模型的智能PID控制方法。
1)本文在分析人类不同年龄阶段学习过程的基础上,建立了人类学习认知模型,并应用该模型设计了一种可以在线自主调参的PID控制器;
2)本文所设计的控制器不仅具有针对复杂系统非线性特点的处理能力,而且克服了大多数智能方法计算迭代复杂、没有数学解析模型的缺点;
通过对方波信号和正弦信号进行跟踪仿真实验,结果表明,文中所设计的控制器具有很好的控制效果。
| [1] |
黄琳, 杨莹, 李忠奎. 关于智能控制的几个问题[J]. 中国科学: 信息科学, 2018, 48(8): 1112-1120. ( 0) 0)
|
| [2] |
王飞跃, 魏庆来. 智能控制: 从学习控制到平行控制[J]. 控制理论与应用, 2018, 35(7): 939-948. ( 0) 0)
|
| [3] |
CHENG Shi, ZHANG Qingyu, QIN Quande. Big data analytics with swarm intelligence[J]. Industrial management & data systems, 2016, 116(4): 646-666. ( 0) 0)
|
| [4] |
XIA Junbo. Coverage optimization strategy of wireless sensor network based on swarm intelligence algorithm[C]//2016 International Conference on Smart City and Systems Engineering. Changsha, China: IEEE, 2017: 179-182.
( 0) 0)
|
| [5] |
DEVI K U, SARMA D, LAISHRAM R. Swarm intelligence based computing techniques in speech enhancement[C]//2015 International Conference on Green Computing and Internet of Things. Noida, India: IEEE, 2015: 1199-1203.
( 0) 0)
|
| [6] |
陶洪峰, 沈建强, 陈刚, 等. 非线性时滞系统的未知方向自适应学习控制[J]. 控制工程, 2017, 24(6): 1170-1174. ( 0) 0)
|
| [7] |
邓思宇, 刘福伦, 黄雨婷, 等. 基于Page Rank的主动学习算法[J/OL]. 智能系统学报: (2018-06−27)[2018-08−20]. http://kns.cnki.net/kcms/detail/23.1538.TP.20180627.1529.002.html. DOI: 10.11992/tis.201804052.
( 0) 0)
|
| [8] |
贾晨, 刘华平, 续欣莹, 等. 基于宽度学习方法的多模态信息融合[J/OL]. 智能系统学报: (2018-05−22)[2018-08−20]. http://kns.cnki.net/kcms/detail/23.1538.TP.20180522.1345.002.html. DOI: 10.11992/tis.201803022.
( 0) 0)
|
| [9] |
CHEN C L P, LIU Zhulin. Broad learning system: an effective and efficient incremental learning system without the need for deep architecture[J]. IEEE transactions on neural networks and learning systems, 2017, 29(1): 10-24. ( 0) 0)
|
| [10] |
HABBI H, BOUDOUAOUI Y, KARABOGA D, et al. Self-generated fuzzy systems design using artificial bee colony optimization[J]. Information sciences, 2015, 295: 145-159. DOI:10.1016/j.ins.2014.10.008 ( 0) 0)
|
| [11] |
杨斯博, 李敏强. 一个基于自组织多Agent系统的智能控制与决策模型[J]. 天津大学学报, 2012, 45(10): 903-911. ( 0) 0)
|
| [12] |
邵景峰, 马创涛. 一种多工序知识关联的纺纱质量智能控制模型[J]. 控制理论与应用, 2018, 35(6): 840-851. ( 0) 0)
|
| [13] |
付翔, 王然风. 基于意识−情感−智能三位一体的煤矿供液过程控制[J]. 智能系统学报, 2018, 13(4): 640-649. ( 0) 0)
|
| [14] |
王鑫, 贾涛, 闻新. Elman神经网络控制与LQR的实践与分析[J]. 工业控制计算机, 2018, 31(3): 81-82. DOI:10.3969/j.issn.1001-182X.2018.03.034 ( 0) 0)
|
| [15] |
WANG Min, MIN Fan, ZHANG Zhiheng, et al. Active learning through density clustering[J]. Expert systems with applications, 2017, 85: 305-317. DOI:10.1016/j.eswa.2017.05.046 ( 0) 0)
|
| [16] |
SUN Shujin, ZHONG Ping, XIAO Huaitie, et al. An MRF model-based active learning framework for the spectral-spatial classification of hyperspectral imagery[J]. IEEE journal of selected topics in signal processing, 2015, 9(6): 1074-1088. DOI:10.1109/JSTSP.2015.2414401 ( 0) 0)
|
| [17] |
许进超, 杨翠丽, 乔俊飞, 等. 基于自组织模糊神经网络溶解氧控制方法研究[J]. 智能系统学报, 2018, 7(1): 1-7. ( 0) 0)
|
| [18] |
余鹰, 王乐为, 吴新念, 等. 基于改进卷积神经网络的多标记分类算法[J/OL]. 智能系统学报: (2018-06−10)[2018-08−20]. http://kns.cnki.net/kcms/detail/23.1538.TP.20180610.2155.002.html. DOI: 10.11992/tis.201804056.
( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


