现阶段陆上资源日益稀少,采集成本越来越高昂,人类将目光逐渐移向海洋。海洋资源总量丰富,长期以来,由于人类科学技术条件的限制,始终无法将海洋中的资源变现。随着计算机水平的发展,进入21世纪以来,有条件的大国都将海洋战略列入国家发展规划中,以无人水下机器人为主体的海洋探测越来越频繁,有人预言,未来的海底必是人类经常踏入的热土[1]。
现有的无人水下机器人大多采用传统的螺旋桨推进方式,伴有较大的噪音和尾涡。这对水下潜器来说都是负面的影响,此时仿生学的概念被大量提起。鱼类经过上亿年的进化,无论是身体形态结构还是运动方式都完美适应了环境。相比于螺旋桨推进系统的种种缺陷,仿鱼类水下潜器有良好的推进性能和操纵性能,可以高速游动并且姿态也可以随意控制,因此,比传统推进器具有更大优势的仿生推进器成为推进领域中的一个研究热点[2−3]。
1971年,Lighthill[4]提出了“大摆动细长体理论”,考虑了尾翼任意摆动幅度的运动,侧向位移较大,并对鱼的运动状态进行了分析。在1977年,Chopra等[5]提出了一种可用于摆动和新月形尾鳍推进系统的“二维抗力理论”,在理论上,尾鳍和摆动运动被充分考虑,并分析了任意摆动的规则或不规则运动,得到了推动力的表达式、维持运动所需的螺旋桨功率等,并指出水动力效率是斯特罗哈尔数(St数)、振幅的函数。
Wu[6]在1961年提出了二维波板理论,在这个理论中,鱼的身体被认为是一个弹性薄板,然后利用二维波片理论研究鱼体的变速运动。在20世纪80年代,中国科技大学的童秉刚等[7]建立了3D WPT理论,运用这一理论对不同种类鱼类的泳姿进行研究,以选择最佳的推进方式。在此期间,他们加入边界层来分析基于半解析理论的大摆幅运动问题。
摆翼理论主要用于解决鱼类在尾鳍推进模式下的运动问题。这种鱼的运动基本上依靠尾鳍产生推力,尾鳍摆动相对较大。该理论将尾鳍运动分为2种:平移运动和旋转运动,利用表面单元法对二维或三维水翼进行分析。升力线和升力面理论经常被用于摆动翼理论,常采用准稳态升力线理论对鱼尾鳍进行水动力分析。Chopra[8]应用非定常升力面理论对不同形状的机翼进行分析,发现新月形尾翼的性能最优。苏玉民[9]采用表面单元法计算三维刚性尾鳍的流体动力特性,讨论了运动参数对尾鳍水动力性能的影响。梁建宏等[10]通过实验研究了在不同频率下,仿鱼推进器的游动速度、阻力与消耗功率的关系,通过观测流场,发现了鱼体前缘涡和尾鳍后形成的反卡门漩涡阵列与推进有重要关系。Q.Zhu[11]采用三维非定常面元法研究金枪鱼的运动,研究鱼尾对流场产生的涡流的影响,指出了鱼可以利用流场中的旋涡来提高推进效率。国外对仿生推进的摆动翼理论开展了较多的研究工作,取得了许多定性和定量的结果。1994年,美国麻省理工学院的M.S.Triantafyllou等[12]尝试主动控制尾鳍摆动时产生的尾流,尾鳍摆动时产生的尾流是一系列方向交错排列、离散的漩涡,他们认为,尾鳍摆动时可以从尾流中回收能量,而这正是采用鲹科加新月形尾鳍模式推进的鱼类推进效率高的主要因素之一。
1 理论基础 1.1 基本方程从物理学的概念来看,流体运动(包括层流、湍流)并没有什么特别的地方,它完全符合物理学三大定律:质量守恒定律、动量定律和能量守恒定律。所以,描述流体的运动基本方程式只是这3个物理学定律的数学表达形式[13]。
描述黏性流体运动的微分形式的基本方程组为:
| $ \left\{ \begin{aligned} & \frac{{\partial \rho }}{{\partial t}} + \nabla (\rho V) = 0 \\ & \frac{{\partial (\rho V)}}{{\partial t}} + \nabla (\rho VV) = \rho {{f - }}\nabla p + \nabla \tau \\ & \mathop c\nolimits_p \left[ {\frac{{\partial (\rho T)}}{{\partial t}} + \nabla (\rho VT)} \right] = \frac{{Dp}}{{Dt}} + \varphi + \nabla \& (k\nabla T) + S \\ & p = \rho RT \end{aligned} \right.$ |
式中:
| $\varphi = \nabla (\tau \cdot V) - (\nabla \tau )\cdot V$ |
动力黏性系数为常数且满足牛顿内摩擦定律的流体称为牛顿流体,对于牛顿流体的切向力和变形速率,有:
| $ \left\{ \begin{aligned} & \tau = - \frac{2}{3}\mu (\nabla V)I + 2\mu S\\ & S = \frac{1}{2}\left[ {{{(\nabla V)}_c} + (\nabla V)} \right] \end{aligned} \right. $ |
本文的研究不涉及换热现象,因此不考虑能量方程,而状态方程采用理想气体的状态方程来表达,则简化后的方程为:
| $ \left\{ \begin{aligned} & \nabla V = 0 \\ & \frac{{\partial V}}{{\partial t}} + V \cdot \nabla V = {{f}} - \frac{1}{\rho }\nabla p + \frac{1}{\rho }\nabla \tau \\ \end{aligned} \right. $ |
式中
本文中采用的是SST
| $ \left\{ \begin{aligned} & \frac{{\partial k}}{{\partial t}} + {u_i}\frac{{\partial k}}{{\partial {x_i}}} = \frac{1}{\rho }{P_k} - {\beta '}k\omega +\frac{1}{\rho }\frac{\partial }{{\partial {x_i}}}\left[ {\left( {{\mu _i} + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial t}}} \right] \\ & \frac{{\partial \omega }}{{\partial t}} + {u_i}\frac{{\partial \omega }}{{\partial {x_i}}} = \frac{1}{\rho }{P_\omega } - \beta {\omega ^2} + \\ & \quad \quad \frac{1}{\rho }\frac{\partial }{{\partial {x_i}}}\left[ {\left( {{\mu _i} + \frac{{{\mu _t}}}{{{\sigma _\omega }}}} \right)\frac{{\partial \omega }}{{\partial {x_i}}}} \right] + 2(1 - {F_1})\sigma {\omega _2}\frac{1}{\omega }\frac{{\partial k}}{{\partial {x_i}}}\frac{{\partial \omega }}{{\partial {x_i}}} \\ \end{aligned} \right. $ |
式中:
模型的漩涡性系数为:
| ${\mu _t} = \min \left[ {\frac{{\rho k}}{\omega }, \frac{{{a_1}\rho k}}{{\varOmega {F_2}}}} \right]$ |
模型控制方程中的一些常数为:
| $\varphi = {F_1}{\varphi _1} + \left( {1 - {F_1}} \right){\varphi _2}$ |
本文所用的摆动水翼模型如表1所示。选取的翼型为NACA0012翼型,相对宽度为12%。
|
|
表 1 摆动翼型主要几何参数 |
如图1所示,根据自然界中鱼类游动的环境,流体域被建立成一个方体,来模拟无穷边界的大海,其中包含摆动水翼及附近流体。建立如下坐标系:以摆动水翼的中心点为坐标原点;x轴正向为入射水流方向;z轴通过摆动水翼的中心点,且与展长方向一致;y轴方向由x轴和z轴确定。因为摆动水翼是在流体域中做运动,因此摆动水翼的周围建立了一个小域,应用重叠网格创建交界面;另外,摆动水翼后的尾流场是需要重点观察的对象,因此在摆动水翼后建立一个长方体域,以上两个小域内部布置密集的网格,而在其他计算域内布置较稀疏的网格。

|
Download:
|
| 图 1 整体计算域和网格示意 | |
本文采用全结构化网格技术,划分的摆动水翼的网格图见图2。

|
Download:
|
| 图 2 摆动水翼表面网格 | |
大域与小域的交界面处对网格进行适当加密,大域的网格如图3所示。对于结构化网格,分割的网格越接近于正方体,其奇异性越好。从图3中可以看出,摆动翼周围和尾流域网格较密,且网格分布均匀,网格大小适中;在远离摆动水翼的流体域内网格较为稀疏,整体网格十分规则。

|
Download:
|
| 图 3 纵截面网格 | |
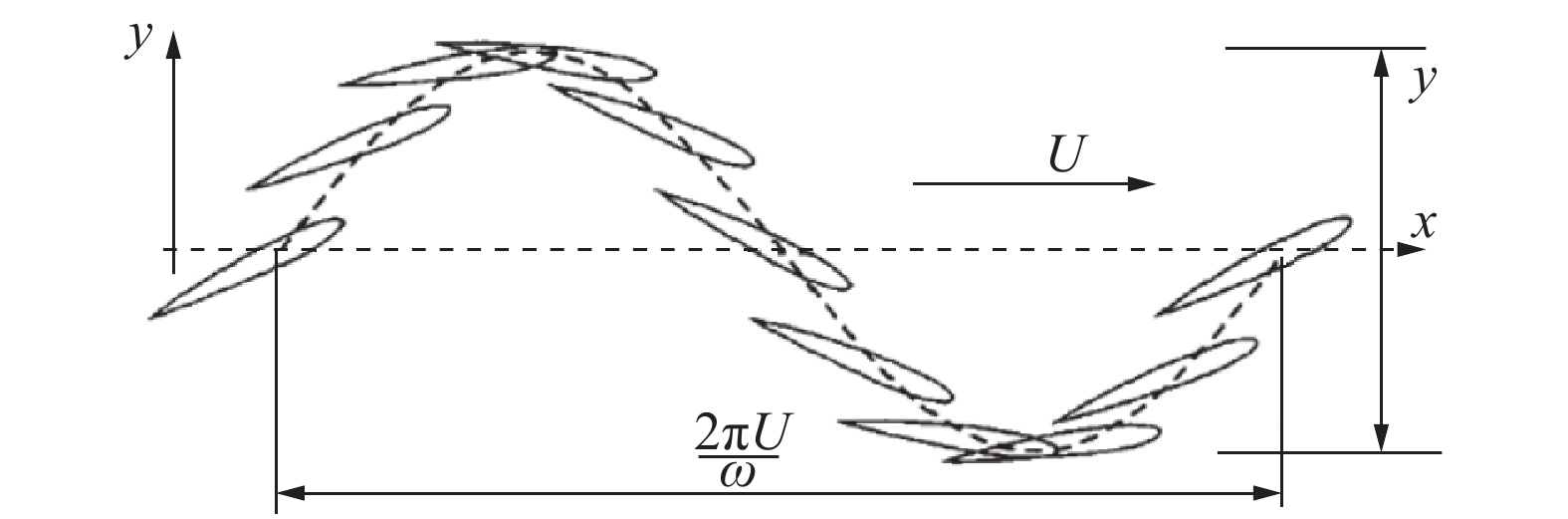
整个流体大域的入口处设为速度入口,出口处设置为压力出口,其他的边界都设置为壁面。流体域的水流速度设置为0.4 m/s,速度沿着x轴正向。摆动翼的运动分为2个运动,一个是水翼沿y轴方向的升沉运动,一个是绕z轴旋转的俯仰运动,旋转轴位于距水翼头部0.3倍弦长处[15],运动状态如图4所示。
|
Download:
|
| 图 4 摆动水翼运动示意 | |
摆动水翼的运动为升沉运动和俯仰运动的耦合运动,其数学表达式为:
| $ \left\{ \begin{aligned} & y\left( t \right) = {y_0}\cos \left( {wt} \right) \\ & \theta \left( t \right) = {\theta _0}\cos \left( {wt{\rm{ + }}\phi } \right) \\ \end{aligned} \right. $ |
式中:
本文所要研究的摆动翼,在水中的运动是一个非定常的周期性运动。对于非定常的周期性运动,通常采用相似准数St数来反映水动力情况,St数是局部惯性力与对流惯性力量级之比,在本文中表示为:
| $S \!\! t = \frac{{fA}}{U}$ |
式中:U为来流速度;A为尾流的宽度,其大小取为摆动翼做升沉运动最大幅值的二倍。
在本文中,流场中Re数保持不变,意味着流体流速U是恒定值;另外
如图5所示,这是t=5 s时刻不同St数下的压力分布图,由于不同St数下摆动翼的周期不同,因此此时摆动翼的运动姿态是不同的。从这4张图中可以看出翼型上部和下部的压力是不同的,这是由于摆动翼具有上下运行的平移速度,摆动翼向上运动时,对翼型上部流体形成挤压作用,因此上部流体压力更大;同时对翼型下部流体形成吸引作用,因此下部流体压力较小。在压力云图上显示为翼型上部为红色,下部为深蓝色;摆动翼向下运动时,翼型上部为深蓝色,下部为红色。

|
Download:
|
| 图 5 摆动翼水翼表面压力分布 | |
另一个明显的现象是深红色区域集中分布于摆动翼的头部或尾部,这是由于摆动翼在做升沉运动的同时,也在绕垂直于平面截面的某个轴进行俯仰运动,因此在摆动翼头部或者尾部有比旋转点更高的速度,并且还由于压力中心在头部生成,在尾部脱落形成尾涡,这就使得头部和尾部承受了更大的流体压力。
3.2 力的曲线如图6所示,推力曲线都是正弦三角函数分布,这与本文中设置的运动有关。摆动翼的运动函数也表示为正弦或余弦三角函数,并且推力的最大值都在零附近,这是因为本文中将初始位置设置在了摆动翼运行的最高位置处,此处摆动翼所受推力为零。

|
Download:
|
| 图 6 摆动水翼所受推力曲线 | |
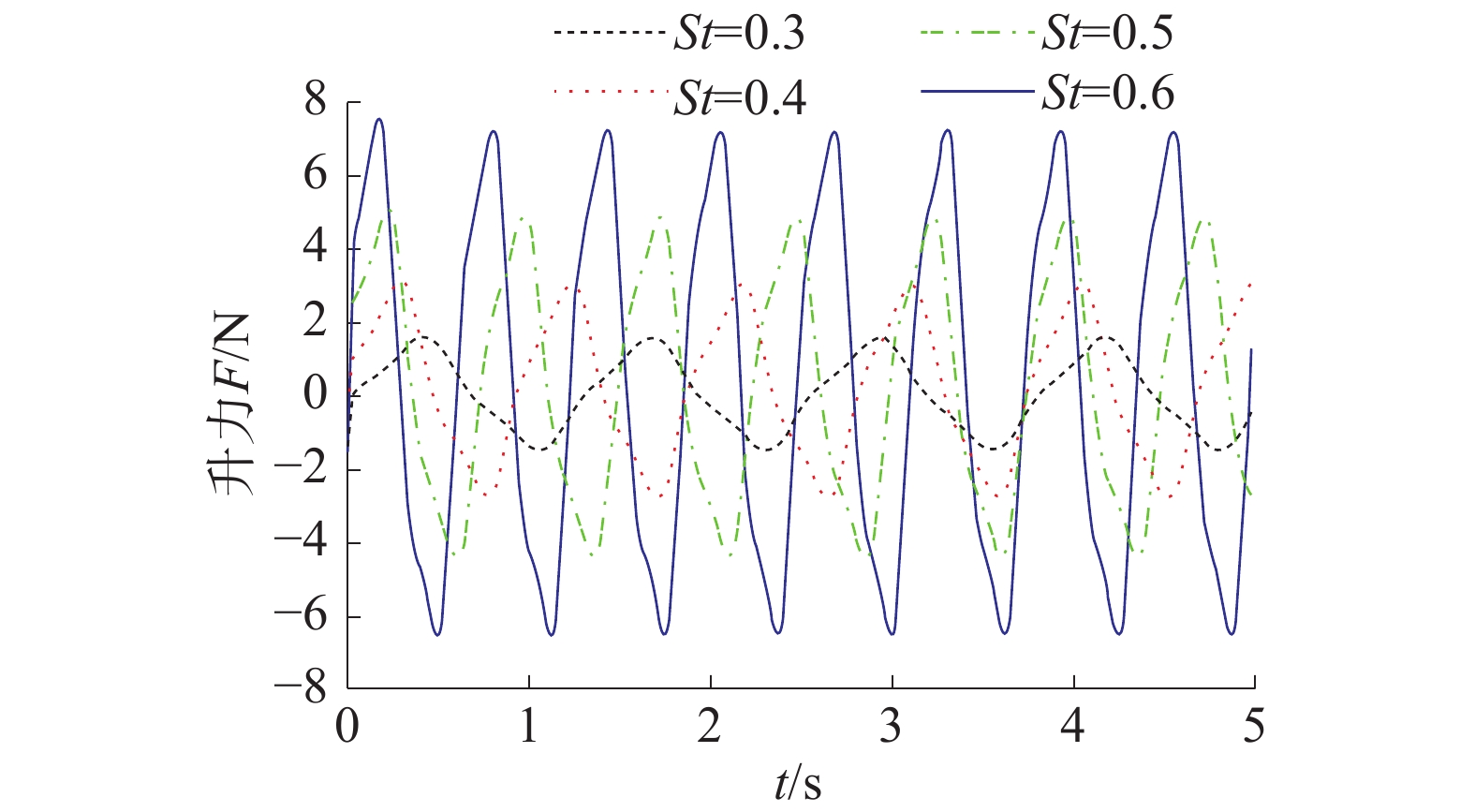
从图7可以看出,升力曲线为周期性分布,与本文设置的摆动翼周期性运动有关,并且大致关于直线y=0上下对称。与推力曲线相同,随着St数的增加,周期减小,相同时间段内的周期数增加,曲线变得更加密集,但升力曲线的周期是推力曲线的2倍。
|
Download:
|
| 图 7 摆动水翼所受升力曲线 | |
从图8可以看出,力矩曲线与升力曲线相同,也为周期性分布,并且周期相同,随着St数的增加,周期减小,力矩曲线变得更加密集。力矩曲线大致关于直线y=0上下对称。

|
Download:
|
| 图 8 摆动水翼所受力矩曲线 | |
图9中的环形区域即是摆动翼运动所产生的尾涡,尾涡记录了流体域中的速度和压力所产生的变化,在摆动翼周围尾涡较小,中心区压力较大,尾涡的压力梯度也很大;远离摆动翼的尾涡变大,中心压力值减小,压力梯度也减小,在无穷远的区域中尾涡已经消失。并且尾涡呈交错排列,连接在一起呈正弦三角函数分布,在波峰波谷处出现尾涡,尾涡的数量随着St的增大而增加,这说明尾涡与摆动翼的运动频率有关。

|
Download:
|
| 图 9 尾涡图 | |
以上现象与尾涡的产生机理密切相关,本文中摆动翼在y向做升沉和俯仰运动时,初始位置为摆动翼运行的最高位置,之后摆动翼将向下运动,此时翼型下部形成高压区域。第一次经过平衡位置处,翼型与x轴正向夹角为负,当摆动翼到达最低位置时开始向上运动,此时翼型上部形成高压区域;第二次经过平衡位置时,翼型与x轴正向夹角为正,之后再一次到达最高位置,以后循环以上运动,摆动翼做俯仰运动的旋转轴在距摆动翼头部0.3倍弦长处。
翼型下降过程中,下部形成高压中心,随着翼型俯仰角度的变化,高压中心逐渐移动到翼型尾部,在最低位置处脱落;同样,翼型上升过程中,上部形成高压中心,随着翼型俯仰角度的变化,高压中心逐渐移动到翼型尾部,在最高位置处脱落。因此可以观察到波峰和波谷处出现速度中心和压力中心,同时,随着St数的增大,周期缩短,出现了更多的速度中心和压力中心。
4 结论本文采用重叠网格方法,分析了仿生摆动水翼的水动力特性,得到了与预期结果和实际现象相符合的结果,并根据实际现象对计算所得的结果进行了合理的解释。
1)摆动水翼上方和下方交替出现高压区域,摆动水翼上下的压力差产生推水的效果;
2)当平移幅值、水流进速和俯仰角度幅值都固定不变时,水动力性能随St数的变化而变化,最大推力、最大升力和最大力矩都随着St数的增大而增加;
3)推力、升力和力矩曲线都呈现周期性规律,这与摆动翼的运动规律有关,摆动翼的运动模型是用三角函数表示的运动,由此导致了尾涡在波峰和波谷出现,尾涡的反卡门涡街式的排列使得摆动水翼产生了推力。
本文模拟分析了流场中仿生摆动水翼表面的压力分布,对摆动水翼所受的推力、升力和力矩进行监控,并同时监控摆动翼在模拟水池中压力标量场以及翼型运动时的尾涡情况,详细分析了翼型的水动力性能随St数的变化的影响,得到了具有普遍意义的规律。
| [1] |
胡波. 中国的深海战略与海洋强国建设[J]. 人民论坛•学术前沿, 2017(18): 12-21. ( 0) 0)
|
| [2] |
杨亮. 仿金枪鱼摆动尾鳍的水动力性能与推进机理研究[D]. 哈尔滨: 哈尔滨工程大学, 2009.
( 0) 0)
|
| [3] |
张曦. 仿鱼类摆动尾鳍推进系统的水动力研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
( 0) 0)
|
| [4] |
LIGHTHILL M J. Large-amplitude elongated-body theory of fish locomotion[J]. Proceedings of the royal society of London. Series B. Biological sciences, 1971, 179(1055): 125-138. DOI:10.1098/rspb.1971.0085 ( 0) 0)
|
| [5] |
CHOPRA M G, KAMBE T. Hydromechanics of lunate-tail swimming propulsion[J]. Journal of fluid mechanics, 1977, 79(1): 46-69. ( 0) 0)
|
| [6] |
WU T Y T. Swimming of a waving plate[J]. Journal of fluid mechanics, 1961, 10(3): 321-344. DOI:10.1017/S0022112061000949 ( 0) 0)
|
| [7] |
程健宇, 庄礼贤, 童秉纲. 三维变幅波板的游动[J]. 水动力学研究与进展, 1991, 6(增刊1): 1-11. ( 0) 0)
|
| [8] |
CHOPRA M G. Large amplitude lunate-tail theory of fish locomotion[J]. Journal of fluid mechanics, 1976, 74(1): 161-182. DOI:10.1017/S0022112076001742 ( 0) 0)
|
| [9] |
苏玉民, 黄胜, 庞永杰, 等. 仿鱼尾潜器推进系统的水动力分析[J]. 海洋工程, 2002, 20(2): 54-59. DOI:10.3969/j.issn.1005-9865.2002.02.010 ( 0) 0)
|
| [10] |
梁建宏, 郑卫丰, 文力, 等. 两关节仿生水下航行器SPC-Ⅲ的推进与机动性[J]. 机器人, 2010, 32(6): 726-731, 740. ( 0) 0)
|
| [11] |
ZHU Q, WOLFGANG M J, YUE D K P, et al. Three-dimensional flow structures and vorticity control in fish-like swimming[J]. Journal of fluid mechanics, 2002, 468: 1-28. ( 0) 0)
|
| [12] |
GOPALKRISHNAN R, TRIANTAFYLLOU M S, TRIANTAFYLLOU G S, et al. Active vorticity control in a shear flow using a flapping foil[J]. Journal of fluid mechanics, 1994, 274: 1-21. DOI:10.1017/S0022112094002016 ( 0) 0)
|
| [13] |
吴峰. 湍流的本质及湍流方程的封闭[J]. 中国科学技术大学学报, 2002, 32(6): 754-756. DOI:10.3969/j.issn.0253-2778.2002.06.021 ( 0) 0)
|
| [14] |
MENTER F R. Zonal two equation k-ω turbulence models for aerodynamic flows[C]//Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference. Orlando, USA, 1993.
( 0) 0)
|
| [15] |
LU Kun, XIE Yonghui, ZHANG Di. Nonsinusoidal motion effects on energy extraction performance of a flapping foil[J]. Renewable energy, 2014, 64: 283-293. DOI:10.1016/j.renene.2013.11.053 ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


