2. 哈尔滨工程大学 核安全与仿真技术国防重点学科实验室,黑龙江 哈尔滨 150000
2. Fundamental Science on Nuclear Safety and Simulation Technology Laboratory, Harbin Engineering University, Harbin 150001, China
鼓泡塔能够提供较大的气液接触面积和接触时间,其在化工、冶炼、生物制药等领域得到广泛应用。气液间的传质面积是影响鼓泡过滤性能的主要参数。在相同的气体流量下,球形气泡尺寸越小,气液界面面积浓度越大,相间传质面积也相应增大。此外,气泡在上升过程中因受到惯性力、浮力和剪切力等作用会发生变形[1−3]。气泡体积相同时,变形程度越大,气液间的接触面积也就越大。因此,在鼓泡塔中实际的气液间传质面积应由气泡体积和气泡变形情况共同决定。Aybers等[4]研究结果表明,当气泡直径较小时,由于表面张力的作用,气泡呈球形;随着气泡直径的增大,气泡形状依次经过球形、椭球形、表面波动状态和圆帽形。在气泡上升过程中,其形状始终发生变化,因此采用合适的方法确定气泡体积和界面面积,并建立时间尺度上的均值,对于鼓泡塔的设计和性能评价至关重要。
目前,已有很多测量气泡特性的方法,主要分为接触式和非接触式2种。接触式的测量方法主要有光纤探针法、电导法、取样探针法、相敏恒温测速法以及wire-mesh传感器[5−8]。相比于接触式测量手段,非接触式方法具有不干扰流场和高空间分辨率的优点,非接触式测量手段包括X射线技术、激光多普勒干涉测速法和图像处理法等多种测量手段[9−10]。近年来,随着高速摄影技术的发展,图像处理技术越来越受到重视[11−12]。Lecuona[13]提出针对高含气率条件,使用分水岭法分割气泡的图像处理技术。在计算气泡体积的问题上,由于多数学者所研究的气泡直径小于4 mm,气泡变形程度不大,气泡体积通常采用等效直径法和椭球体积计算公式得到[14−15]。然而在安全壳过滤排放系统的鼓泡装置中,生成气泡体积较大,气泡变形情况严重。此时,使用传统的图像处理技术获得的气泡尺寸与气泡实际尺寸相差较大,无法真实地反应出气泡的体积和界面面积。因此,本文以大尺寸不规则气泡为研究对象,采用实验方法验证并评价了现有图像处理技术的优缺点,并提出一种改进的图像处理技术来计算气泡体积。
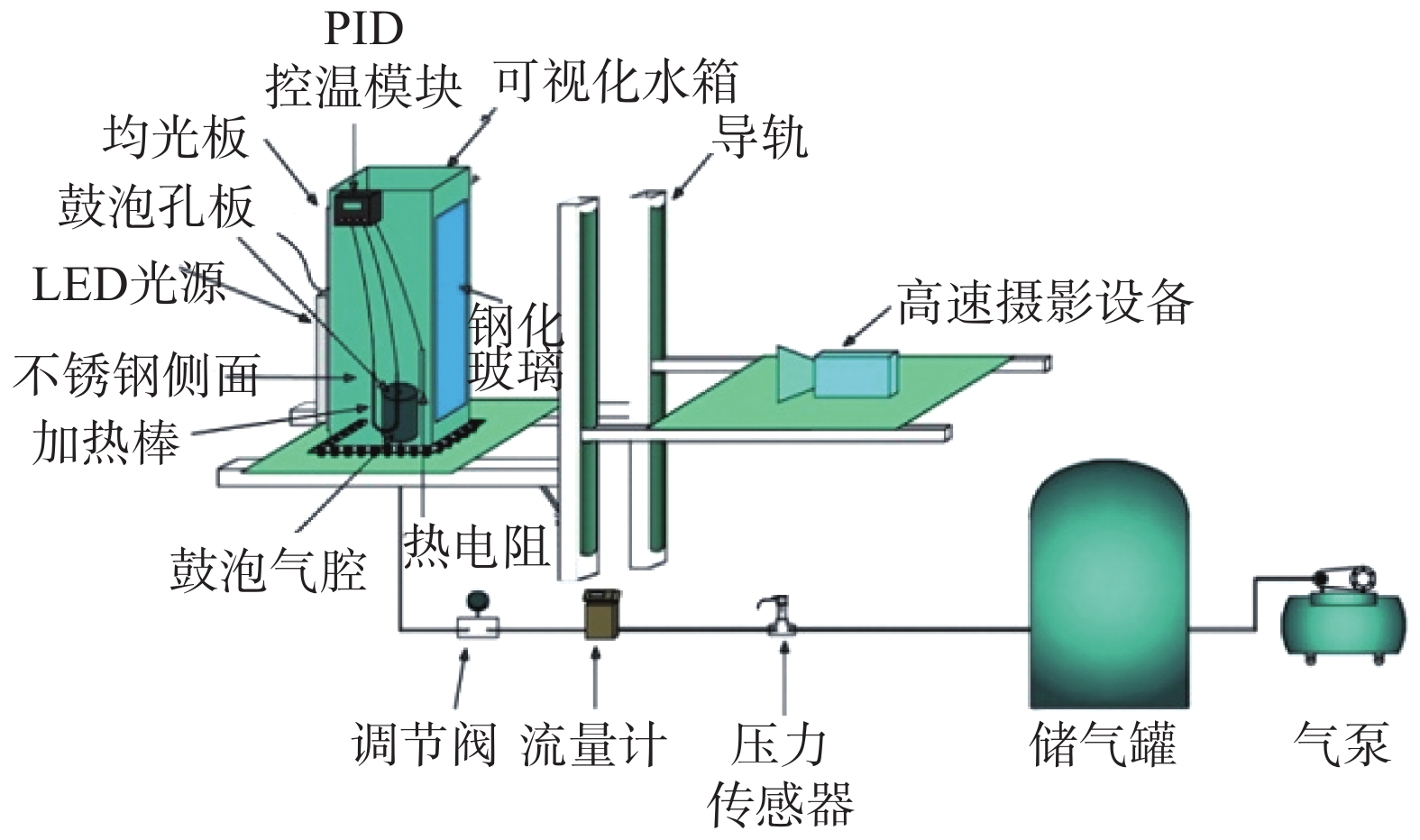
1 实验装置与误差分析 1.1 实验装置研究中所用实验装置如图1所示,该装置可以分别采用图像处理和气泡采样2种方法来测量气泡的体积。实验装置主体为可视化水箱,水箱横截面长宽分别为200 mm和170 mm,该尺寸足以避免箱体壁面对气泡的影响,使其处于自由上升状态。可视化水箱的前、后两面采用钢化玻璃,两侧面采用不锈钢作为钢化玻璃的支撑。一个功率为12 W的LED光板紧贴在可视化水箱后侧作为冷光源使用。LED光板具有无频闪的优点,适用于高速摄影的拍摄条件。在LED光源和钢化玻璃之间安装有均光板,起到调控光强并均化光强分布的作用。在可视化水箱的前面放置一台高速摄影设备,为方便调整焦距并实现能够拍摄不同高度的功能,高速摄影设备放置的平台含有2套导轨系统,保证高速摄影设备可以沿竖直方向和垂直可视化面的方向移动。进行可视化实验的高速摄影设备为PHANPOM V641,拍摄速率为1 000 f/s,分辨率为0.05 mm/pix。该实验装置使用PID技术实现温度调控,测温元件为PT-100热电阻,加热单元为1 kW加热棒,控温系统控温误差在1 ℃之内。鼓泡实验中以压缩空气和去离子水为工质。压缩空气通过气泵提供,并经体积为1 m3的储气罐来稳定压力,以保证供气的流量恒定。供气流量采用调节阀来改变,并利用Aalborg公司的质量流量计来记录。气泡鼓泡时间间隔为0.2~0.25 s,孔板直径为2 mm,气腔直径为100 mm,高80 mm。通过在气泡位置放置直尺在图像中建立比例尺。此外,为了将图像处理得到的气泡体积与实际气泡体积进行对比,采用气泡收集法对气泡平均体积进行测量。气泡个数对分析结果有一定的影响[16],不同的研究人员选择了不同的气泡收集数量,如50~100个[17]、200个[18]、250个[19]、300个[20]以及250~300个[21]。本文为保证取样气泡的代表性,将收集气泡数量定为100~300个。气泡收集法的具体方法为:将量筒装满水,倒置在实验液体中,量筒的位置能够保证产生的气泡进入到量筒之中,气泡进入量筒后将量筒中的液体排出。计入量筒的气泡数量通过人工统计,气泡总的体积可通过量筒的刻度线得到。
|
Download:
|
| 图 1 实验装置简图 | |
由于生成气泡的气体流速较低,气泡生长过程处于表面张力控制区,生成的气泡体积由公式(1)决定。
| ${\text{π}} {{{d}}_{{h}}}\sigma = \frac{1}{6}{\text{π}} {d_b}^3{\rho _l}g$ | (1) |
式中:dh为鼓泡口孔径,mm;
液相温度变化会造成表面张力改变进而影响生成气泡的体积,实验中温度控制设定在25 ℃,考虑到热惯性作用和控温装置自身的影响,温度波动范围在23~27 ℃。此时表面张力变化范围为71.69~72.6 mN/m,由式(1)计算得到气泡体积会有±0.42%的波动。收集气泡法测量气泡体积过程中使用分度值为1 mL的量筒收集气泡,因此,所收集气泡的总体积的读数误差为±1 mL。气泡数量为人工计数,保守估计存在±5的读数误差,当收集气泡数量为100时,气泡计数的相对误差最大,为±5%。图像处理计算气泡体积的误差主要来自分辨率和比例尺标定。在处理气泡图像过程中,由于拍摄图像分辨率的限制,在气泡边界两侧各存在一个像素点的识别误差。当气泡直径为5 mm时,该误差会造成气泡体积计算误差为6%;当气泡体积为10 mm时,该误差为3%。在标定过程中,标定直尺无法与拍摄镜头保持绝对平行,因此标尺读数与实际长度存在误差。标定直尺长度为50 mm,误差不超过1 mm,当气泡体积为5 mm时,该误差造成气泡体积误差为12%。
2 图像处理技术图像处理技术包含预处理和计算2个环节。通过高速摄影技术得到气泡上升过程图像后,需对原始图像进行预处理以得到清晰的气泡边界轮廓。根据图像处理方法的不同,对气泡轮廓按相应方法进行处理,进而计算得到气泡体积。
2.1 图像预处理在实际的拍摄时,由于气腔和孔板不可避免地会有一部分进入到拍摄画面中,需要将拍摄的含有气泡的画面减去拍摄背景,以消除其他物体的干扰。此外,如图2(a)所示,拍摄光源强度分布不均、可视化面加工不平整以及存在划痕会使拍摄图像中产生干扰项。因此,在利用图像法处理气泡体积之前,需要对图像进行预处理以便提高图像质量。预处理时首先利用差影法将拍摄气泡图像与背景图像相减,以消除图像中的无关物体的影响。处理后图像如图2(b)所示,在得到去除背景的图像后,应用中值滤波法将图像中小噪声干扰进行去除。为了进一步提高图像质量,对图像进行二值化,如图2(c),并填充气泡区域,如图2(d)。由于计算气泡体积等参量所需的关键信息在气泡投影的边界处获取,因此将处理得到的气泡图像进行边界提取以便进行后续的计算,处理后所得的气泡轮廓如图2(e)所示。

|
Download:
|
| 图 2 图像预处理效果 | |
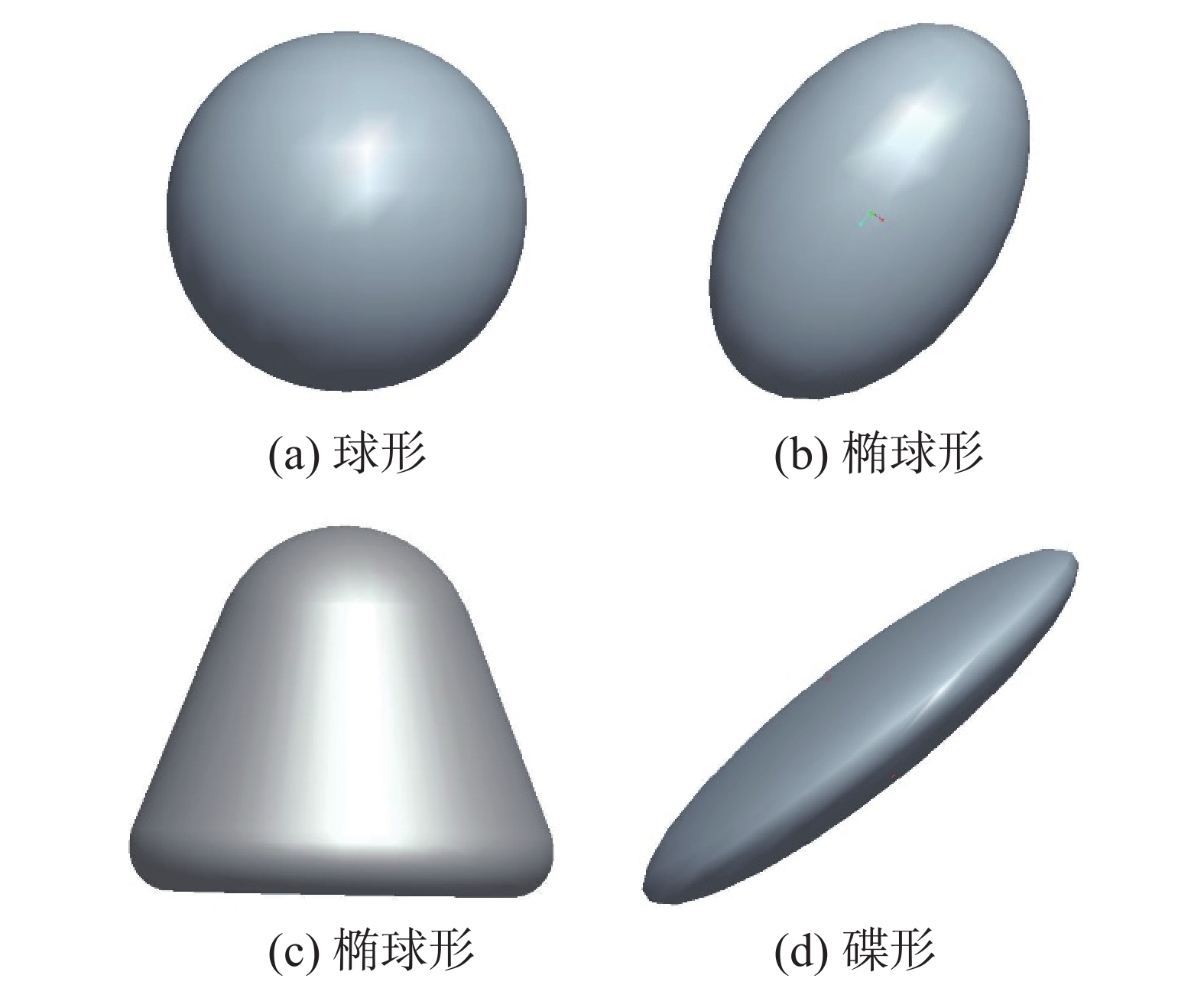
为了避免气溶胶堵塞孔口,安全壳过滤排放系统中所用孔板的孔口直径一般在1 mm以上,因而生成的气泡直径都大于5 mm。大尺寸气泡在上升过程中会发生明显的变形,呈现出不同的几何形态,如圆帽形、子弹形、椭球形等。如图3所示,在图像处理过程中,根据变形气泡的形状不同,将气泡大体分为3类:圆帽形、椭球形和碟形。其中球形可以作为椭球形的一种特例。
|
Download:
|
| 图 3 典型气泡形状 | |
由于目前所研究的气泡体积计算方法多针对直径较小的气泡,在获得图2(e)中的气泡投影轮廓后,已有计算气泡体积的方法主要有等效直径法和椭球体积计算公式2种。等效直径法(equivalent diameter method,EDM)的基本思想是认为气泡形状为球形或近球形,在拍摄照片中,球形气泡的投影呈圆形。由于球形具有完美的中心对称的特点,球形气泡在任意方向上投影的圆形大小均不变,而且圆形直径与球形直径相等。通过计算投影圆形的面积可以得到圆形直径,进而计算出球形气泡的体积,如式(2)所示:
| $V = \displaystyle\frac{4}{3}{{\rm{\text{π} }}^{ - \textstyle\frac{1}{2}}}{ A ^{\textstyle\frac{3}{2}}}$ | (2) |
式中:V为气泡体积,mm3;A为气泡投影面积,mm2。
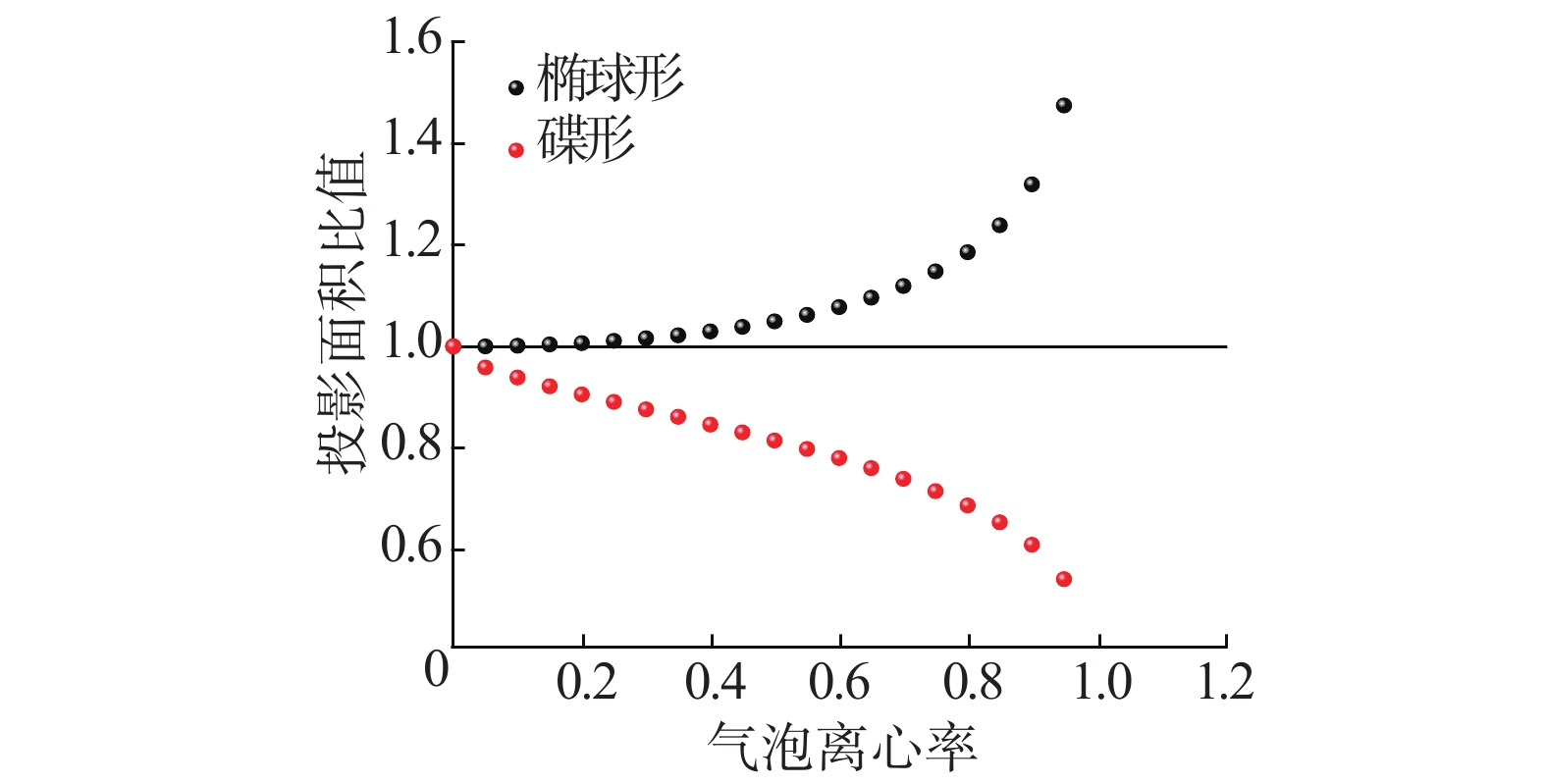
等效直径法就是将不同形态的气泡投影等效成与投影面积相等的圆,然后利用该等效圆的直径来计算气泡的体积。由此可知,当气泡为规则球形时,采用等效直径法计算出来的气泡体积是准确的。然而,气泡的投影面积受气泡的几何形状以及气泡的变形程度影响较大。当气泡存在变形时,利用平面上的投影面积计算的等效直径来计算气泡体积将会出现偏差。图4中给出了不同变形程度的椭球体与碟形体在平面上的投影面积与等体积的球体在平面上的投影圆面积的比值。由图4可以看出,对于气泡形状为图3(b)所示的椭球体而言,当变形程度较小时,在平面上的投影面积近似与投影圆面积相等,表明此时利用该面积计算出的等效直径来求椭球体积是接近的。然而,随着投影面积离心率的增加,椭球体投影面积与等体积球体投影圆面积的比值逐渐增加,表明此时再用投影面积的等效直径来计算椭球体积将明显大于实际体积,存在较大的计算偏差。当气泡形状为图3(d)所示的碟形时,投影面积与等体积球体投影圆面积的比值随离心率的增大而减小。因此,采用等效直径法也很难准确计算出气泡的真实体积。如图5所示,此时计算得到与投影面积相等的圆形的直径不能很好表征气泡体积大小,该直径与同气泡体积等效直径存在较大出入。随着气泡变形程度的增加,2种直径相差越大。所以采用等效直径法计算的体积与真实体积的偏差也随着气泡变形程度的增加而增大。
|
Download:
|
| 图 4 相同体积气泡下气泡投影面积同离心率和气泡形状种类的关系 | |

|
Download:
|
| 图 5 相同体积气泡下气泡体积比同离心率和气泡形状种类的关系 | |
利用椭球体积计算公式(ellipsoid volume calculation formulation,EVCF)计算气泡体积的基本思想是将气泡看作椭球体,利用式(3)进行计算。
| $V = \frac{4}{3}{\text{π}} {a^2}b$ | (3) |
式中:V为气泡体积,mm3;a为气泡长轴,mm;b为气泡短轴,mm。
因为从二维图像上无法获取椭球3个旋转轴的信息,使用该方法时,通常认为水平穿过气泡的直线被气泡边界截得的最长弦为气泡长轴,过长轴中点且垂直于长轴的直线被气泡边界截得的弦为气泡短轴。在气泡为椭球体的假设下,认为图像无法体现的第3个方向上的轴长与图像中气泡的长轴相等。图5中可以看到,利用该方法对碟形气泡的体积计算较为准确。而对于椭球形气泡而言,当气泡的离心率较小时,利用椭球体积计算公式计算的结果与实际符合较好;而随着气泡的离心率增大,利用该方法计算的结果比实际体积值明显偏大。因为此时第三方向上气泡的轴长与图像中的短轴相等,而椭球体积公式中将其假设为与长轴相等,显然是不合理的。而对于圆帽形气泡而言,由于气泡无明显的长轴和短轴,因此为椭球计算公式法的使用带来了困难。需要说明的是,图5中使用椭球体积公式法时未考虑气泡对称轴发生偏转的情况。当气泡对称轴发生偏转后,椭球体积计算公式法的计算精度会进一步下降。
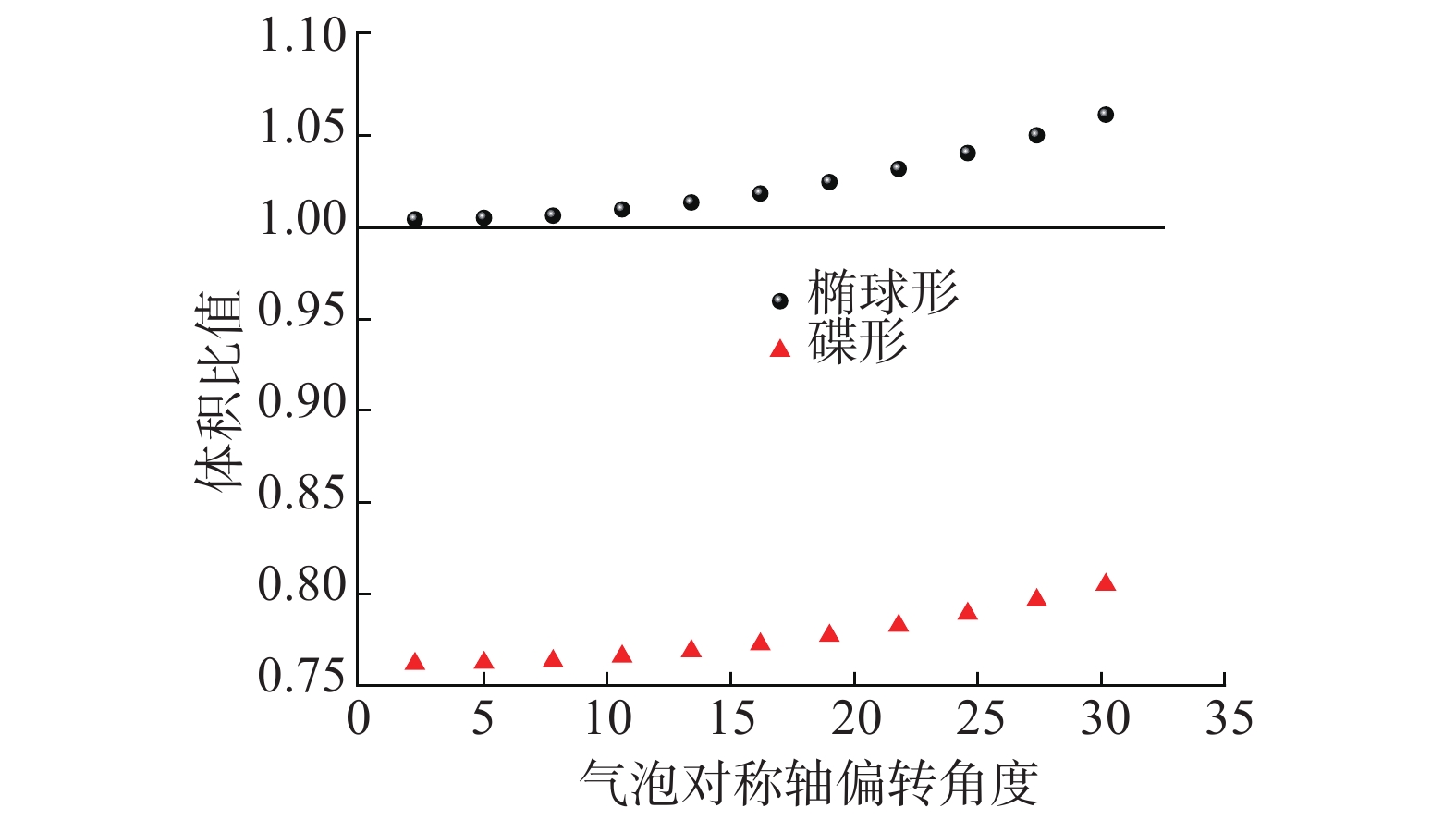
2.3 水平切片法在气泡上升过程中,虽然气泡存在较大变形,但仍具有轴对称特性。利用气泡具有轴对称性的特点,可以采用切片法提高图像处理技术计算气泡体积的精度。切片法的基本思想是将图像中气泡投影按一定方式切割成多份薄片,每份薄片按圆柱体处理来计算其体积,然后将各薄片体积求和。该方法具有更高的灵活度,并不受气泡形状的约束。目前已有一部分学者使用水平切片法来处理气泡体积。但是在气泡上升过程中,其对称轴不会始终处于竖直状态,而会发生一定的偏转。针对对称轴发生偏转的状态,水平切片法的计算精度会下降。而且,对于不同形状的气泡,单纯采用水平的切片方向也会造成较大的偏差。如图6所示,当气泡为椭球体时,随着气泡对称轴偏转角增加,水平切片法的计算精度变得越来越差。当偏转角度大于27.5°时,水平切片法的计算误差大于5%。当气泡为碟形时,水平切片法的计算结果明显小于实际体积。造成水平切片法处理结果变差的原因是该方法只能单纯地水平切割气泡图像,不能识别气泡几何特征并选择合适的切片方向。因此,当气泡为如图3(d)所示的碟形时,利用水平切割产生的小圆柱体不能充分地贴合气泡表面,而是比实际的气泡表面要小得多,因此计算出来的小圆柱体的体积之和无法准确反映出真实的气泡体积。从图6中可以看出,对于图3(d)所示的碟形气泡,水平切片法计算的气泡体积明显小于实际的气泡体积。因此需要根据对称轴的方向和气泡形状来选择切片方法,基于这种方法中存在的不足,提出了下面的自适应切片法。
|
Download:
|
| 图 6 气泡偏转角和形状对水平法计算结果影响 | |
自适应切片方法改进了水平切片法的缺陷,其能够判别气泡所属的形状种类,并选定合适的切片方向。使用自适应切片法的关键是能够准确地找到气泡的对称轴,并以气泡的对称轴为参考,结合气泡的变形度来自动选择气泡的切片方向,使得切片后所得的圆柱体更贴合气泡表面,从而提高气泡体积的计算精度。在自适应切片法中,为方便找出气泡对称轴,本文引入能够定量计算几何对称性的量Ia。
| ${I_a} = {\sum\nolimits_{k = 1}^m {\left( {{L_1} + \varphi {L_2}} \right)} ^2}$ | (4) |
式中:
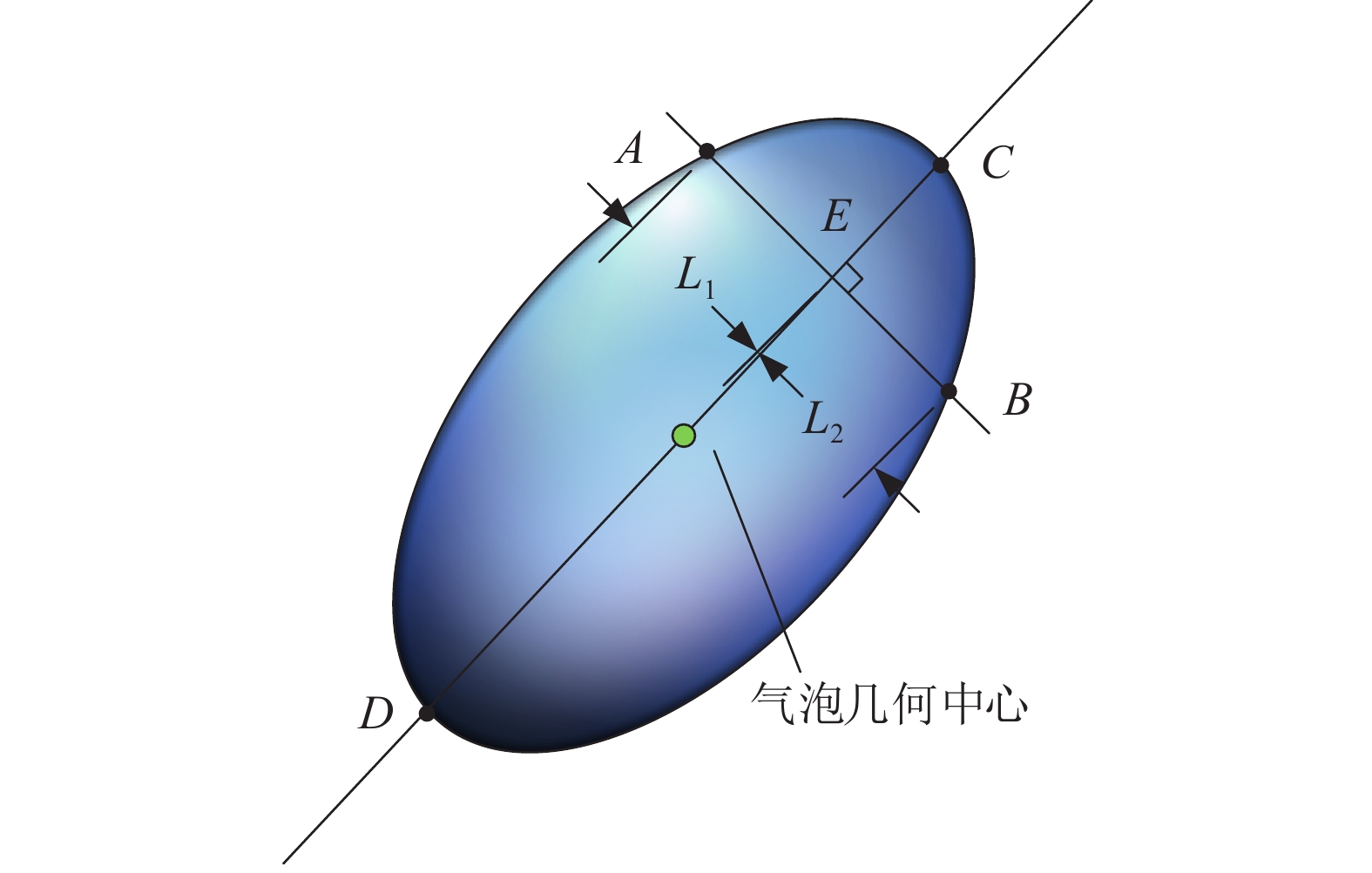
如图7所示,为了计算一个几何体相对于某一条直线的对称性,做垂直于该直线的数条垂线,求各垂线与几何轮廓交点到该直线距离差值,然后对每条垂线形成的距离差值进行平方相加,从而得到定量的对称性。若几何体相对于该直线对称性越好,则对称量Ia值越小;当直线为几何体的对称轴时,对称量Ia的值为零。为了避免气泡不规则凹凸对寻找对称轴的影响,首先确定气泡的几何中心。过气泡几何中心做直线扫描气泡所在平面,找出使气泡轮廓对称量最小的直线作为气泡的对称轴线,记为第一对称轴。过气泡轮廓的几何中心做垂直第一对称轴的直线,记为第二对称轴。为了增强切片法的灵敏度,选择两对称轴中较长的轴作为切片法的参考轴。由于气泡的变形导致气泡上升过程中形状时刻发生变化,如2.3节中所述,对应不同的气泡形状采用相同的切片方向势必造成气泡体积的计算偏差。因此,为了提高计算精度,自适应切片法可根据气泡的形状来确定切片方向。当气泡为碟形时,采用平行于长对称轴方向切割气泡轮廓;而当气泡为椭球体或圆帽形时,采用垂直于长对称轴的方向切割气泡。因此,这一方法的关键是能够准确地判断气泡形状。如图8所示,气泡的形状与气泡的变形程度有关系,因此本文使用如式(5)所示的圆形度概念来表征气泡变形程度,进而建立气泡形状和圆形度的关系
| $C = \frac{{4{\rm{{\text{π}} }}A}}{{{P_b}^2}}$ | (5) |
|
Download:
|
| 图 7 计算对称性示意图 | |

|
Download:
|
| 图 8 不同圆形度下切片方向对气泡体积计算结果的影响 | |
式中
图8为不同圆性度下切片方向对气泡体积计算结果的影响。从图8中可以看出,虽然液相温度、液相成分和浓度发生变化会改变液相物理性质,但当气泡圆形度小于0.6时,平行于气泡长对称轴切割气泡的计算结果精度要明显优于垂直于长对称轴方向切割的计算精度;反之,当图像中气泡的圆形度大于0.6时,垂直于气泡长轴切割方式的计算精度更高。这表明,当气泡的圆形度小于0.6时,气泡的几何形状为圆盘状;当气泡的圆形度大于0.6时,气泡的几何形状为圆帽形或椭球形。因此可以根据气泡的圆形度选定合适的切片方向,这也使得自适应切片法对气泡形状的适应性更强,从而比水平切片法具有更高的计算精度。
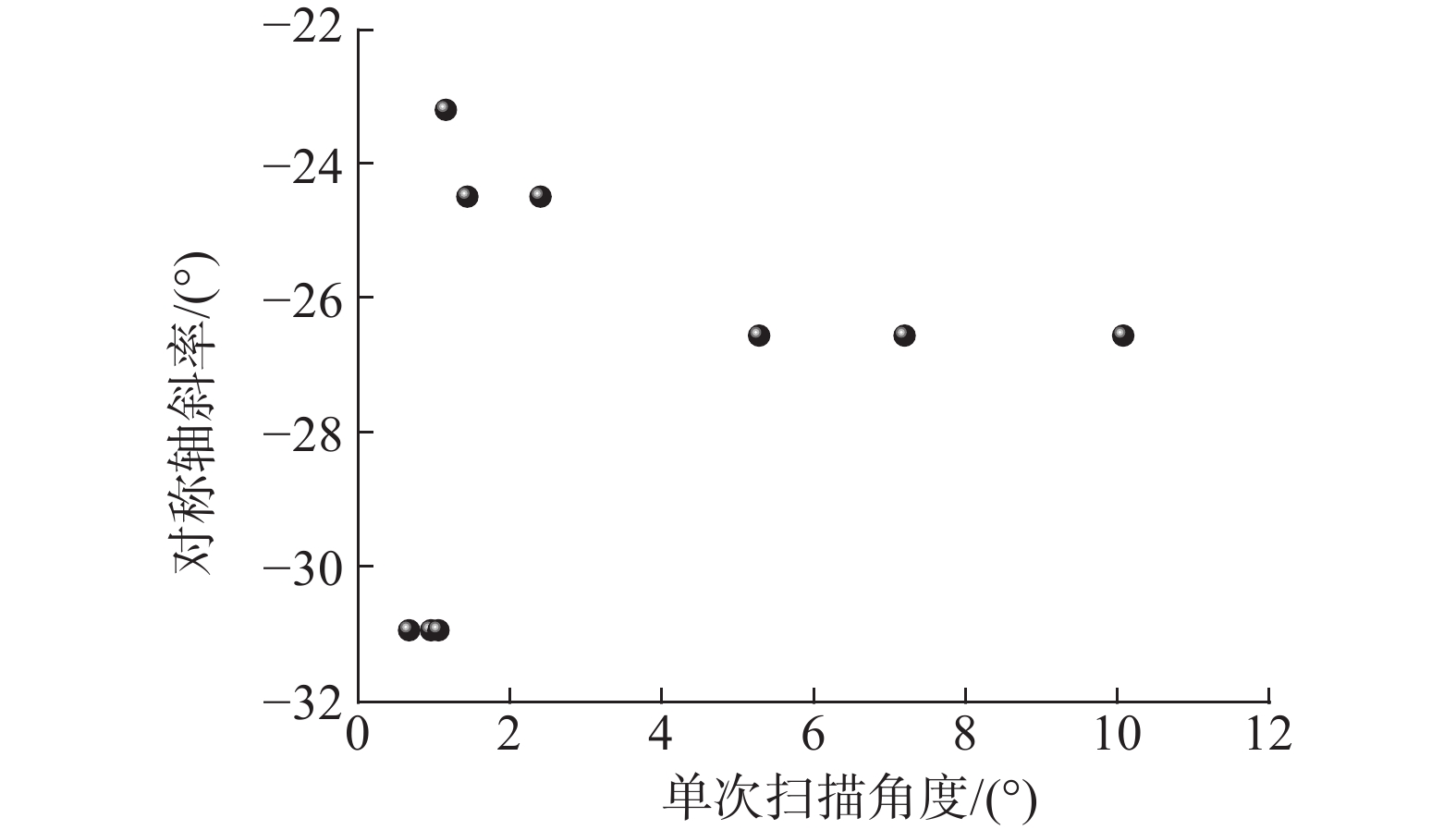
3 不同图像处理方法的实验验证由于切片法是对气泡轮廓进行切割,此外在自适应切片法中,还要过气泡轮廓中心扫描寻找对称轴,因此,分割气泡轮廓的份数和每次扫描转过的角度决定了切片法的计算精度。在使用切片法之前,需要对切片份数和单次扫描角度进行无关化验证。如图9所示,当切片份数大于500后,计算得到的气泡体积结果趋于稳定,不再随切片份数的增加而明显的变化。如图10所示,使用自适应法时,当单次扫描角度达到0.5°时,计算得到的气泡体积结果基本稳定。为了保证计算精度并尽量减少计算量,本文在使用切片法时,切片份数选为500;使用自适应切片法时,单次扫描旋转角设为0.5°。

|
Download:
|
| 图 9 计算得到的气泡体积同切片数量关系 | |
|
Download:
|
| 图 10 计算得到的气泡对称轴斜率同单次扫描角度关系 | |
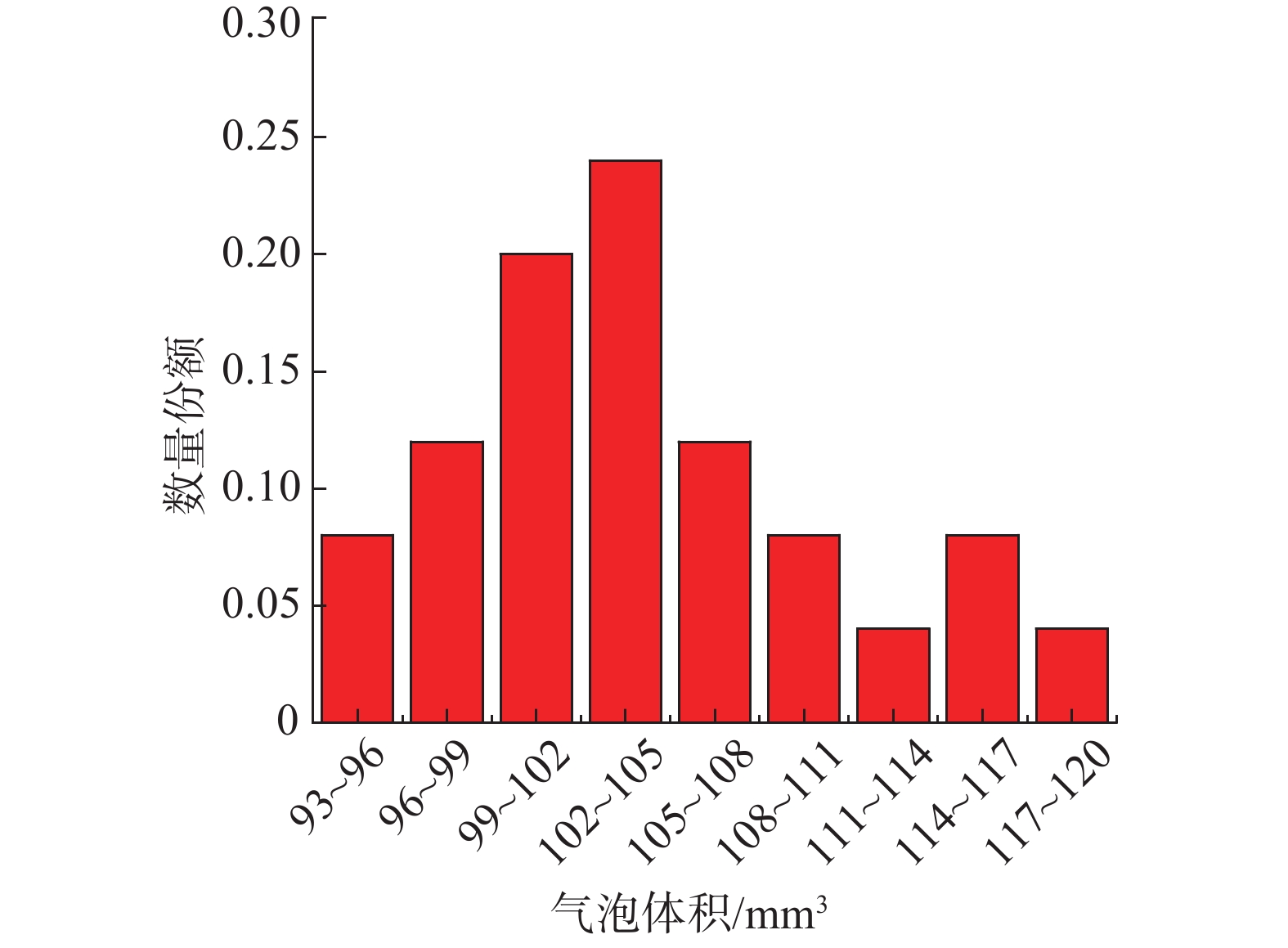
为了验证图像处理方法计算的准确性,利用气泡收集法(bubble collection method,BCM)获取到气泡的实际平均体积。由于收集法仅能获得气泡的平均体积,若各气泡间尺寸差异较大,则平均气泡体积无法用来标定或验证图像法处理的单个气泡体积的结果。因此,本工作中尽量维持气泡生成的条件固定。此外,对气泡尺寸分布进行了测量。测量方法为使用量筒收集单个气泡,然后使用微型注射器将量筒内的气体抽尽,微型注射器的最小刻度为3 mL。得到不同的尺寸范围下的气泡数量份额如图11所示。虽然气泡尺寸不是单一的,但分布范围较窄,气泡尺寸的离散程度要小于1.2节中分析的图像误差。因此,可以用收集法得到的实验结果作为图像法的验证标准。
|
Download:
|
| 图 11 收集法得到的气泡尺寸分布 | |
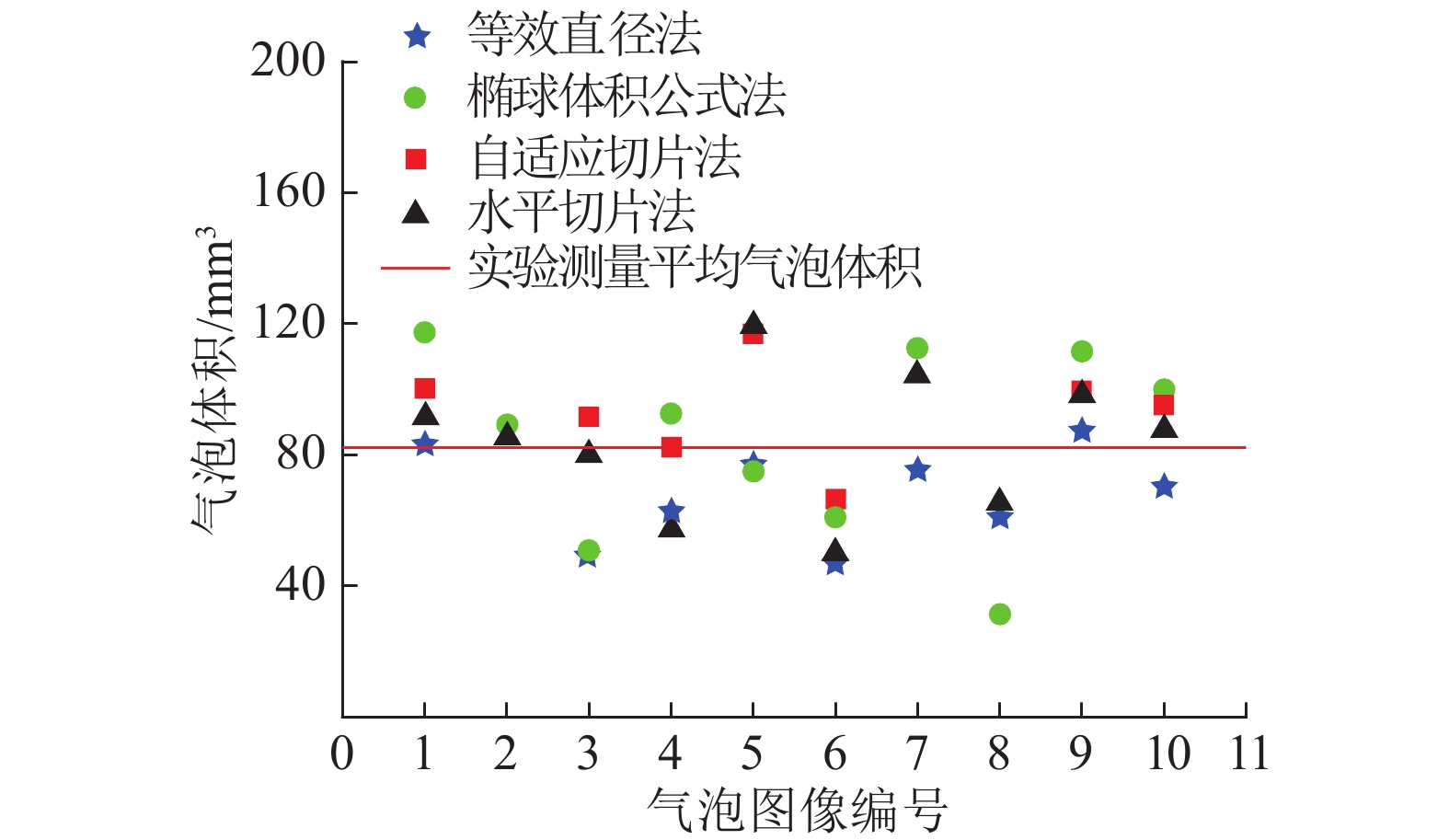
根据前文回顾文献中气泡收集法所收集的气泡个数,本研究中分别收集了100个和300个气泡,得到气泡总体积分别为10.5 mL和31.5 mL。计算气泡的平均体积为105 mm3。由于气泡收集过程是在液相表面完成,因而在淹没30 cm状态下拍摄气泡。利用理想气体状态方程对气泡体积进行换算得到拍摄位置气泡体积应为102 mm3。图12给出了随机选取的10个具有不同形状、不同变形程度的气泡图像,将其编号为(1)至(10)。采用不同图像处理技术来计算这些气泡的体积,并与实验测量值进行分析比较。表1中给出了不同图像处理方法的性能对比,图13中给出了具有代表性的10种气泡形态在4种不同图像处理方法下计算的气泡体积结果。结果表明使用等效直径法得到气泡体积是4种图像处理方法所得结果中最小的。对于形状偏离圆形较大的气泡,如图12编号(2)~(7)所示的气泡,采用等效直径法的计算精度明显变低,此时该方法已不再适用。如图12编号(8)中,气泡形状发生较大变化时,气泡的长轴和短轴有大幅度改变,从而造成椭球体积公式的计算结果出现很大变化。因此,椭球体积计算公式的计算结果方差是4种图像处理方法中最大的。当气泡形状如图12编号(4)所示,气泡对称轴偏转角较大的情况不适合使用水平切片法处理气泡体积。总体来讲,自适应切片法在面对不同气泡形态时表现出更准确的计算精度,并且自适应切片法计算结果方差最小。

|
Download:
|
| 图 12 不同编号的气泡图像 | |
|
|
表 1 对应不同方法的气泡平均体积与方差 |
|
Download:
|
| 图 13 4种图像处理方法针对不同形状气泡计算结果比较 | |
当气泡体积较大时,气泡会发生明显的变形,为利用图像法计算气泡体积带来了难度。本文介绍了4种利用图像技术处理气泡体积的方法,并通过气泡收集法作为实验手段,测量得到气泡平均体积,将4种图像处理方法得到的计算结果与实验结果进行比对,得到如下结论:
1)当气泡变形较大从而造成气泡形状偏离球形时,气泡在图像上的投影面积会发生改变,使用等效直径法得到的气泡等效直径会发生变化,进而造成等效直径法计算精度的下降。
2)传统的椭球体积计算法因分别选取图像中气泡的水平轴和竖直轴作为长轴和短轴而无法考虑到气泡形状类型发生变化,因此该方法计算结果存在很大的离散性。
3)在气泡上升过程中,其旋转轴发生偏转以及气泡形状的差异,均造成水平切片法的计算精度下降。对椭球型气泡,偏转角度大于27.5°时,误差超过5%;对碟形气泡,误差高达20%以上。
4)在能够准确判断气泡几何形状的基础上,自适应切片法可以根据图像中气泡的对称轴和气泡形状选定合适的切片方向进行图像处理。对于高变形的气泡,自适应切片法具有良好的计算精度和稳健性。
| [1] |
LEGENDRE D, ZENIT R, VELEZ-CORDERO J R. On the deformation of gas bubbles in liquids[J]. Physics of fluids, 2012, 24(4): 043303. DOI:10.1063/1.4705527 ( 0) 0)
|
| [2] |
KYRIAKIDES N K, KASTRINAKIS E G, NYCHAS S G, et al. Bubbling from nozzles submerged in water: transitions between bubbling regimes[J]. The Canadian journal of chemical engineering, 1997, 75(4): 684-691. DOI:10.1002/cjce.v75:4 ( 0) 0)
|
| [3] |
ZHANG Lei, SHOJI M. Aperiodic bubble formation from a submerged orifice[J]. Chemical engineering science, 2001, 56(18): 5371-5381. DOI:10.1016/S0009-2509(01)00241-X ( 0) 0)
|
| [4] |
AYBERS N M, TAPUCU A. Studies on the drag and shape of gas bubbles rising through a stagnant liquid[J]. Wärme - und stoffübertragung, 1969, 2(3): 171-177. DOI:10.1007/BF00751164 ( 0) 0)
|
| [5] |
SABERI S, SHAKOURZADEH K, BASTOUL D, et al. Bubble size and velocity measurement in gas-liquid systems: application of fiber optic technique to pilot plant scale[J]. The Canadian journal of chemical engineering, 1995, 73(2): 253-257. DOI:10.1002/cjce.v73:2 ( 0) 0)
|
| [6] |
DE LASA H, LEE S L P, BERGOUGNOU M A. Bubble measurement in three-phase fluidized beds using a u-shaped optical fiber[J]. The Canadian journal of chemical engineering, 1984, 62(2): 165-169. DOI:10.1002/cjce.v62:2 ( 0) 0)
|
| [7] |
MARTÍNEZ MERCADO J, CHEHATA GÓMEZ D, VAN GILS D, et al. On bubble clustering and energy spectra in pseudo-turbulence[J]. Journal of fluid mechanics, 2010, 650: 287-306. DOI:10.1017/S0022112009993570 ( 0) 0)
|
| [8] |
PRASSER H M. Novel experimental measuring techniques required to provide data for CFD validation[J]. Nuclear engineering and design, 2008, 238(3): 744-770. DOI:10.1016/j.nucengdes.2007.02.050 ( 0) 0)
|
| [9] |
SCHMIDT I, MINCEVA M, ARLT W. Selection of stationary phase particle geometry using X-ray computed tomography and computational fluid dynamics simulations[J]. Journal of chromatography A, 2012, 1225: 141-149. DOI:10.1016/j.chroma.2011.12.072 ( 0) 0)
|
| [10] |
KULKARNI A A, JOSHI J B, KUMAR V R, et al. Application of multiresolution analysis for simultaneous measurement of gas and liquid velocities and fractional gas hold-up in bubble column using LDA[J]. Chemical engineering science, 2001, 56(17): 5037-5048. DOI:10.1016/S0009-2509(01)00191-9 ( 0) 0)
|
| [11] |
MAJUMDER S K, KUNDU G, MUKHERJEE D. Bubble size distribution and gas–liquid interfacial area in a modified downflow bubble column[J]. Chemical engineering journal, 2006, 122(1/2): 1-10. ( 0) 0)
|
| [12] |
HONKANEN M, ELORANTA H, SAARENRINNE P. Digital imaging measurement of dense multiphase flows in industrial processes[J]. Flow measurement and instrumentation, 2010, 21(1): 25-32. DOI:10.1016/j.flowmeasinst.2009.11.001 ( 0) 0)
|
| [13] |
LECUONA A, SOSA P A, RODRÍGUEZ P A, et al. Volumetric characterization of dispersed two-phase flows by digital image analysis[J]. Measurement science and technology, 2000, 11(8): 1152-1161. DOI:10.1088/0957-0233/11/8/309 ( 0) 0)
|
| [14] |
MIKAELIAN D, LARCY AÉLIE, DEHAECK S, et al. A new experimental method to analyze the dynamics and the morphology of bubbles in liquids: application to single ellipsoidal bubbles[J]. Chemical engineering science, 2013, 100: 529-538. DOI:10.1016/j.ces.2013.04.013 ( 0) 0)
|
| [15] |
KESHAVARZI G, PAWELLA R S, BARBER T J, et al. Transient analysis of a single rising bubble used for numerical validation for multiphase flow[J]. Chemical engineering science, 2014, 112: 25-34. DOI:10.1016/j.ces.2014.02.027 ( 0) 0)
|
| [16] |
HONKANEN M, SAARENRINNE P, STOOR T, et al. Recognition of highly overlapping ellipse-like bubble images[J]. Measurement science and technology, 2005, 16(9): 1760-1770. DOI:10.1088/0957-0233/16/9/007 ( 0) 0)
|
| [17] |
LAGE L C P, ESPÓSITO R O. Experimental determination of bubble size distributions in bubble columns: prediction of mean bubble diameter and gas hold up[J]. Powder technology, 1999, 101(2): 142-150. DOI:10.1016/S0032-5910(98)00165-X ( 0) 0)
|
| [18] |
WONGSUCHOTO P, CHARINPANITKUL T, PAVASANT P. Bubble size distribution and gas–liquid mass transfer in airlift contactors[J]. Chemical engineering journal, 2003, 92(1/2/3): 81-90. ( 0) 0)
|
| [19] |
RAKOCZY R, MASIUK S. Experimental study of bubble size distribution in a liquid column exposed to a rotating magnetic field[J]. Chemical engineering and processing: process intensification, 2009, 48(7): 1229-1240. DOI:10.1016/j.cep.2009.05.001 ( 0) 0)
|
| [20] |
HANSELMANN W, WINDHAB E. Flow characteristics and modelling of foam generation in a continuous rotor/stator mixer[J]. Journal of food engineering, 1998, 38(4): 393-405. DOI:10.1016/S0260-8774(98)00129-0 ( 0) 0)
|
| [21] |
AL-OUFI F M, RIELLY C D, CUMMING I W. An experimental study of gas void fraction in dilute alcohol solutions in annular gap bubble columns using a four-point conductivity probe[J]. Chemical engineering science, 2011, 66(23): 5739-5748. DOI:10.1016/j.ces.2011.03.061 ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


