对转螺旋桨（对转桨）是一种组合推进器，由２个常规螺旋桨（定义为前桨和后桨）装于同心的内外双轴上，前后桨旋向相反。对转桨具有良好的自身扭矩平衡性能，作为主推进器广泛应用于对横滚扭矩十分敏感的回转体外形水下航行器和鱼雷。对转桨的水动力性能直接影响着推进器效率、空化、噪声和振动等指标，关系着对转桨设计方案的优劣。对转桨的前后桨间具有强烈的相互作用，后桨工作在前桨的尾流中，前桨又受到后桨的抽吸作用。因此，精确预报对转桨的定常、非定常水动力性能一直是对转桨研究的热点和难点。近几十年来，国内外学者开展了多项关于对转桨水动力性能方面的研究工作，从模型试验、势流理论预报、计算流体力学（CFD）方法预报、船−对转桨相互干扰等多个角度发展、丰富了对转桨的研究方法。Miller^[1]针对对转桨在均匀流和非均匀流中的工况下，进行了水动力性能模型试验；Tsakonas^[2]和Yang^[3−4]采用非定常升力面理论、Liu^[5]采用面元法进行了对转桨的定常及非定常水动力性能预报工作，但预报结果精度有待进一步提高；Kinnas等^[6−7]通过势流理论（涡格法或面元法）与CFD方法中的RANS求解器（轴对称2D或非轴对称3D）耦合迭代计算，模拟了对转桨性能及周围流场，开辟了对转桨流场模拟的新思路；张涛^[8−9]和王展智^[10]借助计算流体力学中的RANS方法研究了对转桨水动力性能预报过程中参数设置对预报精度的影响，得到了一些有助于提高计算精度和效率的结论；Sasaki^[11]和Grassi^[12]进行了对转桨设计方法和模型试验方法的研究工作；近期，Yasuhiko等^[13−15]针对船体与对转桨之间的相互干扰开展了一系列研究工作。

本文发展了一种对转桨非定常水动力性能的预报方法。该方法基于雷诺平均纳维−斯托克斯（RANS）方程并结合SSTk-ω湍流模型，采用滑移网格模型和螺旋桨周围区域的精细化网格划分策略，处理前后桨之间的相互干扰。利用该方法，开展了美国泰勒水池对转桨方案和某型水下高速航行体对转桨方案的非定常水动力性能数值预报，结合试验结果进行对比分析，验证本文方法的可行性和准确性。

1 数值预报模型 1.1 控制方程

考虑对转桨在不可压缩黏性流体中旋转，运动满足三维雷诺平均纳维−斯托克斯（RANS）方程：

$ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}(\rho {u_i}) = 0\\ $

$ \frac{\partial }{{\partial t}}(\rho {u_i}) + \frac{\partial }{{\partial {x_j}}}(\rho {u_i}{u_j}) = - \frac{{\partial p}}{{\partial {x_i}}} \!+\! \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}} \!+ \!{F_i} \!+\! \frac{\partial }{{\partial {x_j}}}( - \rho \overline {{u_i}^\prime {u_j}^\prime } ) $

式中： $\rho $ 为流体密度；t为时间；u_i和u_j为速度矢量；p为静压力； ${\tau _{ij}}$ 为剪切应力；x_i和x_j分别为i和j方向上的位置位标；F_i为i方向上的体积力； $-\rho \overline {{u_i}^\prime {u_j}^\prime } $ 为雷诺应力项。

要使上述方程封闭，必须对未知的雷诺应力项作某种假设。本文选取SST k−ω湍流模型^[16]，把雷诺应力项中的脉动值与时均值联系起来，封闭方程。该湍流模型综合了标准k−ω模型在近壁面区和标准k−ε模型在远场区计算的优点，在流场模拟中具有较高的计算精度和算法稳定性。

1.2 模型离散化与边界条件

选取与对转桨共轴的圆柱体作为计算域，如图1所示。根据以往对螺旋桨性能数值模拟的经验，确定计算域尺寸为：圆柱体外边界直径为5倍前桨直径，入口在前桨盘面上游4倍前桨直径处，出口在后桨盘面下游8倍前桨直径处。将计算域分成多个子域分别进行合适的网格结构划分，以保证较高的网格质量和较少的网格数量。由于对转桨复杂的几何外形和前后桨间极小的轴向间隙，对紧邻对转桨的区域进行结构化网格划分存在较大的难度，也难以保证网格质量。因此，本文采用结构与非结构多块混合网格划分方法，针对对转桨附近的形状复杂流域采用非结构化网格划分，对于几何形状十分规则的对转桨外域流场则划分高质量的结构化网格。

螺旋桨叶片壁面生成4层边界层网格，增长率为1.15，精确设置螺旋桨叶片壁面第1层网格的高度，使该处的Y+值在30~90。为较精确地捕捉前桨的尾流，在前后桨之间的区域加密网格。此外，为了尽可能地减小网格离散所带来的误差、真实模拟前后桨间的相互影响，对前后桨滑移网格交界面附近进行特殊处理。具体处理策略是，交界面附近网格采用结构化网格划分，前桨与后桨各自的交界面网格节点一一对应，并且网格周向划分时考虑与非定常数值模拟采用的时间步长相匹配，使前后桨每经过一个时间步长的计算（即每转过一个角度），相互交界面的网格节点依然重合。该网格划分策略有望在前后桨计算子域通过交界面进行数据传递更新（如流场的速度、压力、湍动能等物理量）时，减小数值误差。

基于螺旋桨的轴对称特性，可将包含螺旋桨的计算子域进一步按螺旋桨叶片数目切分成更小的子块。仅需对其中的一个子块划分网格，再按螺旋桨叶片数目周向旋转复制合并，即可得到包含螺旋桨计算子域的网格，此操作可保证每个螺旋桨叶片及其附近网格的严格一致、减小网格离散带来的计算误差。

如图1所示，入口边界设为速度入口；出口边界设为压力出口；在旋转坐标系下，桨叶及桨毂表面均采用无滑移固壁条件。本文数值求解过程基于商用计算流体力学软件FLUENT，计算参数设置如表1所列。

2 结果与讨论

本文选取2个对转桨方案进行水动力性能预报，以验证本文预报方法的可行性和准确性。方案A^[1]为美国泰勒水池的对转桨方案，该方案较为特殊，为研究前后桨相互干扰而专门将前后桨叶数设计为相等（均为4叶）情况，具有较为详尽的试验数据。方案B来源于某高速水下航行器的主推进器，具有大毂径和多叶片的特征。2个方案的主要几何特征如表2所列。

2.1 方案A

对于方案A，按照前面所述的网格划分方法，整个计算域约500万网格；其中包含前后桨的2子域的网格数量约为450万。为与相应的试验条件保持一致，设定前后桨的转速N为720 r/min，并保持不变，进速因数J的变化由改变来流速度V实现。

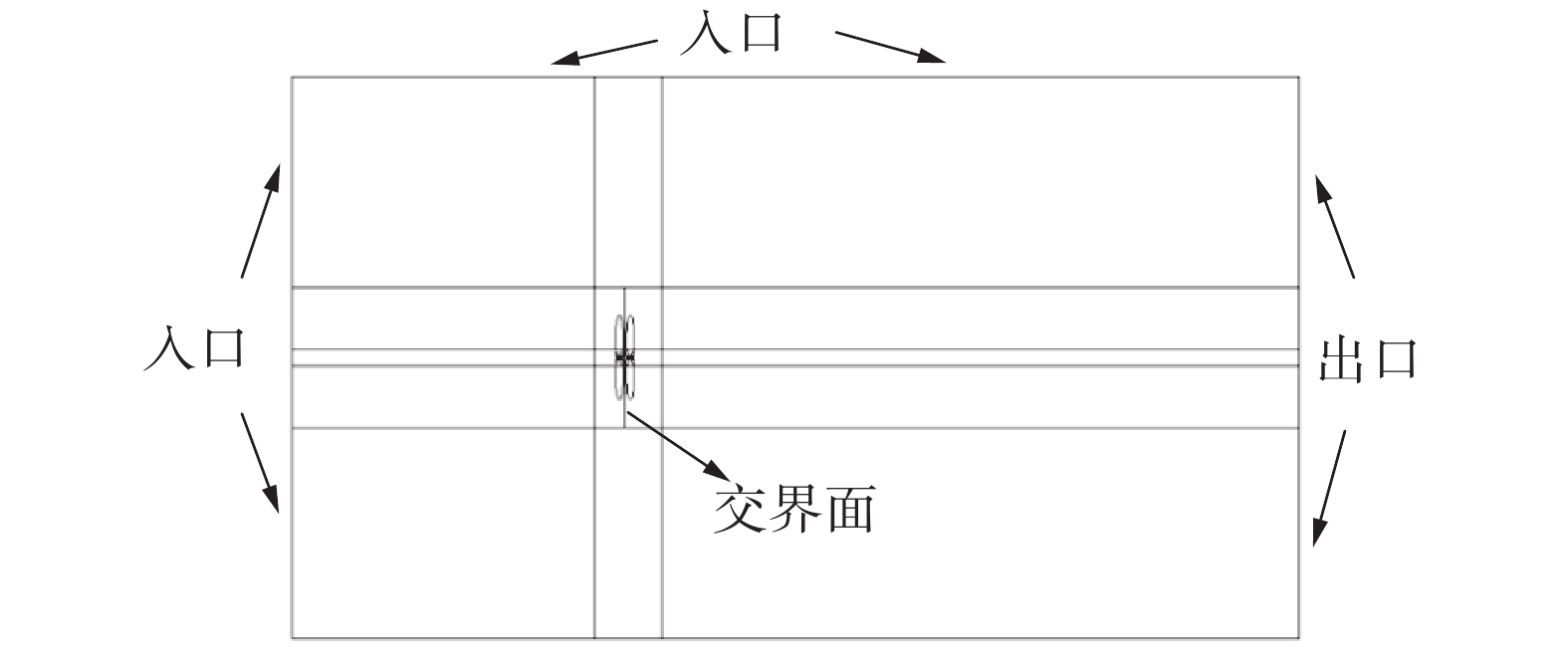
选取计算时间步长Δt=1/(12N)，该时间步长对应前后桨各自旋转0.5°，因前后桨旋向相反，故在1个时间步长后，前后桨的相位错开1°。如图2所示，将前后桨交界面的网格沿周向均匀划分为360份，则每个网格节点都与同一半径处的相邻节点在周向上相差1°。因此，在每一个计算时间步长完成即前后桨相位每一次错开1°后，前桨交界面处的所有网格节点均与后桨交界面处的网格节点重合。这样可最大程度减小前后桨计算子域之间通过交界面进行数据传递更新时插值所带来的数值误差。

关于对转桨，推力和扭矩的脉动频率为：

$ f = {f_n} \times \left( {{m_F}{Z_F} + {m_A}{Z_A}} \right) $

且有

$ {{m_F}{Z_F} = {m_A}{Z_A}} $

式中：f_n为轴频；Z_F和Z_A分别为前后桨叶数；m_F和m_A为正整数。

具体到方案A，当m_F=m_A=1时，最低脉动频率f_min=8f_n。这说明，当螺旋桨旋转一周时，推力和扭矩经历8个周期的脉动。图3所示为对转桨在进速系数J=1.1的工况下，一个旋转周期内的前后桨瞬时推力因数和扭矩因数曲线。观察该曲线可知，推力因数和扭矩因数每45°重复一次，与上述8个周期脉动相对应。此外从图3还可看出，前桨脉动幅值明显高于后桨，前桨推力与扭矩的脉动幅值约为其时均值的45%，而后桨仅约为17%。

表3、4所列为一阶脉动频率（对应8倍轴频）、二阶脉动频率（对应16倍轴频）下，推力因数与扭矩因数脉动幅值的计算结果与试验结果对比。从中可以归纳出，所有数值预报均低估了推力和扭矩的实际脉动幅值，而且后桨的预报结果较前桨更差。具体到数据，一阶脉动频率下，前桨与试验数据的最大相对误差为−11.5%，而后桨为−18.8%；二阶脉动频率下，前桨与试验数据的最大相对误差为−29.7%，而后桨为−37.2%；该数据优于其他研究的预报结果。对转桨非定常脉动幅值预报结果误差较大的原因，归结为前桨尾流强度的低估或过大的数值耗散，提高网格精度或减小计算时间步长可以改善减小误差。

2.2 方案B

对于方案B，按照前面所述的网格划分方法，整个计算域约800万网格，其中包含前后桨的2个子域的网格数量约为720万。为与相应的试验条件保持一致，设定前后桨的转速N为1 500 r/min，并保持不变，进速因数J的变化由改变来流速度V实现。

方案B为前桨7叶、后桨9叶，根据公式 $f = {f_n} \times \left( {{m_F}{Z_F} + {m_A}{Z_A}} \right)$ 可知，推力及扭矩的最低脉动频率为 ${f_{\mathit{\min}}} = 126{f_n}$ ，远高于方案A。从 ${f_{\mathit{\min}}} = 126{f_n}$ 可知，当螺旋桨旋转一周时，推力和扭矩经历126个周期的脉动，这意味着当对转桨方案B转过360/126=2.86°时，前后桨的推力及扭矩就重复一次。根据奈奎斯特采样定律，252个数据点即可表示126个周期的变化规律。为了获得更精确的采样结果，常规方法会选择5个数据点表达1个周期的变化，则126个周期需要630个数据采样点。因此，本研究选取合适的计算时间步长，使非定常计算每一步后，前后桨旋转错开0.5°，此时对应了对转桨旋转一周时具有720个数据点，保证了方案B高脉动频率特征的精确表达。

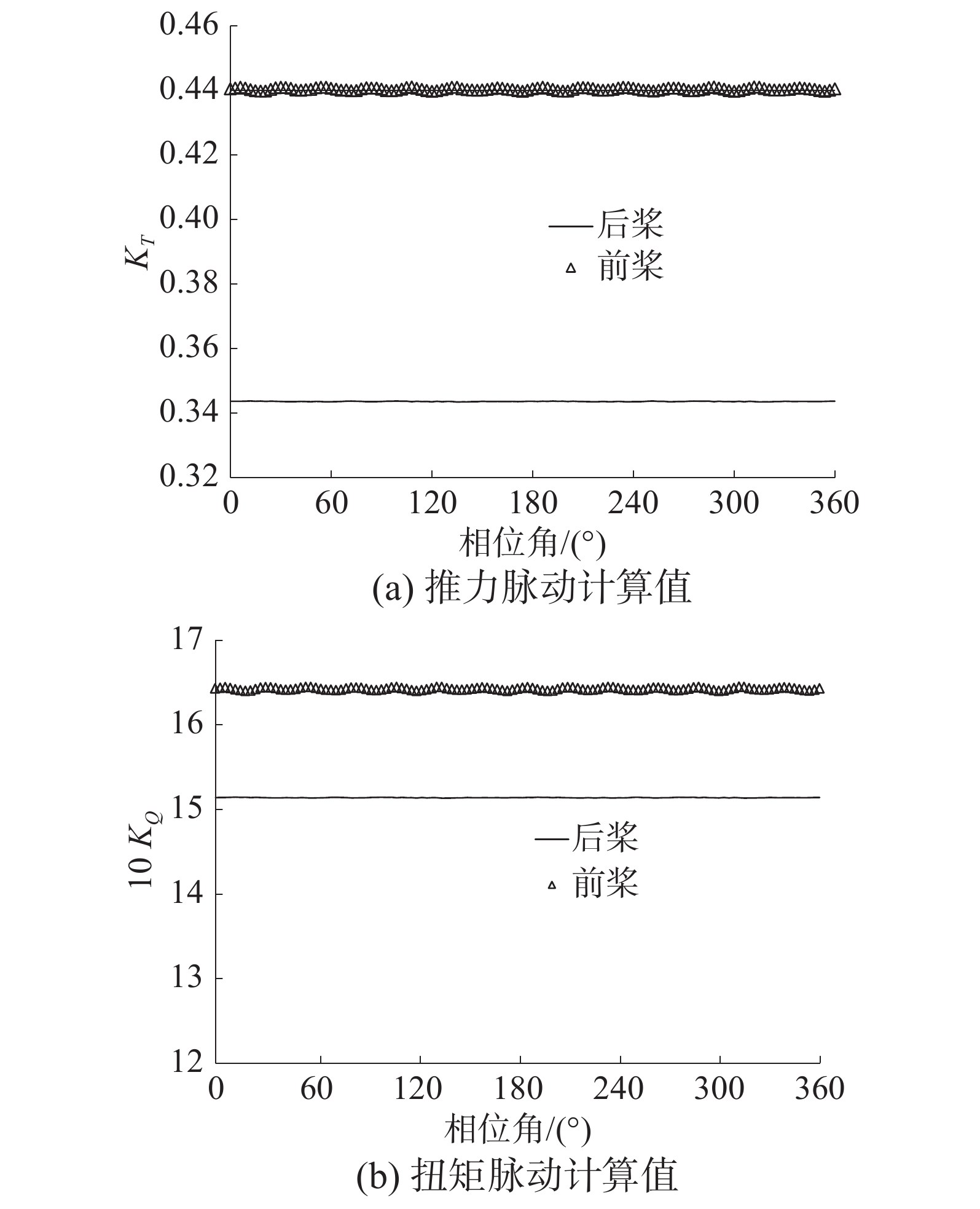
对转桨方案B的桨叶数远多于方案A，其载荷的脉动幅值也会低于方案A。图4所示为对转桨在设计点工况下，一个旋转周期内的前后桨瞬时推力因数和扭矩因数曲线。

从图4曲线可以看出，前后桨推力与扭矩的脉动幅值均小于其时均值的0.5%。这表明，对于具有高脉动频率的对转桨方案而言，因其载荷的脉动幅值非常小而易受数值计算误差的影响，精确模拟其非定常水动力性能存在较大难度。

图5所示为对转桨方案B前后桨及整体的推力因数与扭矩因数时均值（即敞水性能）的计算与试验结果对比。从图中可以看出，计算结果较试验结果而言，前桨推力偏高、后桨推力偏低，前后桨扭矩均偏高；前后桨推力值最大误差为6.43%，前后桨扭矩值最大误差为4.4%；对转桨总推力、总扭矩的最大误差分别为1.15%和4.21%；敞水效率偏低，在进速因数范围内最大误差为3.95%。

3 结论

本文研究了一种基于RANS方法的对转桨非定常水动力性能的数值预报方法。为验证本文方法的可行性和准确性，开展了美国泰勒水池对转桨方案和某型水下高速航行体对转桨方案的非定常水动力性能数值预报研究，通过预报与试验结果的对比分析，得到以下结论：

1）对于像方案A这类前后桨叶数相同的对转桨而言，前后桨的相互干扰较强，且干扰脉动频率较低。本文提出的对转桨附近区域考虑具体计算时间步长的网格划分策略，可以较好地捕捉前桨的尾流、较精确地模拟前后桨之间的相互干扰，从而提高了对转桨非定常水动力性能的预报精度。

2）对于像方案B这类实际工程中常用的前后桨叶数不同的对转桨而言，前后桨的相互干扰较弱，且干扰脉动频率较高。非定常脉动幅值小于定常力的0.5%，在工程应用中可以忽略。经验证，本文的预报方法同样适用于对转桨敞水性能的高精度预报。