2. 中国地震局工程力学研究所,黑龙江 哈尔滨 150080
2. Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, China
斜坡式防波堤是为阻断波浪冲击、围护港池、维持水面平稳而修建的海洋结构。尤其是对于核电站海防工程,斜坡式防波堤更是不可或缺的重要组成部分。福岛核电站事故发生后,环保部发布新规,核电站(包括其海防工程)建设必须考虑地震的影响。而且,波浪作用是斜坡式防波堤结构的常遇环境作用,地震发生时斜坡式防波堤结构会同时受到地震和波浪荷载的共同作用, 所以有必要对斜坡式防波堤结构在地震与波浪共同作用下的动力特性进行研究。近年来,国内外学者针对斜坡式防波堤结构陆续开展了这方面的研究[1−4]。
武崇福等[5]利用Ansys有限元软件对高桩承台−土−上部结构在波浪和地震共同作用下的受力和变形进行了分析。何晓宇等[6]建立了小尺度桩柱在波浪与地震共同作用下的运动方程,分析了流固耦合效应对结构响应的影响,以及这种影响随桩柱的工作水深和波浪参数的变化规律。李忠献等[7]建立了地震和波浪联合作用下深水桥梁动力响应分析方法,并对深水桥梁在地震和波浪联合作用下的动力响应进行了分析,阐明了水与桥墩动力相互作用对深水桥梁动力响应的影响。柳国环等[8]结合地震和波浪力2种激励分析了海上复合筒型基础风力发电结构体系的动力特性,并对结构体系动力反应和对波浪力的敏感性进行了研究。文献[9−10]分别对典型单桩海上风机结构和空间导管架式海洋平台结构在地震与波浪联合作用下的动力响应进行了深入研究。Chaudhary等[11]提出了一种分析斜坡式防波堤稳定性的方法,并对斜坡式防波堤在地震和海啸联合作用下的滑移与倾覆稳定性进行了分析。柳春光等[12]对近年来跨海桥梁结构在承受波浪、海流、地震联合作用下的理论、数值、试验研究与进展进行了综述,并对桥梁结构考虑波浪、海流作用的水下振动台试验的发展进行了展望。
斜坡式防波堤结构在地震作用下会产生变形和运动,这种变形和运动会影响其周围海水的运动,而海水的运动又以动水压力的形式反作用于斜坡式防波堤结构。在本文中,波浪荷载一方面以动水压力的形式作用于斜坡式防波堤结构海面以下部位,另一方面以波浪力或规则波的方式作用于斜坡式防波堤结构海面以上部位(如前后挡浪墙)。利用ABAQUS有限元软件建立了地基−斜坡式防波堤结构有限元模型,验证了模型的正确性,并对斜坡式防波堤在地震以及地震和波浪共同作用下的动力响应进行了仿真研究。本文的研究为斜坡式防波堤结构的工程设计和安全评价提供了有益参考。
1 基本方程地震和波浪共同作用下斜坡式防波堤结构动力学方程可以表示为:
| $\begin{array}{l} { M}{{\ddot u}_s}\left( t \right) + { C}{{\dot u}_s}\left( t \right) + { K}{u_s}\left( t \right) = - { M}{{\ddot u}_g}\left( t \right) + p + P \end{array} $ |
式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;
动水压力可以表示为[13]:
| $\begin{array}{l} {p_{x = 0}}\left( {y,t} \right) = \displaystyle\frac{{4{{\ddot u}_0}\rho }}{{\text π} }\cos \omega t\sum\limits_{n = 1,3,5, \cdots }^\infty {\frac{1}{{\sqrt {\lambda _n^2 - \displaystyle\frac{{{\omega ^2}}}{{{c^2}}}} }}\sin {\lambda _n}y} \end{array} $ |
式中:
斜坡式防波堤波浪力可从波浪的爬高角度,根据爬高以及爬高水体的厚度来分析波浪力,计算公式如下[14]:
| $ \left\{ {\begin{aligned} & {{P_{{h_1}}} = \alpha \rho g{h_1}}\\ & {{h_1} = {h_w}\left( {1 - \frac{Z}{{{R_u}}}} \right)}\\ & {\alpha = 2.9{{\left( {\frac{{{R_u}}}{{{H_u}}}\cos \;\; \beta } \right)}^2}} \end{aligned}} \right. $ |
式中:
在海水和斜坡式防波堤结构边界处应满足几何相容条件和力的平衡条件,即:
几何相容条件
| ${u_q} - {u_s} = 0 \;\; \left( {{\text{在}}{S_{qs}}{\text{上}}} \right)$ |
力的平衡条件
| ${T_q} + {T_s} = 0 \;\; \left( {{\text{在}}{S_{qs}}{\text{上}}} \right)$ |
式中:
本文研究的是某核电工程中起防波作用的斜坡式防波堤。整个斜坡式防波堤结构主要由10~100 kg的块石堆砌而成,总长113 m,高12.7 m,两侧均设置有斜坡。根据工程实际,向海侧斜坡较多,坡比为1∶2或1∶3;背海侧斜坡较少,坡比为1∶3或1∶2.5,且向海侧设置了护坡及缓冲平台,以最大限度缓和海水对斜坡式防波堤结构的冲击作用。斜坡式防波堤结构上部设置挡浪墙,斜坡式防波堤结构和地基土层的整体断面如图1所示[3],地基各土层参数如表1所示。

|
Download:
|
| 图 1 斜坡式防波堤结构和地基土层的整体断面示意 | |
|
|
表 1 土层参数 |
根据图1,先建立斜坡式防波堤的几何模型。再通过使用ABAQUS有限元软件的property功能模块对斜坡式防波堤结构和地基土层每个部分进行材料参数的设置。
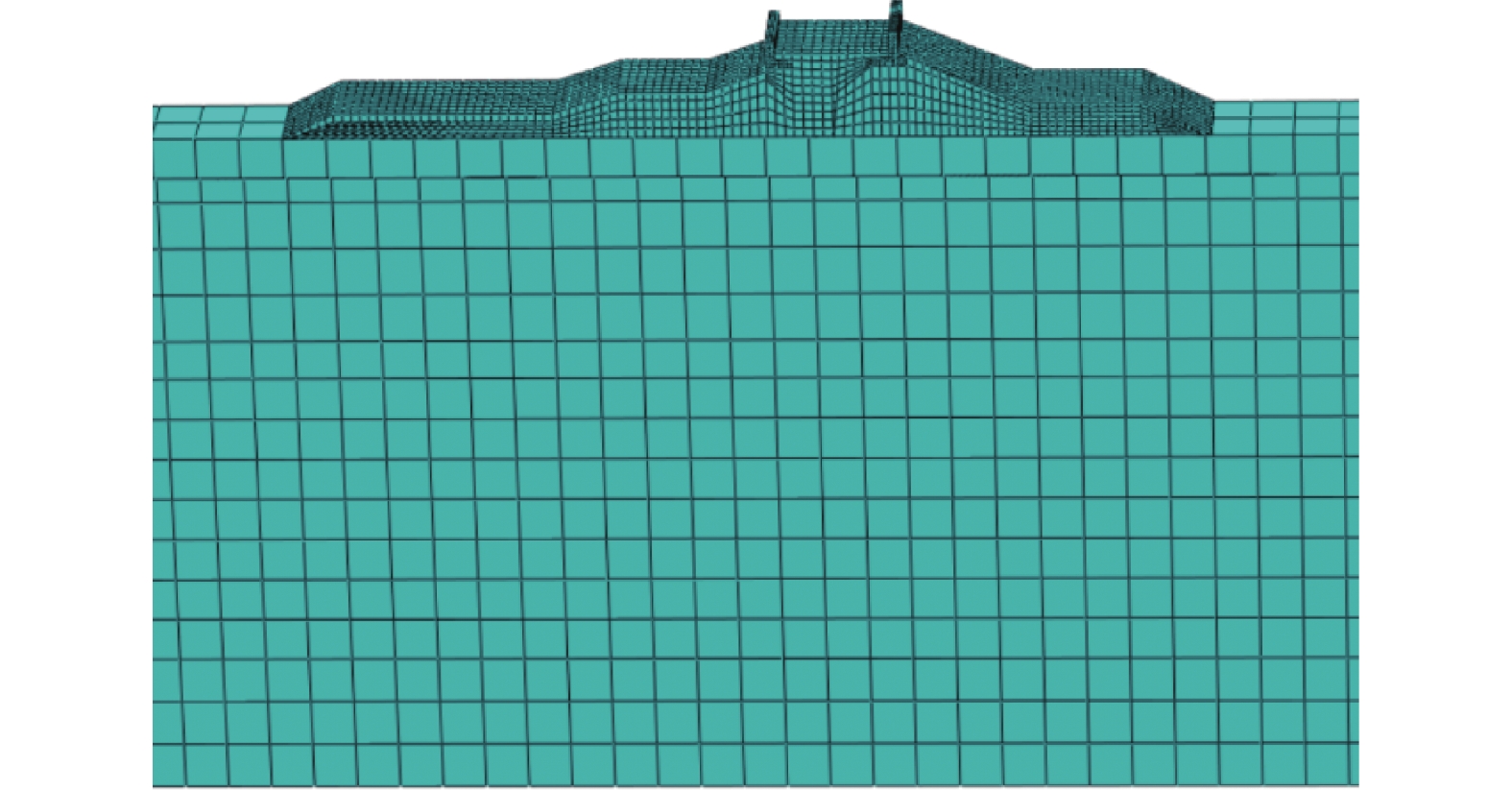
为了减少边界的影响,将海水和地基土的长度设置为斜坡式防波堤宽的6倍。地基中各个土层之间面−面设置tie约束进行绑定约束,斜坡式防波堤结构与土层之间需设置接触,同时还需考虑斜坡式防波堤主体与护坡、主体与挡浪墙之间的相互作用。其中接触需在接触模型使用罚函数的方式来确定面−面间的切向力学性质,摩擦系数取0.4,同时添加法向方向,使用硬接触。单元均选用8节点减缩积分单元C3D8R,划分网格后的模型如图2所示。
|
Download:
|
| 图 2 模型网格划分 | |
本文采用了文献[3]中的本构模型、模态以及阻尼。地震发生过程中,由于地面的不断运动,土体会随之出现弹塑性应变,所以土体及堆石采用了Drucker-Prager弹塑性模型。挡浪墙其材质为混凝土材质,其本构分为2个阶段,其一的弹性阶段使用线弹性模型,其二的塑性阶段使用混凝土损伤塑性模型。
地震发生时,因为阻尼的存在,在现实状态下地基−斜坡式防波堤结构会由于振动持续消耗能量。在实际分析中,通常采用的是瑞利阻尼。
瑞利阻尼的矩阵形式可写为
| ${ C} = \alpha { M} + \beta { K}$ |
式中
| $\alpha = \frac{{2{\omega _{\text{i}}}{\omega _j}({\xi _i}{\omega _j} - {\xi _j}{\omega _i})}}{{\omega _j^2 - \omega _i^2}}$ |
| $\beta = \frac{{2({\xi _j}{\omega _j} - {\xi _i}{\omega _i})}}{{\omega _j^2 - \omega _i^2}}$ |
式中
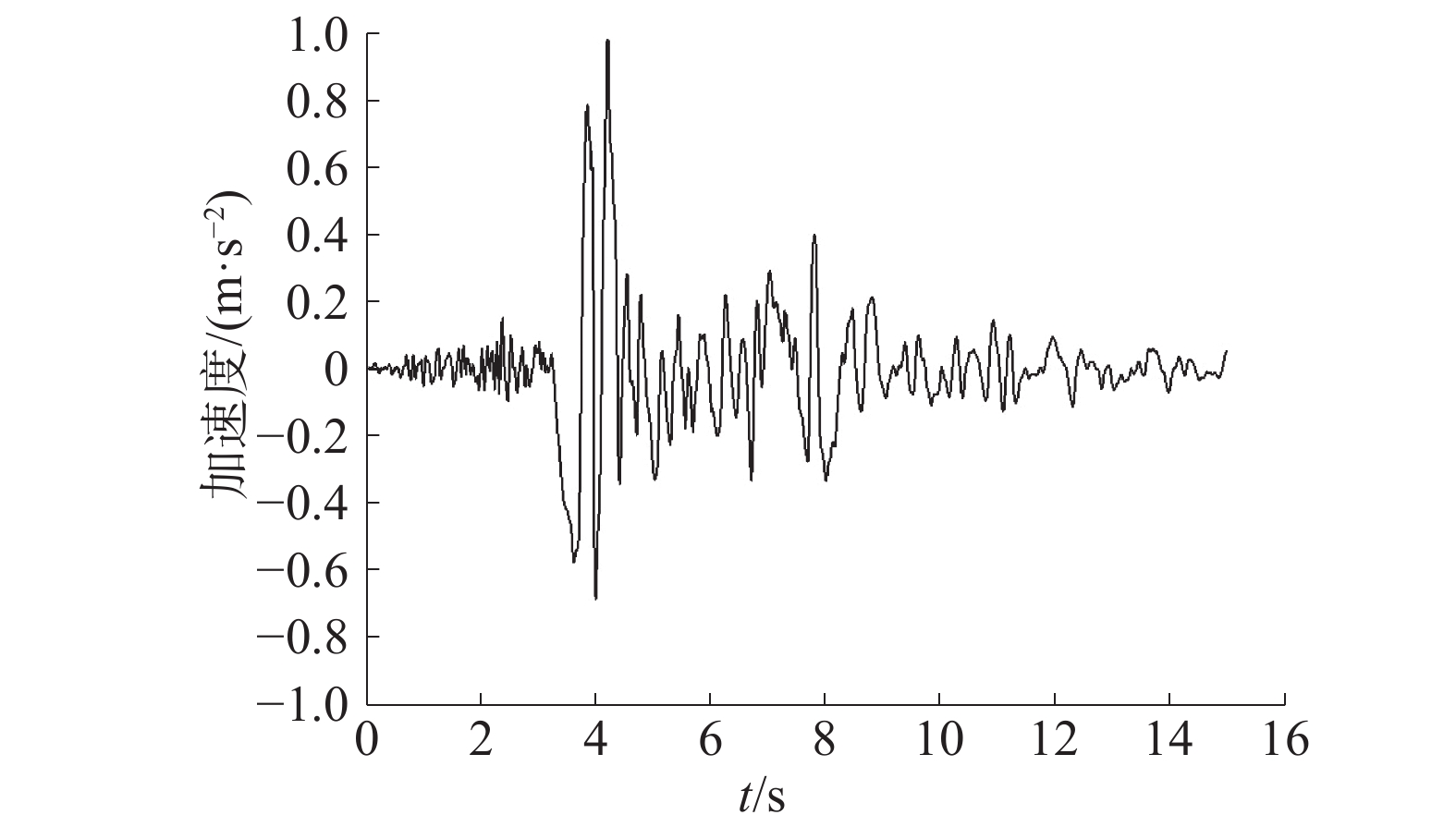
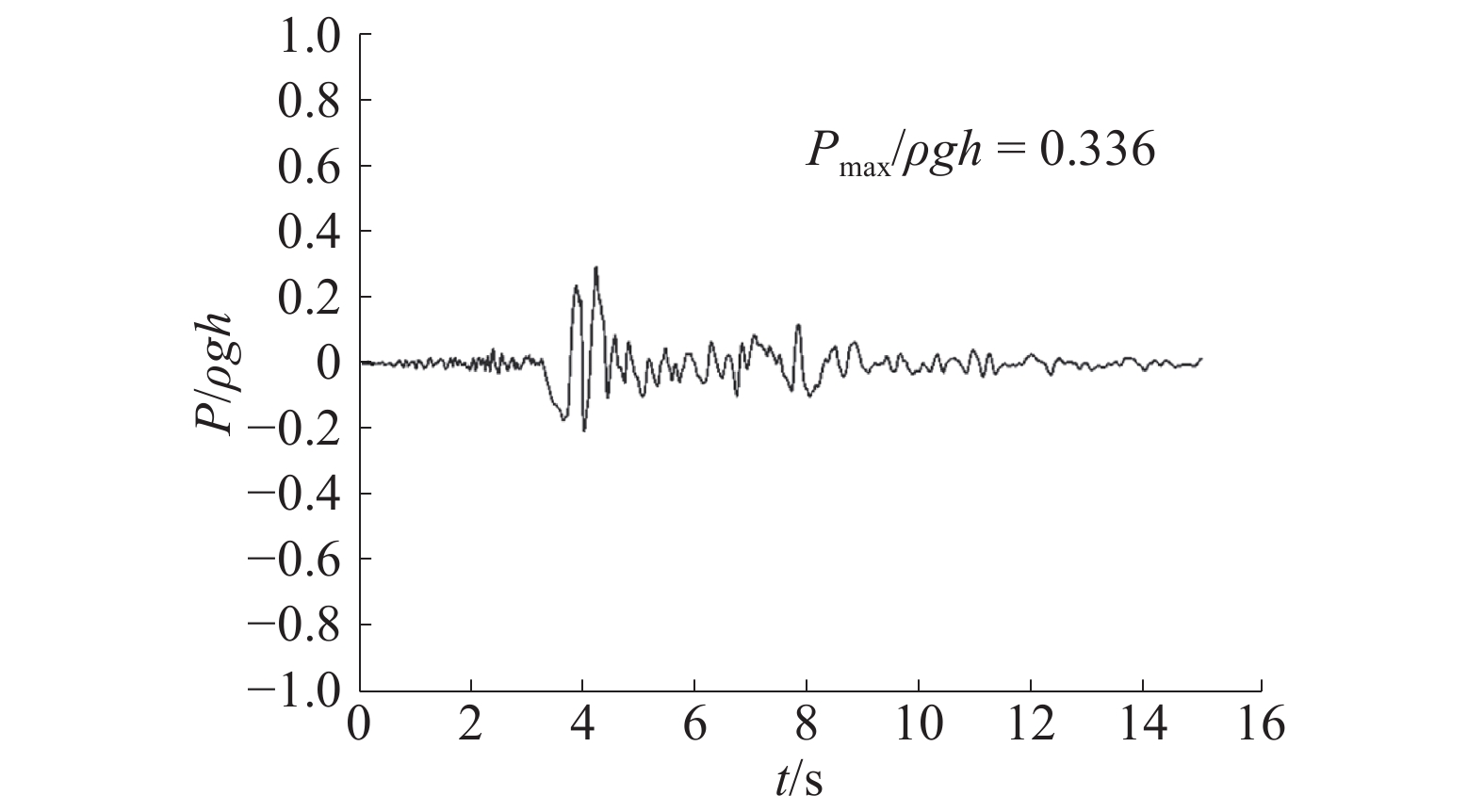
荷载包括重力荷载、水压力荷载、地震荷载、波浪荷载。文献[15]指出,目前工程抗震设计一般采用无质量地基均匀输入模式,即将地震加速度直接输入到基底上,此法概念明确、处理方便且具有合理性。本文地震荷载如图3所示,施加在基底,并设置加速度边界条件,仅考虑水平地震荷载作用。水压力荷载包括静水压力荷载和动水压力荷载,静水压力一直存在不可忽略,施加在地基和斜坡式防波堤的向海侧上;动水压力是由地震引起且作用于水体和防波堤的接触面上。图4给出了当
|
Download:
|
| 图 3 Frulli地震波加速度时程曲线 | |
|
Download:
|
|
图 4 |
|
本文采用了文献[3]中的斜坡式防波堤结构,建立了相应的有限元模型,选用了文献[3]中的Friuli地震波进行了动力响应分析,其残余变形如表2所示。
|
|
表 2 斜坡式防波堤的残余变形与文献[3]比较 |
通过表2可以看出,本文建立的有限元模型,其计算结果与文献[3]相比误差较小。通过此模型研究地震和波浪共同作用下斜坡式防波堤的动态响应问题是可行的。
3.3 地震和波浪共同作用下斜坡式防波堤的动力响应在前述地震作用下斜坡式防波堤的动力响应研究的基础上,进一步对地震和波浪共同作用下斜坡式防波堤的动力响应进行研究。
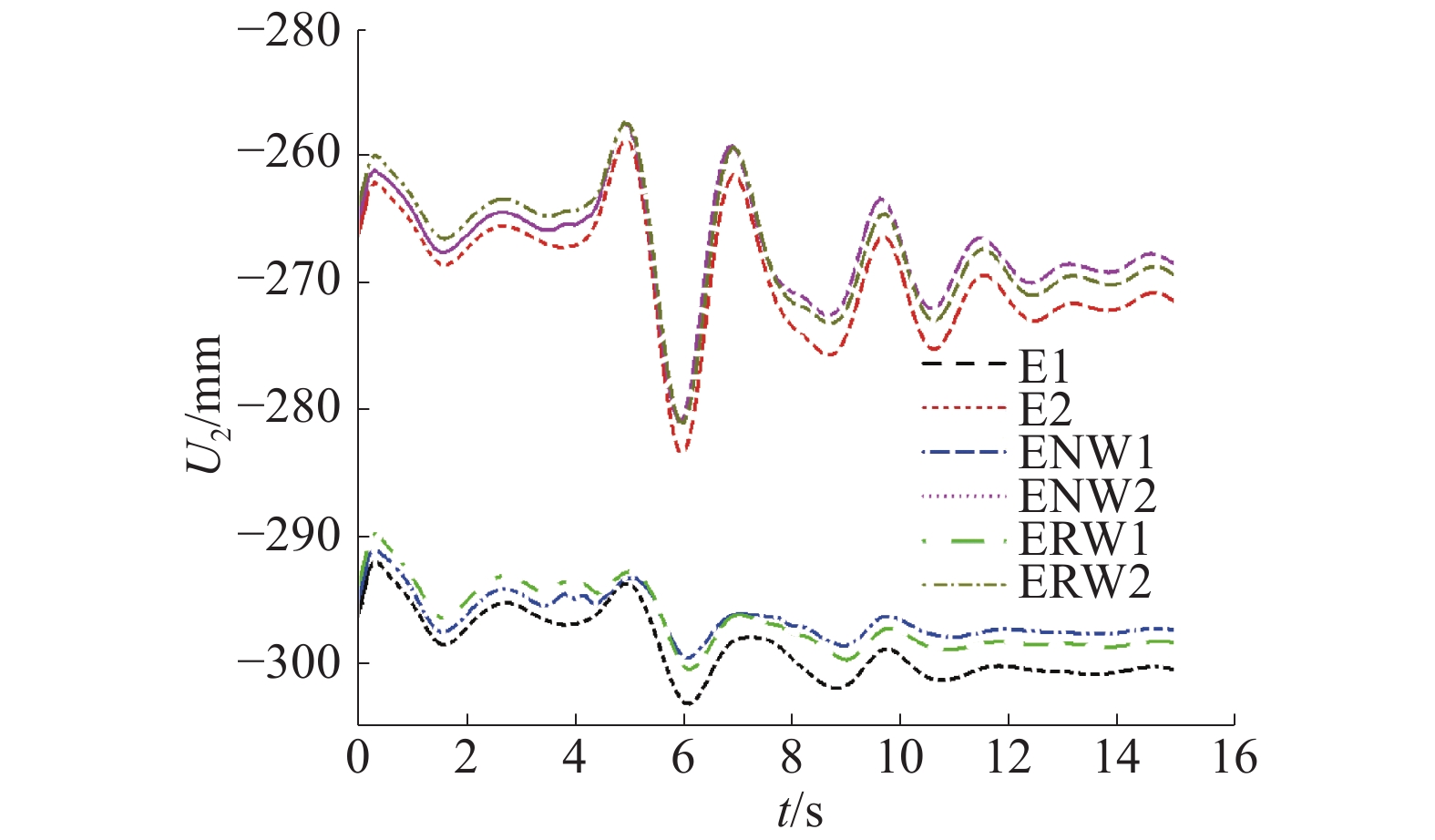
图5~10分别给出了在不同荷载作用下,斜坡式防波堤面内水平x方向、面内竖直y方向和垂直于面内z方向上关键点的动态位移响应时程曲线。图中,E表示地震作用;ENW表示地震和总波浪力共同作用;ERW表示地震和规则波共同作用。

|
Download:
|
| 图 5 x方向1点和2点位移曲线 | |

|
Download:
|
| 图 6 x方向5点和6点位移曲线 | |
|
Download:
|
| 图 7 y方向1点和2点位移曲线 | |
|
Download:
|
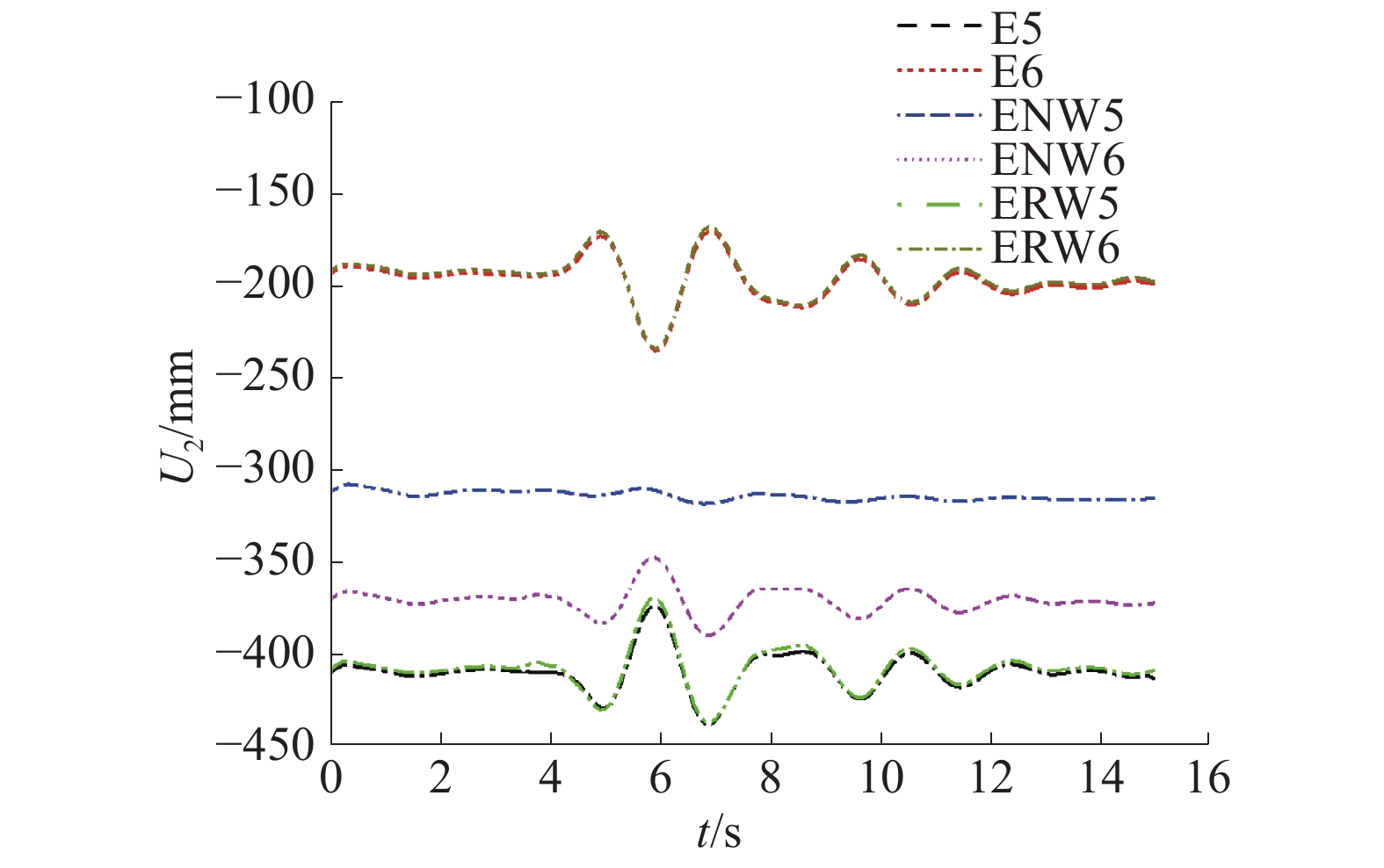
| 图 8 y方向5点和6点位移曲线 | |

|
Download:
|
| 图 9 z方向1点和2点位移曲线 | |
|
Download:
|
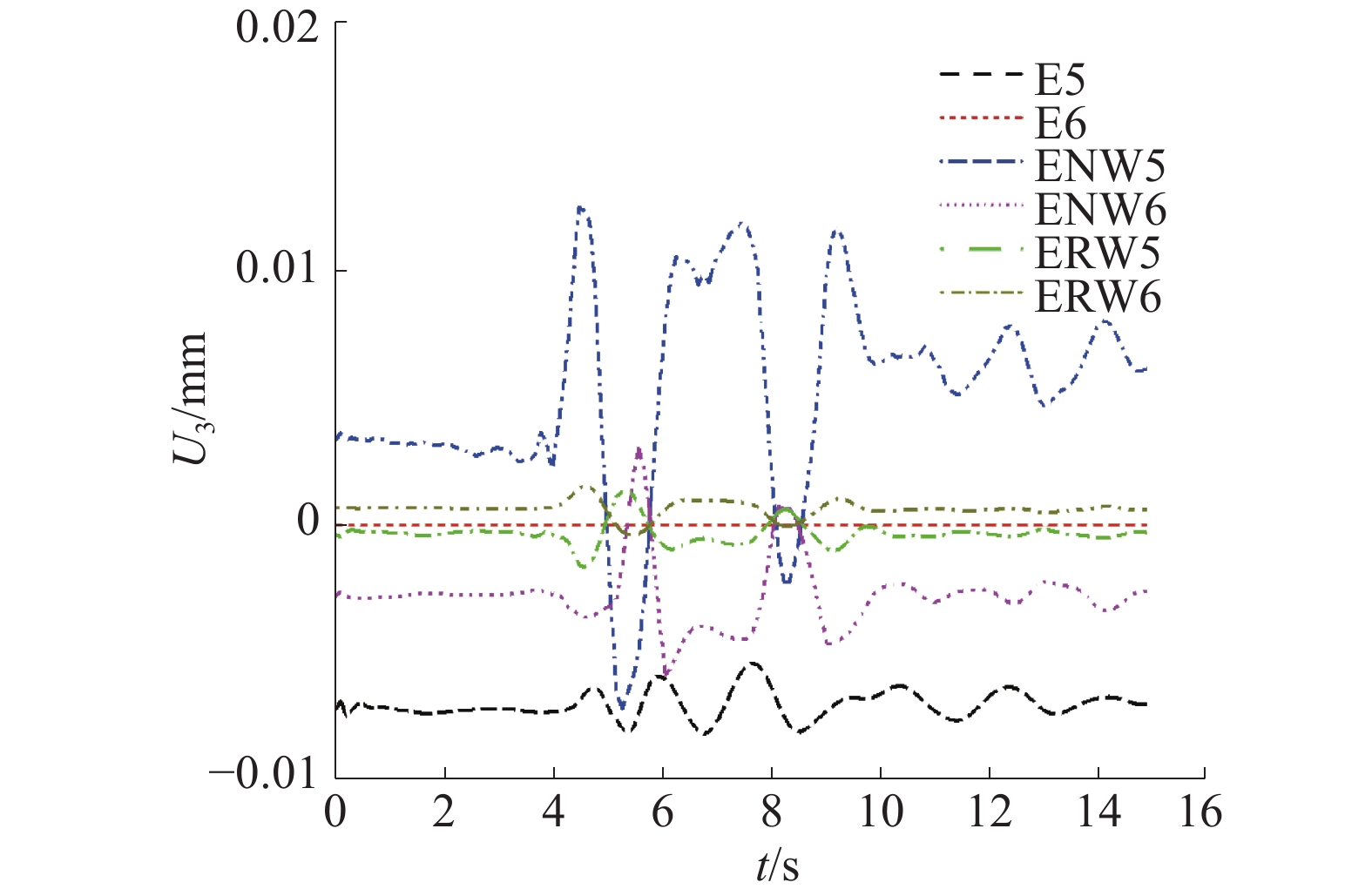
| 图 10 z方向5点和6点位移曲线 | |
从图5~10中可以看出,与单独地震作用相比,地震和波浪共同作用下面内水平x方向各关键点位移响应的变化基本一致,无明显差异;面内竖直y方向各关键点位移响应有一定差异;垂直于面内z方向各关键点位移响应很小,对于斜坡式防波堤这样的大型海洋结构而言,可忽略不计。所以,与单独地震作用相比,在地震和波浪共同作用下对斜坡式防波堤结构的竖向(y向)残余变形的影响显著。在水平方向(x向),斜坡式防波堤结构的残余变形只考虑地震荷载即可。
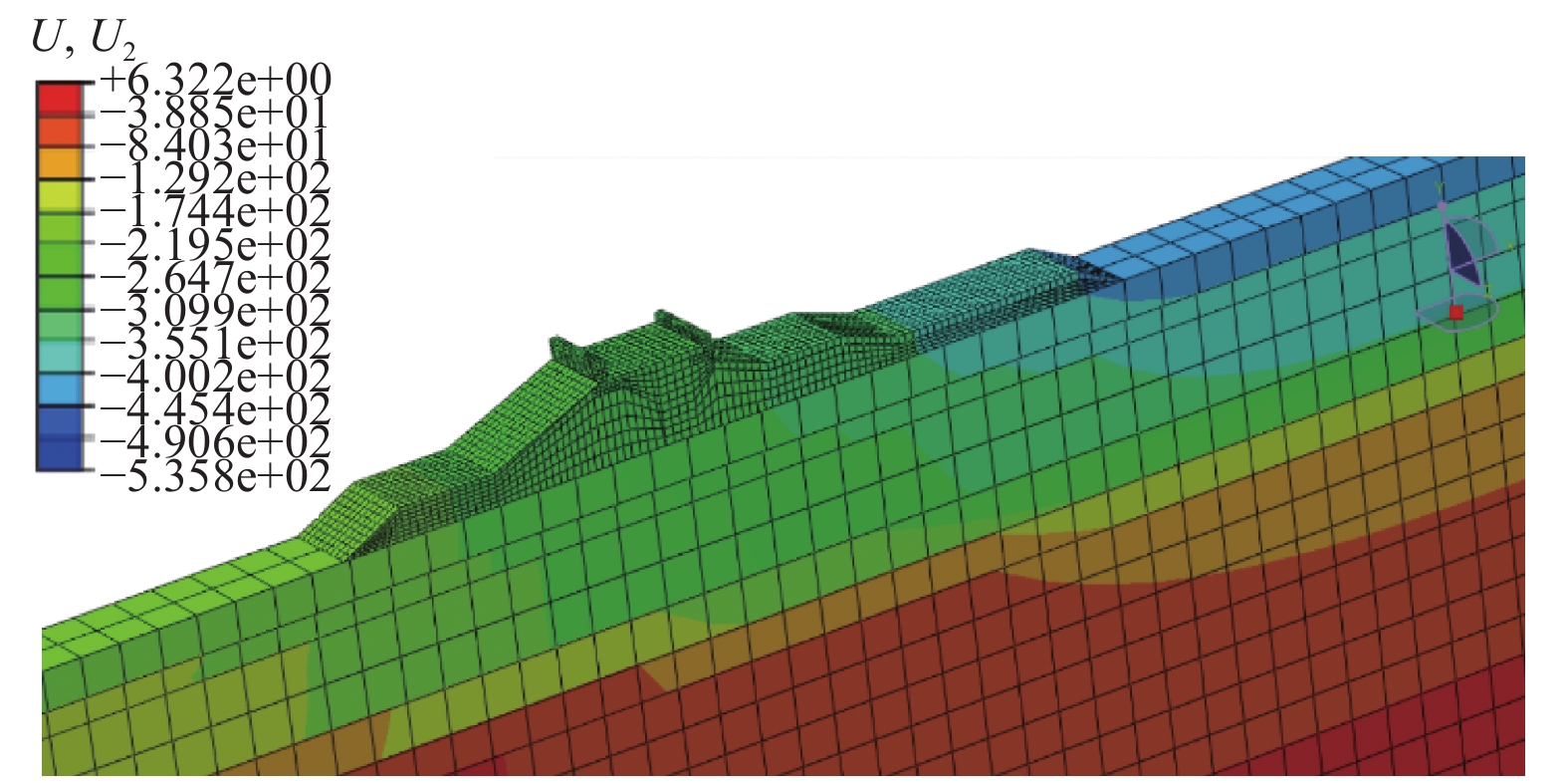
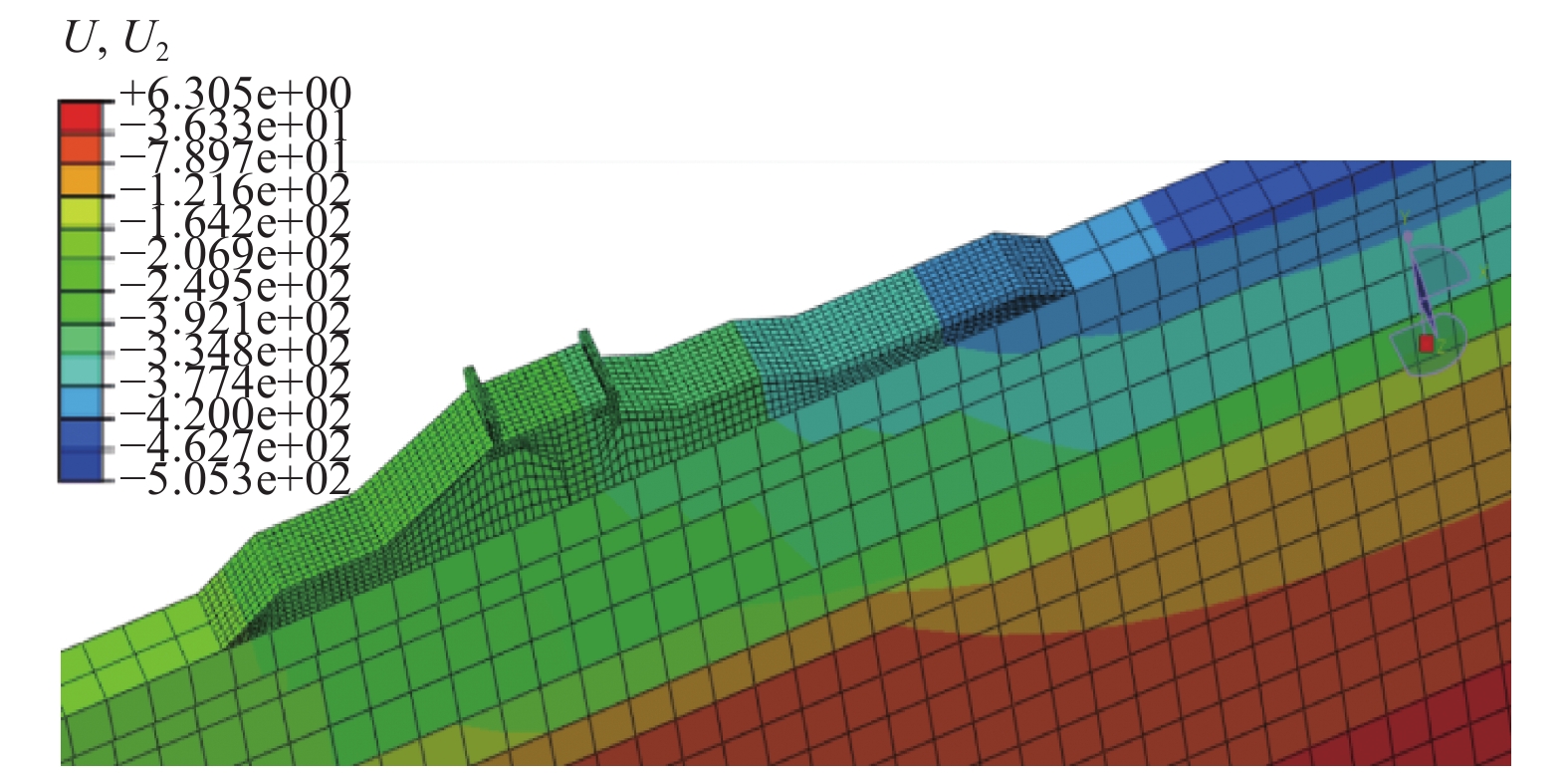
3.4 地震和波浪共同作用下斜坡式防波堤的竖向残余变形在上述斜坡式防波堤的动力响应分析的基础上,图11~13分别给出了在不同荷载作用下,斜坡式防波堤的竖向残余变形云图。在不同荷载作用下,斜坡式防波堤关键点的竖向残余变形如表3所示。
|
Download:
|
| 图 11 地震作用下竖向残余变形 | |
|
Download:
|
| 图 12 地震和总波浪力共同作用下竖向残余变形 | |

|
Download:
|
| 图 13 地震和规则波共同作用下竖向残余变形 | |
|
|
表 3 不同荷载作用下的竖向残余变形 |
从表3可以看出,前后挡浪墙在地震作用下的竖向残余变形均大于地震和波浪共同作用下的竖向残余变形;向海侧坡脚在地震作用下的竖向残余变形小于地震和波浪共同作用下的竖向残余变形;背海侧坡脚在地震作用下的竖向残余变形大于地震和波浪共同作用下的竖向残余变形。
4 结论本文利用ABAQUS有限元软件对斜坡式防波堤在地震、以及地震和波浪共同作用下的动力响应进行了仿真研究,得到如下结论:
1)在地震和波浪共同作用下,斜坡式防波堤残余变形机理十分复杂。向海侧坡脚在地震和波浪共同作用下的竖向残余变形大于单独地震作用下的竖向残余变形;而前后挡浪墙和背海侧坡脚在地震和波浪共同作用下的竖向残余变形均小于单独地震作用下的竖向残余变形。由此可见,地震发生时波浪的存在将对斜坡式防波堤结构竖向残余变形造成不同程度的影响。
2)波浪荷载分别按总波浪力和规则波的方式加载,但从竖向残余变形的仿真结果来看,两者的差别很小。
3)地震和波浪共同作用与单独地震作用相比,斜坡式防波堤结构的水平残余变形无明显差异,所以水平方向的残余变形只考虑地震荷载即可。
由于斜坡式防波堤的动力响应不仅取决于复杂的结构形式及边界条件,还取决于海洋结构、海水和地基三者的相互影响,准确把握其动态特性,还需要在理论和试验方面作进一步的深入研究。
| [1] |
杨勋, 王欢欢, 余克勤, 等. 流−固耦合作用下斜坡式防波堤地震动力响应分析[J]. 工程力学, 2016, 33(10): 248-256. ( 0) 0)
|
| [2] |
YE J H, JENG D S. Three-dimensional dynamic transient response of a poro-elastic unsaturated seabed and a rubble mound breakwater due to seismic loading[J]. Soil dynamics and earthquake engineering, 2013, 44: 14-26. DOI:10.1016/j.soildyn.2012.08.011 ( 0) 0)
|
| [3] |
YANG Xun, JIN Xianlong. Dynamic analysis of a rubble-mound breakwater subject to earthquake including seawater-structure-foundation interaction[J]. Proceedings of the institution of mechanical engineers, part M: journal of engineering for the maritime environment, 2015, 230(2): 310-326. ( 0) 0)
|
| [4] |
OKADA K, SUZUKI K, ARIKAWA T. Study of a force to act on a breakwater at the superposition of an earthquake and the tsunami[J]. Journal of Japan society of civil engineers Ser B2 (coastal engineering), 2016, 72(2): I_1057-I_1062. DOI:10.2208/kaigan.72.I_1057 ( 0) 0)
|
| [5] |
武崇福, 刘贝贝. 波浪和地震作用下高桩承台−土−结构动力响应[J]. 土木建筑与环境工程, 2011, 33(6): 7-12, 58. ( 0) 0)
|
| [6] |
何晓宇, 李宏男. 波浪与地震对小尺度桩柱的共同作用研究[J]. 地震工程与工程振动, 2007, 27(5): 139-145. DOI:10.3969/j.issn.1000-1301.2007.05.021 ( 0) 0)
|
| [7] |
李忠献, 黄信. 地震和波浪联合作用下深水桥梁的动力响应[J]. 土木工程学报, 2012, 45(11): 134-140. ( 0) 0)
|
| [8] |
柳国环, 练继建, 于通顺. 地震与波浪作用下近海风电结构响应及倒塌模式[J]. 应用基础与工程科学学报, 2016, 24(1): 71-80. ( 0) 0)
|
| [9] |
荣维栋, 李洪斌. 近海单桩风机在波浪地震联合作用下的动力特性分析[J]. 江苏科技大学学报(自然科学版), 2015, 29(1): 27-32. DOI:10.3969/j.issn.1673-4807.2015.01.005 ( 0) 0)
|
| [10] |
何晓宇, 李宏男. 地震与波浪联合作用下海洋平台动力特性分析[J]. 海洋工程, 2007, 25(3): 18-25. DOI:10.3969/j.issn.1005-9962.2007.03.006 ( 0) 0)
|
| [11] |
CHAUDHARY B, HAZARIKA H, ISHIBASHI I, et al. Sliding and overturning stability of breakwater under combined effect of earthquake and tsunami[J]. Ocean engineering, 2017, 136: 106-116. DOI:10.1016/j.oceaneng.2017.03.021 ( 0) 0)
|
| [12] |
柳春光, 张士博. 考虑地震、波浪和海流作用的跨海桥梁结构研究进展[J]. 大连理工大学学报, 2017, 57(1): 105-110. ( 0) 0)
|
| [13] |
居荣初, 曾心传. 弹性结构与液体的耦联振动理论[M]. 北京: 地震出版社, 1983.
( 0) 0)
|
| [14] |
沈靠山, 李翔. 秦山核电厂海堤加高工程挡浪墙波浪力研究[J]. 浙江水利科技, 2013, 41(3): 53-54. DOI:10.3969/j.issn.1008-701X.2013.03.019 ( 0) 0)
|
| [15] |
王艳. 基于ABAQUS的混凝土重力坝地震响应仿真分析[D]. 杨凌: 西北农林科技大学, 2010.
( 0) 0)
|
| [16] |
中国水电水利科学研究院. DL 5073-2000, 水工建筑物抗震设计规范[S]. 北京: 中国电力出版社, 2001.
( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


