2. 北京航空航天大学 中法工程师学院,北京 100191
2. Sino-French Engineer School, Beihang University, Beijing 100191, China
表面等离子体共振(SPR)是在金属和电介质界面处,入射光场在一定入射角(即最佳激发角)下引发金属表面的自由电子相干振荡的一种物理现象。当发生表面等离子体共振现象时,由于入射光产生的消逝波与等离子波产生共振,反射光的强度会大大减弱。因此在图像采集系统获得的后焦面图像上将产生对称的圆弧或完整的圆环(后文统称为吸收谱),当被检测金属材料的特性(例如厚度)发生变化时,激发表面等离子体共振所需的最佳激发角的大小会发生变化,后焦面图像上的吸收谱的半径也会对应发生变化。根据这一关系,通过检测吸收谱半径,可以对材料表面的细微变化进行高精度的实时检测。这种特性使得表面等离子体共振被广泛地应用于纳米材料、生物医学、环境检测等领域[1−2]。传统的表面等离子体共振激发系统是Kretschmann[3]提出的全反射棱镜耦合系统,该系统的空间分辨率有限。针对这一问题,Kano[4]提出了表面等离子体显微镜系统(surface plasmon microscopy,SPM),SPM系统应用高分辨率显微镜解决了全反射棱镜耦合系统空间分辨率较低的问题[5]。但由于缺乏高效且精确的自动化识别方法,SPM系统难以做成高效的自动化仪器[6]。现有研究主要集中于表面等离子体共振的激发方法,而识别方法的研究非常有限。所有表面等离子体系统中的最佳激发角识别问题均可转化为后焦面吸收谱识别问题。目前吸收谱识别方法主要是手动勾画或者基于通光孔径中心的一维径向灰度识别(下文称为一维识别)。手动勾画吸收谱需要人工介入,难以实现对大批量后焦面图像的高效识别;一维识别方法要求吸收谱与通光孔径严格共心,并基于该中心统计穿过吸收谱方向的灰度分布,灰度分布曲线上的极小值点对应吸收谱。在噪声背景下,分布曲线上可能出现噪声引起的极小值,会影响识别的准确性。因此在后焦面上存在大量噪声的情况下,难以对吸收谱进行精确地识别。为了提高识别准确性与识别效率,本文提出了基于霍夫变换、形态学以及最小二乘法的SPR后焦面吸收谱识别方法,可以在强噪声背景下精确地识别SPR吸收谱。
1 后焦面吸收谱识别方法研究表面等离子体共振后焦面图像如图1所示,亮色圆形光斑是后焦面上的通光孔径,表面等离子体共振吸收谱以通光孔径内部的两段暗色圆弧的方式呈现。特别地,后焦面图像呈现不均匀现象,图1中右侧亮度整体高于左侧,黑色背景和通光孔径内部包含大量斑点噪声。本文提出的基于形态学的SPR后焦面吸收谱识别方法,它的识别流程图如图2所示。

|
Download:
|
| 图 1 表面等离子体共振后焦面图像 | |
|
Download:
|
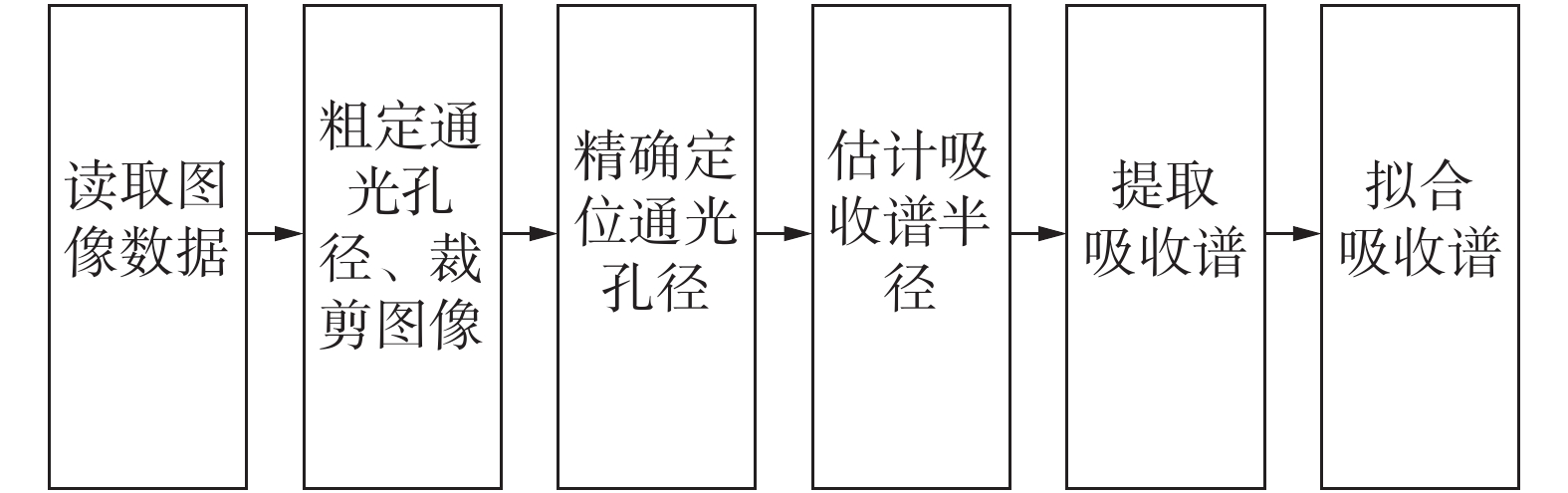
| 图 2 识别方法流程 | |
识别方法的基本流程是:1)读取表面等离子体后焦面图像;2)通过二值化提高通光孔径与背景对比度,接着应用霍夫变换粗略定位通光孔径,基于定位结果裁剪图像;3)采用更小分块的二值化,获得更精细的通光孔径轮廓,应用霍夫变换对通光孔径进行精确识别;4)基于通光孔径精确圆心,粗略估计吸收谱半径;5)应用形态学方法提取吸收谱圆弧;6)应用最小二乘法拟合吸收谱。
1.1 基于霍夫变换的图像裁剪表面等离子体后焦面图像通常为矩形,通光孔径不在图像中心,图像中存在着大量背景噪声,给图像识别带来了不利影响。可先裁剪后焦面图像,使得通光孔径位于图像中心,缩小图像尺寸,使得有效内容更加突出,也可减少后续识别过程中的运算量,加快了识别速度。为了粗略定位出通光孔径在原始图像中的位置,给裁剪提供参考,采用分块二值化和霍夫变换相结合的方法。
1.1.1 基于全局与局部阈值相结合的二值化后焦面图像数据亮度不均匀,左侧较暗、右侧较亮。为了使通光孔径的左右两侧均能较完整地区分于黑色背景,采用全局阈值与局部阈值相结合的二值化方法,将图像分成若干相同大小的子块,对每个子块计算子块的局部阈值
| $T{\rm{ = }}a{T_g} + b{T_l}$ | (1) |
分块二值化过程中,需要先确定图像分块的大小。不同的分块尺寸会使二值化的结果存在较大的差异,如果分块尺寸较大则图像细节较少;相反地,如果分块尺寸较小则保留更多的图像细节。应用分块二值化时根据实际需求合理选取图像分块大小。粗定通光孔径位置时,只需获得通光孔径的大致轮廓,可选择较大的分块尺寸。本文中,设置图像分块尺寸为150 pix×150 pix。选择图1中的样例图像,利用式(1)计算的阈值得到的二值化结果如图3所示。分块二值化方法解决了图像中通光孔径明暗不均匀的问题,为后续使用霍夫变换粗定位通光孔径打下基础。

|
Download:
|
| 图 3 后焦面图像二值化结果 | |
对图3所示的二值图像应用霍夫变换粗定位通光孔径前,采用半径为3 pix的圆盘形结构开运算,可以在不改变通光孔径轮廓大小的情况下,有效去除通光孔径外部的斑点噪声,减小噪声对霍夫变换的影响。提高霍夫变换识别准确性。
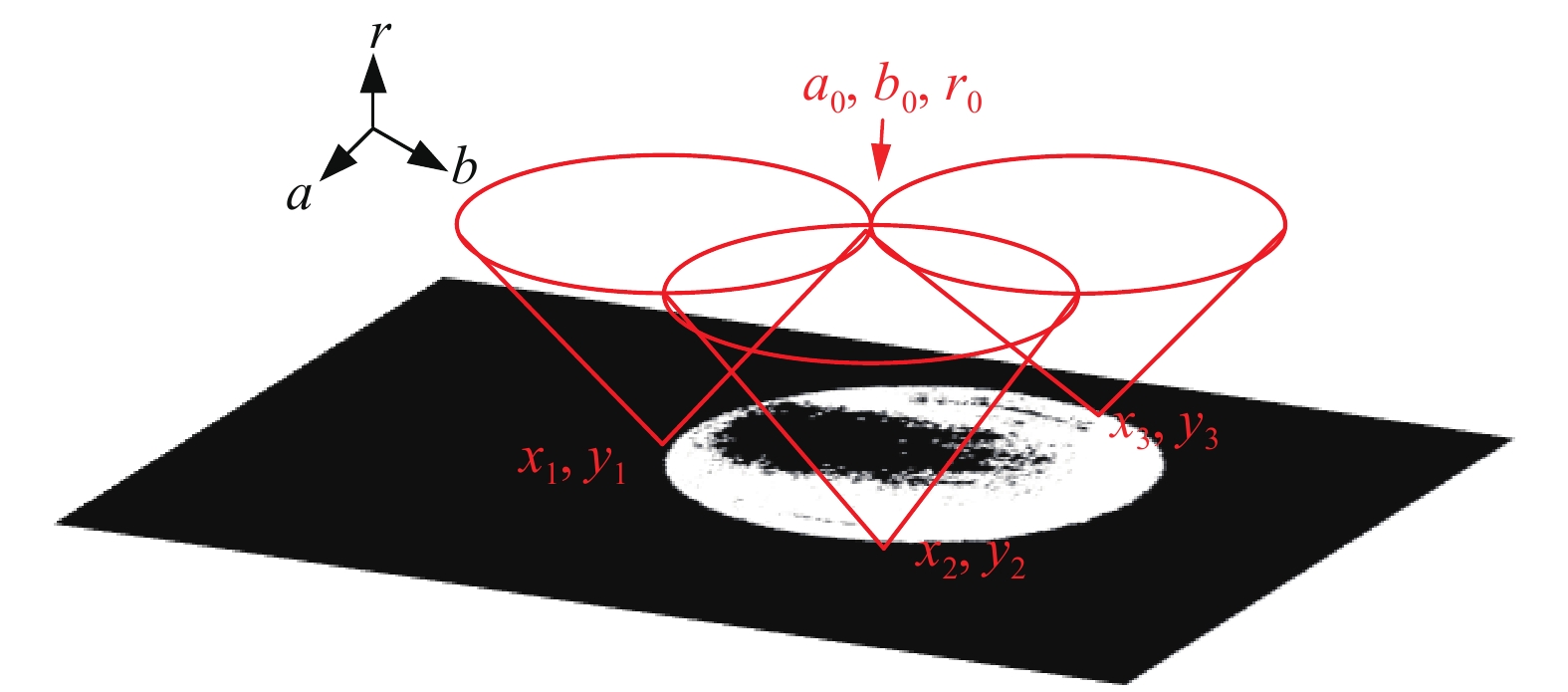
1.1.2 基于霍夫变换的通光孔径粗定位霍夫变换是图像处理中常用的几何形状检测方法[8−9],该方法的主要思想是将图像
|
Download:
|
| 图 4 霍夫变换圆检测原理 | |
通过霍夫变换识别到图3中,通光孔径圆心
|
Download:
|
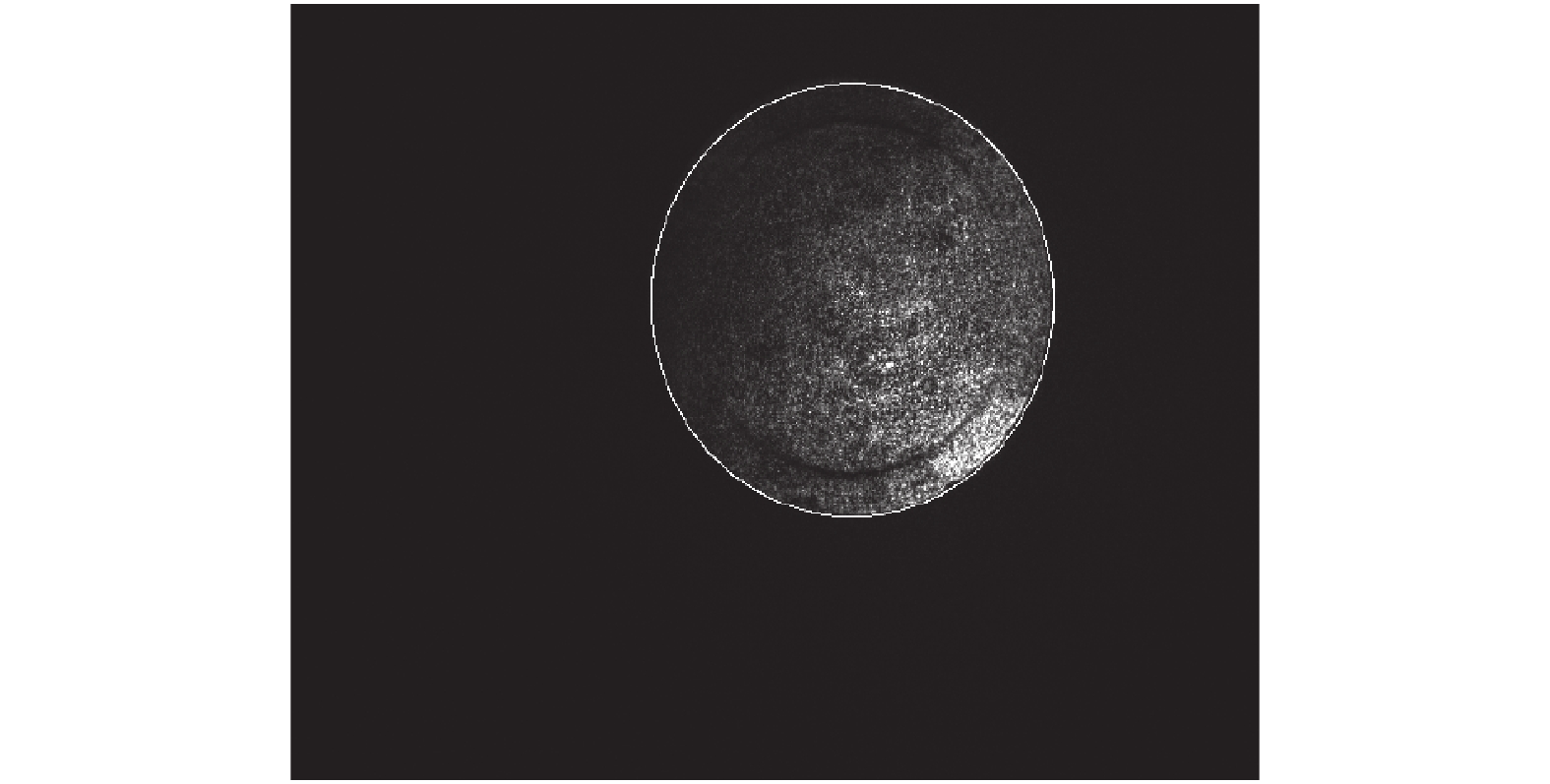
| 图 5 后焦面图像通光孔径粗定位结果 | |
依据1.1.2节中基于霍夫变换的粗定位结果,以粗定位圆心位置为中心裁剪图像。由于通光孔径粗定位结果与通光孔径真实位置存在细微差异,为了防止过度裁剪导致通光孔径信息丢失,在裁剪图像时需要保留一定裕量。在本文中所有SPR测试图像均保留80 pix的裕量。由于后焦面通光孔径为圆形,因此可以设定裁剪后图像的边长为
|
Download:
|
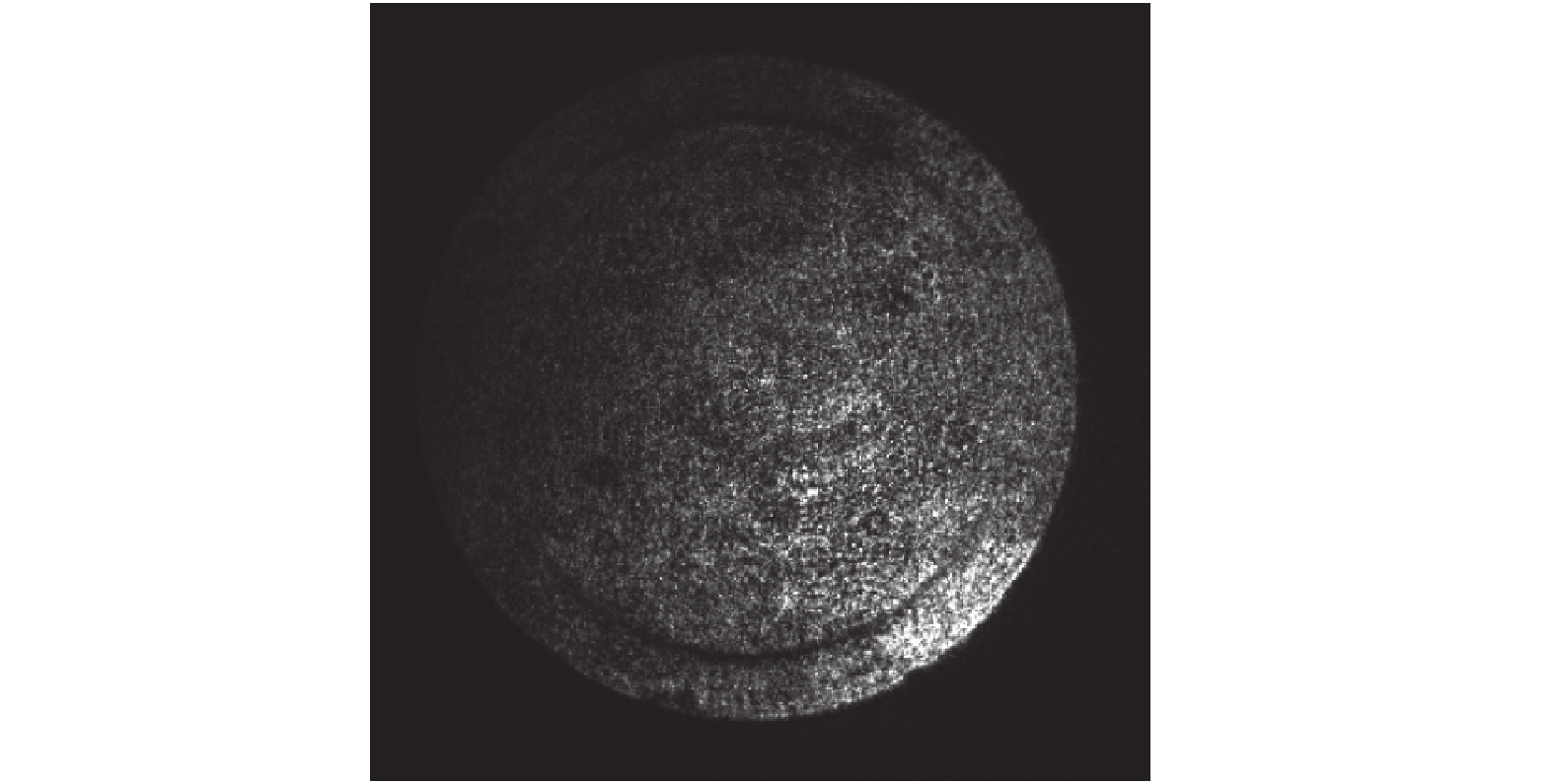
| 图 6 裁剪后的后焦面图像 | |
为了获得通光孔径精确定位结果,需要二值图像中的通光孔经轮廓清晰且完整。因此在分块二值化过程中选择稍小的分块,获得更多的通光孔径边界细节信息。可以基于图像尺寸设置分块大小。假设图像的宽度为

|
Download:
|
| 图 7 裁剪后的图像 | |
在图7(a)所示的二值图像中,可以观察到位于图像竖直方向的两段吸收谱。从二值图像中分离出吸收谱,利用最小二乘法拟合曲线,可得到吸收谱的参数。
1.3.1 吸收谱半径粗略估计为了从如图7(a)所示的二值图像中分离出吸收谱,需要自动地判断圆弧在图像中的位置。基于吸收谱与通光孔径共心的理论前提,可假设两者同心。但考虑到实际测量中微弱偏心的可能,此假设仅用于粗略估计吸收谱半径,可以为消除吸收谱内外噪声做参考。基于利用霍夫变换精确识别的通光孔径中心

|
Download:
|
| 图 8 径向灰度分布曲线 | |
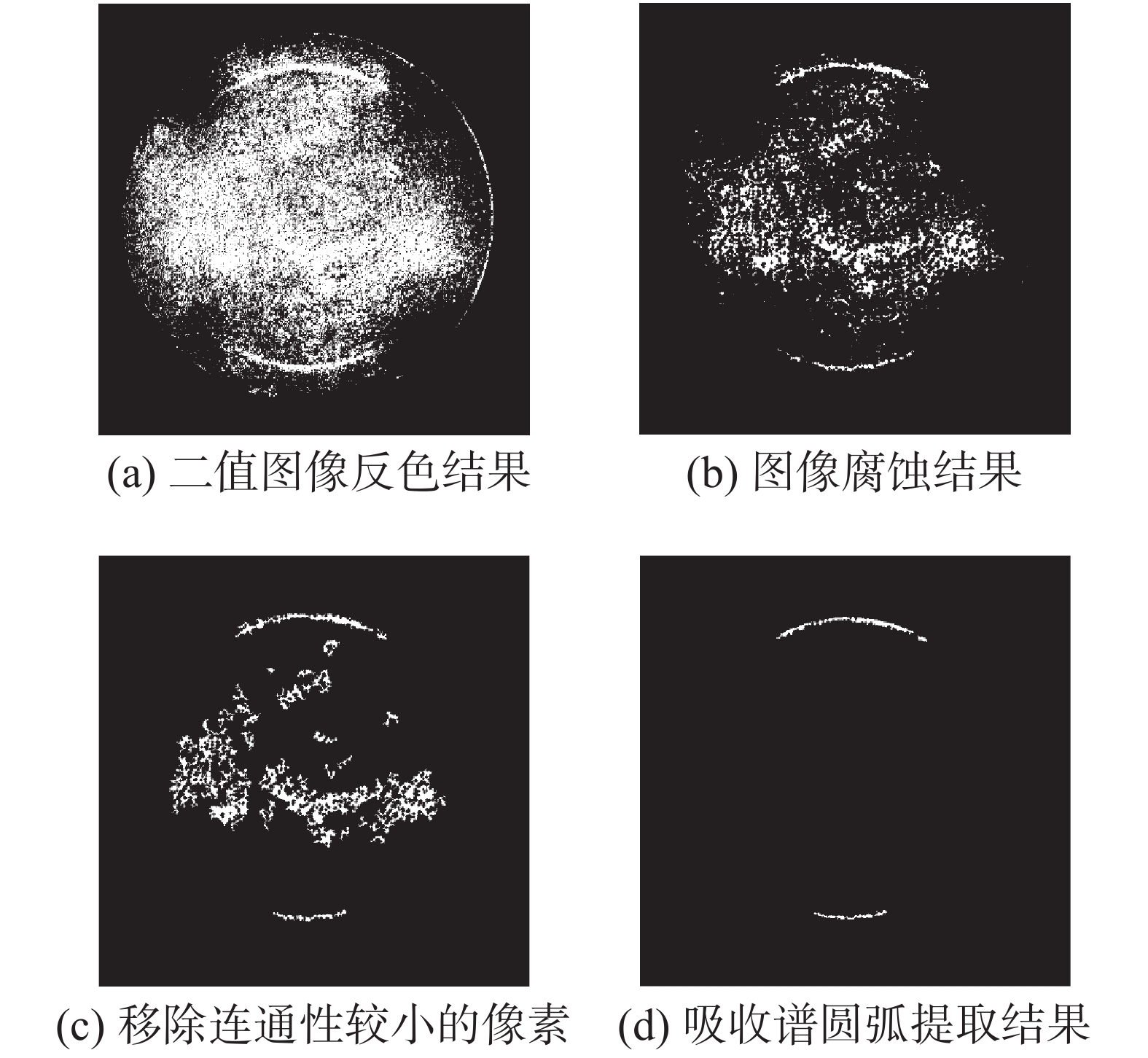
为了利用最小二乘法精确地拟合吸收谱,需要提取后焦面图像吸收谱,即将所有无关信息去除,仅保留吸收谱信息。吸收谱的提取涉及形态学腐蚀和像素连通性判断,主要包含以下步骤:1)观察图7(a)可以发现,吸收谱在二值图像中表现为背景(黑色)。为了提取吸收谱,需将吸收谱转换为前景(白色),即将图7(a)的二值化结果反色,并把通光孔径外部像素置零,如图9(a)所示;2)设置形态结构元素,对步骤1)的结果应用半径为2的圆盘形的形态学腐蚀,得到的结果如图9(b)所示;3)移除步骤2)的结果中连通性小于P的像素点,选择P的取值时,应保证与吸收谱无关的区域被尽可能多地移除。此次试验均设置P=50,得到的结果如图9(c)所示;4)假设吸收谱与通光孔径同心,基于1.3.1节的吸收谱半径粗估计结果
|
Download:
|
| 图 9 后焦面图像吸收谱提取过程 | |
基于利用形态学方法获得的图9(d)的吸收谱圆弧提取结果,可以近似地得到后焦面图像中吸收谱上点的坐标。建立圆形模型,基于吸收谱提取结果,利用最小二乘法拟合圆,即可以得到吸收谱的参数。
设圆心为
将图9所示的吸收谱图像中的
| $\left[ {\begin{array}{*{20}{l}} {2{x_1}}&{2{y_1}}&1 \\ {2{x_2}}&{2{y_2}}&1 \\ \vdots & \cdots & \vdots \\ {2{x_n}}&{2{y_n}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{c_1}} \\ {{c_2}} \\ {{c_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {x_1^2 + y_1^2} \\ {x_2^2 + y_2^2} \\ \vdots \\ {x_n^2 + y_n^2} \end{array}} \right]$ | (2) |
式(2)可以表示为
| $ {{X}} = ({{{A}}^{\rm{T}}}{{A}}){{{X}}^{\rm{T}}}{{b}} $ |
进而可以计算出吸收谱的圆心
通过上述最小二乘方法拟合出的吸收谱如图10所示,得到吸收谱圆心

|
Download:
|
| 图 10 吸收谱与通光孔径识别结果 | |
为了验证本文提出方法的通用性,将所提方法应用于其他的测试图像,包含线性偏振激发的后焦面图像(测试图像1)和径向偏振激发的后焦面图像(测试图2~4)。得到的圆心和半径的识别结果如表1所示。图11给出了经过算法裁剪的不同测试图像及对应的吸收谱与通光孔径检测结果。
|
|
表 1 不同测试图像的通光孔径与吸收谱参数 |

|
Download:
|
| 图 11 不同测试图像及识别结果 | |
通过图11给出的测试图像的识别结果,可以发现,本文提出的识别方法对于径向偏振以及线性偏振激发的表面等离子体后焦面吸收谱有较好的识别效果,且吸收谱的圆心与通光孔径圆心相差很小,最大偏差限定在在2 pix以内。吸收谱与通光孔径存在偏心现象是由于搭建的表面等离子体激发系统的准直性不足,本文提出的识别方法能够检测吸收谱与通光孔径的偏心状况,作为激发系统校正的参考。
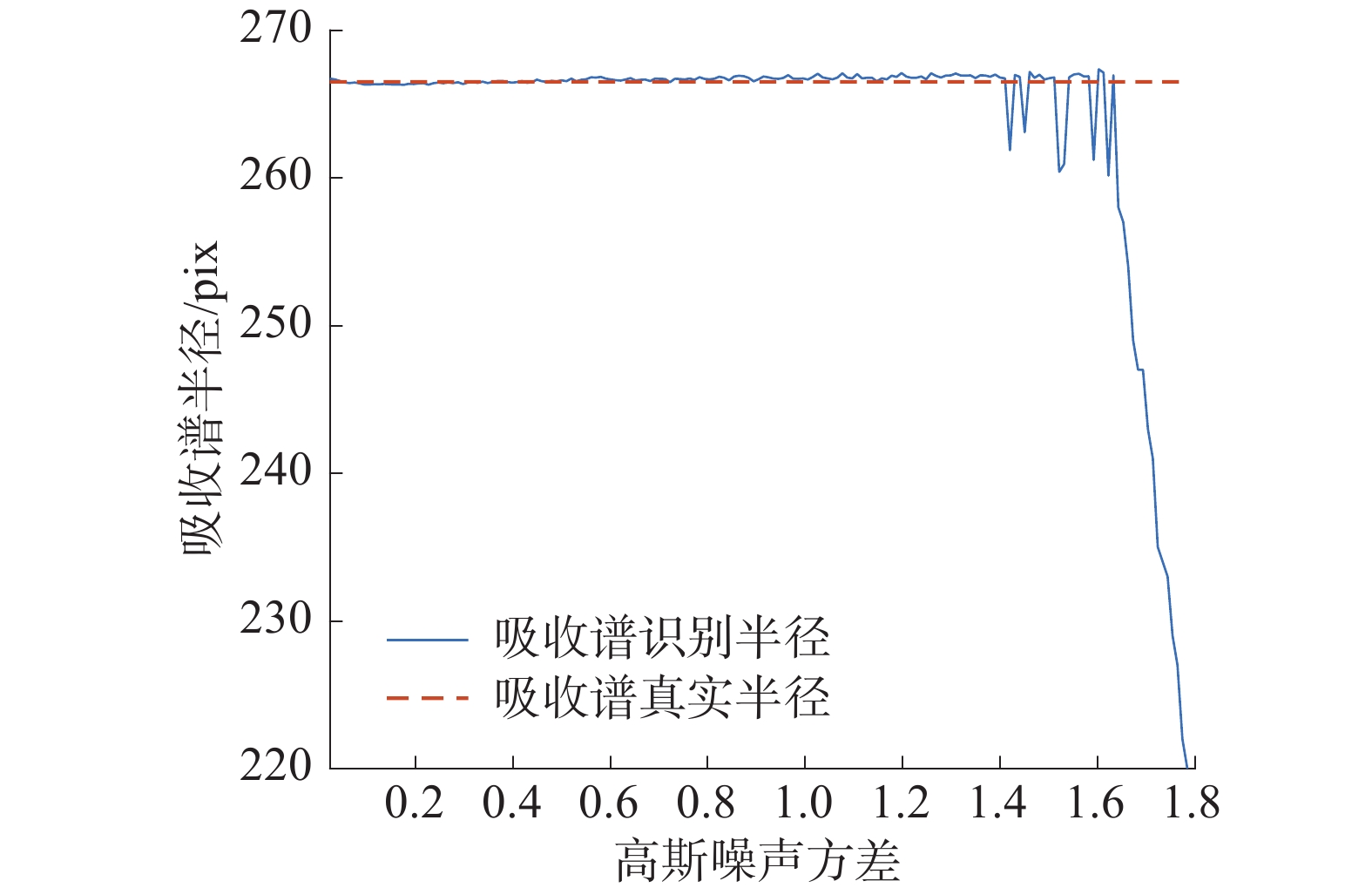
为了验证本文提出的识别方法在强噪声背景下的鲁棒性,在基于无噪声的表面等离子体共振后焦面仿真图像中,添加不同方差的高斯噪声,模拟不同噪声强度下的后焦面图像,并使用本文提出的方法识别噪声背景下的吸收谱。比较不同强度噪声下的吸收谱识别结果与仿真图像中真实的吸收谱半径,可以得到如图12所示的结果。通过图12可以发现,提出的吸收谱识别方法在高斯噪声的方差介于0~1.3时,表现出很强的鲁棒性,识别的吸收谱半径与真实吸收谱半径相差在1像素以内。而方差为1.3的高斯噪声强度大于现有SPM系统的噪声强度,因此本文提出的吸收谱识别方法的在强噪声背景下的鲁棒性足以满足现有SPM系统的需求。
|
Download:
|
| 图 12 不同强度高斯噪声下的识别结果 | |
本文针对表面等离子体后焦面中吸收谱识别困难的问题,提出了基于霍夫变换、形态学降噪与最小二乘法相结合的后焦面吸收谱识别方法,它用于解决不同激发方式下的表面等离子体共振后焦面吸收谱识别问题。相比于传统的识别技术,本文提出的识别方法对于噪声有较好的鲁棒性,它为表面等离子体识别仪器的开发提供了高效、精确的识别技术。本文的后续研究工作主要包括:1)研究优化识别的优化问题,它将使识别过程不依赖于通光孔径与吸收谱共心的基本假设;2)提高识别方法的自动化程度,它将最大限度地减少识别过程中的人工干预过程。
| [1] |
施玉佳, 王凯. 表面等离子体共振生物传感器综述[J]. 新丝路, 2016(12): 217. ( 0) 0)
|
| [2] |
刘小桃. 表面等离子体共振技术在环境污染物监测中的应用研究[J]. 低碳世界, 2016(9): 19-20. ( 0) 0)
|
| [3] |
KRETSCHMANN E, RAETHER H. Radiative decay of non radiative surface plasmons excited by light[J]. Zeitschrift für naturforschung A, 1968, 23(12): 2135-2136. ( 0) 0)
|
| [4] |
KANO H. Excitation of surface plasmon polaritons by a focused laser beam[M]// KAWATA S. Near-Field Optics and Surface Plasmon Polaritons. Berlin, Heidelberg: Springer, 2001: 189-206.
( 0) 0)
|
| [5] |
王毅, 胡永奇, 张庆文. 一种基于表面等离子体共振的光学显微镜[P]. 中国: CN105628655A, 2016-06-01.
( 0) 0)
|
| [6] |
SOMEKH M G, STABLER G, LIU Shugang, et al. Wide-field high-resolution surface-plasmon interference microscopy[J]. Optics letters, 2009, 34(20): 3110-3112. DOI:10.1364/OL.34.003110 ( 0) 0)
|
| [7] |
龙建武, 申铉京, 陈海鹏. 自适应最小误差阈值分割算法[J]. 自动化学报, 2012, 38(7): 1134-1144. ( 0) 0)
|
| [8] |
DUDA R O, HART P E. Use of the Hough transformation to detect lines and curves in pictures[J]. Communications of the ACM, 1972, 15(1): 11-15. DOI:10.1145/361237.361242 ( 0) 0)
|
| [9] |
ILLINGWORTH J, KITTLER J. A survey of the Hough transform[J]. Computer vision, graphics, and image processing, 1988, 44(1): 87-116. DOI:10.1016/S0734-189X(88)80033-1 ( 0) 0)
|
| [10] |
屈汉章, 王洋, 吴成茂. 基于直径累积的霍夫变换检测圆算法[J]. 西安邮电大学学报, 2017, 22(5): 89-93. ( 0) 0)
|
| [11] |
HINTON E, CAMPBELL J S. Local and global smoothing of discontinuous finite element functions using a least squares method[J]. International journal for numerical methods in engineering, 1974, 8(3): 461-480. DOI:10.1002/(ISSN)1097-0207 ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


