随着信息技术的快速发展以及大数据时代的到来, 在给人们的生活和工作带来便利的同时, 也充斥着大量冗余信息。现实生活中, 用户经常会对购买的商品进行评分, 商家也会根据用户的评分情况对商品或服务做出相应的调整, 从而形成一个交互。系统得到用户对商品的评分后, 会生成1个评分矩阵, 然后根据用户对商品的评分情况进行处理, 分析用户的潜在特征, 从而为用户推荐其真正感兴趣的商品。如何从信息的汪洋里, 过滤用户真正需要的信息, 这是一个急需解决的问题^[1]。推荐系统可以根据用户已有的少量的记录为用户推荐其感兴趣的事物, 定位用户的个人喜好^[2]。本文中的推荐算法是在非负矩阵的基础上进行的, 目前非负矩阵分解已经应用于很多领域, 如机器学习、模式识别、文本挖掘、多媒体数据的分析等^[3]。

推荐系统的目的是将用户及其偏好的数据转化为对用户未来可能的喜好和兴趣进行预测。推荐系统主要基于3种实体基础, 即用户、条目(如电影、新闻等)和用户的历史记录(如分数、评论等)。推荐系统的主要任务是从用户的使用历史中找出描述用户和项目之间联系的有用模式, 然后根据这些模式对用户可能感兴趣的模式进行预测。其中1个很有名的就是协同过滤。用户项目评分矩阵通常都是基本数据源, 其中的每个条目都要根据相应的用户项目的历史记录进行建模, 且数值越高, 代表用户的偏好越强。由于每个用户只有1个项目集, 因此该评分矩阵通常会很稀疏, 会造成大量的缺失值^[4]。传统的采样方法如随机采样、均匀采样等^[5], 传统的推荐系统对于如何最佳的度量用户的相似性以及评估其不确定性有困难^[6]。

本文研究的问题是从大量的用户对电影的评分矩阵中进行分析, 找出用户的潜在特征, 并对其感兴趣的电影进行推荐。

1 相关工作

推荐系统是根据用户的已有记录, 通过分析其潜在特征, 对其感兴趣的电影进行推荐^[7], 但是由于用户对电影评分矩阵的稀疏性, 就需要对评分矩阵进行采样后近似^[8], 使得采样后的矩阵与原始矩阵相比误差尽可能小, 但是还要保留原始矩阵的特性。对采样后的矩阵进行分解^[9], 得出用户的特征。根据用户的特征以及各特征的比重, 可以对用户进行聚类, 将相似的用户归为1簇^[10], 也可以对用户感兴趣的电影进行推荐。

1.1 不完全矩阵的恢复

本文中是关于用户对电影的评分矩阵A, 其中每1行对应1个用户, 每1列对应1部电影。因此, ij^th表示的是第i个用户对第j部电影的评分。假设电影评分的有效等级为[-a, a]。矩阵A是1个秩为r的矩阵, 存在1个矩阵分解为A = UV^T, 其中, 矩阵A∈ $\mathbb{R}$^m×n, U∈ $\mathbb{R}$^m×r, V∈$\mathbb{R}$^n×r。一般的, m«n, 其中, m表示观众的数目, n表示电影的数目。毕竟每个观众观看的电影的数目是有限的, 而由于电影的种类很多, 导致其数目也很多, 因此, 每个观众不可能看完所有的电影。协同过滤是将可能被噪声或者被破坏的部分条目中恢复原来的矩阵, 因此, 可以根据用户对电影评分的有限的数据中恢复矩阵。也就是说, 对于(ij)∈Ω采样集${{\mathit{\boldsymbol{\hat A}}}_{ij}}, \mathit{\boldsymbol{\hat A}}{\rm{ = }}\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{E}}$是损坏的Y的副本^[11], 因此, 要想恢复A, 就要遵从如下优化:

$ \mathop {\min }\limits_{\mathit{\boldsymbol{U}},\mathit{\boldsymbol{V}}} \frac{1}{2}\left\| {{P_\mathit{\Omega }}\left( {\mathit{\boldsymbol{U}}{\mathit{\boldsymbol{V}}^{\rm{T}}} - \hat A} \right)} \right\|_F^2{\rm{s}}.{\rm{t}}.\;\;{\left\| {\mathit{\boldsymbol{U}}{\mathit{\boldsymbol{V}}^{\rm{T}}}} \right\|_{ij}} \le a $

(1)

式中P_Ω是抽样算子, 定义为

$ {\left[ {{P_\mathit{\Omega }}\left( A \right)} \right]_{ij}} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {A_{ij}},\\ 0, \end{array}&\begin{array}{l} \left( {i,j} \right) \in \mathit{\Omega }\\ \left( {i,j} \right) \notin \mathit{\Omega } \end{array} \end{array}} \right. $

因此, 最优解为A^*=U^*V^*T, 误差则表示为△=A-A^*。

1.2 个用户的预测错误

可以用式(2)分析基于矩阵分解恢复子空间的方法来预测新用户a_i^*∈N^gnd的评分, 其中N示的是r维度子空间。可以根据式(2)逐列估计整个矩阵:

$ a_i^ * = \mathit{\boldsymbol{N}}{\left( {\mathit{\boldsymbol{N}}_i^{\rm{T}}{\mathit{\boldsymbol{N}}_i}} \right)^{ - 1}}\mathit{\boldsymbol{N}}_i^{\rm{T}}{y_i} = {\mathit{\boldsymbol{N}}_{{\rm{pin}}}}v\left( {{N_{\rm{i}}}} \right){y_i} $

(2)

式中a_i^*表示恢复的完整的r秩矩阵A^*的第i列。

1.3 稳定性

当采样的数目足够多时, 对于噪声中分解方法的全局最优解是稳定的, 通过均方根误差来衡量:

$ {\rm{RMSE}} = \frac{1}{{mn}}\left\| {{A^ * } - A} \right\| $

定理1 存在1个常数M, 使得概率至少为1-2exp(-n)。

$ {\rm{RMSE}} \le \frac{1}{{\sqrt {\left| \mathit{\Omega } \right|} }}{\left\| {{P_\mathit{\Omega }}\left( E \right)} \right\|_F} + \frac{{{{\left\| E \right\|}_F}}}{{\sqrt {mn} }} + Mk{\left( {\frac{{nr{\rm{lon}}\left( n \right)}}{{\left| \mathit{\Omega } \right|}}} \right)^{\frac{1}{4}}} $

式中当|Ω|»nrlog(n), 最后1项减少, 且RMSE基本上受制于E的平均值, 即分解方法稳定。

1.4 改进的NMF

半NMF放松了对NMF的非负约束条件^[12], 使得矩阵X和矩阵F可以有混合符号, 只限制数据因子矩阵U, 使得该矩阵包含严格的非负分量:

$ \mathop {\min }\limits_{\mathit{\boldsymbol{U}},\mathit{\boldsymbol{F}}} {\left\| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{UF}}} \right\|^2}{\rm{s}}.{\rm{t}}.\mathit{\boldsymbol{U}} \ge 0 $

这是从聚类角度出发, 若将F看做聚类中心, 矩阵U就看做是每个数据点的聚类指示器。半NMF对其特征矩阵不要求施加正交性要求, 可以看成是一种软聚类方法^[13]。

半NMF-PCA聚类被定义为以下标准的最小化问题:

$ \mathop {\min }\limits_{\mathit{\boldsymbol{C}},W,C} {\left\| {\mathit{\boldsymbol{B}} - \mathit{\boldsymbol{CW}}{\mathit{\boldsymbol{C}}^{\rm{T}}}} \right\|^2}{\rm{s}}.{\rm{t}}.\mathit{\boldsymbol{C}} \ge 0,{\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{F}} = I $

式中‖ · ‖表示F范数。

C= (c_ij)表示大小为n×c的矩阵, 矩阵W = w_ij)是1个列的标准正交大小为c× c矩阵。而矩阵Q的计算通过公式得到

$ \min {\left\| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{C}}^{\rm{T}}}} \right\|^2} $

(3)

式中H =CW。

2 NystrÖm方法

NystrÖm方法最初是用来解决近似积分特征函数的问题^[14], 随着技术的进步, 被用来处理低阶近似的核心矩阵^[15]。假设给定任意1个核功能k(·, ·)以及样本集p(·), NystrÖm方法可以表示为

$ \int {k\left( {x,y} \right)p\left( y \right)\varphi \left( y \right)dy} = {\lambda _i}{\varphi _i}\left( x \right) $

式中φi(x)、λ_i 分别是第i个特征值函数和关于p的k(·, ·)算子的特征值^[7]。假设输入1个对称的半正定核矩阵K∈ $\mathbb{R}$^n×n, 半正定矩阵是通过采样得到的具有标志性的点组成的矩阵^[16]。“标志点”选取的方法有很多, 其中最常见的是无替代的均匀采样^[17]。若矩阵的秩rank(K= r ≤ n, 即存在1个L∈ $\mathbb{R}$ ^n×n, 使得K= L^TL。文中将从原始的观众对电影的评分矩阵A中利用距离公式, 得到用户和用户或者观众和观众的相似度矩阵B, 由于矩阵的规模较大, 因此, 采取适当的列c « n组成矩阵B的近似矩阵${\mathit{\boldsymbol{\tilde B}}}$。假设采样的列数为c, 采样后的矩阵C的大小为n×c, 内部矩阵W的大小为c×c。由于矩阵B对称半正定的特性^[18], 因此, 矩阵W也是对称半正定矩阵。一般的, 矩阵B和C可以表示为

$ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{W}}&{\mathit{\boldsymbol{B}}_{21}^{\rm{T}}}\\ {{\mathit{\boldsymbol{B}}_{21}}}&{{\mathit{\boldsymbol{B}}_{22}}} \end{array}} \right] $

$ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{W}}\\ {{\mathit{\boldsymbol{B}}_{21}}} \end{array}} \right] $

式中:矩阵W是1个大小为c ×c的矩阵, 矩阵B₂₁的大小为(n-c)×c, 矩阵B₂₂是1个大小为(n-c)×(n-c)的矩阵。

假设采样后矩阵B的k秩近似矩阵${\mathit{\boldsymbol{\tilde B}}}$, 且c < n, 因此可以定义为

$ \mathit{\boldsymbol{\tilde B}} = \mathit{\boldsymbol{\tilde B}}_k^{{\rm{nys}}}{\left( {\tilde \Sigma _k^{{nys}}} \right)^{\rm{T}}} = \mathit{\boldsymbol{CW}}_k^ + {\mathit{\boldsymbol{C}}^{\rm{T}}} \approx \mathit{\boldsymbol{B}} $

用W_k表示符合矩阵W的谱范数或F范数的最佳k秩近似, W_k⁺则表示矩阵W_k的伪逆^[17]。可以看到, 当k =c时, B的标准NystrÖm近似就可以写为

$ \mathit{\boldsymbol{\tilde B}}_c^{{nys}} = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{W}}^ + }{\mathit{\boldsymbol{C}}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{W}}&{\mathit{\boldsymbol{B}}_{21}^{\rm{T}}}\\ {{\mathit{\boldsymbol{B}}_{21}}}&{{K_{21}}{W^ + }{\mathit{\boldsymbol{B}}_{22}}} \end{array}} \right] $

使用的标准NystrÖm方法得到的B的近似为CW_k⁺C^{T [19]}。

3 推荐系统 3.1 降维空间中的邻域形成

在基于矩阵分解的推荐系统中, 历史用户行为通常是为用户评分项目进行建模, 有如下定义。

定义1 假设给定1个项目集合I和用户的集合U, 因此用户对项目的评分矩阵A是1个|U|×|I的矩阵, 其中的每个元素a_{u, i}表示用户u与项目i评分成正比。因此, 推荐系统可以看成是估计丢失数据的1个过程。

定义2 矩阵A_K和矩阵A_W分别表示集合A中的已知的和整个的项目。给定T∈A_K表示训练集, 近似的目的是构建1个矩阵B来产生预测的项目${{\tilde b}_{u, i}}$, 对于每一个(u, i)∈A_W使得

$ \min \left( {\sum\limits_{\left( {u,i} \right) \in {A_W}} {\left| {{a_{u,i}} - {b_{u,i}}} \right|} } \right) $

类似于其他的协同过滤, 非负矩阵分解也将原始的评分矩阵A分为2个秩为f的矩阵P和Q, 其中矩阵P表示为|U|×f, 矩阵Q则表示为|I×f并且f «min(|U|, |I|)。注意到, 矩阵P和Q表示的是用户和电影的特征矩阵, 这反映了评分中包含的用户和定影的特征数据。这个分解过程是通过最小化测量矩阵A和f秩估计矩阵P之间的差异成本函数来实现的, 如欧几里得距离或者Kullback-Leibler差异^[20-21]。但是, NMF按照这种分解会受到非负条件的约束, 如要求P, Q ≥ 0。因此, 随着欧几里得距离的损失函数, 基于NMF的本文的推荐系统可以归为

$ \mathop {{\rm{argmin}}}\limits_{P,Q} {{\rm{d}}_{A \to PQ}} = {\left\| {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{PQ}}} \right\|^2} $

其中的约束条件为P, Q ≥ 0。这种优化问题在实践中往往难以解决^[22], 但是NMF可以通过巧妙的操纵学习率来解决这个问题。首先, 没有非负性的限制, 式(3)的问题可以通过常规算法来解决。如随着梯度下降, 可以通过以下过程获得每个期望的参数:

$ {p_{u,k}} \leftarrow {p_{u,k}} + {\eta _{u,k}}\left( {{{\left( {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{Q}}^{\rm{T}}}} \right)}_{u,k}} - {{\left( {\mathit{\boldsymbol{PQ}}{\mathit{\boldsymbol{Q}}^{\rm{T}}}} \right)}_{u,k}}} \right) $

(4)

$ {q_{k,i}} \leftarrow {q_{k,i}} + {\eta _{k,i}}\left( {{{\left( {{\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)}_{k,i}} - {{\left( {{\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{QQ}}} \right)}_{k,i}}} \right) $

(5)

式中:p_{u, k}表示矩阵P中的第u行第k列; q_{k, i}表示矩阵Q中的第k行第i列, 这2个参数实际上分别表示了用户u的第k个特征和电影i的第k个特征; η_{u, k}和η_{k, i}则表示相应的学习率。给定最初的非负p_{u, k}和q_{k, i}, 由于式(4)和式(5)中的成分, 在训练过程中, 可能会失去非负性。为了保持矩阵P和Q的非负性, NMF对角操控学习效率如下:

$ {\eta _{u,k}} = \frac{{{p_{u,k}}}}{{{{\left( {PQ{Q^{\rm{T}}}} \right)}_{u,k}}}} $

(6)

$ {\eta _{k,i}} = \frac{{{q_{k.i}}}}{{{{\left( {{P^{\rm{T}}}PQ} \right)}_{k.i}}}} $

(7)

有了这种转变, 式(6)和(7)中的负成分被初始化的p_{u, k}和q_{k, i}消掉, 因此, 学习效率被重新定义为

$ {p_{u,k}} \leftarrow {p_{u,k}}\frac{{{{\left( {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{Q}}^{\rm{T}}}} \right)}_{u,k}}}}{{{{\left( {\mathit{\boldsymbol{PQ}}{\mathit{\boldsymbol{Q}}^{\rm{T}}}} \right)}_{u,k}}}} $

(8)

$ {q_{k,i}} \leftarrow {q_{k,i}}\frac{{{{\left( {{\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)}_{k,i}}}}{{{{\left( {{\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{PQ}}} \right)}_{k.i}}}} $

(9)

式中训练过程最终将趋于一致。非负训练过程只是NMF中必不可少的一部分。在CF中, 评分矩阵A通常是稀疏的且有大量的未知条目。因此, 式(8)和(9)中的规则应该被相应地更改为权重NMF(WNMF), 新的更新规则为

$ {p_{u,k}} \leftarrow {p_{u,k}}\frac{{{{\left( {\left( {{\mathit{\boldsymbol{W}}_ \circ }R} \right){\mathit{\boldsymbol{Q}}^{\rm{T}}}} \right)}_{u,k}}}}{{{{\left( {\left( {{\mathit{\boldsymbol{W}}_ \circ }\mathit{\boldsymbol{PQ}}} \right){\mathit{\boldsymbol{Q}}^{\rm{T}}}} \right)}_{u,k}}}} $

$ {q_{k,i}} \leftarrow {q_{k,i}}\frac{{{{\left( {{P^{\rm{T}}}\left( {{\mathit{\boldsymbol{W}}_ \circ }A} \right)} \right)}_{k,i}}}}{{{{\left( {{P^{\rm{T}}}\left( {{\mathit{\boldsymbol{W}}_ \circ }\mathit{\boldsymbol{PQ}}} \right)} \right)}_{k,i}}}} $

3.2 算法

算法1  NystrÖm方法的特征提取

输入:用户对电影的评分矩阵A。

输出:用户的特征矩阵P和电影的特征矩阵Q。

1) 根据少量的用户对电影的评分矩阵进行预测, 转化为${\mathit{\boldsymbol{\hat A}}}$;

2) 将矩阵${\mathit{\boldsymbol{\hat A}}}$转化为用户与用户或者观众与观众的相似度矩阵B;

3) 根据统影响力采样:

$ {q_j} = \frac{{\sum\limits_{i = 1}^m {A{{\left( {i,j} \right)}^2}} }}{{\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {A{{\left( {i,j} \right)}^2}} } }} $

式中j = 1, 2, …, n;

4) 利用自适应采样从B中选择其中的前c列, 构成矩阵C∈R^n×c;

5) 利用NystrÖm方法的公式$\mathit{\boldsymbol{\tilde B}} = \mathit{\boldsymbol{CW}}_k^ + {\mathit{\boldsymbol{C}}^{\rm{T}}}$得到近似矩阵${\mathit{\boldsymbol{\tilde B}}}$;

6) 利用算法2得到电影的特征Q;

7) 用类似的方法得到用户的特征P;

returnP, Q, ${\tilde B}$

算法2 基于NystrÖm方法的矩阵恢复

输入:用户与电影的相似度矩阵B, 近似矩阵${\mathit{\boldsymbol{\tilde B}}}$

输出:电影的特征矩阵Q。

1) 用K-means方法初始化矩阵C。

2) 对矩阵${\mathit{\boldsymbol{\tilde B}}}$根据式(1)进行恢复;

3) 根据公式${\rm{min}}{\left\| {\mathit{\boldsymbol{\tilde B}}-\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{Q}}^{\rm{T}}}} \right\|^2}$计算矩阵Q;

return Q。

算法3 归一化的NMF算法

输入:用户的特征矩阵P, 电影的特征矩阵Q;

输出:用户和电影的各个特征。

1) 初始化特征矩阵P和Q, 特征个数f, λ_P、λ_Q, user1、user2, movie1、movie2。训练次数a=0, 最大训练次数b;

2) while收敛且a < b时do

user1=0;

user2=0;

movie1=0;

movie2=0;

end

3) for   B_k中的每个条目r_{u, i},

$ \tilde r = \sum\limits_{k = 1}^f {{p_{u,k}}{q_{k,i}}} ; $

4) for k to f

user1_{u, k}=user1_{u, k}+q_{k, i}r_{u, i};

user2_{u, k}=user2_{u, k}+${q_{k, i}}{{\tilde r}_{u, i}}$;

movie1_{k, i}=movie1_{k, i} +p_{u, k} r_{k, i};

movie2_{k, i}=movie2_{k, i} +${p_{u, k}}{{\tilde r}_{k, i}}$;

end for

end for

5) for  u中的每个条目

6) for  k to f do

user2_{u, k}=user2_{u, k}+|I_u|λ_Pp_{u, k};

update p_{u, k}=p_{u, k}(user1_{u, k}/ user2_{u, k});

end for

end for

7) for i中的每个条目

8) for k to f d

movie2_{k, i}=movie2_{k, i} +|U_i|λ_Qp_{k, i};

update q_{k, i}=q_{k, i} (movie1_{k, i}/ (movie2_{k, i});

end for

end for

t=t+1

end while

3.3 算法举例

假设用户对电影的评分矩阵如表 1, 观众只对自己看过的电影进行评分, 对于未看过的电影则没有进行评分, 观众根据对电影的喜好进行评分, 评分的范围为1~5。

表 2、3是根据本文提出的算法得到的用户和电影的特征, 以及各特征的系数。

假设用户对电影的评分矩阵是1个10×20的矩阵, NystrÖm采样后得到的是1个6×6的矩阵, 用户的特征矩阵P是1个大小为6×3的矩阵, 电影的特征矩阵Q是1个3×6的矩阵。首先, 用随机数对用户和电影的特征矩阵进行非负初始化。然后用NMF算法, 正则化系数λ_P和λ_Q为正常数, 举个例子, 如可以设置为0.1, 辅助矩阵user1、user2被初始化为大小为6×3的全1矩阵, movie1和movie2则被初始化为大小为3×6的全1矩阵, 这样做的好处是可以与用户和电影的特征矩阵P和Q相一致。举个简单的例子, 如特征p_{2, 3}, 它与a_{2, 1}和a_{2, 4}相关, 假设在遍历期间, ${{\hat a}_{2, 1}}$和${{\hat a}_{2, 5}}$为0.052和0.05, 因此user1_{2, 3}和user2_{2, 3}就可以表示为

$ \begin{array}{*{20}{c}} {{\rm{user}}{{\rm{1}}_{2,3}} = {q_{3,2}}{a_{2,1}} + {q_{3,5}}{a_{2,4}} = }\\ {0.06 \times 3 + 0.04 \times 3 = 0.3} \end{array} $

$ \begin{array}{*{20}{c}} {{\rm{user}}{{\rm{2}}_{2,3}} = {q_{3,2}}{{\hat a}_{2,1}} + {q_{3,5}}{{\hat a}_{2,4}} = }\\ {0.06 \times 0.052 + 0.04 \times 0.05 = 0.005\;12} \end{array} $

用户2中有4条记录已知, 已知|I₂| = 4, 因此

$ \begin{array}{*{20}{c}} {{p_{2,3}} = {p_{2,3}} \times {\rm{user}}{{\rm{1}}_{2,3}}/\left( {{\rm{user}}{{\rm{2}}_{2,3}} + \left| {{I_2}} \right|{\lambda _p}{p_{2,3}}} \right) = }\\ {0.18 \times 0.3/\left( {0.005\;12 + 4 \times 0.1 \times 0.18} \right)} \end{array} $

3.4 算法的性能尺度

推荐系统的评估尺度可以从预测的准确度以及预测的覆盖等方面来进行, 文中主要是从预测值与真实值的近似程度, 它可以直接反应模型是否捕获了给定数据的基本特征, 因此, 选用均方根误差(root mean square error, RMSE)和归一化平均绝对误差(normalized mean absolute error, NMAE)来衡量。RMSE是评价推系统常用的1个指标, 定义为

$ {\rm{RMSE}} = \frac{1}{{mn}}\left\| {{\mathit{\boldsymbol{A}}^ * } - \mathit{\boldsymbol{A}}} \right\| $

式中:矩阵A是原始的观众对电影的评分, A^*则表示预测填充后的矩阵。

NMAE也是推荐系统中经常使用的1个评价尺度, 用于测量目标数据集和预测数据集之间的绝对误差, 定义如下:

$ {\rm{NMAE}} = \left( {\frac{{\sum\nolimits_{\left( {u,i} \right) \in V} {{{\left| {{r_{u,i}} - {{\hat r}_{u,i}}} \right|}_{{\rm{abs}}}}} }}{V}} \right) $

式中|·|_abs表示绝对值。使用该符号来区分1个集合的基数。

4 实验及结果 4.1 实验设置

本文涉及的电影数据集中包含900个用户对1 500部电影的评分, 观众可能只观看自己感兴趣的电影并对其进行评分。为了保证推荐系统的高效性, 首先将矩阵A观众对电影的评分矩阵转化为电影与电影的相似度矩阵B, 对矩阵B进行自适应NystrÖm采样, 得到矩阵C以及${\mathit{\boldsymbol{\tilde B}}}$, 由于原始矩阵的稀疏性, 因此矩阵${\mathit{\boldsymbol{\tilde B}}}$也是稀疏的, 对自适应NystrÖm采样后得到的${\mathit{\boldsymbol{\tilde B}}}$根据不完全矩阵的恢复方法进行恢复, 得到矩阵${\mathit{\boldsymbol{\tilde B}}}$利用算法2得到电影的特征矩阵Q, 用同样的方法也可以得到用户的特征矩阵P, 最后根据算法3对用户的特征矩阵P和电影的特征Q进行分析, 得到其基向量以及各自所占的比重进行计算, 对用户未来感兴趣的电影进行推荐。与以下算法做比较。

1) NMF方法:NMF算法是推荐算法中一种常用的方法, 可以将原始矩阵分解为2个矩阵, 分别代表的是基以及基的比重。本文中, 若直接将用户的特征P和电影的特Q进行分解, 则得到的用户和电影的特征维数较高, 对于用户对电影评分类似的稀疏矩阵来说, 并不需要用到所有的特征, 只需要有限个明显的特征, 便可以根据这些特征来预测以及推荐。若直接用NMF方法, 虽然NMF可以将1个较大的矩阵分解为2个较小的矩阵, 但是由于原始评分矩阵的规模较大, 分解后的2个矩阵的规模也不小, 因此, 对内存以及计算的速度来说也是一个不小的挑战。

2) PCA方法:PCA是一种常用的特征选择的方法, 同时也是数据降维中常用的一种方法, 该方法能够将数据中的主要的元素和结构找出来, 将原始复杂的原始数据进行降维, 将原始数据背后隐藏的结构进行简化, 这种方法虽然简单, 但是对于大规模的稀疏矩阵来说, 该方法并不适用, 由于数据的规模较大且相对稀疏, 导致其特征的稀疏性, 不能准确直接分析出其潜在特征。

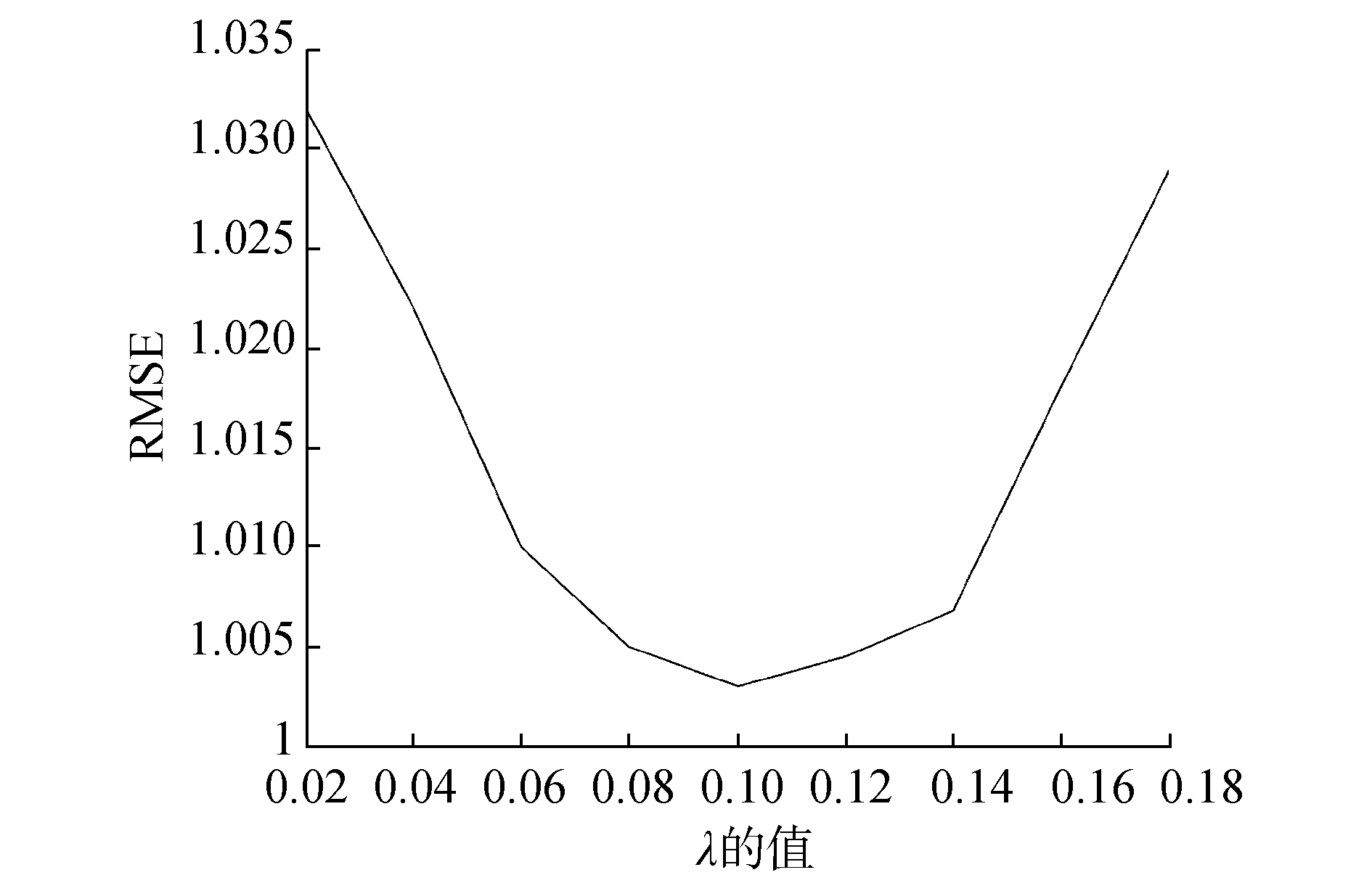
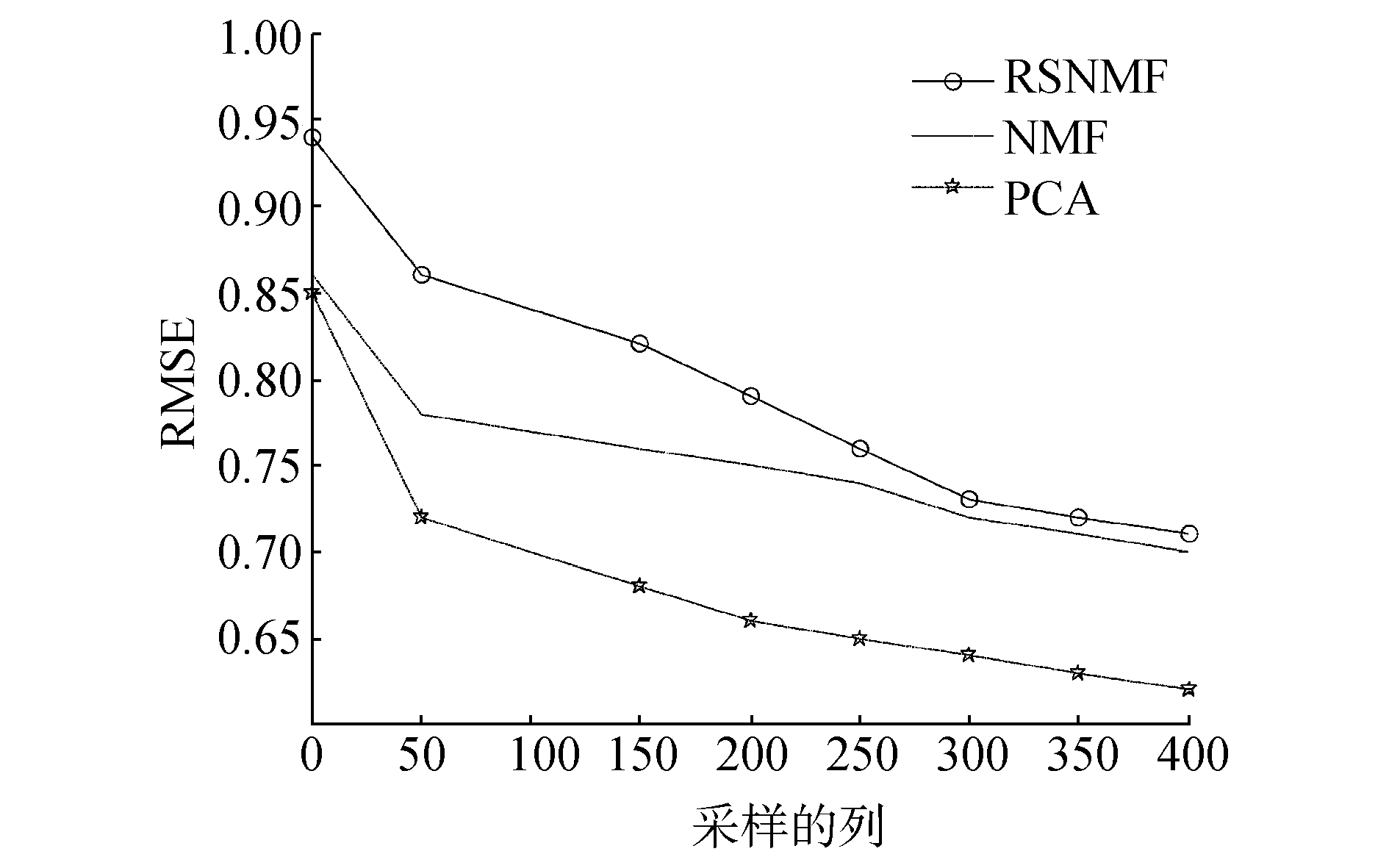
4.2 实验过程

实验中对数据集中的RMSE进行了测试。对数据集采样不同的列, RMSE也会不同。图 1所示是不同λ所对应的RMSE。图 2则表示的是采取相同列时各方法所对应的RMSE, 可以看出, 当采取相同的列时, 本文所提出算法的RMSE的效果更好。

4.3 实验结果分析

从表 4中可以看出, 对于不同的方法, 在不同的数据集上消耗的时间以及精度都有所不同, 相对于NMF和PCA, 本文提出的RNMF的性能更优越。本文用到的NystrÖm方法使得采样后的矩阵的规模减少了, NystrÖm方法的对象是对称的半正定矩阵, 因此, 只需要采取其中的列而已, 因此, 计算的时间减少了。精度的提高是因为本文中将原始的稀疏矩阵进行了填充, 这样分解得到的特征更具有代表性, 精度也会进一步提升。

5 结论

本文中通过基于NystrÖm方法的电影推荐算法与已有的算法进行了比较, 传统的NMF对非凸矩阵的效率较高, 本文中使用NystrÖm方法, 可以将原始的大规模矩阵降低到一个低维的子空间中, 计算量由原来的O(n³)降低到O(kcn), 由此可见, 对于大规模的矩阵来说, 使用NystrÖm方法的时间复杂度更小。

1) 本文主要针对的是对电影的推荐, 在未来的工作中, 会针对更多的商品进行推荐, 运用到更多的实际应用中, 这样可以大大节省用户遴选的时间, 也可以方便商家为用户进行推荐, 大大提高效率。

2) 由于电影矩阵的稀疏性, 要对用户对电影的评分矩阵进行填充以及采样, 虽然采样后的矩阵规模减少了, 但是填充的过程中也有很多工作要做, 导致计算的时间复杂度会有所增加, 因此, 在未来的工作中, 会在保证精度的同时又能够减少算法的时间复杂度, 减少运算的复杂度。