2. 哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001
2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
船舶水下噪声来源主要分为3部分:船舶机械振动产生的噪声、水动力噪声和螺旋桨振动诱发的噪声。其中水动力噪声是指船舶在航行过程中由于船体表面和水流边界面发生相对运动而引起的随机噪声和空化噪声等。现有研究舰船水动力噪声的手段较少,主要采用模型试验和数值模拟。
降低舰艇的水下辐射噪声不仅可以提高舰艇自身的隐蔽性,而且还可以增大自身声呐系统的作用距离,从而大大提高了舰艇的水下对抗能力。国内外许多学者对船体水下辐射噪声开展了大量的研究工作[1-12]。Seybert A.F等[1]建立了半空间边界积分方程,对声辐射和声散射问题进行了研究,并讨论了壁面对脉动球近场点声压的影响。徐张明等[2]采用边界元方法对船舶外壳面上的声强进行了预报分析,提供了一套预报振动噪声的方法。邹春平等[3]采用有限元/边界元方法对船舶水下辐射噪声特性进行了研究,所得的计算结果与试验值吻合较好。
雷诺平均方法现已能够较为准确地模拟船舶的三维黏性流场[6]。然而雷诺平均方法针对所有的尺度涡都用湍流模型来模拟,在一定程度上与客观事实不符,因此雷诺平均方法不能将流动过程中的微观湍流结构和涡结构展现出来。与雷诺平均方法不同,大涡模拟方法(LES)对不同尺度的涡采用不同的处理方式,对微小尺度涡引入湍流模型,而对大尺度涡则进行直接数值计算,因此大涡模拟方法在反映船舶真实流场方面具有一定优势。本研究采用大涡模拟方法对船舶流场进行数值模拟,之后加载FW-H声学模型运用类比方法模拟船舶的水下流噪声声场,研究船舶流动及声场特性,对进一步研究舰船噪声、优化船体型线和提升舰船隐身性都有着重要的指导意义。
1 数学模型湍流流场中的微观结构较为紊乱,决定流场特性的是大尺寸的漩涡,而小尺寸的漩涡主要造成湍流动量的扩散。大涡模拟(LES)是介于直接数值模拟方法和雷诺平均方法之间的一种数值模拟方法,LES对不同尺度的涡采用不同的处理方式,对微小尺度涡引入湍流模型,而对大尺度涡则进行直接数值计算。与直接数值模拟方法不同,LES方法引入湍流模型仅模拟小尺度的涡,因此计算数据较少,计算的效率较高。而与雷诺平均方法相比,保留了对大涡的直接数值计算,可以保留较多脉动行为信息,这样采用不同的手段处理不同尺度的涡,便能更加真实地反映流场信息,因此LES对研究船尾流噪声具有重要作用。
大涡模拟的控制方程由连续性方程及通过滤波函数处理而得的非定常N-S方程组成:
| $\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial (\rho {{\bar u}_i})}}{{\partial {x_i}}} = 0$ |
| $\frac{\partial }{{\partial t}}\left( {\rho {{\bar u}_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho {{\bar u}_i}{{\bar u}_j}} \right) = - \frac{{\partial \bar P}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left( {\mu \frac{{\partial {\sigma _{ij}}}}{{\partial {x_j}}}} \right) - \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}}$ |
| $\left\{ \begin{gathered} {\sigma _{ij}} = \left[ {\mu \left( {\frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}} + \frac{{\partial {{\bar u}_j}}}{{\partial {x_i}}}} \right)} \right] - \frac{2}{3}\mu \frac{{\partial {u_i}}}{{\partial {x_j}}}{\delta _{ij}} \\ {\tau _{ij}} = \rho \overline {{u_i}{u_j}} - \rho {{\bar u}_i}{{\bar u}_j} \quad\quad\quad\quad\quad\quad\\ \end{gathered} \right.$ |
式中:
Willimas与Hawkings在Curle方程的基础上进行扩展,加入广义函数并且考虑物面的作用,便得出FW-K方程:
| $\begin{aligned} \frac{1}{{{C_0}^2}}\frac{{{\partial ^2}p'}}{{\partial {t^2}}} - {\nabla ^2}p' =& \frac{{{\partial ^2}}}{{\partial {x_i}\partial {x_j}}}\left[ {{T_{ij}}H\left( f \right)} \right] - \\ &\frac{\partial }{{\partial {x_i}}}\left\{ {\left[ {{p_{ij}}{n_j} + \rho {u_i}({u_n} - {v_n})} \right]\delta (f)} \right\} +\quad\quad\\& \frac{\partial }{{\partial t}}\left\{ {\left[ {{\rho _0}{v_n} + \rho ({u_n} - {v_n})} \right]\delta (f)} \right\}\quad \quad\quad\quad\\ \end{aligned} $ |
式中:f代表空间区域,空间区域位置与其正负有关;ui、
计算模型为某内河双桨船,船模缩尺比
|
|
表 1 船型主尺度 |
基于Fluent软件构建数值水池对船舶三维黏性流场进行计算,在ANSYS的处理器中建立图1所示模型。建模过程中使用水平坐标系,X轴代表来流方向,船体采用单相流计算模型,即船体只取水线以下部分,流域入口取距离船首1倍船长,出口取2倍船长,水深设定为1倍船长,水池宽度为2倍船长。网格的质量直接影响到CFD计算精度,本文的计算网格采取全结构化网格,流域网格如图2所示。

|
Download:
|
| 图 1 船体建模 | |

|
Download:
|
| 图 2 流场网格划分 | |
在船体三维黏性流场的计算中,壁面采取标准壁面数处理,入口采用速度入口边界,出口边界定义为质量出口边界。在求解参数的设置上,先采用K-ω SST湍流模型进行定常水动力计算,等到获得稳定流场之后,再改用LES湍流模型进行非定常水动力计算。在计算时通常结合有限体积法来离散结构,扩散项则可以利用中心差分格式,压力速度耦合使用SIMPLEC算法,连续性曲线小于10−7时判定计算结果收敛,时间步长设定为5×10−4。
3 计算结果分析 3.1 流场计算结果及验证当大涡模拟计算收敛之后,将一定时间步长内的阻力求平均值,将不同航速下船体阻力的CFD计算值与试验值进行对比,如表2所示。
|
|
表 2 船模试验与数值模拟结果对比 |
通过表2中CFD计算值与试验值的对比可知,两者的吻合度很高,且计算值略微偏小,这是因为本研究采用的计算模型是单相流模型,未考虑船体兴波阻力的部分。表2的数据说明了采用的计算方法能够较为准确地模拟船体的黏性绕流场,LES模拟得到的流场初值是可信的。
对船体表面的速度场进行了分析,以航行速度U0=1.928 m/s为例,速度分布如图3所示。可以看出,船首部的流体流动速度很小,当流体流经船体后速度急剧增大,这一现象符合实际流动情况。

|
Download:
|
| 图 3 船体表面速度分布云图 | |
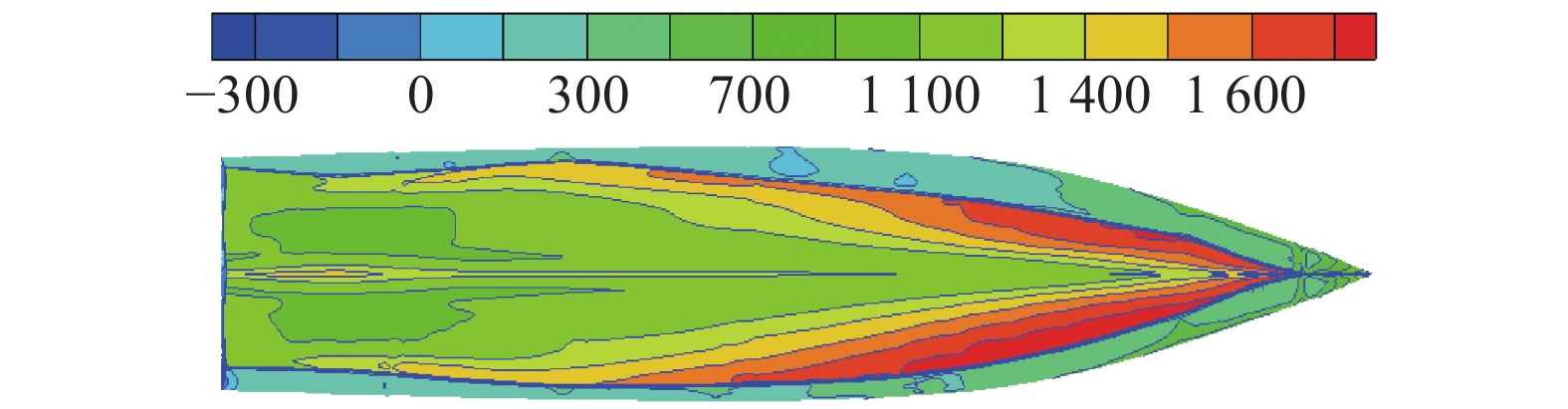
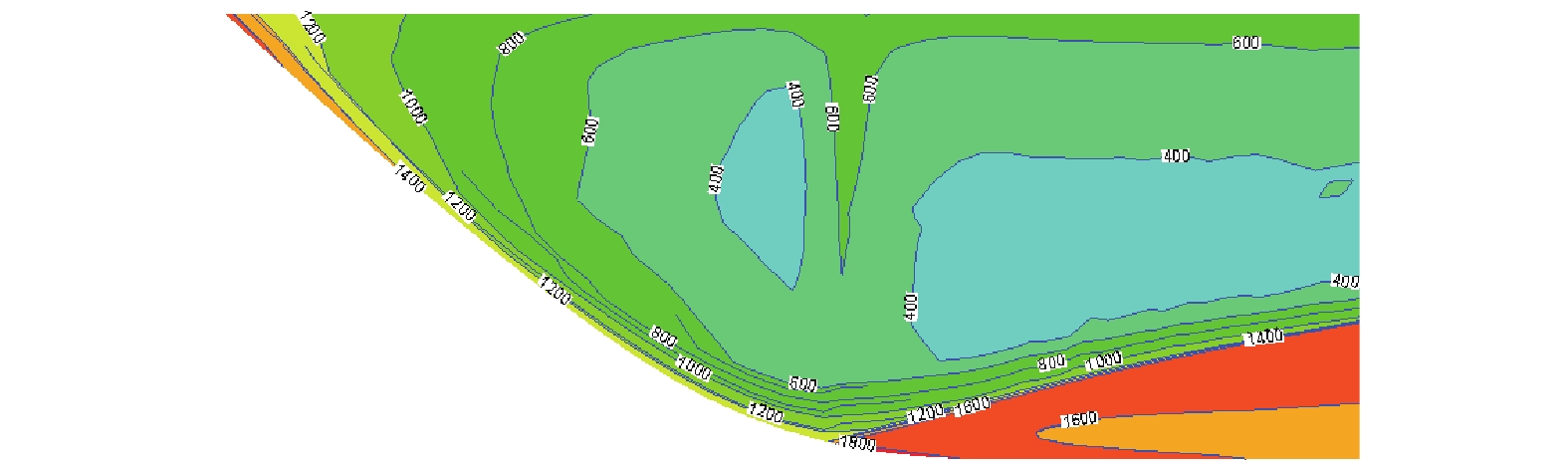
对船体表面压力场进行分析,同样以速度U0=1.928 m/s为例。由图4可知,船首底部两侧位置处压力明显高于其他区域,图5中显示船首最前缘也存在局部高压区,并且压力沿着船长方向逐渐减小。这是因为在这些部位流体的速度很低,当流场流过之后,速度迅速增大,压力也随着减小,符合伯努利方程的规律,速度分布等值图也很好地阐述了这一点。
|
Download:
|
| 图 4 船体表面压力云图 | |
|
Download:
|
| 图 5 船首部分压力云图 | |
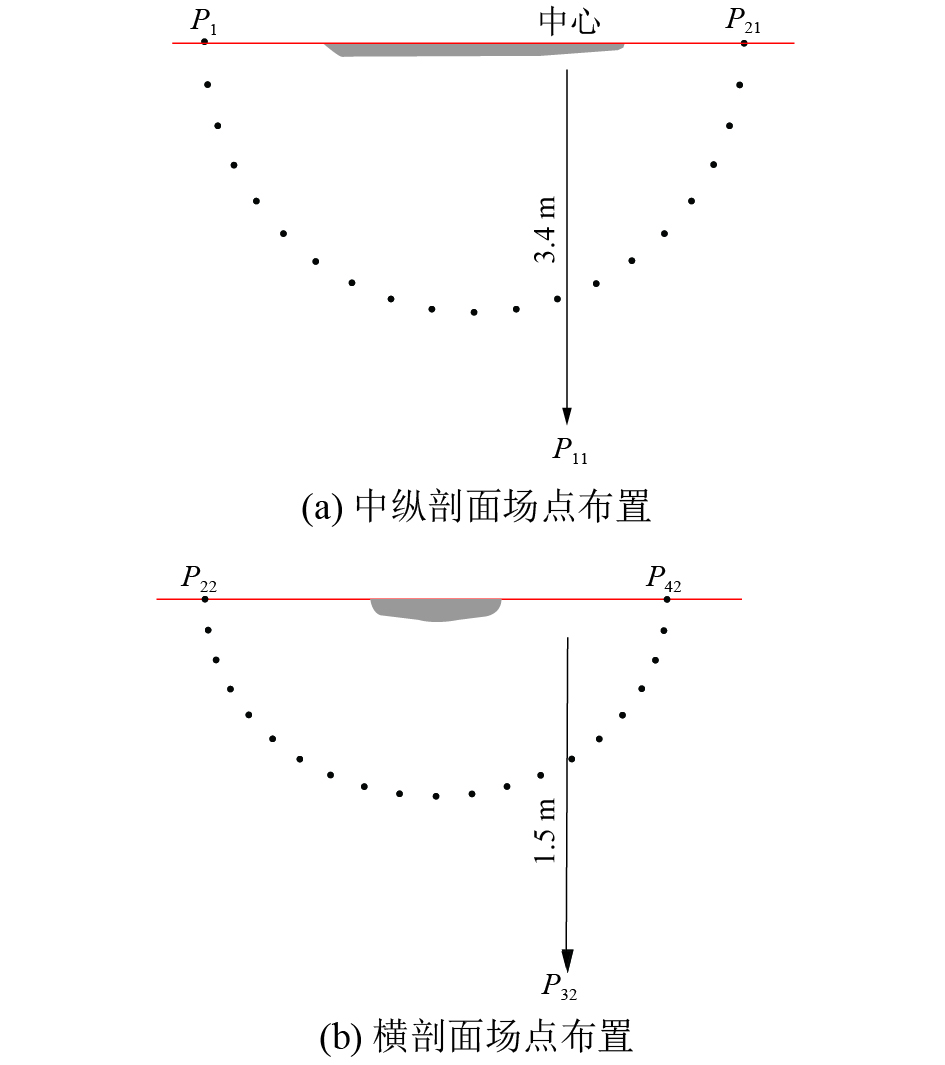
等到LES方法收敛后,考虑FW-H声学方程,对船体的噪声性能进行预报分析。以船体中心(0.013 8,0.166 7,0)为圆心,3.4 m为半径,在船体中纵剖面上均匀布置21个听水器,依次为P1~P21;以船尾后1.5 m处的(−3.386,0.166 7,0)为圆心,1.5 m为半径在船体的横剖面上均匀布置了21个听水器,依次为P22~P42;选取船体中心正下方2 m处,即(−1.986 2,0.166 7,0)为特征点P43,声场中的监测点分布如图6所示。
|
Download:
|
| 图 6 船体声场监测点分布 | |
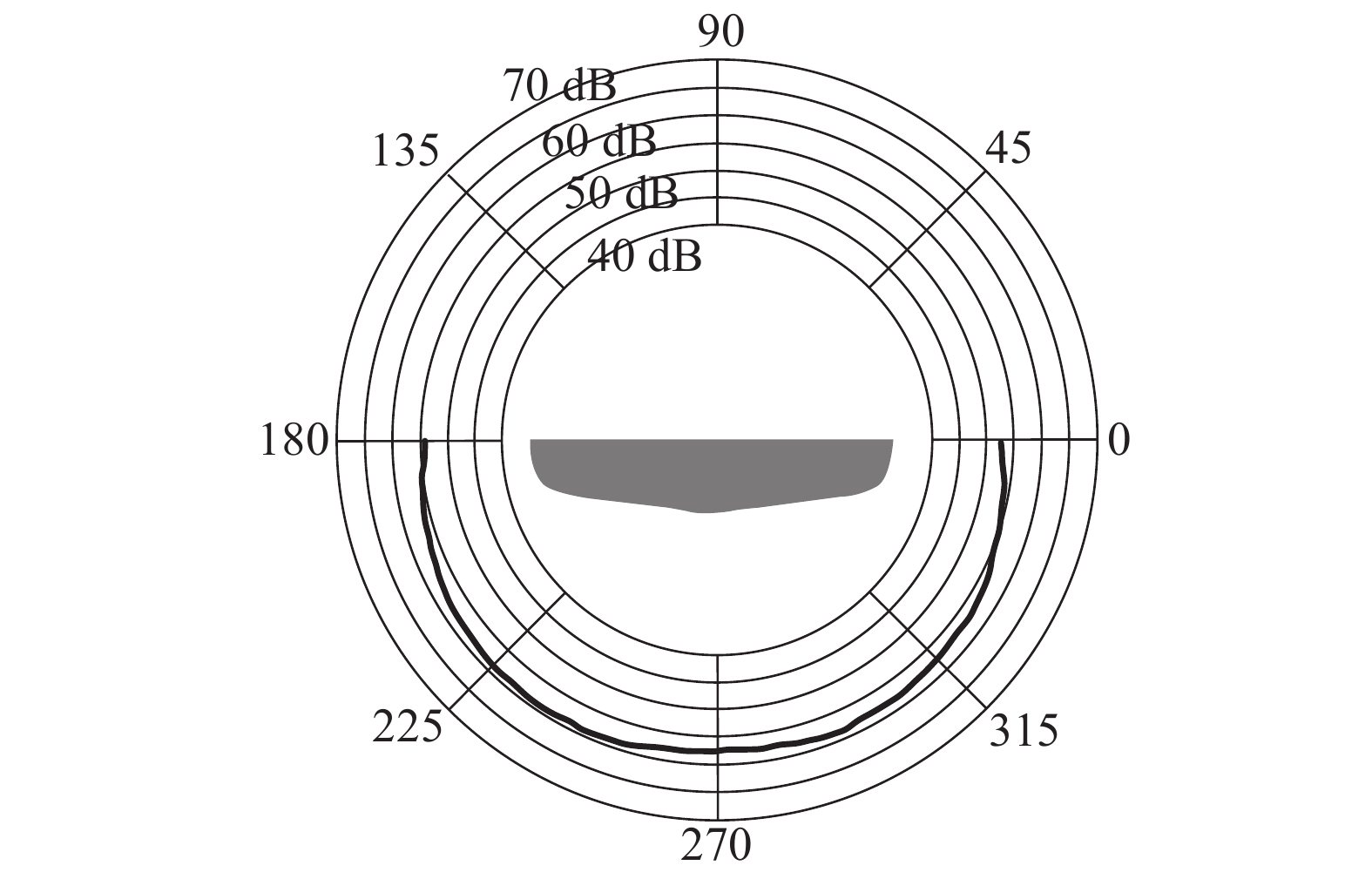
从声压级、噪声衰减特性以及声指向性等方面对船体水下辐射噪声进行了详尽地分析,获得了三维黏性流场中船体水动力噪声的基本特性。以航速U0=1.928 m/s为例,图7、8所示的分别是该航速下船体在中纵剖面上和横断面上各个监测点的总声压级。

|
Download:
|
| 图 7 船体水下噪声水平指向性图 | |
|
Download:
|
| 图 8 船体水下噪声垂直指向性图 | |
从图7、8可以看出,船体中纵剖面上的各监测点中,船尾的声压级最大,船首的声压级最小,分别为60.279 dB和44.3 dB,周向其他位置处的声压级大小几乎相等;船后1.5 m处的各监测点中,船体水平两侧的位置处声压级最小,为53.8 dB,其余各点的声压值相差不大,指向性不够明显。
由于波长的不同,在不同的振动频率下,噪声到达同一观测点的相位不同,叠加后噪声的指向性也是不同的。图9所示的是不同频率下船体水下辐射噪声垂直指向性。由图可知,在50 Hz时,其指向性还不是特别明显,仅船体正下方位置处的声压值较低。随着频率地增加,其指向性开始变强,并衍生出了3个波谷,分别位于船体水平两侧和正下方位置处,波峰位于水平和垂直方向的角平分线上,声指向性呈现出“ω”字形,船体的辐射噪声主要由四极子噪声组成,这与文献[3]和[4]揭示的规律基本吻合,结果满足定性一致。由于文献采用的船型及航速与本研究中使用的模型不相同,所以无法精确地进行定量比较。但从定性上来说,文中所提出的预报方法可以较为准确地预测三维黏性流场中船体的水动力噪声。

|
Download:
|
| 图 9 不同频率下船体水动力噪声垂直指向性图 | |
图10所示的是2个不同航速时噪声特征点的声压级曲线。由图可知,特征点的声压级随着航速的增大而增大,航速增大了0.794 m/s时,噪声级增大了约25 dB。黏性流场中船体的辐射噪声大多数发生在频率较低的阶段,而且噪声传播过程中的衰减规律是速度随着频率的增大而降低,当频率增大至600 Hz时,声衰减速度非常小,声级曲线基本保持平直,这与文献[4]的结论吻合度较高,符合声学规律,进一步验证了本文所采用的计算方法的可靠性。

|
Download:
|
| 图 10 不同航速时噪声特征点声压级曲线 | |
对某内河双桨船在三维粘性流场中进行了大涡模拟,并结合FW-H方程对船体的辐射声场进行了数值仿真,综合来看可以得出以下结论:
1)LES方法对不同尺度的涡采用不同的处理方式,能够将雷诺平均方法和直接数值模拟方法的优点结合起来,并且能够在一定程度上避免这两种方法的弊端,因此LES方法有着一定的可行性。
2)在本文的算例计算中,非定常计算结果与试验值能够很好地吻合,而且在声场仿真过程中,仿真的声压级曲线和声指向性图与有关文献相比较,也能够很好地吻合。
3)采用基于LES和FW-H方程耦合的方法能够较为准确地预报舰船的水动力噪声,可为准确预报舰船整体噪声提供参考。
| [1] |
SEYBERT A F, SOENARKO B. Radiation and scattering of acoustic waves from bodies of arbitrary shape in a three-dimensional half space[J]. Journal of vibration acoustics stress and reliability in design, 1988, 110(1): 112-117. DOI:10.1115/1.3269465 ( 0) 0)
|
| [2] |
徐张明, 汪玉, 华宏星, 等. 船舶结构的建模及水下振动和辐射噪声的FEM/BEM计算[J]. 船舶力学, 2002, 6(4): 89-95. DOI:10.3969/j.issn.1007-7294.2002.04.010 ( 0) 0)
|
| [3] |
邹春平, 陈端石, 华宏星. 船舶水下辐射噪声特性研究[J]. 船舶力学, 2004, 8(1): 112-124. ( 0) 0)
|
| [4] |
胡玉超. 舰艇结构声学设计与噪声预报技术研究[D]. 镇江: 江苏科技大学, 2012.
( 0) 0)
|
| [5] |
王炳和, 相敬林. 舰船水下声场边界元法建模与计算机模拟[J]. 计算机工程与应用, 2004, 40(7): 217-220. DOI:10.3321/j.issn:1002-8331.2004.07.066 ( 0) 0)
|
| [6] |
李良彦. 船舶阻力及黏性流场的数值模拟[D]. 大连: 大连理工大学, 2008.
( 0) 0)
|
| [7] |
陈伟杰, 乔渭阳, 王良锋, 等. 基于LES与FW-H方程的圆柱-翼型干涉噪声数值研究[J]. 航空动力学报, 2016, 31(9): 2146-2155. ( 0) 0)
|
| [8] |
高霄鹏, 杨国桢. 水面舰船流噪声基本声场的数值研究[J]. 海军工程大学学报, 2013, 25(1): 74-78. DOI:10.3969/j.issn.1674-5531.2013.01.018 ( 0) 0)
|
| [9] |
于汉, 李清, 杨德庆. 水面舰船黏性流场和流噪声的数值计算[J]. 中国舰船研究, 2017(6): 22-29. DOI:10.3969/j.issn.1673-3185.2017.06.004 ( 0) 0)
|
| [10] |
熊耀宇. 水面舰船绕流场与首部流噪声的数值计算研究[D]. 北京: 中国舰船研究院, 2011.
( 0) 0)
|
| [11] |
潘雨村, 张怀新. 用大涡模拟方法研究湍流边界层流动噪声[J]. 船舶力学, 2009, 13(6): 990-1001. DOI:10.3969/j.issn.1007-7294.2009.06.016 ( 0) 0)
|
| [12] |
樊林旭, 张磊, 陈德喜, 等. 水下潜器首部声基阵区流噪声研究方法[J]. 舰船科学技术, 2017, 39(7): 48-53. DOI:10.3404/j.issn.1672-7649.2017.07.010 ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


