2. 广东省大数据分析与处理重点实验室,广东 广州 510006;
3. 南昌工程学院 江西省协同感知与先进计算技术研究所,江西 南昌 330003
2. Guangdong Key Laboratory of Big Data Analysis and Processing, Guangzhou 510006, China;
3. Institute of Cooperative Sensing and Advanced Computing Technology, Nanchang Institute of Technology, Nanchang 330003, China
在过去数年中,由于在交通安全、交通效率以及车辆信息、娱乐等方面的一些突出应用,车载自组织网络已经成为部分研究人员[1-3]的重点研究方向。车载网是一种包含了车−车通信以及车−路通信的自组织网络[4]。带有路侧单元的车载网能够增加车载网中通信的可靠性,同时降低通信时延。但是,部署路侧单元的高成本已经成为车载网投入应用的巨大阻碍[5]。因此,部署需要在车载网的通信质量和其部署成本之间获得一个折中。文中提出了一种综合考虑连通性和部署成本的效用函数来获得优化部署方案。首先,引入了2种计算网络连通性的方法;之后提出了效用函数以获得部署方案。仿真结果表明,通过文中提出的效用函数,能够很好地在网络连通性和部署成本间去折中。
1 系统模型与问题分析 1.1 系统模型在文中,仿真模型考虑的是高速公路的场景,路侧单元被等间隔的部署在路边,如图1所示。令D为2个相邻路侧单元之间的距离,
| ${D_u} = D - 2 {R_u}$ |

|
Download:
|
| 图 1 系统模型 | |
令L为所部署的高速公路的长度。由于一般车辆通信半径远大于道路宽度,所以模型中忽略其宽度。
1.2 连通概率分析首先,假设2个相邻路侧单元之间的相邻车辆间距离服从指数分布。令
| $P\left( {x \leqslant {R_v}} \right) = 1 - {{\rm{e}}^{ - \lambda {R_v}}}$ |
由于相邻车辆间的距离是独立分布的,所以,可以得2车间距离大于
| ${P_c}{\rm{ = }}{\left( {{\rm{1 - }}{{\rm{e}}^{ - \lambda {R_v}}}} \right)^h}$ |
式中
通过上述分析,就能够知道上述的概率是在已知2车能够通信的条件下得到的,所以称其为必要条件下的连通概率,实际它是一个2车间能够通过车−车通信的上界。
其次,由于车−车的通信空间变化是呈一维空间分布的,它只有长度,没有宽度和高度,只能向两边无限延展。因此,能够计算2车间充分必要条件下的车辆能够通过车−车进行通信的概率为[8]
| ${P_c}\left( x \right) = \left\{ \begin{array}{l}1,0 \leqslant x \leqslant {R_v}\\\displaystyle\sum\limits_{i = 0}^{\left\lfloor {{x / {{R_v}}}} \right\rfloor } {\frac{{{{\left( { - \lambda {{\rm{e}}^{ - \lambda {R_v}}}\left( {x - i \times {R_v}} \right)} \right)}^i}}}{{i!}}} - \\{{\rm e}^{ - \lambda \times {R_v}}}\displaystyle\sum\limits_{i = 0}^{\left\lfloor {{x / {{R_v}}}} \right\rfloor - 1} {\frac{{{{\left( { - \lambda {{\rm{e}}^{ - \lambda {R_v}}}\left( {x - \left( {i + 1} \right){R_v}} \right)} \right)}^i}}}{{i!}},x \geqslant {R_v}} \end{array} \right.$ |
在部署的相邻的2个路侧单元间没有覆盖间隔,即
| ${N_{r\_\max }} = \left\lceil {\frac{L}{{2{R_u}}} + 1} \right\rceil $ |
因此,由
| $E = \frac{{{N_r}}}{{{N_{r\_\max }}}}$ |
由于相邻的2个路侧单元的覆盖间隔是大于等于0的,所以,可以得到E的范围为[0, 1]。最后,在折中考虑网络连通性和部署成本下,本文定义效用函数为[10]
| $U = \alpha E + \left( {1 - \alpha } \right){P_c}$ | (1) |
式中
为了评估在使用1.3节提出的效用函数进行路侧单元部署后对整个网络性能产生的影响,进行了一系列实验仿真。仿真场景中,道路总长为
对式(1)中的
本节首先验证了

|
Download:
|
| 图 2 不同α下的Du(L = 25 000 m, λ=1/100) | |
由
一般情况下,道路上车辆密度越大,则形成车−车通信的概率越大,从而网络的连通性越大。图3显示了在不同的车辆密度情况下
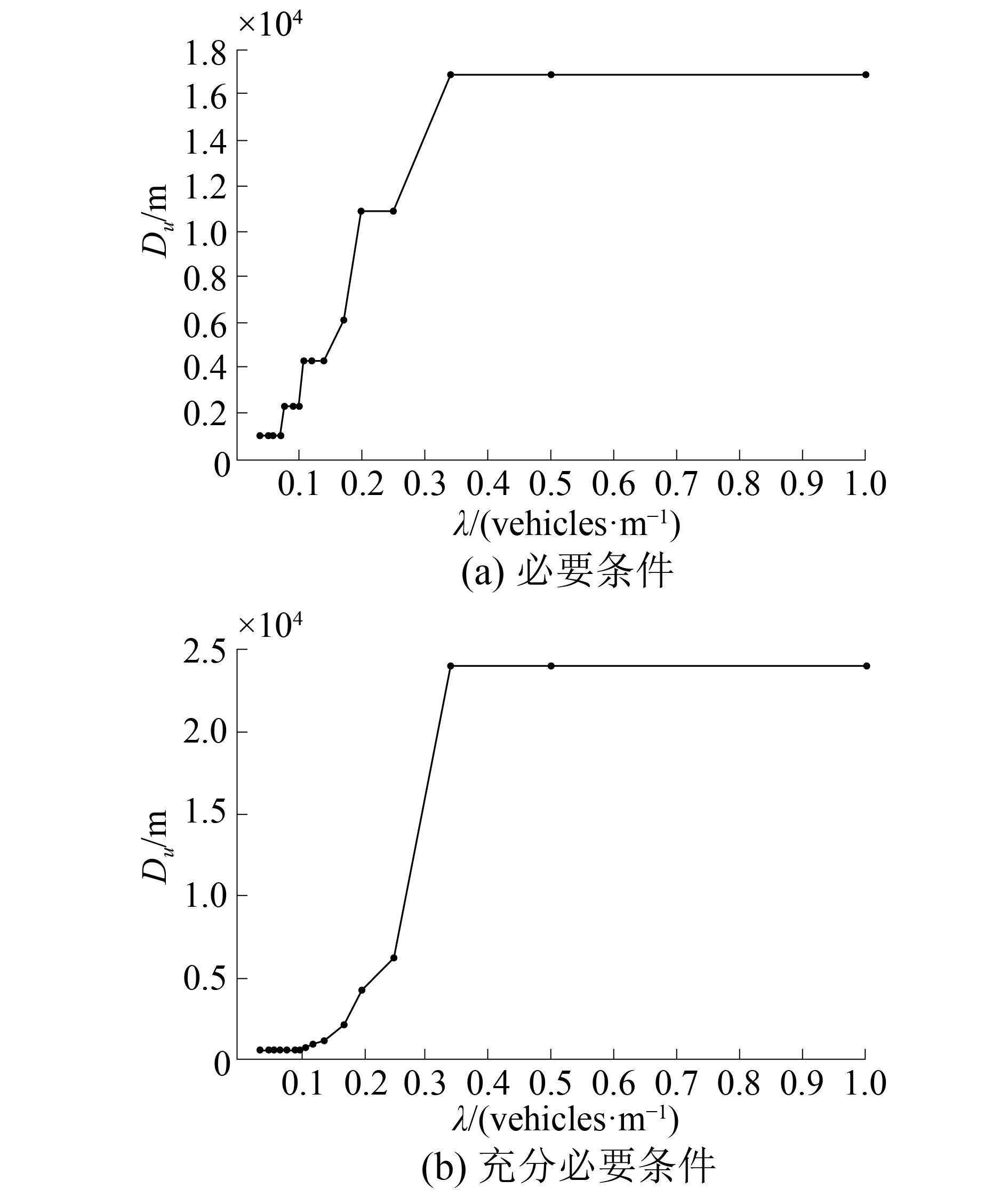
|
Download:
|
|
图 3 不同
|
|
根据前面的计算结果,可以得到在

|
Download:
|
|
图 4 不同
|
|
图5显示了发送包的平均端到端时延,可以看到时延在不同的
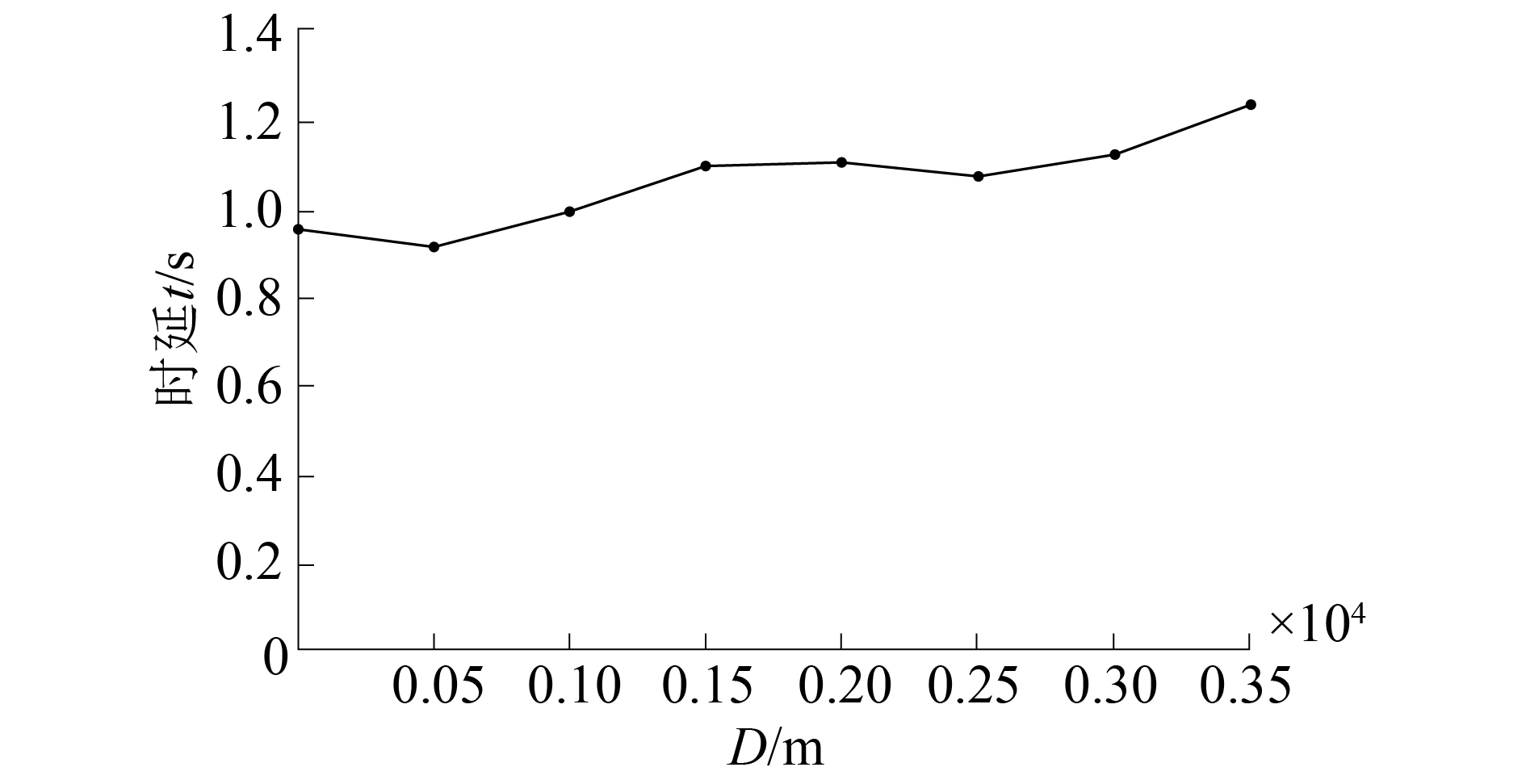
|
Download:
|
|
图 5 不同
|
|
文章旨在探究一种既保证车载网的通信质量,又可降低部署成本的车载网路侧单元部署方案。通过引入必要条件下的连通概率、充分必要条件下的连通概率2种网络连通性的方法,提出了效用函数以获得优化部署方案。仿真结果表明:1)提出的效用函数,能够在网络连通性和部署成本间实现折中优化;2)在同等通信质量下,该部署能够节约路侧单元的部署数量,对降低车载网的部署成本具有借鉴意义。由于高速公路环境下车载网的复杂性,文章目前的研究是在一维场景下的部署方案,对于二维场景的部署方案还有待后续研究。
| [1] |
HARTENSTEIN H, LABERTEAUX K P. A tutorial survey on vehicular ad hoc networks[J]. IEEE communications magazine, 2008, 46(6): 164-171. DOI:10.1109/MCOM.2008.4539481 ( 0) 0)
|
| [2] |
BARRACHINA J, GARRIDO P, FOGUE M, et al. Road side unit deployment: a density-based approach[J]. IEEE intelligent transportation systems magazine, 2013, 5(3): 30-39. DOI:10.1109/MITS.2013.2253159 ( 0) 0)
|
| [3] |
OTKOVIĆ I I, TOLLAZZI T, ŠRAML M. Calibration of microsimulation traffic model using neural network approach[J]. Expert systems with applications, 2013, 40(15): 5965-5974. DOI:10.1016/j.eswa.2013.05.003 ( 0) 0)
|
| [4] |
SIRAJ S, GUPTA A K, RINKU-BADGUJAR. Network simulation tools survey[J]. International journal of advanced research in computer and communication engineering, 2012, 1(4): 201-210. ( 0) 0)
|
| [5] |
BARBU V S, BULLA J, MARUOTTI A. Estimation of the stationary distribution of a Semi-Markov Chain[J]. Journal of reliability and statistical studies, 2012, 5: 15-26. ( 0) 0)
|
| [6] |
南春丽, 张伟, 刘喜元, 等. 一种卡尔曼滤波算法的无线传感器网络仿真模型[J]. 应用科技, 2015, 42(2): 48-52. ( 0) 0)
|
| [7] |
柴琳果, 蔡伯根, 王化深, 等. 车联网关键指标对车辆安全影响仿真测试方法[J]. 汽车工程, 2017, 39(11): 1316-1324. ( 0) 0)
|
| [8] |
曹蕾, 张欣, 杨大成. 频域均衡联合干扰删除的频域实现方法[J]. 电子科技大学学报, 2008, 37(6): 818-822. DOI:10.3969/j.issn.1001-0548.2008.06.005 ( 0) 0)
|
| [9] |
张永棠, 周富肯, 吴圣才. 精确农业无线传感器网络节点部署研究[J]. 江苏农业科学, 2017, 45(3): 200-205. ( 0) 0)
|
| [10] |
于冲, 赵海, 司帅宗, 等. 车载网运动模型的复杂网络解析方法[J]. 电子学报, 2017, 45(6): 1449-1455. DOI:10.3969/j.issn.0372-2112.2017.06.024 ( 0) 0)
|
| [11] |
ALSABAAN M, ALASMARY W, ALBASIR A, et al. Vehicular networks for a greener environment: a survey[J]. IEEE communications surveys and tutorials, 2013, 15(3): 1372-1388. DOI:10.1109/SURV.2012.101912.00184 ( 0) 0)
|
| [12] |
张永棠. 一种室内可见光通信系统MAC层协议的改进[J]. 应用科技, 2017, 44(1): 23-26. ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


