剩余使用寿命（remaining useful life，RUL）估计是设备预测与健康管理（prognostic and health management，PHM）的主要内容之一。准确估计设备RUL可以为维修决策提供基础数据，及时发现潜在威胁，从而采取相应措施有效避免故障的发生，对延长设备使用寿命、降低维护成本有重要意义^[1]。RUL估计方法可以分为基于模型、数据驱动方法2类。基于模型方法通过建立物理模型精确描述设备退化过程完成预测，由于需要掌握设备退化机理并对零部件精确建模，大多数情况下实现困难或代价极高^[2]；数据驱动方法从已失效设备的历史数据中，捕获传感器数据与设备退化水平之间的关系，完成RUL估计，在难以得到设备物理模型时依然可以实现RUL估计，通用性强。目前神经网络、支持向量回归、贝叶斯学习、隐马尔科夫模型^[3-8]等机器学习和统计学方法已经广泛应用于数据驱动的RUL估计。

1 基于退化曲线的RUL估计概述

基于相似性的方法属于数据驱动的RUL估计，其主要思想可以表述为：如果测试样本与参考样本有相似的退化性能，则它们可能有相似的RUL^[1]。测试样本指从尚未失效的设备（测试单元）中提取的样本，参考样本指从运行在相同工作条件下已经失效的设备（训练单元）中提取的历史样本。

图1描述了基于相似形状匹配的RUL估计总体框架。离线阶段，首先对训练单元传感器数据进行噪声滤波与信息融合，将其映射为一维健康度（health indicator，HI），拟合各训练单元随时间变化的HI轨迹以表示退化过程。然后从HI轨迹中提取曲线放入参考样本库中供在线RUL估计使用。在线阶段，对测试单元传感器数据进行相同的处理提取测试样本，将测试样本与参考样本库匹配，估计RUL。

参考样本的提取方法多样，文献[7]使用训练单元整个生命周期的HI轨迹作为参考样本匹配计算测试单元RUL；考虑到随着运行时间的增加，设备退化特征逐步明显，文献[8]使用末端HI轨迹作为参考样本进行剩余寿命估计。本文提取HI轨迹上固定时间长度的曲线作为参考样本，RUL估计不是基于测试单元HI轨迹的全部或末端，而是基于测试单元HI轨迹的某一部分，与传统相似性样本提取方法有显著差异。

2 曲线提取

本文所述剩余寿命估计方法需要处理训练单元和测试单元数据，为了减少计算量，在离散时间下进行数据处理，在整数时间点采样，间隔为1。假设有训练集合中含有N个训练单元，每个训练单元包含m类传感器数据，运行时间长度为 $l$ 。

2.1 HI轨迹转换

通用的健康度一般要求 ${\delta _{{\rm{HI}}}} \in [0,1]$ ，其中0代表设备失效，1代表设备完好^[9]。通过统计训练单元寿命分布，确定表示设备完好的剩余寿命阈值 ${R_{{\rm{th}}}}$ 后，训练单元实际健康度可表示为

${\delta _{{\rm{HI}}}}({t}) = (l - t)/{R_{{\rm{th}}}},1 \leqslant t \leqslant l$

(1)

对N个训练单元所有时间点传感器数据和实际健康度进行线性回归处理^[2]，计算回归参数。各时间点健康度可由式（1）估计得出：

${\hat \delta _{{\rm{HI}}}} = \alpha + {{\beta}} {{{x}}^{\rm{T}}} = \alpha + \sum {_1^m} {\beta _i}{x_i}$

(2)

式中 ${{x}} = [{x_1},{x_2}, \cdots ,{x_m}]$ 表示m维传感器数据， $ [\alpha ,{{\beta}} ] =$ $ [\alpha ,{\beta _1},{\beta _2}, \cdots ,{\beta _m}]$ 表示m+1维线性回归参数。然后，对每个训练单元HI轨迹进行三阶多项式拟合，最终其HI轨迹可表示为 ${{T}} = [t_1 ,t_2 , \cdots ,t_l ]$ ， $t_i $ 表示训练单元在第i点的健康度。

2.2 HI子轨迹提取

参考曲线 ${{S}}$ 由元胞数组 $[{{s}},\tau ,\mu ]$ 完全定义，即： ${{S}} = [{{s}},\tau ,\mu ]$ 。其中 ${{s}} = [{s_1},{s_2}, \cdots ,{s_{{l_s}}}]$ 表示一段固定长度为 ${l_s}$ 的HI子轨迹， $\tau $ 表示距离阈值， $\mu $ 表示当测试单元相同时间长度HI子轨迹与 ${{s}}$ 之间距离小于距离阈值时，该测试单元的RUL估计值，其值根据训练单元数据确定^[10]。

首先按照步进方式，从各训练单元中提取长度 ${l_s}$ 的HI子轨迹，则训练单元 ${{{T}}_i}$ 的所有子轨迹可表示为

${ {\mathcal {{T}}^i}}= {[{{t}}_1^i,{t}_2^i, \cdots ,{t}_{{l_i} - {l_s} + {\rm{1}}}^i]^{\rm{T}}} = \left[ {\begin{array}{*{20}{c}} {t_1^i}& \ldots &{t_{{l_s}}^i} \\ \vdots & \vdots & \vdots \\ {t_{{l_i} - {l_s} + 1}^i}& \cdots &{t_{{l_i}}^i} \end{array}} \right]$

式中：矩阵 ${{\mathcal{{ T}}}^i}$ 表示 ${{{T}}_i}$ 的子轨迹集合，行向量 ${{t}}_j^i$ 表示该训练单元第j条HI子轨迹。由于重叠提取，HI子轨迹总数会非常大，将所有HI子轨迹作为曲线，即无必要也不现实，应进一步提取具有代表性的HI子轨迹。

K-means聚类是一种基于划分的聚类方法，其目的是将n个点划分到K个聚类，使得每个点都属于离它最近的均值点对应的聚类，算法过程如下：

1）从数据集中随机选择K个点作为初始聚类中心；

2）计算剩余数据到各聚类中心之间的距离，并将其分配给最近的类；

3）计算上一步得到聚类中每一类的图心，作为新的聚类中心；

4）重复步骤2）~3）直到新的聚类中心等于原聚类中心。

上述算法存在的问题是其聚类效果很大程度上依赖于初始均值点的选取，容易陷入局部最优，往往需要进行多次聚类选取满意的结果^[11]。2007年由D.Arthur等^[12]提出K-Means++算法对上述过程的第1步进行了改进，算法过程如下：

1）从数据集中随机选择1个点作为聚类中心；

2）计算剩余数据到已有均值点之间的最小距离 $D(x)$ ；

3）增选剩余数据中 $D(x)$ 最大的点为聚类中心；

4）重复步骤2）~3）直到选择出共K个聚类中心。

K-Means++算法提高了聚类效果的稳定性，本文使用此算法将HI子轨迹聚为 $p$ 类，选择每一类的中心点作为参考曲线 ${{S}}$ 的HI轨迹参数 ${{s}}$ 。

2.3 曲线参数 $\tau ,\mu $ 确定

通过以上步骤获得了参考曲线的参数 $s$ ，定义参考曲线 ${{S}}$ 与训练单元子轨迹集合 ${\mathcal{T}}$ 之间的最佳匹配为 ${{b}} = {[d,\;\rho ]^{\rm{T}}}$ ，其中 $d$ 表示 ${{s}}$ 与 ${\mathcal{T}}$ 行向量之间的最小欧氏距离， $\rho $ 表示取得最小距离时的HI子轨迹首个时间点对应的实际剩余使用寿命，由式（3）计算得出：

$\left\{ \begin{gathered} d = \mathop {\min }\limits_{1 \leqslant i \leqslant l - {l_s} + 1} {\left\| {{{s}} - {{{t}}_i}} \right\|_2} \hfill \\ \rho = l - \arg \mathop {\min }\limits_{1 \leqslant i \leqslant l - {l_s} + 1} {\left\| {{{s}} - {{{t}}_i}} \right\|_2} \hfill \\ \end{gathered} \right.$

(3)

参考曲线 ${{S}}$ 与训练单元 $[{{{T}}_1},{{{T}}_2}, \cdots ,{{{T}}_N}]$ 的最佳匹配集合B可表示为

${{B}} = {[{{b}}_1 ,{{b}}_2 ,...,{{b}}_N ]^{\rm T}} = \left[ {\begin{array}{*{20}{c}} {d_1 } \\ \vdots \\ {d_N } \end{array}\begin{array}{*{20}{c}} {\rho _1 } \\ \vdots \\ {\rho _N } \end{array}} \right]$

(4)

对式（4）第2列元素进行零均值归一化，并按照第1列增序进行行排列后变为

${{B}} = \left[ {\begin{array}{*{20}{c}} {d_{1'} } \\ \vdots \\ {d_{N'} } \end{array}\begin{array}{*{20}{c}} {\rho _{1'} } \\ \vdots \\ {\rho _{N'} } \end{array}} \right]$

定义参数 $k$ 为

$k = \arg \mathop {\min }\limits_{2 \leqslant j \leqslant N} \operatorname{var} [\rho _{1'} ,...,\rho _{j'} ]$

则参考曲线 ${{S}}$ 的参数 ${\tau _{}} = d_k ,{\mu _{}} = 1/k\sum\limits_{j = 1}^k {\rho _j } $ 。至此，参考曲线 ${{S}}$ 的3个参数已完全确定，重复以上步骤可确定 $p$ 类曲线的参数。进一步，设定距离阈值限制参数 $\alpha $ ，通过抛弃参数 $\tau > \alpha $ 的参考曲线提高匹配精度，最终参考样本库中将包含q类曲线。

3 剩余寿命估计与预测性能评价

每个测试单元同样包含m类传感器信息，运行时间长度为 ${l_t}$ 。第0点代表设备首次运行时刻，第 ${l_t}$ 点代表监测数据停止时刻而不是设备失效时刻。RUL估计的目的是从有限时间的监测数据中估计出设备的失效时间。

3.1 剩余寿命估计

在对传感器数据做干扰均值滤波处理后，由式（2）计算各时间点健康度，并拟合HI轨迹，测试单元的HI轨迹可表示为 ${{W}} = [{w_1},\;{w_2},\; \cdots ,\;{w_{{l_t}}}]$ ，测试单元长度为 ${l_s}$ 的子轨迹集合可表示为 $\mathcal{W} = [{\mathcal{W}_1},\;{\small\mathcal{W}_2}, \;\cdots , \;$ $ {\mathcal{W}_{{l_t} - {l_s} + 1}}]$ 。 ${\mathcal{}w_1}$ 计算所有参考曲线与测试单元HI子轨迹间的欧氏距离集合：

${{E}} = \left[ {\begin{array}{*{20}{c}} {{e_{1,1}}}& \ldots &{{e_{1,{l_t} - {l_s} + 1}}} \\ \vdots & \vdots & \vdots \\ {{e_{q,1}}}& \cdots &{{e_{q,{l_t} - {l_s} + 1}}} \end{array}} \right]$

式中 ${e_{ij}}{\rm{ = }}{\left\| {{{{s}}_i} - {{\mathcal{}}w_j}} \right\|_2}$ 为参考曲线 ${{{S}}_i}$ 与测试单元第j条HI子轨迹 ${\mathcal{}w_j}$ 之间的欧氏距离。定义 ${e_i}$ 为第i行的最小值， ${c_i}$ 为取最小值时的列序号，则 $[{{{S}}_1},\;{{{S}}_2}, \;\cdots ,\;{{{S}}_q}]$ 与 ${{W}}$ 的最佳匹配距离及时间可表示为

${{E'}} = \left[ {\begin{array}{*{20}{c}} {{e_1}} \\ \vdots \\ {{e_q}} \end{array}\begin{array}{*{20}{c}} {{c_1}} \\ \vdots \\ {{c_q}} \end{array}} \right]$

若 ${e_i} < {\tau _i}$ ，说明参考曲线 ${{{S}}_i}$ 可用于估计测试单元RUL，存储 $[{c_i},{\mu _i}]$ 。假设最终存储了k类曲线的数据，以距离阈值为自变量为对参考曲线 ${{{S}}_i}$ 的预测结果进行加权处理，则测试单元预测失效时间 ${\hat t_e}$ 及预测剩余寿命 $\hat r$ 可以表示为

$\left\{ \begin{gathered} {{\hat t}_e} = \sum\limits_{i = 1}^k {\frac{{{\tau _i}}}{{\sum\limits_{j = 1}^k {{\tau _j}} }}({c_i} + } {\mu _i}) \hfill \\ \hat r = {t_e} - {l_t} \hfill \\ \end{gathered} \right.$

3.2 预测性能评价

定义预测性能评价标准：

$\begin{gathered} {\varepsilon _i} = {{\hat r}_i} - {r_i} \hfill \\ {\eta _i} = \left\{ \begin{gathered} \exp [({r_i} - {{\hat r}_i})/13] - 1,\;{\rm{ }}{{\hat r}_i} - {r_i} \leqslant 0 \hfill \\ \exp [({{\hat r}_i} - {r_i})/10] - 1,\;{\rm{ }}{{\hat r}_i} - {r_i} > 0 \hfill \\ \end{gathered} \right. \hfill \\ \bar \eta = \sum\limits_{i = 1}^n {{\eta _i}} /n \hfill \\ \end{gathered} $

式中： ${r_i}$ 表示某测试单元实际RUL； ${\varepsilon _i}$ 为实际RUL与预测RUL之间的误差，是预测效果最直观的表示； ${\eta _i}$ 是PHM2008竞赛给出的评价方法^[2]，由于在实际生产中，设备突然失效造成的损失比提前检修或更换的花费要大的多，该方法对RUL估计值大于真实RUL的滞后型预测给出了更大的惩罚分数； $\bar \eta $ 表示所有预测单元得分的平均值，数值越小，预测性能越优。

4 案例分析

为验证本文提出方法的有效性，使用NASA预测数据资源库中的航空涡扇发动机数据集的FD001子集进行RUL预测。FD001模拟了单工况条件下、高压压气机退化导致的发动机失效过程，分为训练集和测试集各100个单元。每个单元数据来自同类型的不同发动机，每台发动机以不同的初始磨损和制造差异开始运行，这种磨损和差异被认为是制造过程中的正常情况。运行期间，高压压气机不断产生小故障，在训练集中，故障持续累积直至发动机失效；在测试集中，发动机在失效前停止运行。运行期间，通过21个传感器对相关表征参数持续监测，表征参数包括：风扇进口温度、低压压气机出口温度、高压压气机出口温度、风扇出口压力等，传感器数据均含噪音^[13]。通过对数据集样本长度进行统计，发现其训练集长度分布区间为 $[120,\;380]$ ，其中 $85\% $ 的单元分布区间为 $[150,\;250]$ 。测试集长度分布区间为 $[31,\;303]$ 。

4.1 传感器数据选择

通过观察21组传感器数据可以发现，其变化规律分为2类：一类随时间变化测量值成上升或下降趋势，能有效反应设备退化趋势，如图2（a）所示；另一类始终常值或随时间发散，无法反应设备退化趋势，如图2（b）所示。根据文献[7]，通过观察法选择传感器组合2、3、4、7、11、12、15作为RUL估计的原始传感器数据。

4.2 模型训练

由训练单元长度分布区间定义 ${R_{{\rm{th}}}} = 250$ 。使用均值滤波对各训练单元传感器进行降噪处理后，由式（1）计算每个时间点实际健康度 ${\delta _{{\rm{HI}}}}$ 。之后对100个训练单元共20 631个时间点进行多元线性回归处理，得到回归参数[α, β] = [176.6, −0.099, ..., −1.629]。由式（2）计算各点健康度 ${\hat \delta _{{\rm{HI}}}}$ 并进行3阶多项式拟合，得到HI退化轨迹 $[{{{T}}_1},{{{T}}_2}, \cdots ,{{{T}}_{100}}]$ ，如图3所示。

为保证参考曲线 ${{S}}$ 能与最短测试集进行匹配，定义 ${l_s}{\rm{ = }}20$ ，按照2.2、2.3节方法，改变聚类中心数量 $p \in $ {200, 250, 300, 350, 400, 450}，参数 $\tau $ 阈值 $\alpha \in $ {0.005, 0.01, 0.014, 0.016, 0.018, 0.02}建立不同大小参考样本库。按照3.2节所述，重复10次估计100个测试单元RUL，并进行预测性能评价，选取 $\bar \eta $ 最优的1次记入表1中。

从表中可以发现：随着聚类数量 $p$ 的增加 $\bar \eta $ 呈现降低的趋势，这是由于聚类数量增加后，有更多的原始曲线可与测试单元匹配。随着阈值 $\alpha $ 的增大， $\bar \eta $ 呈现先下降后增加的趋势。当 $\alpha $ 过小时，大量曲线被抛弃； $\alpha $ 过大时，一些分辨率不强的曲线被引入，这2种情况都会导致预测性能下降。从表中可知 $[p,\;\alpha ] = [450,\;0.018]$ 时，取得最低得分为7.1，以下分析基于此参数。

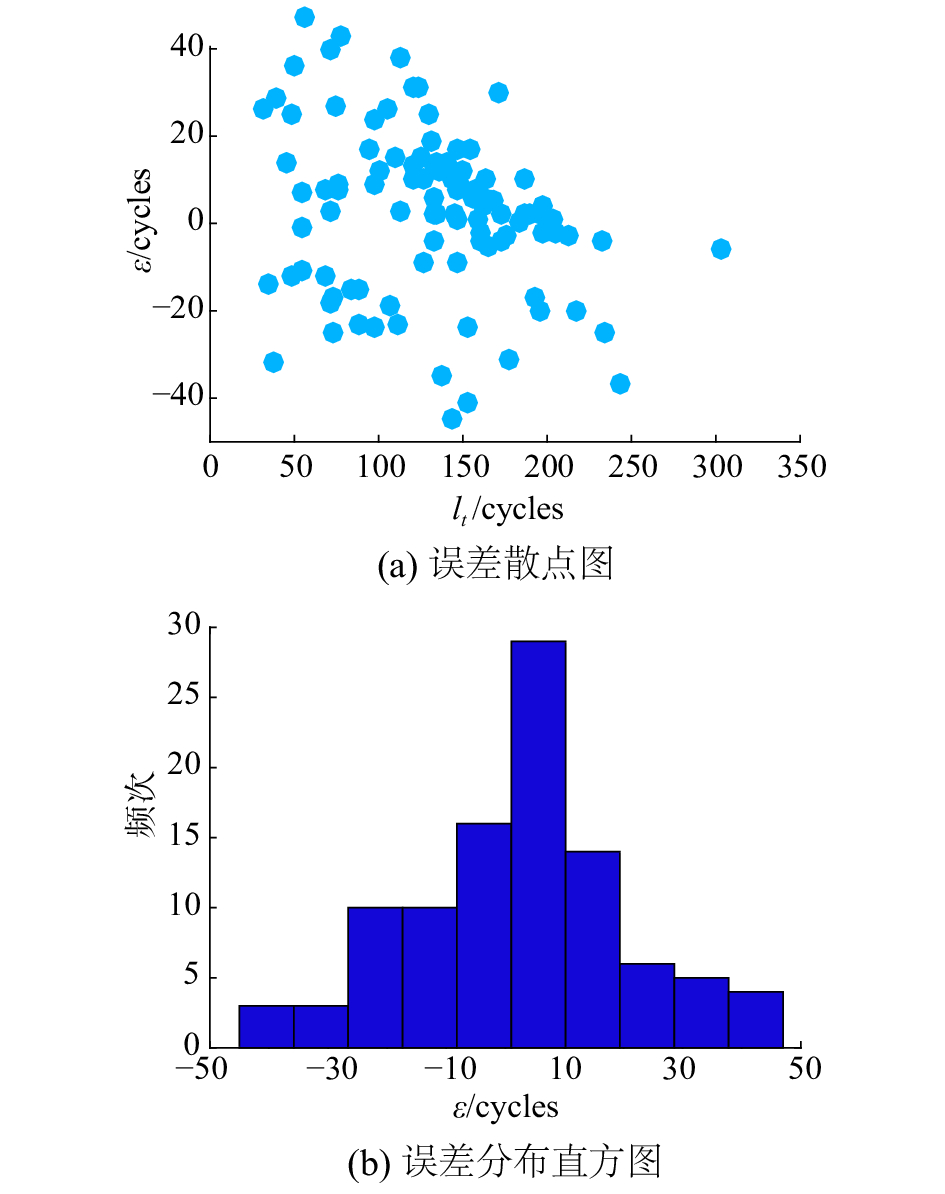
图4（a）给出了不同长度测试单元的误差散点图，可以看出 ${l_t} \in [31,\;150]$ 时预测误差发散， ${l_t} \in [150,\;240]$ 时预测误差逐渐变小，分析原因可能是由于绝大多数训练单元长度在[150, 250]，提高了该区域预测精度。由图4（b）可知误差分布范围在[-45, 47]。

为验证所提出的K-means++聚类方法有效性，在其他参数保持不变的情况下，使用常规K均值算法运行上述估计，重复10次估计测试单剩余寿命并计算评价得分 $\bar \eta $ 。表2给出了2种算法预测得分 $\bar \eta $ 的增序排列对比，可以看出常规K均值算法聚类稳定性差，影响了剩余寿命预测效果， $\bar \eta $ 分散在 $[7,\;25]$ 之间。采用K-means++算法的 $\bar \eta $ 集中在 $[7, 10]$ 之间，聚类稳定性有了极大的提升。预测效率方面上，采用常规K均值聚类的寿命估计程序平均运行时间为937 s，而K-means++方法平均运行时间1 424 s，劣势明显。在RUL估计领域对稳定性的要求显然高于效率，因此K-means++算法比传统K均值算法更适合应用到曲线聚类当中。

5 结论

本文针对设备剩余寿命预测问题，提出一种基于退化曲线相似性匹配的方法。

1）使用线性回归和多项式拟合方法将多维传感器参数融合为一维HI曲线，保留传感器退化信息的同时，简化了数据结构；

2）通过判别曲线与测试单元HI轨迹相关性，完成设备剩余寿命估计；

3）将K-means++聚类应用到上述方法中，极大提高了剩余寿命预测的稳定性。

实验结果表明，在大量历史数据可获取情况下，该方法预测精度较高、通用性强，可应用于机电系统关键部件（液压泵、作动筒、电作动器等）的剩余寿命估计。需要注意的是，退化曲线的提取直接影响最终RUL预测性能，如何改进多传感器数据融合方法、进一步提高曲线聚类稳定性，是今后研究的重点。