2. 92941部队93分队, 辽宁 葫芦岛 125000
2. 93 Team in 92941 Force, Huludao 125000, China
靶场试验中, 测试炮弹弹丸射程和射击精度均需要确定弹丸落点, 采用无线定位技术进行炮弹弹丸落点的自动检测大大提高了连发炮弹训练能力。但是炮弹落点前因无线信号受到外界环境因素定位精度不准确, 需要增加辅助落点外推预测手段。目前, 对炮弹落点数值积分法即对弹道方程做积分运算和系数解算法常用做炮弹外弹道外推预测落点, 因弹道方程是在一定假设条件下的简化处理模型。弹丸在空气中受到各种环境因素的影响, 弹道方程只是反映系统内部变化的规律, 与实际模型存在较大差距。因此, 为避开精确力学分析的繁琐[1], 本文采用炮弹定位的时间序列模型进行炮弹弹落点预报分析。
时间序列自回归分析与处理是近年来的一种新方法[2], 时间序列模型有3种:ARMA(autoregressive moving average)模型、AR(autoregressive)模型和MA(moving average)模型, 其中AR模型结构简单, 在某种意义上讲, 这3种可以相互转化, AR模型应用范围最广。但AR的常系数模型仅适用于平稳时间序列, 而时变自回归(TVAR)模型引入时变参数使得模型系数动态调整, 能够适应非平稳序列和平稳序列的各种变化, 省略了传统的非平稳时间序列建模中常用的数据预处理的平稳化过程, 并且提高模型的置信度[4], 已经在模态识别和故障诊断领域应用广泛。本文针对炮弹运动过程在X、Y、Z方向位置参数互不相关的情况, 分别建立这3个方向上自回归TVAR模型, 以炮弹高程Z向与靶面相交的时刻作为已知条件, 代入X、Y的TVAR模型, 从而求取炮弹的落点在靶面坐标下的位置。
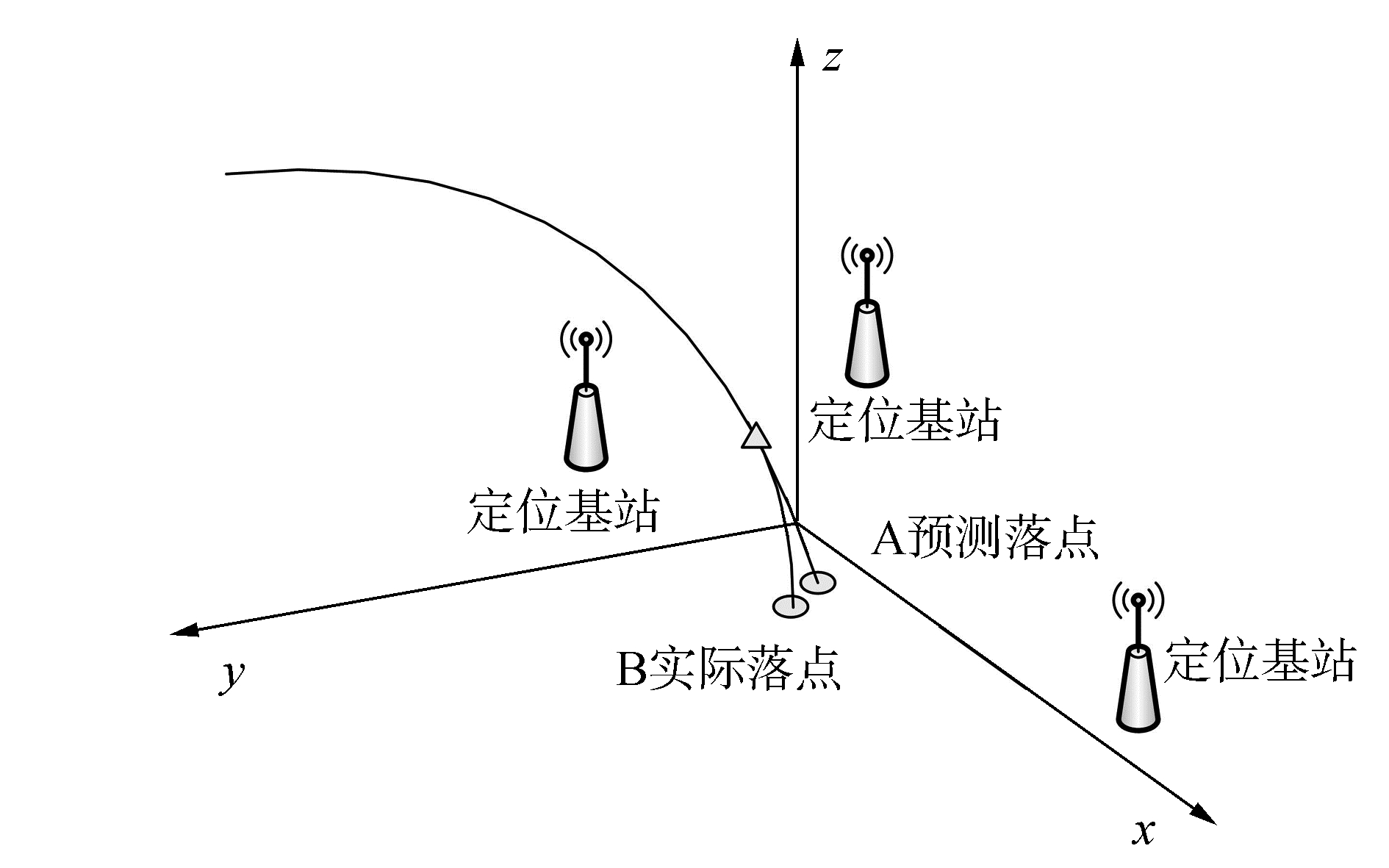
1 弹落点预报方法图 1所示为无线定位预测弹落点示意图, 利用弹载传感器和定位基站的协同到达时间差(time difference of arrival, TDOA)定位, 进行弹道位置参数运动过程的测量, 在图中“△”时, 因末段定位不准确或信号中断, 需要根据拟合历史点的时序模型预测目标的弹丸落点, 由于无线定位测量的炮弹位置在XYZ方向互不相关, 分别建立自回归TVAR模型, 以炮弹高程与靶平面XY相交的结束时刻为已知量, 代入求取X、Y在该时刻模型的落点位置, 从而得到落点在靶面的三维坐标。
|
Download:
|
| 图 1 无线基站协同定位预测弹落点示意 | |
AR模型是一种在描述时间序列方面特别有效的随机时间序列模型, 随机序列中下一个时间点的随机变量是由过去一个特定时间窗口内随机变量及白噪声平均值决定。对于短期预测来说, AR模型比ARMA模型具有参数少、计算简单、精度较高的特点。对于利用观测数据建立TVAR模型就需要对模型阶数和时变系数进行估计。
设零均值、p阶时变参数TVAR自回归模型如下:
| $ \begin{array}{l} {X_t} =- \sum\limits_{i = 1}^p {{\varphi _i}} \left( t \right){X_{t- i}} + {\varepsilon _t}\\ \;\;\;\;\;\;\;\;\;E\left[{{\varepsilon _t}} \right] = 0\\ E\left[{{\varepsilon _t}{\varepsilon _{t-i}}} \right] = \left\{ \begin{array}{l} 1, \;i = 0\\ 0, \;i \ne 0 \end{array} \right. \end{array} $ |
式中:t=1, 2, …, N, Xt是随机序列变量; φi(t)为AR模型时变估计系数; p是模型阶数; Xt仅与Xt-1, Xt-2, …Xt-p有线性关系; εt为服从N(0, σt2)的残差序列, 记为TVAR(p)。
2.1 模型阶数的估计TVAR模型阶次过高导致计算量增加, 实时性不好; 过低则建模精度不能反映信号内部的变化规律。因此, 需要选取模型的适当阶数。确定模型阶数的方法有残差方差图定阶法、F-检验定阶法、AIC准则、BIC准则等, 常使用的是基于最小信息准则的最佳函数法即AIC准则、BIC准则等。
| $ {\rm{AIC}准则的一般形式为} \\ \rm{AIC} = - 2 \times ln\left( {模型极大似然度} \right) + 2 \times \left( {参数个数} \right) $ |
对数似然函数与残差方差σε2的对数有着密切的联系。对于N个时序观测值中, 相应于TVAR模型的残差估计为
| $ \begin{array}{l} {\sigma _\varepsilon }^2\left( p \right) = \frac{{Q({{\hat \varphi }_1} \cdots {{\hat \varphi }_p})}}{{(N-p)-(p + 1)}}\\ \;\;\;\;\;\;\;\;\;\;Q = \sum\limits_{i = 1}^N {\tilde \varepsilon _i^2} \\ {{\tilde \varepsilon }_t} = {X_t}-{{\hat \varphi }_1}\left( t \right){X_{t - 1}} - \cdots {{\hat \varphi }_p}\left( t \right){X_{t - p}} \end{array} $ |
因此, AR(p)模型的AIC准则为
| $ {\rm{AIC}} = N{\rm{ln}}\left( {\mathop {\sigma _\varepsilon ^2}\limits^ \gg } \right) + 2\left( {p + 1} \right) $ |
为了弥补AIC准则的不足之处, Akaike于1976年提出了BIC准则, 如下
| $ {\rm{BIC}} = N{\rm{ln}}\left( {\mathop {\sigma _\varepsilon ^2}\limits^ \gg } \right) + \left( {p + 1} \right){\rm{ln}}N $ |
结合TVAR模型的系数变量估计和Akaike信息检验准则的AIC、BIC准则进行阶数最优选择。一般来说, lnN>2, 因此, 用AIC准则往往比用BIC准则确定的阶数高。本文选用AIC准则进行阶数确定。
2.2 模型时变系数的估计当TVAR时变模型阶数确定之后, 下一步关键就是确定准确的φi(t)和εt的方差。时变TVAR模型时变系数φi(t)假设由一些已知函数的线性加权组合近似。基函数选择正交函数, 可参看第4节的基时间函数选取, 线性表达式如下:
| $ {\varphi _i}\left( t \right) = \sum\limits_{j = 1}^m {{c_{ij}}{u_j}} \left( t \right) $ | (3) |
将其代入式(1), 整理为式(4)。
| $ {X_t} = {x_t}C + {\varepsilon _t} $ | (4) |
式中:
| $ \begin{array}{l} {x_t} = \left[{{u_1}\left( t \right){X_{t-1}} \ldots {u_m}\left( t \right){X_{t-1}}, \ldots, {u_1}\left( t \right){X_{t-p}}, \ldots, \;{u_m}\left( t \right){X_{t - p}}} \right]\\ \;\;\;\;\;\;\;\;\;\;\;C = {[{c_{11}}, \ldots, {c_{1m}}, \ldots, {c_{p1}}, \ldots {c_{pm}}]^{\rm{T}}} \end{array} $ |
如果采用传统最小二乘法对式(4)的时变参数估计, 则C的最小二乘估计为
| $ {{\mathit{\boldsymbol{\hat C}}} }={\left( {{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{x}}} \right)^{-1}}{\mathit{\boldsymbol{x}}^{\rm{T}}}X $ | (5) |
若要式(5)成立的充要条件是逆矩阵为非奇异矩阵, 因为模型中模型阶次p和时变参数m都是未知的; 工程实际中较多的可能性也会遇到x列间存在近似相关性, 这时LS的估计是不可信的。如果结合模型阶数的AIC确定准则, 对于时变TVAR模型拟定的p和m有较大结构维数, 因此从p×m个回归变量中选出主要变量, 只要使这些变量组成的模型达到正交矩阵, 那么模型的最终结构大最小二乘(LS)才是可信的。虽然可以使用Gram-Schmidt法进行式(4)正交分解, 从x中找出一组最小无关列, 就可以采用式(5)进行LS得出时变参数估计值, 但这种计算量会随着时间推移因结构庞大而增大, 且占用存储空间大。
因此本文利用递推最小二乘算法来求式(4), 令
| $ {\mathit{\boldsymbol{P}}_t} = {({\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{x}})^{-1}} $ | (6) |
则有如下递推算法,
| $ \begin{array}{l} {\mathit{\boldsymbol{P}}_{t + 1}} = {\mathit{\boldsymbol{P}}_t}-{\mathit{\boldsymbol{P}}_t}{\mathit{\boldsymbol{x}}_t}{(1 + {\mathit{\boldsymbol{x}}_t}^{\rm{T}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{x}}_t})^{-1}}{\mathit{\boldsymbol{x}}_t}^{\rm{T}}{\mathit{\boldsymbol{P}}_t}\\ {{\mathit{\boldsymbol{\hat C}}}_{t + 1}} = {{\mathit{\boldsymbol{\hat C}}}_\mathit{t}}-{\mathit{\boldsymbol{P}}_t}{\mathit{\boldsymbol{x}}_t}{(1 + {\mathit{\boldsymbol{x}}_t}^{\rm{T}}{\mathit{\boldsymbol{P}}_t}{\mathit{\boldsymbol{x}}_t})^{ - 1}}({\mathit{\boldsymbol{X}}_{t + 1}} + {\mathit{\boldsymbol{x}}_t}^{\rm{T}}{{\mathit{\boldsymbol{\hat C}}}_t}) \end{array} $ |
由于εt=Xt-φ1Xt-1-φ2Xt-2-…-φpXt-p, 则
| $ {\sigma ^2} = \frac{1}{{N-p}}\sum\limits_{t = p + 1}^N {} {\left( {{X_t}-\sum\limits_{i = 1}^p {{\varphi _i}} \left( t \right){X_{t-i}}} \right)^2} $ |
估计出φ(t), 按照式(2)就可以估计出σ2。
3 TVAR预测考虑用时间序列长期预测L步后的状态估计, 即根据已知n个时刻的序列观测值gj(t)=(t/T)j, gj(t)=(t/T)j, gj(t)=(t/T)j, gj(t)=(t/T)j, 对未来gj(t)=(t/T)j个时刻的序列值做出估计, 称为长期预测问题。首先利用模型估计时变系数, 按照该序列的历史数据构造方法, 获得点预测值。第gj(t)=(t/T)j时刻的预测值如式(7):
| $ {g_j}\left( t \right) = {\left( {t/T} \right)^j} $ | (7) |
式中gj(t)=(t/T)j时, gj(t)=(t/T)j。
4 基时间函数选取基时间函数是TVAR构造的重要问题, 目前, 常用的一些基函数有多项式基, 勒让德多项式、傅里叶基函数、离散余弦基函数等。TVAR模型建模是现代谱估计的重要工具[5], 映射至时域往往出现峰漂移现象, 因此选取基函数应依赖时间序列信号的特征, 如果信号是线性信号或者线性变化, 则上述基函数都适合; 如果信号周期性变化, 则余弦和傅里叶基函数是最佳选择; 如果特征不明显, 一般采用傅里叶基函数和多项式基函数进行TVAR参数估计[5]。公式如下:
1) 多项式基函数
| $ {g_j}\left( t \right) = {\left( {t/T} \right)^j} $ |
2) 傅里叶基函数
| $ {g_j}\left( t \right) = \left\{ \begin{array}{l} {\rm{cos}}\left( {\frac{{j{\rm{ \mathsf{ π} }}t}}{{2N}}} \right), \;\;\;\;j{为偶数}\\ {\rm{sin}}\frac{{\left( {j + 1} \right){\rm{ \mathsf{ π} }}t}}{{2N}}, \;j{为奇数} \end{array} \right. $ |
式中1 < t < T, T为观测时间内采样总数。
5 实验仿真为了验证上述TVAR算法的有效性, 使用一次外场炮弹实测数据进行算法验证。选取一组外测弹道实验数据, 即通过卫星系统信标差分计算出地理坐标下的高程时间序列测量值。如图 2所示, 取舰炮末端153个弹载定位的弹道测量点的高程信息, 来建立TVAR模型, 从图 2中可以看出, 其观测序列在280 m就没有数据。

|
Download:
|
| 图 2 高程观测序列 | |
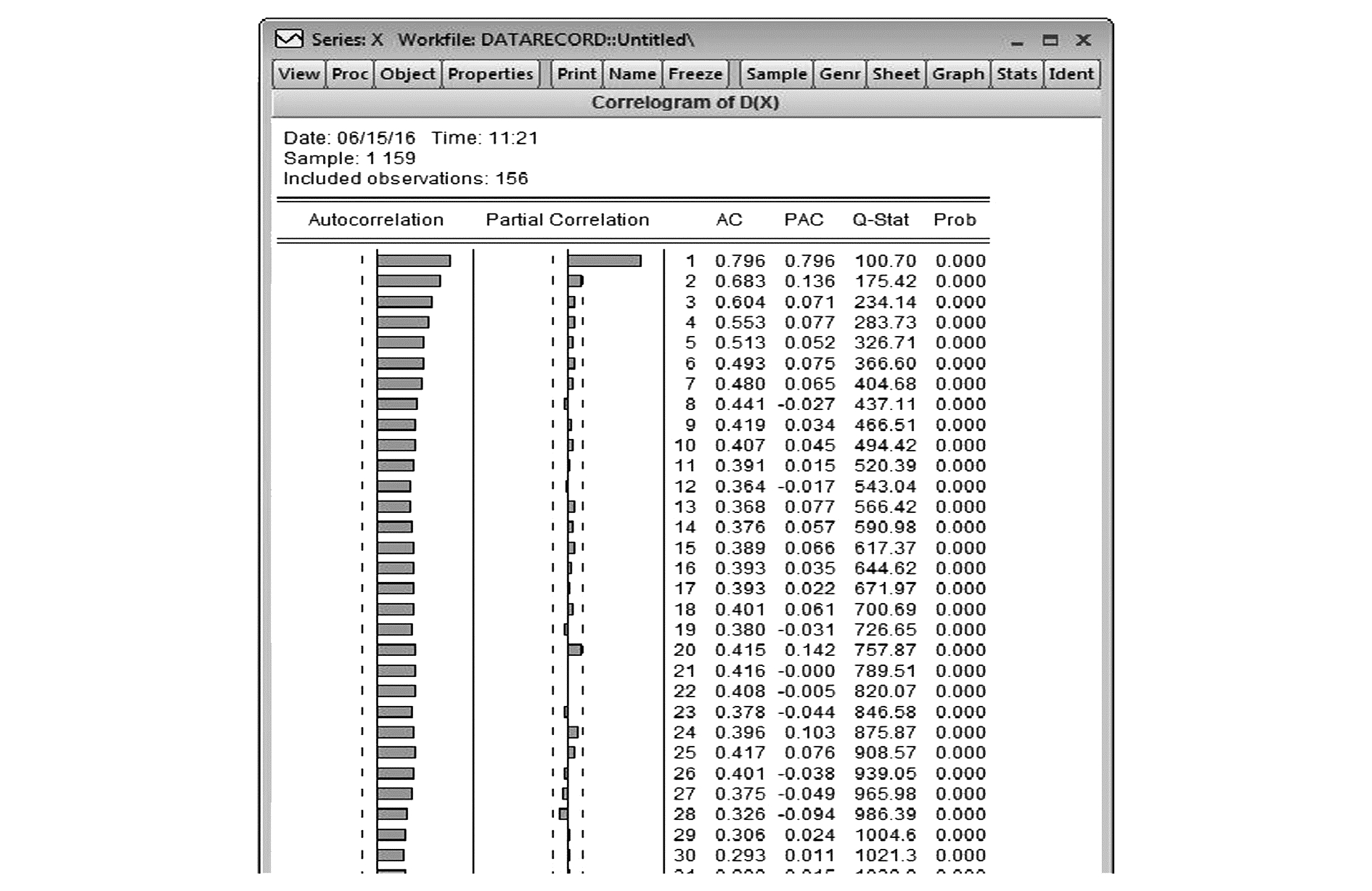
本文利用MATLAB和EVIEWS软件进行分析, 实验环境:Inter CPU2.93 G, 内存2 GB。经EVIEWS软件分析时间序列的样本自相关系数如图 3, 高程样本偏相关系数很快地落入barlett线内, 样本自相关函数基本呈现递减趋势, 但是没有落入barlett线内, 说明该序列是非平稳的。
|
Download:
|
| 图 3 高程序列样本的自相关系数和样本偏相关系数 | |
图 4为建立TVAR(p)高程数据模型的AIC曲线。首先进行模型结构辨识, 阶数p依次选取1~30, 使用傅里叶基函数分析, 选择AIC信息量准则最小的阶次作为模型的真实阶次。如图 4折中取法选择P=3, 模型AIC信息量偏小。

|
Download:
|
| 图 4 观测序列的AIC曲线 | |
对原始观测序列进行不同时间基函数的参数估计, 采用递推最小二乘算法估计变参数, 在相同时间参数和阶数条件下, 比较了不同基时间函数的选取对预测估计的影响。选定153个数据的前140个数据作为历史数据, 预测13步的高程信息, 最后进行模型预测估计值与观测值的偏差比较。图 5所示在设置阶数和基时间展开维数相同的条件下, 显示了不同时间基函数下的预测估计误差, 从图中可以看出, 采用傅里叶时间基函数对长预测时序比多项式时间基函数效果要好, 在时序5 s处多项式开始估计偏离, 产生误差累计; 同时, 采用了傅里叶时间基函数对TVAR的预测比常系数AR模型预测要准确, 究其原因在于TVAR非稳态时序的辨识过程是动态变化的。

|
Download:
|
| 图 5 不同时间基函数下的估计误差 | |
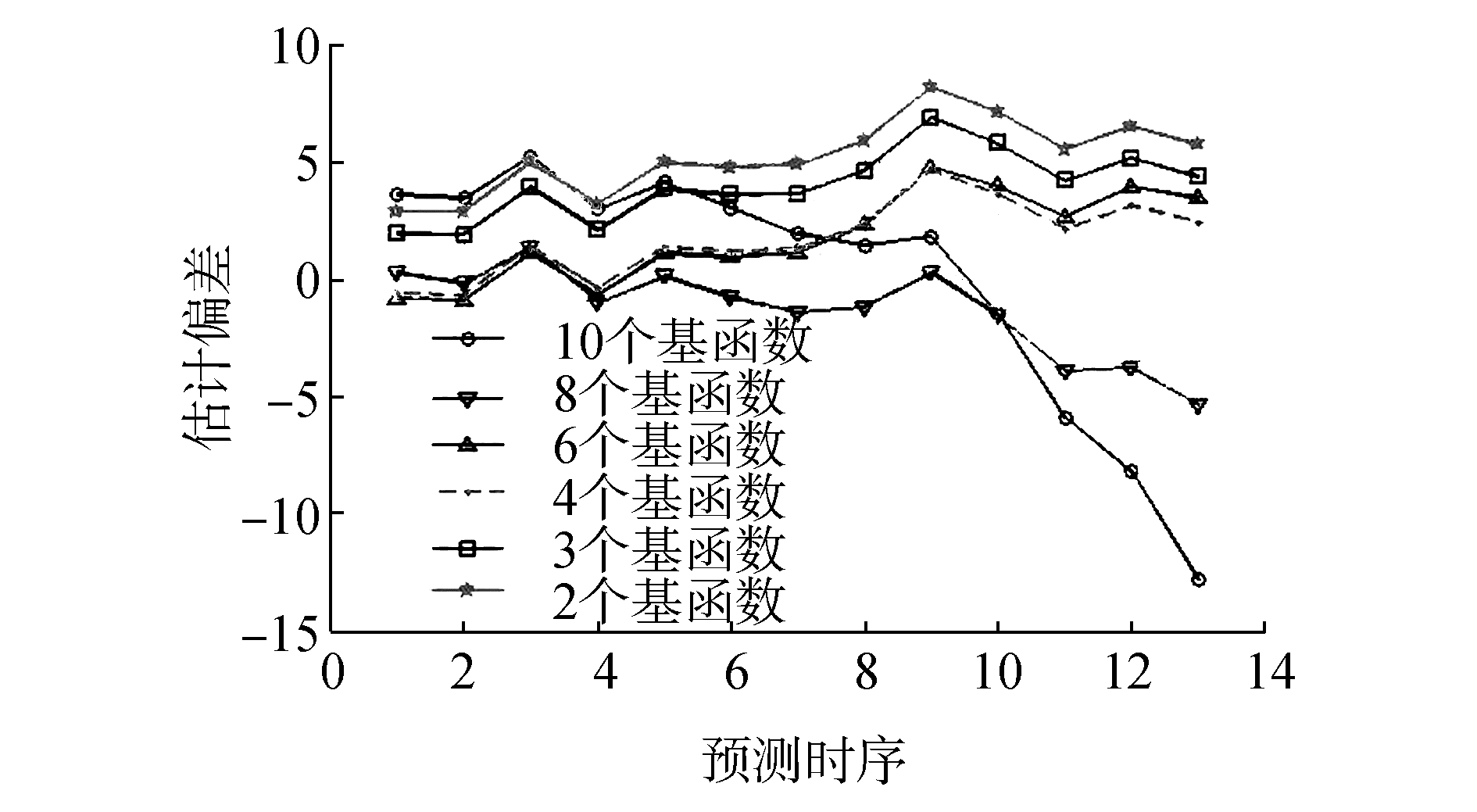
在傅里叶时间基函数下, 时间基展开维数的大小对预测的影响不仅有计算时间复杂度, 而且也体现在预测偏差上。图 6展示的是在不同傅里叶时间基函数下的估计偏差, 可以看出, 基时间展开维数为4~6的TVAR模型预测能较好地反映真实数据的变化趋势, 且预测误差也较小。因此本文选择傅里叶基时间函数, 基维数为4。
|
Download:
|
| 图 6 傅里叶时间基展开维数对预测偏差的曲线 | |
同上方法, 分别建立TVAR(p)的X和Y方向的数据模型, 因靶坐标在大地坐标系下的高程, 结合高程153个TVAR(3)模型, 最后计算再经过18个采样点时间到达靶平面, 将这18个采样点时间代入到X、Y坐标的TVAR模型中, 最后模型估算出XY的坐标。这次外场试验共打靶5次, 其弹坑经卫星定位测量, 和模型估计弹落点的误差如表 1所示。
|
|
表 1 模型估计弹落和实际测量值的误差 |
本文主要针对无线定位弹载炮弹在末段定位不准或信号丢失的情况, 1)研究了TVAR模型在炮弹弹落点预测的应用, 对于时变参数的估计采用了递推最小二乘法进行估计, 递推最小二乘在计算量不会随着时间推移增大, 而且占用存储空间少, 无需求逆, 适合时变参数估计; 2)通过对步长为13的时序进行傅里叶和多项式时间基函数以及AR模型的预测估计偏差, 采用傅里叶时间基函数的TVAR模型能很好地跟踪信号的变化趋势; 3)根据所建立TVAR模型估算炮弹与靶面相交的时序时刻, 代入XY的TVAR模型预测靶面坐标的炮弹落点X、Y坐标; 4)接下来会进一步展开时间基函数的研究, 确定扰动量化指标。
| [1] |
贺明科, 朱炬波, 周海银, 等. 弹道导弹落点的外推方法[J]. 战术导弹技术, 2002(5): 1-5. DOI:10.3969/j.issn.1009-1300.2002.05.001 ( 0) 0)
|
| [2] |
NØRGAARD M, POULSEN N K, RAVN O. New developments in state estimation for nonlinear systems[J]. Automatica, 2000, 36(11): 1627-1628. DOI:10.1016/S0005-1098(00)00089-3 ( 0) 0)
|
| [3] |
高伟伟, 申丽然. 时变AR模型阶数确定与系数估计的方法[J]. 应用科技, 2010, 37(11): 30-34. DOI:10.3969/j.issn.1009-671X.2010.11.008 ( 0) 0)
|
| [4] |
孔雁凯, 关咏梅, 郭涛, 等. 基于无线传感器网络的炮弹落点定位技术的研究[J]. 传感技术学报, 2015, 28(8): 1201-1206. DOI:10.3969/j.issn.1004-1699.2015.08.017 ( 0) 0)
|
| [5] |
王国锋, 罗志高, 秦旭达, 等. 非平稳信号的时变自回归建模及其在轴承故障诊断中的应用[J]. 天津大学学报, 2008, 41(5): 558-562. DOI:10.3969/j.issn.0493-2137.2008.05.009 ( 0) 0)
|
| [6] |
王莉娜, 姜相夺, 芦玉华. 基于时变自回归模型的非平稳数据预测方法研究[J]. 微型电脑应用, 2014, 30(8): 34-36. DOI:10.3969/j.issn.1007-757X.2014.08.010 ( 0) 0)
|
| [7] |
陈慧, 张龙, 熊国良, 等. 基于TVAR的非平稳工况转子故障诊断技术研究[J]. 华东交通大学学报, 2006, 23(5): 115-118, 132. DOI:10.3969/j.issn.1005-0523.2006.05.032 ( 0) 0)
|
| [8] |
王正明, 易东云. 测量数据建模与参数估计[M]. 长沙: 国防科技大学出版社, 1996.
( 0) 0)
|
| [9] |
芦玉华, 王仲生, 姜洪开. 基于改进时变自回归模型的滚动轴承故障诊断[J]. 振动与冲击, 2011, 30(12): 74-77, 107. DOI:10.3969/j.issn.1000-3835.2011.12.015 ( 0) 0)
|
| [10] |
陈伟. 自回归模型估计理论及其在变形监测数据处理中的应用[D]. 武汉: 武汉大学, 2013: 27-41.
( 0) 0)
|
| [11] |
丁胡进, 张二刚. 多项式曲线拟合与AR模型在沉降预测中的应用[J]. 北京测绘, 2012(6): 83-87. DOI:10.3969/j.issn.1007-3000.2012.06.022 ( 0) 0)
|
| [12] |
BEKIROS S. Forecasting with a state space time-varying parameter VAR model:evidence from the Euro area[J]. Economic modelling, 2014, 38: 619-626. DOI:10.1016/j.econmod.2014.02.015 ( 0) 0)
|
| [13] |
张龙, 熊国良, 柳和生, 等. 时变参数模型及其在非平稳振动分析中的应用[J]. 振动与冲击, 2006, 25(6): 49-53. DOI:10.3969/j.issn.1000-3835.2006.06.013 ( 0) 0)
|
| [14] |
李丽. 靶场弹落点无线定位系统的研究[D]. 太原: 中北大学, 2009: 5-9. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1509560
( 0) 0)
|
| [15] |
任妘梅. 基于无线传感器网络定位技术的研究[D]. 西安: 西安电子科技大学, 2013: 4-7. https://wenku.baidu.com/view/1a0fbe0e31126edb6f1a1046.html
( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


