随着人工智能技术的发展,自主机器人领域逐渐成为一个研究的热点方向[1]。其中机器人自定位能力是服务型机器人实现协同协作、运动规划和控制决策等任务的基础,所以高精度、鲁棒性的定位方法一直是机器人领域重要的研究问题[2]。
目前移动机器人领域广泛应用的定位传感器包括里程计、激光雷达、超声传感器和视觉传感器等,也常利用RFID、GPS和WLAN等方式进行定位[3]。其中里程计是一种常用的相对定位传感器,具有累计误差,普遍被用作辅助定位手段;超声传感器具有成本低廉、硬件容易实现且技术较成熟等优点,但需要环境中覆盖大量的信标;激光传感器的分辨率低且信息量少,在动态环境中的噪声大,而且价格昂贵[4];借助RFID的定位方法多用于室内,需要在环境中设置大量的电子路标;GPS普遍应用于室外定位, 在相对封闭的空间并不具备定位能力[5];WLAN的定位范围较大,但易受电磁干扰且存在探索盲区,实际应用时的鲁棒性较差[6];而全景视觉具有获取的信息量大、价格低廉等优势,被广泛应用于机器人定位[7-8]。
全景视觉传感器具有探测范围广、获取信息量大等优点,恰好能够为自主移动机器人提供丰富的环境信息。Shinichi等[9]利用2个双曲面全景摄像机构成水平基线的全景立体视觉系统,此系统安装在移动机器人上,利用运动与重建方法估计机器人的运动参数,并由光路跟踪方法对提取的特征点进行立体匹配,获得空间景物特征点的三维信息,但自主定位算法不够完备。在基于全景视觉的机器人定位研究中,文献[10]提出了基于全景视觉的即时定位与地图构建(simultaneous localization and mapping, SLAM)算法,实现了全局范围的定位,但该算法鲁棒性与实时性不足。而采用人工神经网络的视觉定位方法,虽然能够提高定位的智能化,但深度神经网络训练困难[11]。综上,将全景视觉应用在机器人定位还需进一步研究。
文中提出一种基于极大似然估计算法的全景立体视觉机器人自主定位方法。将常应用于无线传感器网络的定位方式[12-15]独特地应用到全景立体视觉系统,并结合双目全景视觉的特点进行一系列改进,设计了完整的机器人定位算法,并进行了大量的实验,结果表明该方法具有足够的精度和可靠性,能够应用于服务型机器人的室内定位任务。
1 极大似然估计法为实现在多人工路标环境下的机器人自主定位,采用极大似然估计算法。设测量值Z在估计量X下的条件概率密度为f(Z/X),取使函数∏kf(Z/X)达到最大值的参数值X作为X估计值,即
| $ \prod\nolimits_k {f\left( {\frac{{Z\left( k \right)}}{{\bar X}}} \right)} = \max \prod\nolimits_k {f\left( {\frac{{Z\left( i \right)}}{X}} \right)} $ | (1) |
将式(1)视为X的函数,设似然函数为L(Zk, X),若L(Zk, X)在X达到最大值,则X是X的极大似然估计。所以求估计量的极大似然估计,转化为求似然函数L的最大值问题:
| $ \begin{array}{*{20}{c}} {L = L\left( {{X^k},X} \right) = L\left( {Z\left( 1 \right),Z\left( 2 \right), \cdots ,Z\left( k \right),X} \right) = }\\ {\prod\nolimits_k {f\left( {\frac{{Z\left( i \right)}}{X}} \right)} } \end{array} $ |
因ln(n)和L同时达到最大值,所以求ln(n)的最大值即可。在一般情况下,设行向量X =(x1, x2, …, xn),令ln(L)在最大值点X=(X1, X2, …, Xn的一阶偏导数为零,求解该方程组:
| $ \frac{\partial }{{\partial {x_1}}}\ln \left( L \right) = 0,\frac{\partial }{{\partial {x_2}}}\ln \left( L \right) = 0, \cdots ,\frac{\partial }{{\partial {x_n}}}\ln \left( L \right) = 0 $ | (2) |
式(2)的解X即为f(Z/X)中参数X的极大似然估计量。如果函数u=u(X)具有单值反函数X=X(u),则u(X)也是u(X)的极大似然估计向量。
在计算时需要已知测量值Z在估计值X下的条件概率分布,在工程应用时常假设为正态分布。
2 机器人定位算法 2.1 三边定位算法在机器人视觉路标方面,文中的定位算法采用预先设置的人工路标,通过双目全景视觉系统实现自主定位。假设环境中存在的3个人工路标分别记为M1、M2和M3,坐标分别为(x1, y1)、(x2, y2)和(x3, y3),与机器人R(x, y)的距离分别为d1、d2和d3,则机器人的坐标可采用三边定位算法计算,几何关系方程组为
| $ \left\{ \begin{array}{l} {\left( {{x_1} - x} \right)^2} + {\left( {{y_1} - y} \right)^2} = d_1^2\\ {\left( {{x_2} - x} \right)^2} + {\left( {{y_2} - y} \right)^2} = d_2^2\\ {\left( {{x_3} - x} \right)^2} + {\left( {{y_3} - y} \right)^2} = d_3^2 \end{array} \right. $ |
各方程分别减去最后一个方程得
| $ \left\{ \begin{array}{l} x_1^2 - x_3^2 - 2\left( {{x_1} - {x_3}} \right)x + y_1^2 - y_3^2 - 2\left( {{y_1} - {y_3}} \right)y = d_1^2 - d_3^2\\ x_2^2 - x_3^2 - 2\left( {{x_2} - {x_3}} \right)x + y_2^2 - y_3^2 - 2\left( {{y_2} - {y_3}} \right)y = d_2^2 - d_3^2 \end{array} \right. $ |
将上式线性方程表示为AX=b,参数定义如式(3):
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {2\left( {{x_1} - {x_3}} \right)}&{2\left( {{y_1} - {y_3}} \right)}\\ {2\left( {{x_2} - {x_3}} \right)}&{2\left( {{y_2} - {y_3}} \right)} \end{array}} \right]\\ \mathit{\boldsymbol{b}} = \left[ \begin{array}{l} x_1^2 - x_3^2 + y_1^2 - y_3^2 + d_3^2 - d_1^2\\ x_2^2 - x_3^2 + y_2^2 - y_3^2 + d_3^2 - d_2^2 \end{array} \right]\\ \mathit{\boldsymbol{X = }}\left[ {\begin{array}{*{20}{c}} x\\ y \end{array}} \right] \end{array} \right. $ | (3) |
当|A|=4(x1-x3)(y2-y3)-4(x2-x3)· (y1-y3)≠0时,设
| $ \left\{ \begin{array}{l} K = 2\left( {{x_1} - {x_3}} \right)\left( {{y_2} - {y_3}} \right) - 2\left( {{x_2} - {x_3}} \right)\left( {{y_1} - {y_3}} \right)\\ {K_1} = x_1^2 - x_3^2 + y_1^2 - y_3^2 + d_3^2 - d_1^2\\ {K_2} = x_2^2 - x_3^2 + y_2^2 - y_3^2 + d_3^2 - d_2^2 \end{array} \right. $ |
计算逆矩阵A-1为
| $ {\mathit{\boldsymbol{A}}^{ - 1}} = \frac{1}{{\left| \mathit{\boldsymbol{A}} \right|}}{\mathit{\boldsymbol{A}}^ * } = \frac{1}{{\left| \mathit{\boldsymbol{A}} \right|}}\left[ {\begin{array}{*{20}{c}} {2\left( {{y_2} - {y_3}} \right)}&{2\left( {{y_3} - {y_1}} \right)}\\ {2\left( {{x_3} - {x_2}} \right)}&{2\left( {{x_1} - {x_3}} \right)} \end{array}} \right] $ |
则机器人坐标为
| $ \left[ {\begin{array}{*{20}{c}} x\\ y \end{array}} \right] = {\mathit{\boldsymbol{A}}^{ - 1}}\mathit{\boldsymbol{b = }}\left[ \begin{array}{l} \frac{{{K_1}}}{K}\left( {{y_2} - {y_3}} \right) + \frac{{{K_2}}}{K}\left( {{y_3} - {y_1}} \right)\\ \frac{{{K_1}}}{K}\left( {{y_3} - {y_2}} \right) + \frac{{{K_2}}}{K}\left( {{y_1} - {y_3}} \right) \end{array} \right] $ |
在三边定位算法基础上进行推广,当机器人移动范围扩大时,当路标数较少,常常会因为视角、遮挡等情况,识别不到足够的路标,无法完成自主定位任务,所以增加路标冗余度,有利于提高定位的鲁棒性。进一步讨论四路标定位算法,假设4个路标的坐标分别为(x1, y1)、(x2, y2)、(x3, y3)和(x4, y4),与移动机器人的距离分别为d1、d2、d3和d4,几何方程式为
| $ \left\{ \begin{array}{l} {\left( {{x_1} - x} \right)^2} + {\left( {{y_1} - y} \right)^2} = d_1^2\\ {\left. {{x_2} - x} \right)^2} + {\left( {{y_2} - y} \right)^2} = d_2^2\\ {\left( {{x_3} - x} \right)^2} + {\left( {{y_3} - y} \right)^2} = d_3^2\\ {\left( {{x_4} - x} \right)^2} + {\left( {{y_4} - y} \right)^2} = d_4^2 \end{array} \right. $ |
采用极大似然估计法,同理化简方程组得:
| $ \left\{ \begin{array}{l} x_1^2 - x_4^2 - 2\left( {{x_1} - {x_4}} \right)x + y_1^2 - y_4^2 - 2\left( {{y_1} - {y_4}} \right)y = d_1^2 - d_4^2\\ x_2^2 - x_4^2 - 2\left( {{x_2} - {x_4}} \right)x + y_2^2 - y_4^2 - 2\left( {{y_2} - {y_4}} \right)y = d_2^2 - d_4^2\\ x_3^2 - x_4^2 - 2\left( {{x_3} - {x_4}} \right)x + y_3^2 - y_4^2 - 2\left( {{y_3} - {y_4}} \right)y = d_3^2 - d_4^2 \end{array} \right. $ |
上式线性方程表示为AX=b,此时参数矩阵为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {2\left( {{x_1} - {x_4}} \right)}&{2\left( {{y_1} - {y_4}} \right)}\\ {2\left( {{x_2} - {x_4}} \right)}&{2\left( {{y_2} - {y_4}} \right)}\\ {2\left( {{x_3} - {x_4}} \right)}&{2\left( {{y_3} - {y_4}} \right)} \end{array}} \right]\\ \mathit{\boldsymbol{b}} = \left[ \begin{array}{l} x_1^2 - x_4^2 + y_1^2 - y_4^2 + d_4^2 - d_1^2\\ x_2^2 - x_4^2 + y_2^2 - y_4^2 + d_4^2 - d_2^2\\ x_3^2 - x_4^2 + y_3^2 - y_4^2 + d_4^2 - d_3^2 \end{array} \right]\\ \mathit{\boldsymbol{X = }}\left[ {\begin{array}{*{20}{c}} x\\ y \end{array}} \right] \end{array} \right. $ |
此时A为非奇异矩阵,方程数大于未知数的数目,使用最小二乘估计方法,计算移动机器人R的坐标为
| $ \bar X = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{b}} $ |
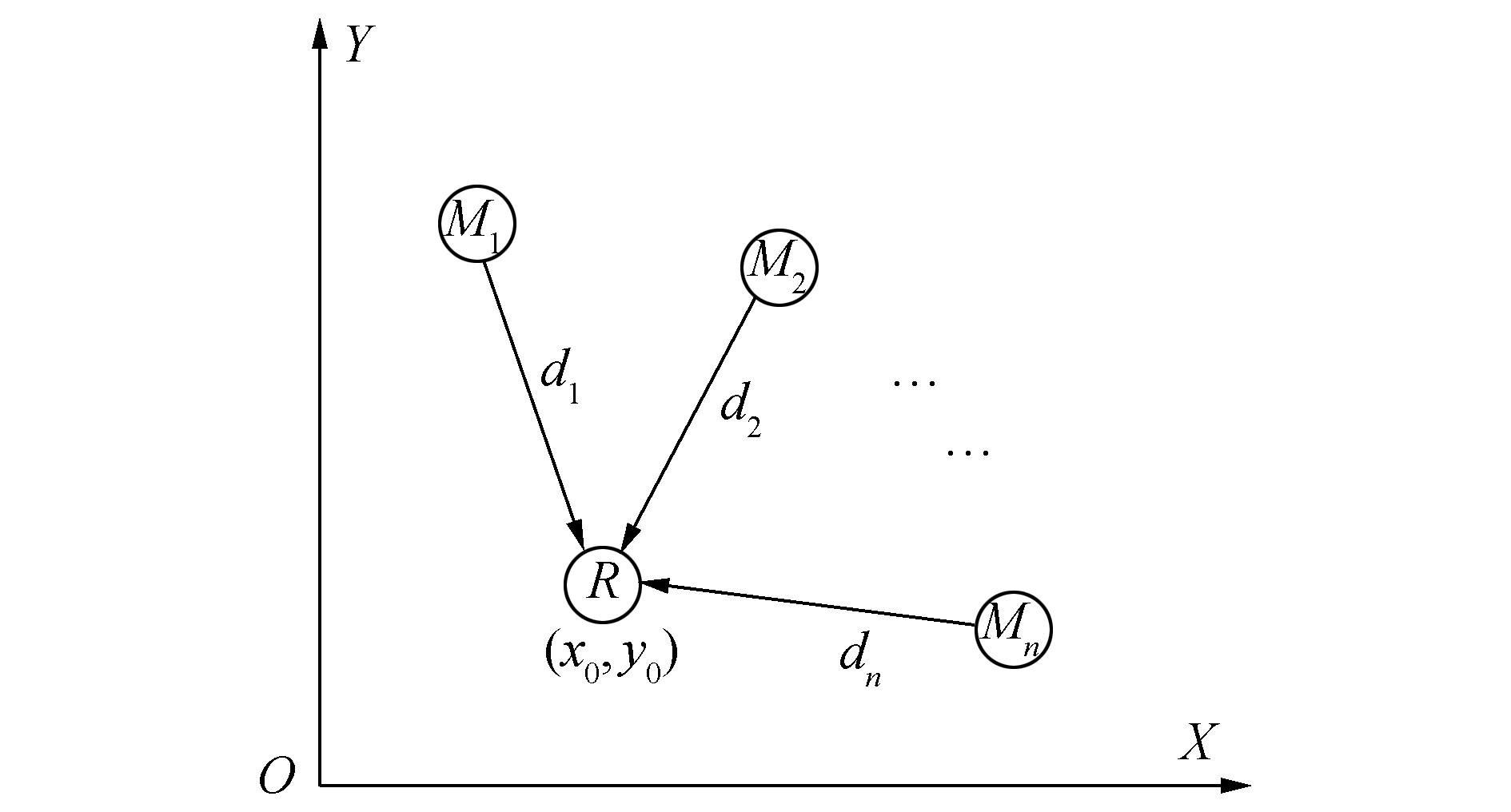
将多路标定位算法进一步推广,极大似然估计定位法如图 1所示,已知n个人工路标的坐标分别为(x1, y1)、(x2, y2)、(x3, y3)、…、(xn, yn),与机器人R的距离分别为d1、d2、d3、…、dn。
|
图 1 极大似然估计定位法 |
假设机器人的坐标为R(x, y),几何关系方程组为
| $ \left\{ {\begin{array}{*{20}{c}} {{{\left( {{x_1} - x} \right)}^2} + {{\left( {{y_1} - y} \right)}^2} = d_1^2}\\ \vdots \\ {{{\left( {{x_n} - x} \right)}^2} + {{\left( {{y_n} - y} \right)}^2} = d_1^2} \end{array}} \right. $ |
各方程分别减去最后一个方程得
| $ \left\{ \begin{array}{l} x_1^2 - x_n^2 - 2\left( {{x_1} - {x_n}} \right)x + y_1^2 - y_n^2 - 2\left( {{y_1} - {y_n}} \right)y = d_1^2 - d_n^2\\ x_2^2 - x_n^2 - 2\left( {{x_2} - {x_n}} \right)x + y_2^2 - y_n^2 - 2\left( {{y_2} - {y_n}} \right)y = d_2^2 - d_n^2\\ \; \vdots \\ x_{n - 1}^2 - x_n^2 - 2\left( {{x_{n - 1}} - {x_n}} \right)x + y_{n - 1}^2 - y_n^2 - 2\left( {{y_{n - 1}} - {y_n}} \right)y = d_{n - 1}^2 - d_n^2 \end{array} \right. $ |
上式线性方程表示AX=b,其中参数矩阵为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {2\left( {{x_1} - {x_n}} \right)}&{2\left( {{y_1} - {y_n}} \right)}\\ \vdots&\vdots \\ {2\left( {{x_{n - 1}} - {x_n}} \right)}&{2\left( {{y_{n - 1}} - {y_n}} \right)} \end{array}} \right]\\ \mathit{\boldsymbol{b}} = \left[ {\begin{array}{*{20}{c}} {x_1^2 - x_n^2 + y_1^2 - y_n^2 - d_1^2 + d_n^2}\\ \vdots \\ {x_{n - 1}^2 - x_n^2 + y_{n - 1}^2 - y_n^2 - d_{n - 1}^2 + d_n^2} \end{array}} \right]\\ \mathit{\boldsymbol{X = }}\left[ {\begin{array}{*{20}{c}} x\\ y \end{array}} \right] \end{array} \right. $ |
使用最小二乘估计估计法可计算到机器人坐标,设测量值Z与估计值满足关系:
| $ \mathit{\boldsymbol{Z}}\left( j \right) = \mathit{\boldsymbol{h}}\left( {j,x} \right) + \mathit{\boldsymbol{V}}\left( j \right),j = 1,2, \cdots ,n $ |
式中V(j)为测量噪声(设每个V(j)在J中的加权和值相等)。在第K时刻的最小二乘估计,设使得前K次误差的平方和达到最小的参数X值定义为X(K)。当h(j, x)= H(j)X,其中H(i)为m×n阶矩阵,令
| $ \mathit{\boldsymbol{J}}\left( K \right) = \sum\limits_{j = 1}^K {{{\left[ {\mathit{\boldsymbol{Z}}\left( j \right) - \mathit{\boldsymbol{H}}\left( j \right)\mathit{\boldsymbol{X}}} \right]}^{\rm{T}}}\left[ {\mathit{\boldsymbol{Z}}\left( j \right) - \mathit{\boldsymbol{H}}\left( j \right)\mathit{\boldsymbol{X}}} \right]} $ |
为了得到X,对X求导,考虑到XTHTZ=ZTHX,得到
| $ \begin{array}{*{20}{c}} {\frac{{\partial \mathit{\boldsymbol{J}}}}{{\partial \mathit{\boldsymbol{\bar X}}}} = \frac{{\left[ {{\mathit{\boldsymbol{Z}}^{\rm{T}}}\mathit{\boldsymbol{Z}} - 2{{\mathit{\boldsymbol{\bar X}}}^{\rm{T}}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{Z}} + {{\mathit{\boldsymbol{\bar X}}}^{\rm{T}}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H\bar X}}} \right]}}{{\partial \mathit{\boldsymbol{\bar X}}}} = }\\ {2{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H\bar X}} - 2{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{Z}}}=0 \end{array} $ |
进一步得到
| $ \mathit{\boldsymbol{\bar X}}\left( K \right) = {\left[ {{{\left( {{\mathit{\boldsymbol{H}}^K}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{H}}^K}} \right)} \right]^{ - 1}}{\left( {{\mathit{\boldsymbol{H}}^K}} \right)^{\rm{T}}}{\mathit{\boldsymbol{Z}}^K} $ |
其中(HK)-1=H(1) H(2) … H(k), (ZK)-1=Z(1) Z(2)…Z(k)。
当A为非奇异矩阵,且路标数大于3时,几何方程组为方程数大于未知数的数目的超定方程组,使用标准的最小二乘估计方法求解
| $ \mathit{\boldsymbol{J}} = {\left[ {\mathit{\boldsymbol{b}} - \mathit{\boldsymbol{A\bar X}}} \right]^{\rm{T}}}\left[ {\mathit{\boldsymbol{b}} - \mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{\bar X}}}^{\rm{T}}}} \right] = \left[ {{\mathit{\boldsymbol{b}}^{\rm{T}}} - {{\mathit{\boldsymbol{\bar X}}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}} \right]\left[ {\mathit{\boldsymbol{b}} - \mathit{\boldsymbol{A\bar X}}} \right] $ |
为了得到移动机器人的坐标X,将上式对X求导,由XTATb=bTAX可得
| $ \begin{array}{*{20}{c}} {\frac{{\partial J}}{{\partial \mathit{\boldsymbol{\bar X}}}} = \frac{{\left[ {{\mathit{\boldsymbol{b}}^{\rm{T}}}\mathit{\boldsymbol{b}} - 2{{\mathit{\boldsymbol{\bar X}}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{b}} + {{\mathit{\boldsymbol{\bar X}}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A\bar X}}} \right]}}{{\partial \mathit{\boldsymbol{\bar X}}}} = }\\ { - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{b}} + 2{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A\bar X}} = 0} \end{array} $ |
计算机器人R的坐标为
| $ \mathit{\boldsymbol{\bar X}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{b}} $ |
当外界干扰而引起的测量误差不具相关性时,最小二乘估计在参数估计中具有很好的无偏性、有效性和一致性,因此是非常优良的一种参数估计方法。
3 全景视觉深度测量算法采用全景立体视觉系统获取路标与机器人的距离。依据折反射式全景成像系统的旋转不变性的特点,选取研究平面为光轴截面,建立坐标系如图 2所示。

|
图 2 全景立体成像模型 |
双曲面镜的上支顶点为坐标原点,水平与竖直分别为X和Y轴方向。设双曲面镜实轴、虚轴和焦距长度分别为a、b和c,则双曲面镜曲线方程为(y-c)2/a2-x2/b2=1。利用SURF(speeded-up robust features)特征匹配算法,识别出路标在全景图像中的位置。任意选取一个路标研究,设路标中心点坐标为A1(x1, y1)。忽略安装精度的偏差情况下,全景图像的几何中心即为光心位置G(x0, y0),则图像中路标A1距全景图像中心P0的距离r=
| $ \left\{ \begin{array}{l} m = \frac{{{b^2}fc{r_1} + a{r_1}{b^2}\sqrt {{f^2} + r_1^2} }}{{{b^2}{f^2} - {a^2}r_1^2}}\\ n = \frac{{{b^2}{f^2}c + a{b^2}f\sqrt {{f^2} + r_1^2} }}{{{b^2}{f^2} - {a^2}r_1^2}} \end{array} \right. $ |
同向折反射式垂直双目全景系统测距原理如图 2所示,入射光线的斜率为k=(n-2c)/m。
假设上下全景系统的入射光线与双曲面镜的交点分别为Q1(m1, n1)和Q2(m2, n2),由斜率公式求解两入射光线的斜率,计算上下全景相机的入射光线方程为
| $ \left\{ \begin{array}{l} y = \left( {{n_1} - 2c} \right)/{m_1}x + 2c\\ y = \left( {{n_2} - 2c} \right)/{m_2}x + 2c - L \end{array} \right. $ |
联立入射光线方程组,可解算移动机器人与路标之间的水平距离d,距离求解公式为
| $ d = \left| x \right| = \left| {\frac{{{m_1}{m_2}L}}{{{m_1}\left( {{n_2} - 2c} \right) - {m_2}\left( {{n_1} - 2c} \right)}}} \right| $ |
文中使用全景立体视觉系统如图 3所示。两个单视点全景摄像机垂直安装,摄像机均使用由实验室自主加工制造的高精度双曲面反射镜和POINT GREY 1394相机组合而成。精密加工的立体支撑结构件可保证上下全景摄像机具有较高的初始同轴安装精度。

|
图 3 全景立体系统实物 |
垂直基线安装间距为332 mm,同时摄像机安装底座具备三自由度调节功能,保证全景摄像机单视点安装要求。反射镜及相机参数如表 1所示。
|
|
表 1 全景摄像机参数 |
在机器人运动环境(12 m×9 m)中安放3个人工路标,高度为2.1 m,相邻间隔为2.5 m。机器人搭载的全景立体视觉系统安装的最大高度为1.2 m。通过双目全景视觉系统进行了多次三边定位实验,随机选取一次实验中采集的一组全景图像库数据,如图 4所示。

|
图 4 全景图像库序列 |
由于机器人在不同位置,所获取的全景图像的环境信息均不相同,而上下全景图像仅存在的深度信息的视差,所以为了简明描述,在图 4中展示为上面全景相机采集的图像库序列。图 5为实验环境的鸟瞰图,为不失一般性,所选的8组位置等概率随机分布在机器人可移动的区域中。利用三边定位算法,进行移动机器人的自主定位实验,机器人实际位置点坐标与测量位置结果对比见表 2。

|
图 5 机器人实验位置 |
|
|
表 2 定位数据 |
经过多次定位实验,结果表明三边定位平均测量误差为2.7 cm,标准差为8.4 cm,最大误差小于11.5 cm,能够满足室内服务型机器人的定位精度要求。
4.3 路标序列定位实验当机器人运行在大范围环境时,精简路标已经难以满足可靠定位的需求,通过增加路标的数量可拓展定位范围,也可提高定位精度。在室内环境中安放2~10个路标,利用极大似然估计定位算法进行实验,机器人自定位的平均误差如图 6所示。

|
图 6 机器人定位的平均误差 |
基于3个路标实现的三边定位算法能够实现较为精准的定位,随着路标的增加,定位逐渐提高。但是依据极大似然估计定位算法的原理,随着路标数目的增加,机器人定位的实时性逐渐下降,在简化SURF算法识别路标过程中所耗的时间也逐渐增加。图 7为不同路标数情况下的一次定位循环所耗费的时间,当定位路标数为2~4个时能够实现周期在100 ms以内的单循环,满足定位的实时性需求。

|
图 7 机器人定位的实时性 |
1) 文中所提出的基于极大似然估计算法的全景立体视觉机器人自主定位方法, 能够高效地完成了移动机器人在复杂室内环境下的定位任务。
2) 建立了双目全景系统深度探测的模型,利用三边定位算法实现机器人定位,并推广提出了基于多路标的极大似然定位方法,设计完备的定位算法,实现了机器人的绝对坐标解算。
3) 该方法能够应用于大范围环境的全局定位。进行了多次定位试验,测得算法平均定位误差2.7 cm,标准差为8.4 cm,最大误差小于11.5 cm,能够满足服务型机器人应用需求。但由于实验平台移动机器人的处理器配置局限,运行实时性有待优化,在硬件性能提升和软件算法实时性加速方面还需要进一步研究。
| [1] |
LAN Gongwen, WANG Jianchun, CHEN Weidong. An improved indoor localization system for mobile robots based on landmarks on the ceiling[C]//Proceedings of IEEE International Conference on Robotics and Biomimetics.Qingdao:IEEE, 2016:1395-1400.
( 0) 0)
|
| [2] |
MARTÍNEZ-BARBERÁH, HERRERO-PÉREZ D. Autonomous navigation of an automated guided vehicle in industrial environments[J]. Robotics and computer-integrated manufacturing, 2010, 26(4): 296-311. DOI:10.1016/j.rcim.2009.10.003 ( 0) 0)
|
| [3] |
BOCCADORO M, MARTINELLI F, PAGNOTTELLI S. Constrained and quantized Kalman filtering for an RFID robot localization problem[J]. Autonomous robots, 2010, 29(3/4): 235-251. ( 0) 0)
|
| [4] |
ZHOU Bo, DAI Xianzhong, HAN Jianda. Real-time 3D outdoor environment modeling for mobile robot with a laser scanner[J]. Robot, 2012, 34(3): 321-328. DOI:10.3724/SP.J.1218.2012.00321 ( 0) 0)
|
| [5] |
VINCENT R, LIMKETKAI B, ERIKSEN M. Comparison of indoor robot localization techniques in the absence of GPS[C]//Proceedings of the SPIE 7664, Detection and Sensing of Mines, Explosive Objects, and Obscured Targets XV.Orlando, Florida, USA, 2010, 7664:76641Z.
( 0) 0)
|
| [6] |
BENJAMIN B, ERINC G, CARPIN S. Real-time WiFilocalization of heterogeneous robot teams using an online random forest[J]. Autonomous robots, 2015, 39(2): 155-167. DOI:10.1007/s10514-015-9432-5 ( 0) 0)
|
| [7] |
高云峰, 周伦, 吕明睿, 等. 自主移动机器人室内定位方法研究综述[J]. 传感器与微系统, 2013, 32(12): 1-5, 9. DOI:10.3969/j.issn.1000-9787.2013.12.001 ( 0) 0)
|
| [8] |
LI Maohai, HONG Bingrong, CAI Zesu, et al. Novel indoor mobile robot navigation using monocular vision[J]. Engineering applications of artificial intelligence, 2012, 21(3): 485-497. ( 0) 0)
|
| [9] |
GOTO S, YAMASHITA A, KAWANISHI R, et al. 3D environment measurement using binocular stereo and motion stereo by mobile robot with omnidirectional stereo camera[C]//Proceedings of 2011 IEEE International Conference on Computer Vision Workshops. Barcelona, Spain, 2011:296-303.
( 0) 0)
|
| [10] |
VALIENTE D, GIL A, FERNÁNDEZ L, et al. A comparison of EKF and SGDapplied to a view-based SLAM approach with omnidirectional images[J]. Robotics and autonomous systems, 2014, 62(2): 108-119. DOI:10.1016/j.robot.2013.11.009 ( 0) 0)
|
| [11] |
BESSA J A, BARROSO D A, DA ROCHA NETO A R, et al. Global location of mobile robots using artificial neural networks in omnidirectional images[J]. IEEE Latin America transactions, 2015, 13(10): 3405-3414. DOI:10.1109/TLA.2015.7387248 ( 0) 0)
|
| [12] |
钟丽鸿, 胡成全, 金京姬. 基于RSSI极大似然估计定位算法的分析与实现[J]. 吉林大学学报:理学版, 2014, 52(3): 556-560. ( 0) 0)
|
| [13] |
卢先领, 夏文瑞. 基于最大似然估计的加权质心定位算法[J]. 信息与控制, 2016, 45(5): 582-587. ( 0) 0)
|
| [14] |
CHEN Suisheng, LU Jiangang, LOU Xiaochun. Localization algorithm for wireless sensor networks based on MDS-MAP and nonlinear filtering[J]. Journal of Zhejiang university:engineering science, 2012, 46(5): 866-872. ( 0) 0)
|
| [15] |
ZHU Qidan, LIU Chuanjia, CAI Chengtao. A novel robot visual homing method based on SIFT features[J]. Sensors, 2015, 15(10): 26063-26084. DOI:10.3390/s151026063 ( 0) 0)
|
 2017, Vol. 44
2017, Vol. 44


