2. 西安交通大学 能源与动力工程学院,陕西 西安 710049;
3. 中国核动力研究设计院 核反应堆系统设计技术重点实验室,四川 成都 610041
2. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China;
3. National Key Laboratory on Reactor System Design Technology, Nuclear Power Institute of China, Chengdu 610041, China
超临界水堆(supercritical water-cooled reactor, SCWR)是第四代新型核能系统中唯一的水冷堆,具有热效率高、系统结构简单、安全性好、燃料利用率高等特点,在经济性、工程技术延续性以及可持续性等方面有着诸多优势[1]。加拿大超临界水冷堆(Canadian SCWR),是加拿大开发的一种SCWR,为压力管式反应堆,其堆芯压力为25 MPa,冷却剂入口温度为350 ℃,蒸汽温度为625 ℃,效率高达45%[2]。
Canadian SCWR用超临界水作冷却剂,冷却剂采用直接循环,其动态特征和性能响应与传统的坎杜堆有很大的不同,主要是由于超临界水物性特殊。Canadian SCWR有很大的功率/流量比,导致蒸汽温度对反应堆功率和系统压力的扰动具有高度敏感性[3];Canadian SCWR无蒸汽发生器,反应堆功率和汽轮机之间有很强的耦合性。基于这些原因,针对Canadian SCWR的控制系统设计比坎杜堆更困难。
在系统的建模过程中所采用的系统关系和模型参数与实际系统必然存在差别,同时由于Canadian SCWR系统的非线性较强,因而采用系统线性模型进行控制系统设计时不可避免地会引入一些不确定性因素,这些不确定性因素必然会影响控制系统的性能。文中首先对Canadian SCWR系统模型进行系统不确定性分析,确定了不确定性带宽。在不确定性条件下进行多变量鲁棒前馈/反馈控制器设计,通过和传统控制器所对应的系统响应的仿真对比,证明控制系统设计的合理性和正确性。
1 系统模型Canadian SCWR系统如图1所示,反应堆冷却剂由给水泵经压力容器上腔室送至堆芯,流经燃料通道后,吸收燃料棒所产生的热量而转变为蒸汽。蒸汽流经出口支路和出口接头进入汽轮机驱动叶轮热能转化为机械能。其中给水流量由给水泵控制,堆芯反应性由控制棒控制,蒸汽流量由汽轮机阀门开度控制。

|
图 1 加拿大SCWR系统的结构 |
Canadian SCWR堆芯热工水力模型利用质量、能量和动量守恒方程推导获得,其中冷却剂堆芯模型采用移动边界法以提高模型的计算精度;中子动力学模型采用带6组缓发中子的点堆模型,并考虑了慢化剂温度和燃料温度反应性反馈。该系统模型为三输入三输出系统动态模型,给水流量率、控制棒反应性和汽轮机阀门开度被视为系统输入,蒸汽温度、反应堆功率和主蒸汽压力被视为系统输出。
在系统动态性能分析和控制系统设计中,通常需要将所得到的非线性系统模型线性化,即在选定的工况点下模型的线性化过程,线性化后的模型采用传递函数矩阵表示。针对鲁棒控制设计的基本内容和目标,同时也为了尽可能好地代表系统的非线性特征,选取100%满功率(full power, FP)、80%FP和60%FP这3个线性化工况点。选择这个范围的功率工况作为运行工况有2个原因:1)对于超临界水冷堆,当反应堆功率较低水平时,冷却剂可能无法维持超临界态,此时反应堆热工水力特性和传热机理与超临界水有根本的不同,特别是当冷却剂刚好达到超临界态时,传热状态会发生显著的变化,超临界状态下所建立的反应堆模型在这种情况下并不适用。2)鲁棒控制系统设计系统不确定性量在一定范围之内,当不确定性量远远超出设计所能接受的量值时,鲁棒控制系统设计便无法成功。
2 系统不确定性分析系统建模过程中所采用的系统函数、模型参数、数学关系与所考察系统的实际情况并非完全一致,同时由于Canadian SCWR系统的非线性化程度高,在一种工况下所设计的控制系统往往只能在这种工况的一个小的邻域内适用,而无法在所有工况下都有良好的性态表现。为了解决性能控制设计和大范围控制系统设计问题,需进行系统不确定性分析,即先选择名义工况,其他工况与名义工况之间的相对差视为系统不确定性[4],在这种不确定性条件下设计控制系统,就能满足所有工况下系统的控制要求。基于这些系统不确定性因素的考虑,鲁棒控制被选用。所谓“鲁棒性”,是指控制系统在一定的参数(结构、大小)摄动(不确定性)下,维持某些性能的特性。根据对性能的不同定义,可分为稳定鲁棒性和性能鲁棒性[5]。以闭环系统的鲁棒性作为目标设计得到的固定控制器称为鲁棒控制器。
不确定性分析中,首先把不确定性系统分为名义部分和不确定性部分,并把不确定性部分设置为不确定性最大值(即不确定性带宽),然后构建输入端不确定性[5],其对应的数学表达式为
| ${\mathit{\boldsymbol{P}}_{{\rm{IM}}}}(s) = {\mathit{\boldsymbol{P}}_0}(s)(\mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{\varDelta }}_{{\rm{IM}}}}(s))$ |
其中
如图2所示,针对Canadian SCWR系统建模和模型分析过程,所考虑的不确定性有未建模不确定性、线性化不确定性和模型简化不确定性。
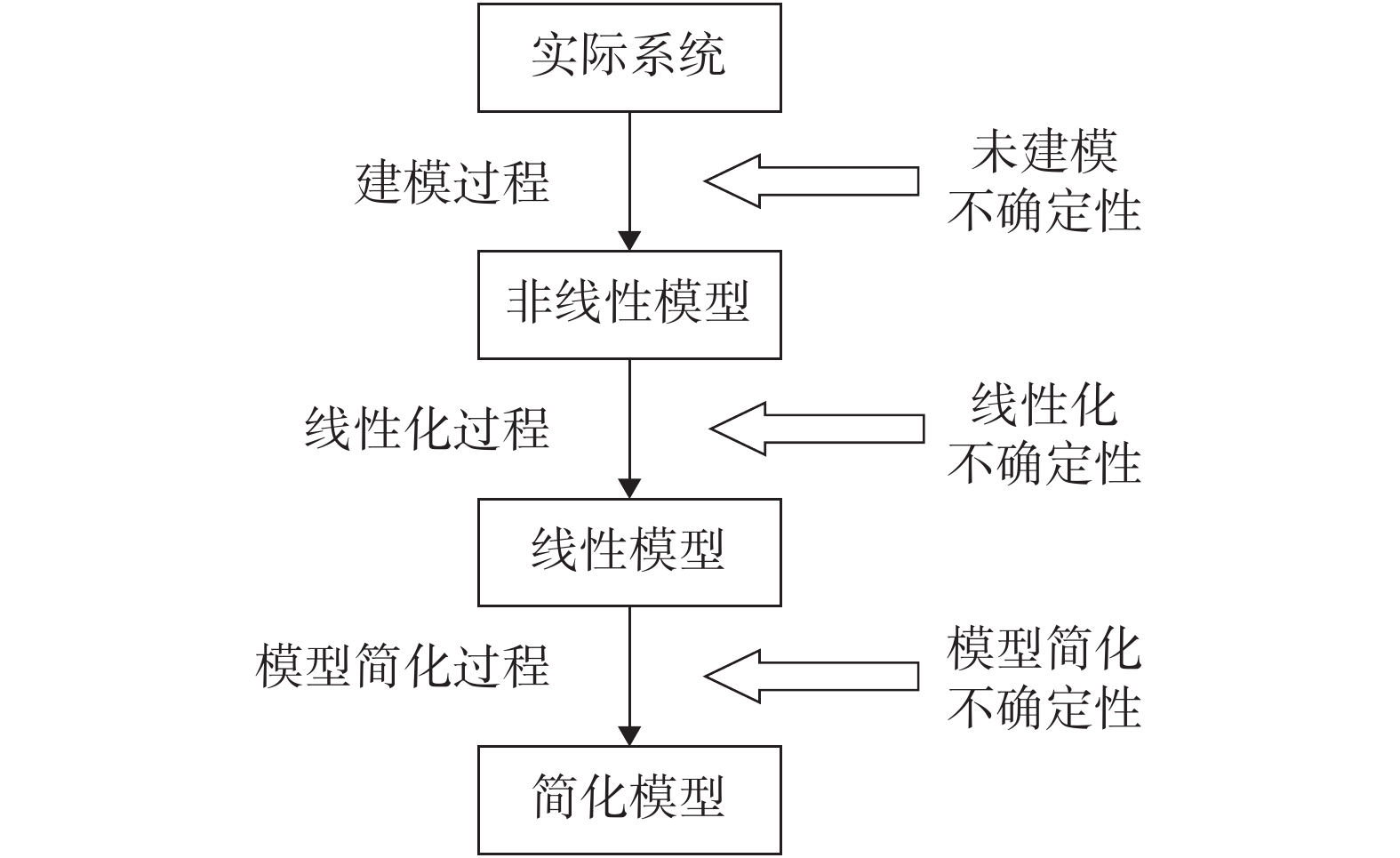
|
图 2 系统不确定性来源 |
系统运行所对应的数学方程式只是系统物理过程的一种近似表达,真实系统和系统非线性模型之间必然存在未能建模的部分,这种未能建模部分就是未建模不确定性,其量值通过计算系统实际运行数据与非线性模型之间的相对差来确定。系统未建模不确定性的定量化,基于对Canadian SCWR系统模型的详细仿真结果[3],最后通过分析频率曲线得到系统未建模不确定性带宽,其对应的矩阵形式为
| ${{\varDelta} _{{\rm{Unmodeled}}}}(s) = \left[ {\begin{array}{*{20}{c}}{\displaystyle\frac{{0.000\,\, 8(10s + 1)}}{{0.1s + 1}}} & 0 & 0 \\0 & {\displaystyle\frac{{0.000\,\, 8(10s + 1)}}{{0.1s + 1}}} & 0\\0 & 0 & {\displaystyle\frac{{0.000\,\, 8(10s + 1)}}{{0.1s + 1}}}\end{array}}\right]$ |
线性化不确定性即为非线性模型和线性模型之间的相对差。本工作所选取的线性化工况点分别是60%FP、80%FP和100%FP,名义工况选为80%FP工况,因而线性化不确定性来源有2个方面:系统60%FP工况下的线性模型与80%FP工况下的线性模型的相对差;系统100%FP工况下的线性模型与80%FP工况下的线性模型的相对差。图3为系统模型每个输入到每个输出间线性化不确定性函数图像。
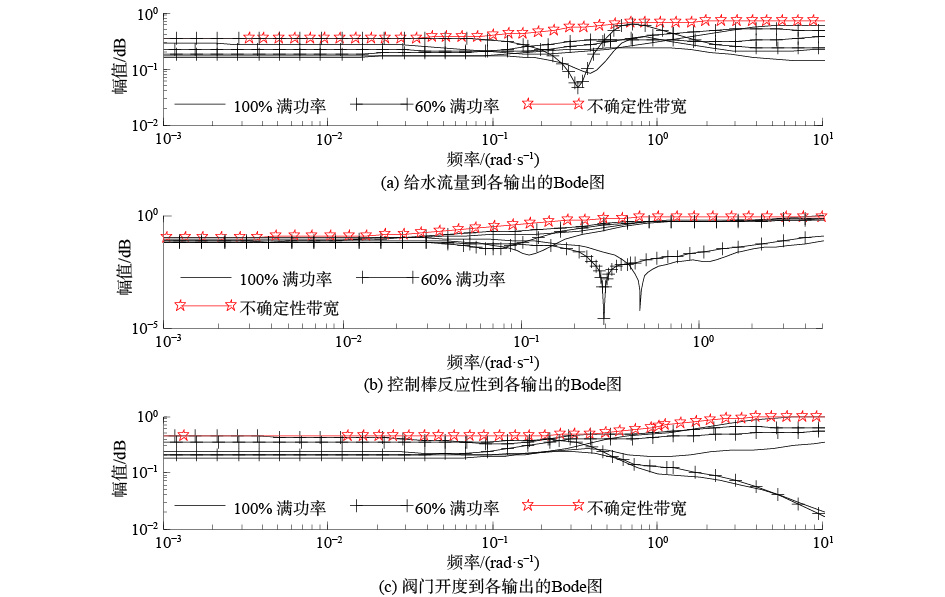
|
图 3 系统各输入到各输出之间的模型线性化不确定性的频率特性曲线 |
线性化不确定性带宽为
| ${\mathit{\boldsymbol{\varDelta }}_{{\rm{Linearization}}}}(s) = \left[ {\begin{array}{*{20}{c}}{\displaystyle\frac{{0.365({\rm{6}}s{\rm{ + 1}})}}{{{\rm{3}}s{\rm{ + 1}}}}} & 0 & 0\\[10pt]0 & {\displaystyle\frac{{{\rm{0}}{\rm{.8(}}s{\rm{ + 0}}{\rm{.025\,\,5)}}}}{{s{\rm{ + 0}}{\rm{.2}}}}} & 0\\[10pt]0 & 0 & {\displaystyle\frac{{{\rm{0}}{\rm{.435(1}}{\rm{.5}}s{\rm{ + 1)}}}}{{{\rm{0}}{\rm{.65}}s{\rm{ + 1}}}}}\end{array}} \right]$ |
模型简化不确定性是针对线性模型降阶简化过程中所引入的误差,其量化形式同线性化不确定性一样,其不确定性来源只有一方面,结果如图4所示,模型简化不确定性带宽为
| ${\mathit{\boldsymbol{\varDelta }}_{{\rm{Reduction}}}}(s) = \left[ {\begin{array}{*{20}{c}}{\displaystyle\frac{{0.000 \,\, 018(s{\rm{ + 0}}{\rm{.041}})}}{{s{\rm{ + 1}}}}} & 0 & 0 \\0 & {\displaystyle\frac{{{\rm{0}}{\rm{.000} \,\, } {\rm{002(}}s{\rm{ + 1)}}}}{{s{\rm{ + 2}}}}} & 0\\0 & 0 & {\displaystyle\frac{{{\rm{0}}{\rm{.000} \,\, } {\rm{3(}}s{\rm{ + 0}}{\rm{.04)}}}}{{s{\rm{ + 10}}}}}\end{array}} \right]$ |

|
图 4 系统各输入到各输出之间的模型简化不确定性的频率特性曲线 |
通过以上的计算可得到系统总的不确定性带宽
| $\left| {{\mathit{\boldsymbol{\varDelta }}_{{\rm{IM}}}}} \right| = \left| {{\mathit{\boldsymbol{\varDelta }}_{{\rm{Linearization}}}}} \right| + \left| {{\mathit{\boldsymbol{\varDelta }}_{{\rm{Reduction}}}}} \right| + \left| {{\mathit{\boldsymbol{\varDelta }}_{{\rm{Unmodeled}}}}} \right|$ |
为了实际计算的方便,通常用一阶不确定性带宽
| ${\mathit{\boldsymbol{\varDelta }}_u}(s) = \left[ {\begin{array}{*{20}{c}}{\displaystyle\frac{{0.7(s + 0.15)}}{{s{\rm{ + 0}}{\rm{.32}}}}} & 0 & 0\\0 & {\displaystyle\frac{{{\rm{0}}{\rm{.8(}}s{\rm{ + 0}}{\rm{.025)}}}}{{s{\rm{ + 0}}{\rm{.2}}}}} & 0\\0 & 0 & {\displaystyle\frac{{{\rm{0}}{\rm{.86(}}s{\rm{ + 0}}{\rm{.5)}}}}{{s{\rm{ + 1}}{\rm{.5}}}}}\end{array}} \right]$ |
鲁棒控制设计问题分为鲁棒稳定性问题和鲁棒性能问题[5]。鲁棒稳定性问题是指鲁棒控制器

|
图 5 鲁棒控制问题 |
图中向量u和向量y分别是系统
| $ \left\{ \begin{array}{l}\mathit{\boldsymbol{z}} = {P_{11}}\mathit{\boldsymbol{w}} + {P_{12}}\mathit{\boldsymbol{u}}\\\mathit{\boldsymbol{y}} = {P_{21}}\mathit{\boldsymbol{w}} + {P_{22}}\mathit{\boldsymbol{u}}\\\mathit{\boldsymbol{u}} = K(s)\mathit{\boldsymbol{y}}\end{array} \right.$ | (1) |
由式(1)可得
| $\left\{ \begin{array}{l}\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{T}}_{zw}}(s)\mathit{\boldsymbol{w}}\\{\mathit{\boldsymbol{T}}_{zw}} = {P_{11}} + {P_{12}}\mathit{\boldsymbol{K}}{(\mathit{\boldsymbol{I}} - {P_{22}}\mathit{\boldsymbol{K}})^{ - 1}}{P_{21}}\end{array} \right.$ |
由最小增益理论可知,如果控制器
| ${\mu _\Delta }({\mathit{\boldsymbol{T}}_{zw}}(s)) < 1$ |
式中:
所谓鲁棒性能就是控制系统在一定的参数(结构、大小)扰动情况下,仍能使系统保持特定的性态表现的能力。将表示对系统性能要求的虚拟不确定性量

|
图 6 鲁棒控制问题 |
以上鲁棒控制设计所采用的是D-K循环μ-综合算法[9],需要注意的是这种算法不是凸优化算法,所得的结果有时并不是收敛的,特别是在混合扰动下,计算所得的控制器参数也偏于保守,但在鲁棒控制设计问题中往往能达到较好的效果。
3.2 多变量鲁棒反馈控制器合成针对不确定性Canadian SCWR系统模型的鲁棒控制设计过程如下。
1)设立目标函数。设立目标函数的目的就是通过以下的鲁棒控制的设计过程完成对系统变量间的解耦,如此在鲁棒控制器设计完成后如果系统表现仍不能满足系统的性能要求,可通过局部调节以使系统达到较理想的性能要求。
2)构建系统闭环关联图的基本框架。根据系统模块和鲁棒控制模块之间的关系,建立模块如图7所示。初步设置权重函数。其中
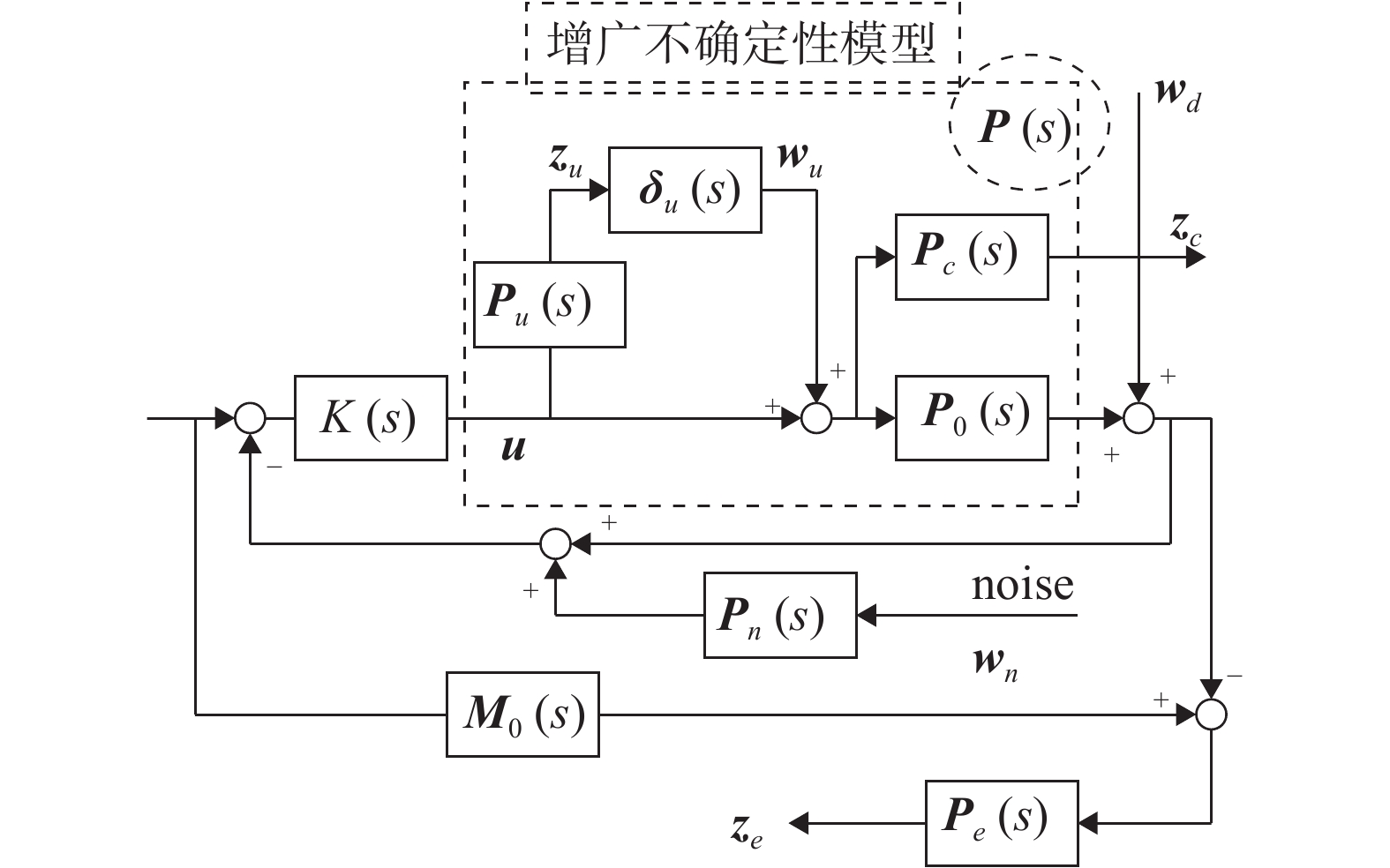
|
图 7 系统闭环关联图 |
3)选择性能权重函数。在2)的基础上,通过仿真结果分析,判断系统在初始权重函数的设置下所得的鲁棒控制器是否满足鲁棒性准则。如果系统未能达到稳定状况,变动模块图中的权重函数,直到系统能达到稳定状况为止。如果系统响应稳定,即满足
通过系统仿真得到稳定的鲁棒控制器
考虑到Canadian SCWR系统的动态特征[3],蒸汽温度和反应堆功率之间的耦合性较强,因而在鲁棒控制的基础上加入前馈控制部分以局部减弱温度和功率间的耦合程度,其结构如图8所示。
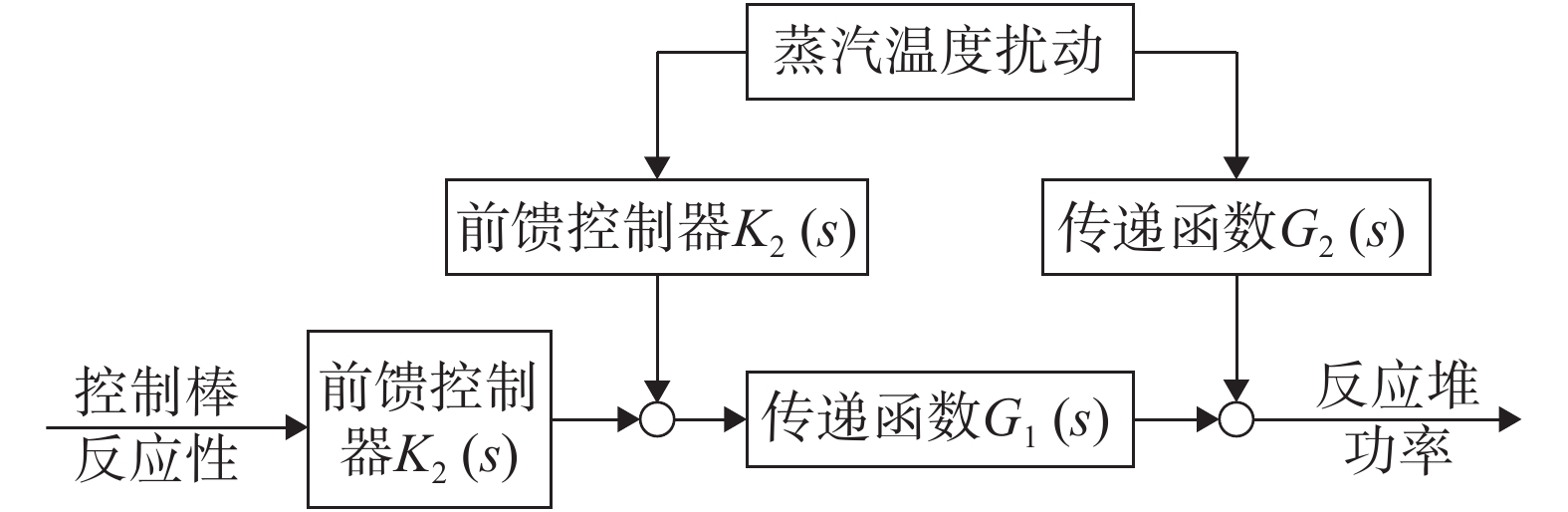
|
图 8 前馈控制器设计原理 |
图中函数
| ${G_2}(s) + {G_1}(s){K_2}(s) = 0$ | (2) |
最后,利用最小二乘法拟合式(2)所得的高阶函数得到一个一阶前馈控制器[10]。对于加入鲁棒控制器后系统反应堆功率响应对功率输入设置的追踪能力较弱的问题,可通过改变系统开环的增益值来改善,经过反复的仿真实验,调出反应堆功率和主蒸汽压力通道上的较优的开环增益。
5 仿真结果及分析把传统控制器、鲁棒反馈控制器和鲁棒前馈/反馈控制器分别加入系统模型后改变系统各输入,系统响应对比如图9~11所示。
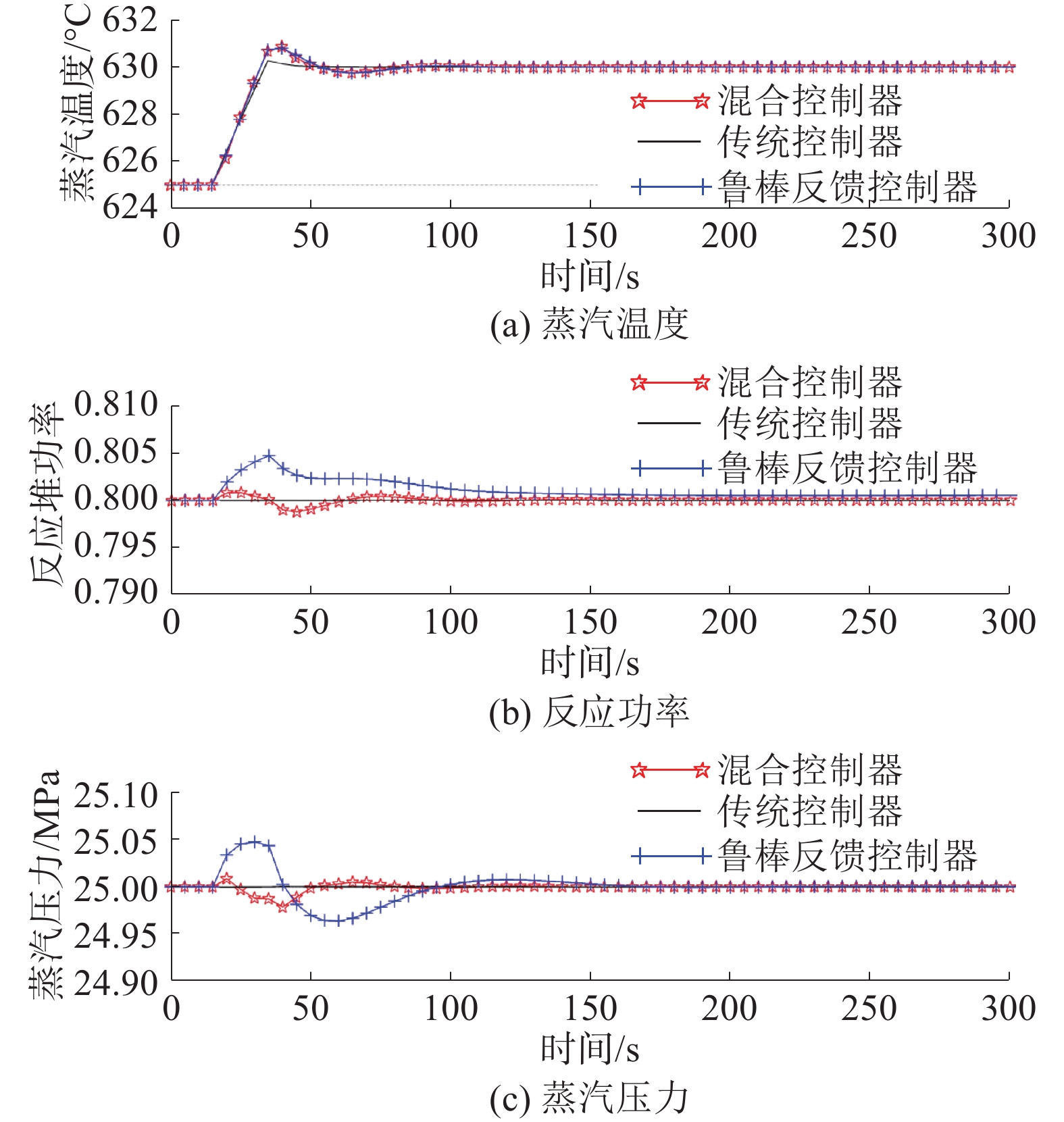
|
图 9 蒸汽温度从625 ℃斜坡变化到630 ℃时系统响应 |
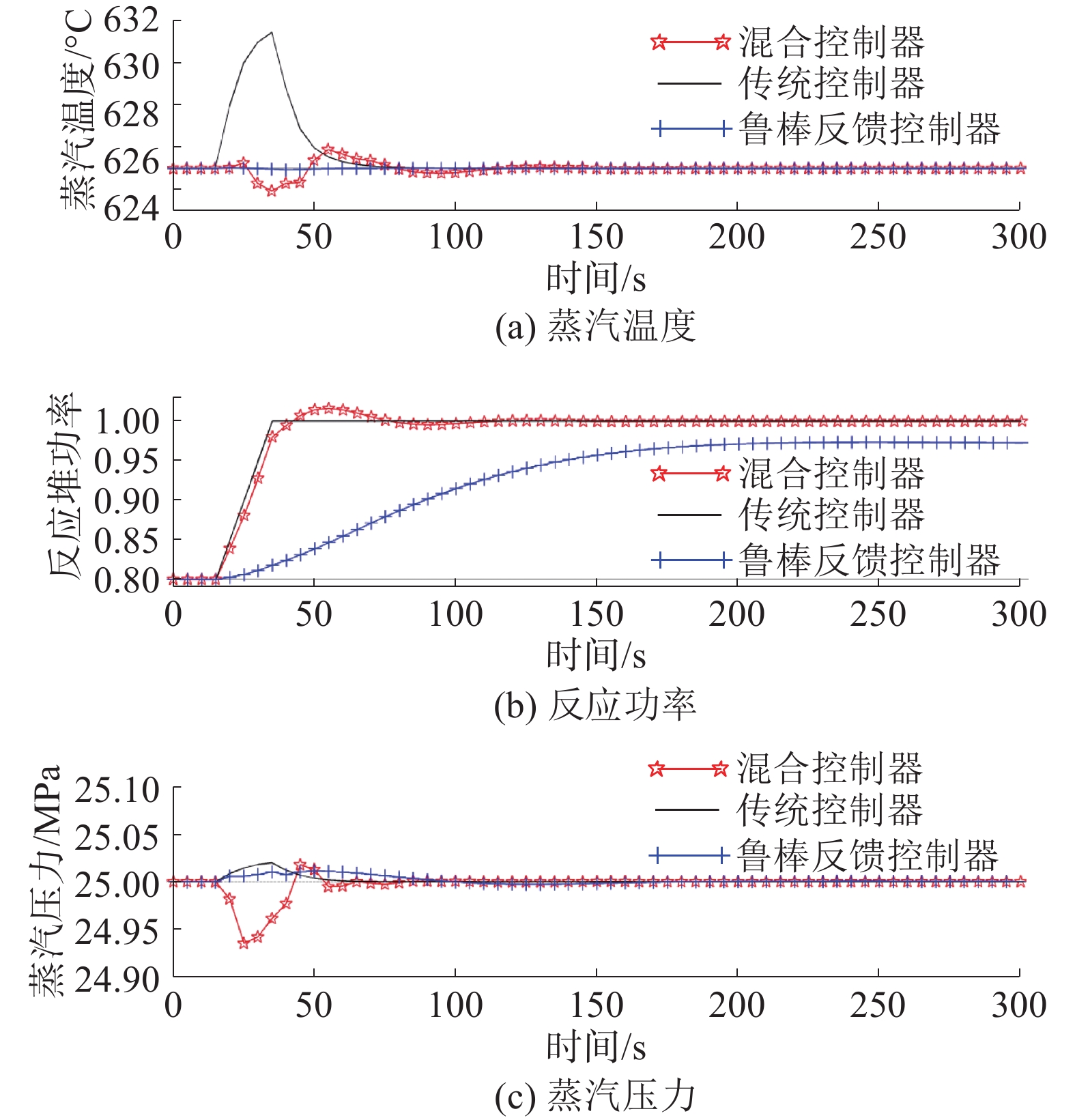
|
图 10 功率从80%斜坡变化到100%时系统响应 |
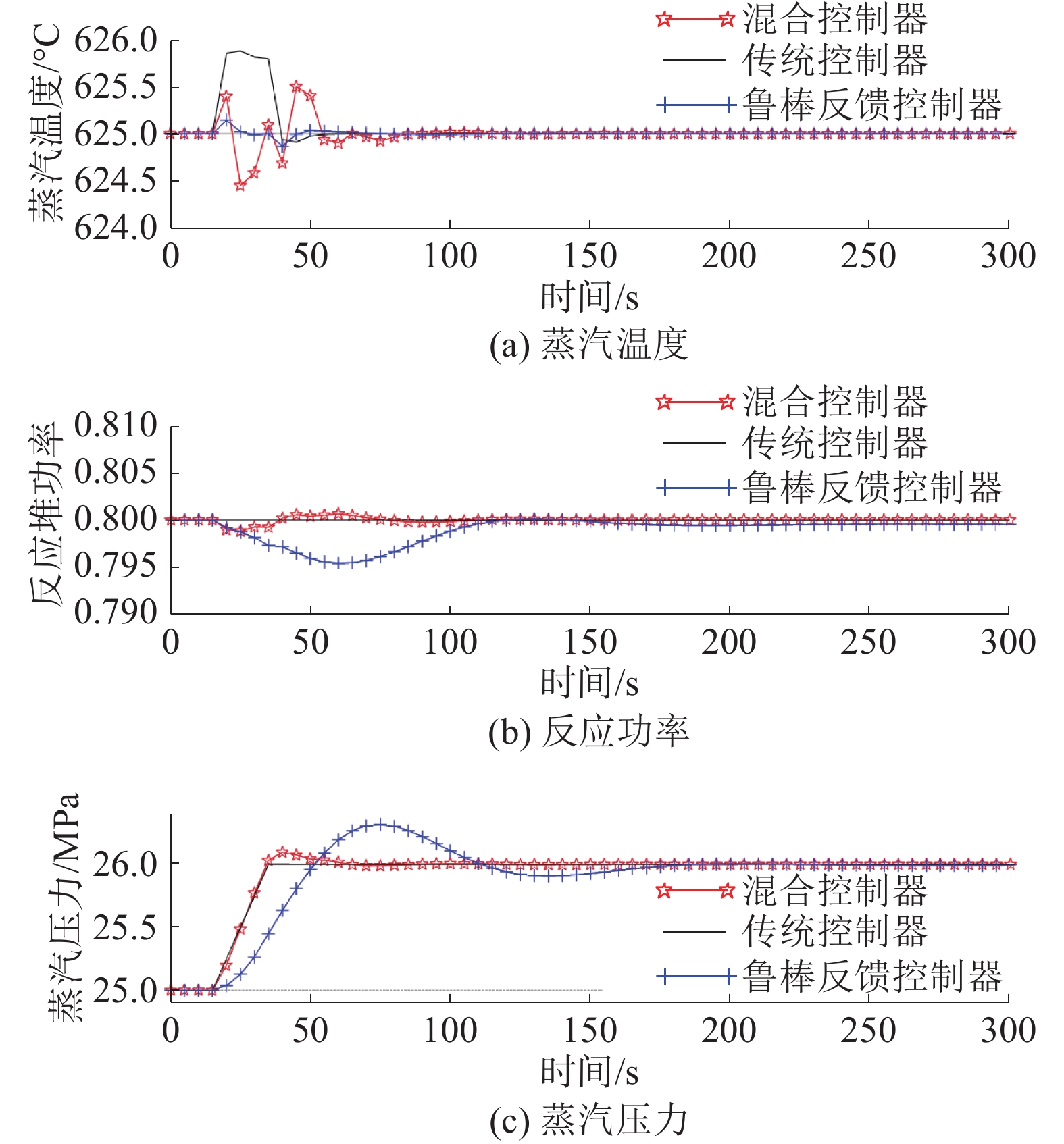
|
图 11 压力从25 MPa斜坡变化到26 MPa系统响应 |
当反应堆功率从80%逐渐提升至100%时,传统控制器所对应的蒸汽温度的响应跨度超过5 ℃,这是不被系统响应性态要求所允许的。另一方面,从图9~11可看出鲁棒控制器的诸多不足,如其所对应系统对反应堆功率的追踪能力较差,特别是对反应堆功率讯号的追踪;当主蒸汽压力设置从25 MPa变化到26 MPa时,系统主蒸汽压力响应的超调量偏大。而这两个方面反而是传统控制器表现更好。之所以产生这样的结果是因为Canadian SCWR系统的复杂程度、系统非线性度和模型函数的阶数都很高,这就导致在分别利用60%、80%和100%的系统功率状况下由于所选功率跨度大所求解的不确定性量也较大,另一方面,从模型函数的奈奎斯特图形和系统的动态模型稳定增益矩阵可以看出,系统变量之间的耦合性很强,所设计的鲁棒控制器无法在满足不确定性系统的稳定性后仍满足对系统的解耦要求。在鲁棒控制加入前馈控制部分后,系统响应有明显地改善,如图9~11中实线所示。所以,所设计的鲁棒前馈/反馈控制器能满足系统性能对控制系统设计的要求。
6 结论通过对Canadian SCWR系统模型进行不确定性分析,然后采用μ-合成方法得到多变量鲁棒控制器,最后通过前馈系统的扰动补偿特征和对开环系统的增益调整方法分析得到系统的前馈控制部分,将其加入到鲁棒反馈控制系统中来进一步提高系统的性能响应。通过和传统控制器的仿真结果作对比,得到以下结论:
1)通过对Canadian SCWR系统模型的不确定性分析,定量化系统未建模不确定性、模型线性化不确定性和模型简化不确定性,在此基础上进行的鲁棒控制系统设计更符合实际Canadian SCWR控制系统设计要求。
2)根据Canadian SCWR系统的动态特征,利用基于数据的最小二乘拟合法,采用局部解耦的策略设置前馈控制部分,进一步提升鲁棒控制器的性能。
3)针对Canadian SCWR系统模型所设计的多变量鲁棒前馈/反馈控制器能在系统不确定性条件下实现对系统的稳定控制,并使系统的响应特征满足所期待的设计要求,特别是它能较理想地控制蒸汽温度对反应堆功率变化的敏感性。
4)与传统控制器相比,多变量鲁棒前馈/反馈控制器能在较大的功率工况范围下实现对Canadian SCWR系统的有效控制,能更好地处理外界信号扰动、噪音及系统不确定性。
| [1] |
秋穗正, 苏光辉, 田文喜, 等. 先进核电厂结构与动力设备[M]. 北京: 中国原子能出版社, 2016: 155-165.
( 0) 0)
|
| [2] |
MACDONALD P, BUONGIORNO J, STERBENTZ J, et al. Feasibility study of supercritical light water cooled reactors for electric power production[EB/OL]. [2016-11-23]. http://xueshu.baidu.com/s?wd=paperuri%3A%2859502750251b87c45476b90cbdfab54b%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fdigital.library.unt.edu%2Fark%3A%2F67531%2Fmetadc786150%2Fm1%2F&ie=utf-8&sc_us=13490827312544854618.
( 0) 0)
|
| [3] |
SUN P. Dynamic model construction and control system design for Canadian supercritical water-cooled reactors[EB/OL]. [2016-12-10]. http://works.bepress.com/peiwei_sun/1/.
( 0) 0)
|
| [4] |
WEINMANN U A. Uncertain models and robust control[M]. Vienna: Springer, 1991: 31-38.
( 0) 0)
|
| [5] |
GU D W, PETKOV P H, KONSTANTINOV M M. Robust control design with MATLAB® (Advanced Textbooks in Control & Signal Processing)[M]. London: Springer, 2005.
( 0) 0)
|
| [6] |
段广仁. 线性系统理论[M]. 哈尔滨: 哈尔滨工业大学出版社, 2003: 352-360.
( 0) 0)
|
| [7] |
BALAS G, CHIANG R Y, SAFONOV M G. Robust Control ToolboxTM 3 User's Guide[EB/OL]. [2016-10-13]. http://se.mathworks.com/help/pdf_doc/robust/robust_ug.pdf.
( 0) 0)
|
| [8] |
DOYLE J C, GLOVER K, KHARGONEKAR P P, et al. State-space solutions to standard H2 and H∞ control problems
[J]. IEEE transactions on automatic control, 2002, 34(8): 831-847. ( 0) 0)
|
| [9] |
LIN J L. Control system design for robust stability and robust performance[EB/OL]. [2016-10-10]. https://lra.le.ac.uk/handle/2381/34797.
( 0) 0)
|
| [10] |
孙晓芳. 基于有理函数的数据拟合方法[J]. 电脑信息与技术, 2005, 13(3): 8-9. ( 0) 0)
|
 2017, Vol. 44
2017, Vol. 44


